GNSS信号捕获中的伪码多普勒补偿技术

黄新明，龚航，朱祥维，欧钢



GNSS信号捕获中的伪码多普勒补偿技术

黄新明，龚航，朱祥维，欧钢

(国防科技大学电子科学与工程学院，湖南长沙，410073)

针对全球导航卫星系统(GNSS)信号捕获中存在伪码多普勒，提出一种基于时延控制的伪码多普勒补偿方法，通过数字延迟滤波器补偿由于伪码多普勒引入的本地码和接收信号的相位不匹配。给出包括码多普勒补偿在内的新的GNSS信号捕获结构，并对全球定位系统(GPS)C/A码信号进行仿真验证。研究结果表明：延迟滤波器阶数越大，码多普勒的补偿效果越好；在采样率为5 MHz时，采用三阶Farrow结构的分数阶延迟滤波器捕获损耗降低至0.2 dB。

全球导航卫星系统；伪码多普勒补偿；时延控制；可变分数阶延迟滤波器

卫星和用户之间的相对运动、接收机晶振的老化等都会使得接收到的信号含有多普勒，包括载波多普勒和码多普勒[1]。在一般情况下，码多普勒较小，只有载波多普勒的几百甚至几千分之一，因此，在常规的接收机捕获时通常不考虑信号的码多普勒带来的影响[2−3]。但是对于高灵敏度接收机不得不考虑码多普勒的影响，特别是当用户动态较高时，码多普勒成为了一个捕获不得不考虑的因素。高灵敏度接收机需要较长的积累来获得足够的载噪比，但是由于存在码多普勒，本地码和接收信号之间会出现严重的不匹配。在极端情况下，当伪码多普勒频移所造成的码片之间的不匹配超过半个码片时，增长相干积累时间不仅不会提高增益，反而会降低整个信号的捕获性能，因此，需要对码多普勒进行补偿。码多普勒对信号捕获的影响体现在接收信号和本地生成信号不一致导致的码相关峰值损耗上。如果要补偿码多普勒的影响，就需要消除接收机和卫星的码速率之间的不一致现象。一种码多普勒补偿的直观方式就是根据载波和伪码的比例关系，利用载波辅助伪码，在改变载波多普勒搜索步进的同时也实时改变本地伪码生成速率，当载波多普勒完成搜索时，伪码多普勒也实现了补偿。然而，对于在GNSS信号快速捕获中广泛应用的基于快速傅里叶变换(FFT)的信号捕获结构[2]，这种码多普勒补偿方法将使得其实现难度加大。因为改变本地生成码的生成频率就意味着本地码进行FFT变换的点数一直在变。同样，这种补偿方法也不适用于基于匹配滤波器的并行捕获结构[4]，这是因为本地码生成频率的持续变化致使匹配滤波器的系数需要不断刷新，这将导致实现结构复杂以及处理时间增加。因此，通过改变本地码生成频率实现多普勒补偿对捕获时间要求很高的高灵敏度导航信号捕获来说并不是个很好的解决方案[5]。本文作者提出一种基于时延控制的伪码多普勒补偿方法，通过实时调整接收信号延迟完成码多普勒的补偿，可以不需要改变本地码的生成频率。通过损耗评估补偿前后码多普勒对信号捕获的影响。同时，也给出了该方法的实现结构，并进行了相应的仿真分析。

1 伪码多普勒的影响分析

导航接收机常规的捕获结构如图1所示[1]，经过ADC采样后的中频信号可以表示为

图1 常规导航信号的捕获结构图

Fig. 1 Scheme of conventional GNSS signal acquisition structure

其中：为信号的幅度；()为导航电文数据；()为扩频码；IF为中频频率；D为多普勒频率；s为系统采样周期；()为噪声项，其方差为。

在不计噪声的情况下，经过相关积分非相干后积累输出的检测量值为

其中：nc为后积累次数；d为残留多普勒频率；coh为相关积分时长；为以码片宽度c为单位的码相位延迟；(∙)为码的自相关函数；()为噪声项。可以看出，捕获性能与载波多普勒以及伪码相位误差有关。相关积分后的积累值()与()中的噪声均服从正态分布[1]，故(2)式给出的非相干积累后的检测量服从自由度为2nc的卡方分布。

设给定的信号捕获虚警率为FA，则相应的捕获门限值可以由下式确定：

对应的检测概率为

其中：为非中心参量，可用归一化均值和自由度定义，为。

上面给出了常规导航信号的捕获结构及其捕获性能，下面分析伪码多普勒对捕获性能的影响。

接收机的信号捕获过程一般是通过对某颗卫星信号的载波频率和码相位这二维进行扫描式搜索来完成的。通常并没有考虑码多普勒的影响，这在常规情况下是可以的，因为一般情况下码多普勒比较小，而且总的积分时间较短，码多普勒引起的码相位的误差不是很大，对式(2)中的统计检测量的影响较小。但是如果接收信号比较弱，会导致需要较长的积分时间，这时码多普勒的影响就不能忽略。为了直观评价码多普勒对捕获性能的影响，参考文献[6]，分析不同积分时间下伪码峰值损耗，峰值损耗定义为

其中：()为存在码多普勒条件下的相关峰值；0()为无码多普勒条件下的相关峰值。

存在码多普勒条件下的捕获性能同样可由(3)及(4)式确定，不同的是其中的非中心参量为

采用GPS C/A码进行仿真验证，其码率为1.023 Mcps，采样速率为5 MHz，仿真采用具有普遍意义的相干积分加非相干后积累的方式的捕获结构，分析总的积分时间与伪码峰值损耗的关系，仿真结果如图2所示。不失一般性，选取相关积分时间为20ms，码多普勒取5Hz。从图2可以看出：随着总积分时间的增大，伪码多普勒引入的峰值损耗越明显，当总积分时间将近1 s时，伪码峰值损耗高达11 dB，这样的损耗对于导航信号捕获来说是无法容忍的，需要对码多普勒进行补偿。

图2 不同积分时间下的伪码峰值损耗

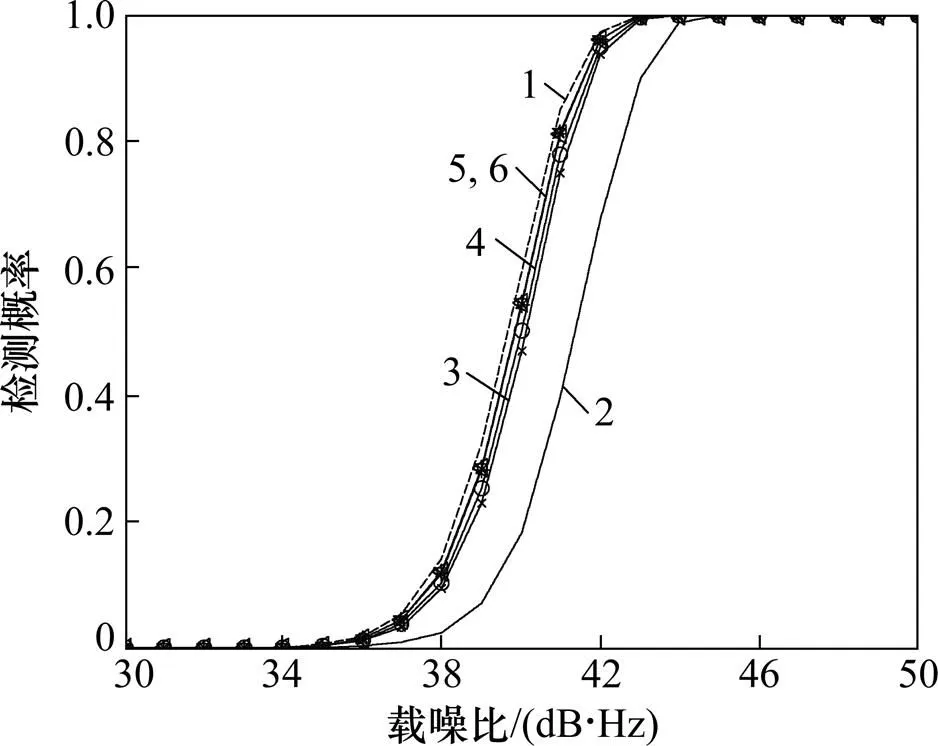
图3给出了总积分时间为100 ms时存在伪码多普勒和没有伪码多普勒的捕获性能对比，可见存在伪码多普勒时检测性能出现了较明显下降。

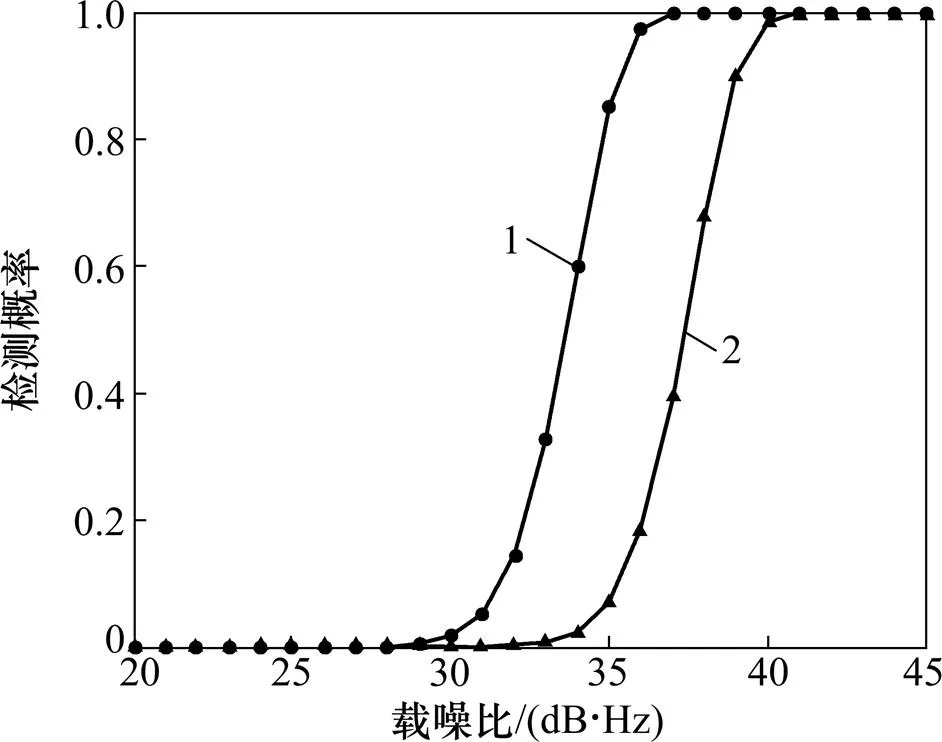
1—无伪码多普勒；2—存在伪码多普革

2 基于时延补偿的伪码多普勒补偿方法

根据采用的方法不同，伪码多普勒的补偿策略不同。若捕获时采用的是长相干积累的方法，则需要在相干积累前完成伪码多普勒的补偿；若采用的是相干积累加非相干后积累的方式，前面的相干积分时间较短，引入的损耗较小，则可以在积分后进行伪码多普勒的补偿，以节省硬件资源。总体来说，2种方法的基本原理相同，不同之处在于伪码多普勒补偿的位置不同。也可以在2个位置均保持伪码多普勒补偿，这样补偿效果更加精细，当然导致硬件资源增大。

2.1 实现原理

在GNSS接收机中，通过伪码数控振荡器(NCO)生成的本地伪码信号可以表示如下：

其中：c为生成伪码信号的周期；为本地伪码信号生成周期；()为对应卫星的码片波形；c为对应卫星伪码序列的第个元素。

为了充分讨论码多普勒的补偿方法，这里假设经过下变频及载波剥离后的接收信号没有残余的载波多普勒，功率也进行归一化，可以表示如下：

其中：s为采样频率；d为码多普勒频率。

由于多普勒的影响，接收到的信号会出现信号周期的伸张压缩，即接收信号的周期会变大或变小。当积分时间较长时，本来对齐的伪码相位就会不再对齐，这样就会影响信号的积累增益。特别是当本地伪码和接收信号的伪码滑动超过半个伪码周期时，继续增加积分时间将无益于捕获性能的提升，反而会降低捕获性能。这是因为伪码相位误差超过半个码片后积累的信号功率没有积累的噪声功率强。为了避免码多普勒带来的不良影响，一种直观的解决途径就是使得接收到的信号的伪码和本地生成的伪码在所有的采样点都保持对齐，即()d()，因此，接收机的采样周期和本地伪码的生成信号的周期需要满足下式：

为了保证本地伪码频率的恒定，根据式(9)，接收机的采样频率需要随着多普勒的调整而调整才能满足式(9)。然而，接收机的A/D转换器通常没有能力实时改变信号的采样率，即所接收的信号的采样率是恒定的，因此，改变采样频率的方法也不可取，本文提出了一种通过数字滤波器完成多普勒补偿的方法，不需要改变采样频率。根据式(8)，所接收的信号也可以表示为

基于上述原理，本文作者提出了一种基于数字时延控制的码多普勒补偿方法，并给出了包括码多普勒补偿在内的新的GNSS信号捕获结构如图4所示。新的GNSS信号捕获结构包括3个部分，即载体剥离、伪码多普勒补偿和相干积累。其中载体剥离和相干积累等操作和传统的捕获结构实现方法相同。码多普勒补偿是通过时延控制实现，包括整数采样点的延迟和分数阶延迟。整数采样点延迟采用先入先出(FIFO)结构的存储器即可实现，而分数阶延迟采用FARROW结构的分数阶延迟滤波器实现。可变分数阶延迟滤波器的设计实现可以参考文献[7−19]中提出的方法。下面设计所需的可变分数阶延迟滤波器。

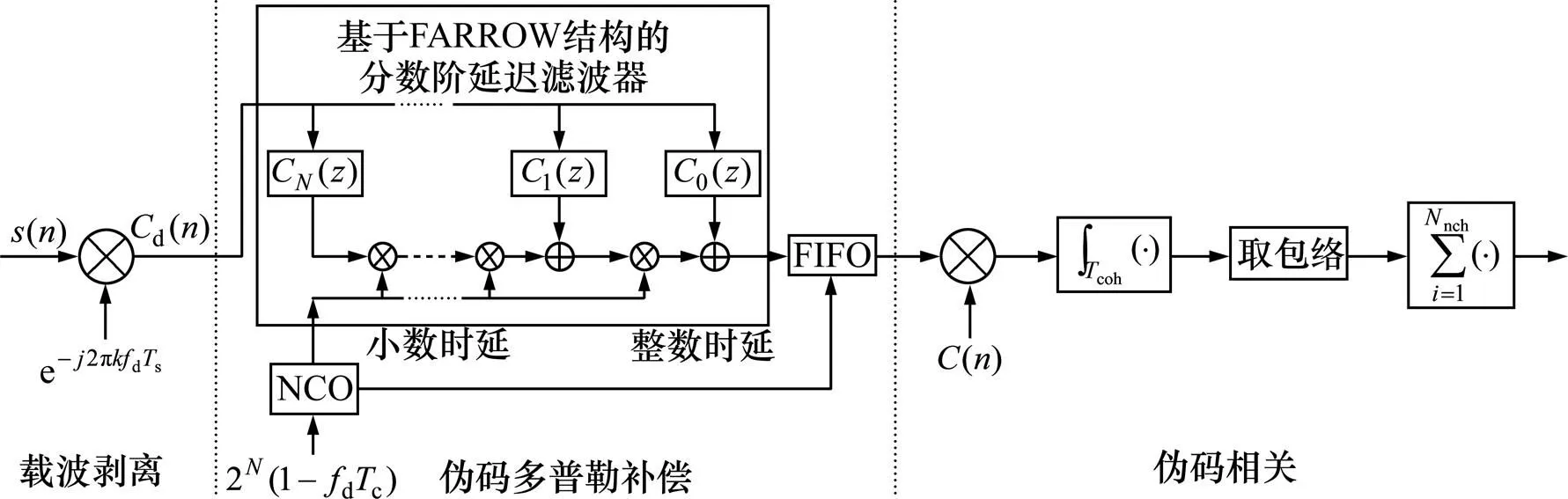
图4 具有码多普勒补偿模块的GNSS信号捕获结构

基于时延控制的码多普勒补偿方法需要实时获取时延补偿值，用于补偿不匹配的整数采样点延迟和小数采样点延迟。提出利用NCO的方式获取采样点间的不匹配延迟，其实现结构与常规NCO的一致，具体实现见文献[1]，这里仅给出其设计指标。由图4可以看出：NCO输入的累加控制字为(其中，为NCO的累加位数)。累加的溢出值用于控制整数采样点延迟，未溢出累加值用于控制小数采样点延迟。其中，码多普勒的值根据载波和伪码的比例关系来确定，延迟补偿的分辨率为。

2.2 可变分数阶延迟滤波器的设计

可变分数阶延迟滤波器采用FARROW结构的分数阶延迟滤波器实现。文献[7−19]给出了可变分数阶延迟滤波器的设计实现方法，一般流程是根据给出的幅频以及相频特性指标求解滤波器系数以及阶数，是一个非线性的优化问题，求解难度较大。下面先介绍FARROW结构延迟滤波器的基本实现结构，然后给出一种简单可行的设计方案。

FARROW结构的可变延迟滤波器基本原理是采用多项式拟合滤波器系数，设滤波器系数可以表示为

滤波器传输函数如下：

(12)

其中：为子滤波器的阶数；为多项式阶数，该结构示意图如图5所示。从图5可以看出：该结构只需要更新时延值就可以实现可变时延的控制。

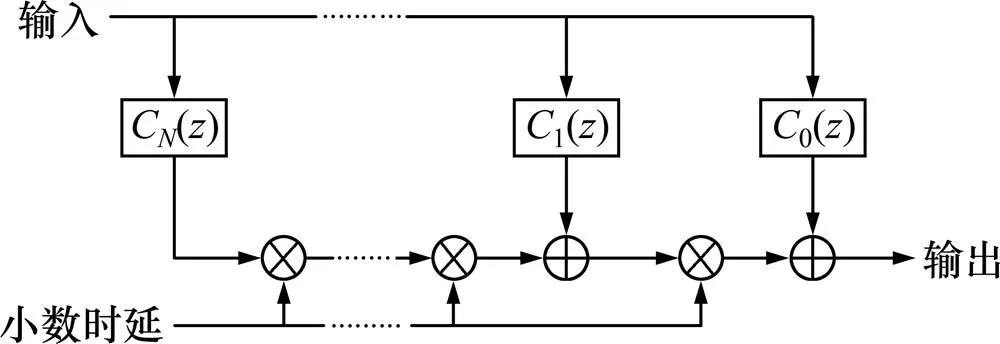
图5 基于FARROW结构的可变分数阶延迟滤波器的实现结构

为了简化FARROW结构分数阶延迟滤波器的设计，这里给出一种简单可行的设计方案。其基本原理是利用迭代的方法，不断迭代子滤波阶数以及多项式的阶数，直到指标满足要求为止。其基本实现步骤如下：

1)首先利用广义最小二乘法设计一组固定时延的分数阶延迟滤波器[7]，阶数为，指标高于所需滤波器的要求，时延范围为0~1个采样点，步进根据所需达到的精度确定。

2)利用1个阶多项式拟合逼近得到的这组滤波器的系数，可以得到组阶多项式的系数，这些系数构成了1个FARROW结构延迟滤波器。

3)考察得到的可变分数阶延迟滤波器的性能指标是否达标，若达标则设计完成，若不达标则增加阶数和多项式阶数，从步骤1)开始重新迭代设计，直到设计的滤波器满足所需指标为止。

采用给出的方法设计所需的可变分数阶延迟滤波器，信号采样频率为5 MHz，信号带宽为±1.023 MHz，时延精度为0.01个采样点，带内最大幅度波动为0.1 dB，设计得到的三阶FARROW结构的可变延迟滤波器的幅频特性和相频特性如图6和图7所示。

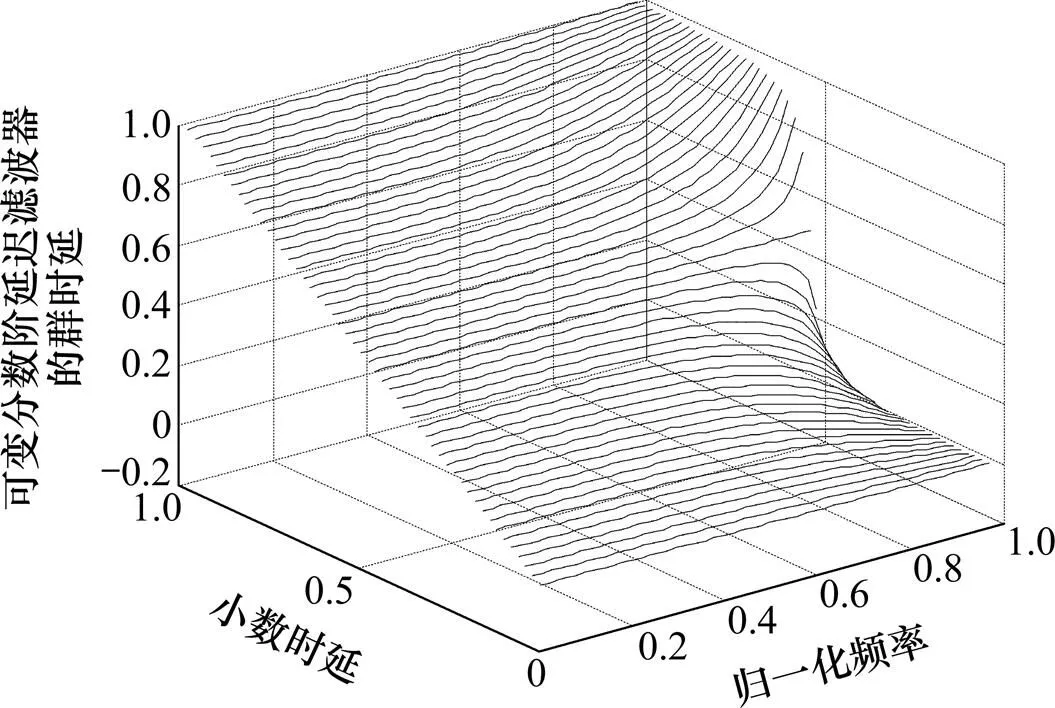
图6 可变分数阶群时延响应特性

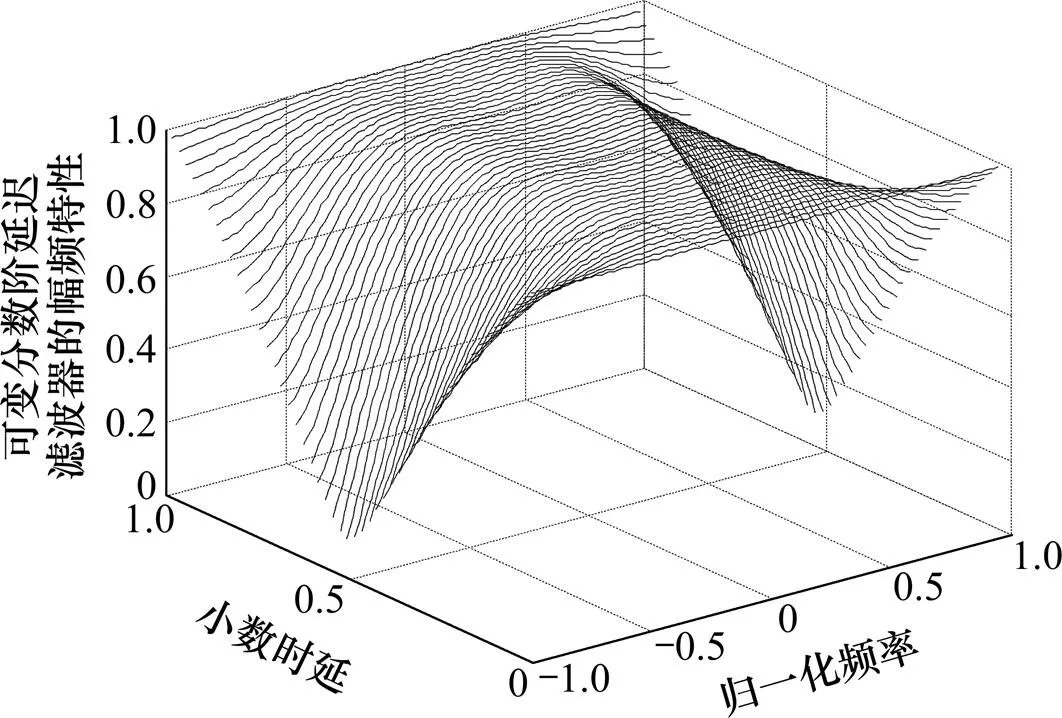
图7 幅频响应特性

从图6和图7可以看出：设计出来的可变分数阶延迟滤波器的幅频响应以及群时延精度在通带范围内满足所需要求。

2.3 补偿误差分析

在不计噪声的情况下，经过上述多普勒补偿以及相关积分后的输出为[10]

其中：()为阶滤波器的幅频响应；为阶滤波器的相频响应；为滤波器固定群延迟；c为伪码速率。对应的频率响应函数为

理想情况下的相关积分输出为

对应的频率响应函数为

则分数阶延迟滤波器的补偿误差如下：

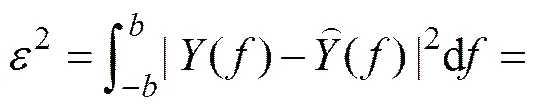
式(17)为由于分数阶延迟滤波器引入的补偿误差，可以作为分数阶延迟滤波器设计的一个约束指标。

对应加有伪码多普勒补偿模块的捕获方法的捕获性能仍然能够按照式(3)与(4)评估，其中，非中心参量需要更正为下式：

3 数值仿真

为了评估本文提出的码多普勒补偿方法，对GPS信号进行仿真验证，其信号捕获的实现结构如图4所示。分别对高动态和弱信号两种条件下的伪码多普勒补偿性能进行仿真验证。这里需要特别说明的是：为了简便分析，本文的高动态条件均指一阶动态。采用GPS C/A码进行仿真验证，其码率为1.023 Mcps，采样速率为5 MHz。仿真采用具有普遍意义的相关积分加非相干后积累的方式的捕获结构。

3.1 高动态条件下的损耗分析

下面对存在码多普勒补偿和无码多普勒补偿2种情况下的捕获性能进行了仿真验证，其中相关积分时间为5 ms，非相干后积累次数为10次，则总的积分时间为50 ms，仿真结果如图8~10所示。这里同样采用伪码峰值损耗以及恒虚警概率下的检测概率来评估码多普勒对捕获性能的影响。由图8可见：当码多普勒超过33 Hz时，引入的捕获损耗超过了6 dB。

图8 不同码多普勒条件下的伪码峰值损耗

从图9和图10可以看出：本文提出的基于时延控制的伪码多普勒补偿方法是一种有效减小伪码多普勒影响的解决方案。采用常数插值滤波的方式，即文献[5]给出的码多普勒补偿方式，峰值损耗可以降低至0.5 dB以下，捕获性能有了明显改善。随着滤波器阶数的增大，由码多普勒造成的峰值损耗就越小，捕获性能改善得越明显。当采用三阶FARROW结构分数阶延迟滤波器时，峰值损耗可降低至0.2 dB左右。若再提高滤波器阶数，则峰值损耗降低很小。所以，在实际应用中取3阶延迟滤波器是比较好的一个选择。

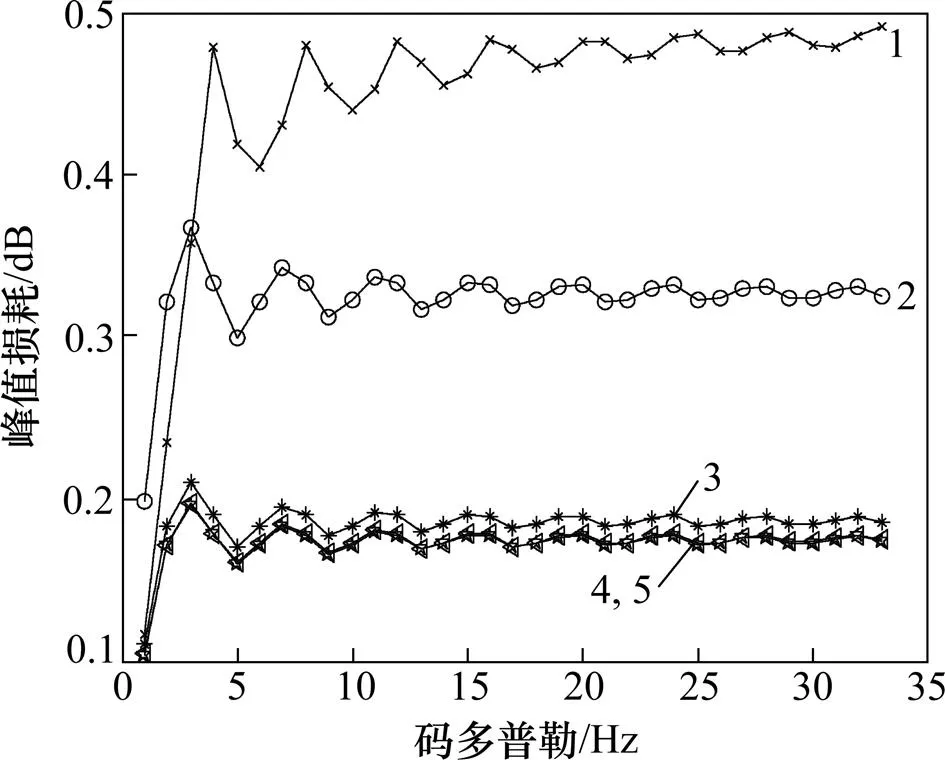
1—常数插值滤波器；2—一阶滤波器；3—三阶滤波器；4—五阶滤波器；5—七阶滤波器；

1—无伪码多普勒；2—存在伪码多普勒；3—常数插值补偿；4—一阶滤波器补偿；5—三阶滤波器补偿；6—五阶滤波器补偿；7—七阶滤波器补偿

3.2 弱信号条件下的损耗分析

与高动态条件下一样，下面对弱信号条件下存在码多普勒补偿和无码多普勒补偿2种情况下的捕获性能进行仿真验证，其中取相关积分时间为20 ms，码多普勒频率为5 Hz，分析伪码峰值损耗随总积分时间的变化关系，仿真结果如图2和图9所示。这里同样采用伪码峰值损耗以及恒虚警概率下的检测概率来评估码多普勒对捕获性能的影响。从仿真结果可以看出：随着中频积累时间的增大，由码多普勒引入的峰值损耗越明显，当总积分时间将近1 s时，伪码峰值损耗高达11 dB。

图11所示为进行码多普勒补偿后的伪码峰值损耗随中频积累时间的关系。从图11可以看出：本文提出的基于时延控制的码多普勒补偿方法是一种有效减小弱信号条件下码多普勒影响的解决方案。采用常数插值滤波的方式峰值损耗和高动态条件下一样可以降低至0.5 dB以下。并且随着滤波器阶数的增大，由码多普勒造成的峰值损耗就越小，当采用三阶FARROW结构分数阶延迟滤波器时，峰值损耗同样可降低至0.2 dB左右。

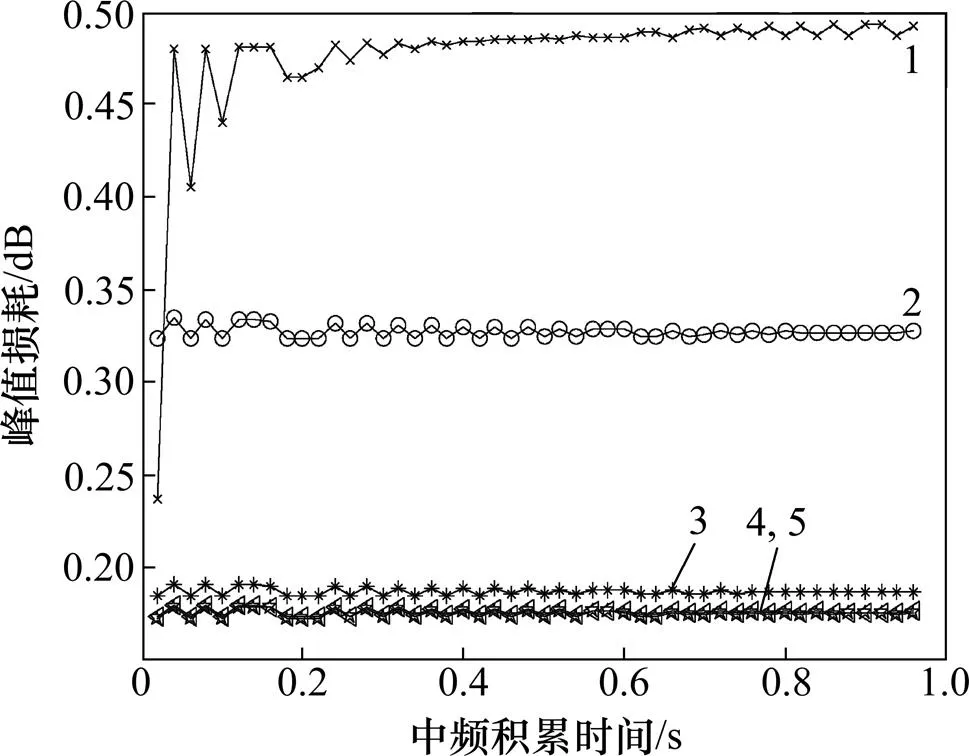
1—常数插值滤波器；2—一阶滤波器；3—三阶滤波器；4—五阶滤波器；5—七阶滤波器

图12所示为总积分时间为100 ms时进行码多普勒补偿后的捕获性能。将图12与图3对比可以看出：进行伪码多普勒补偿后，检测性能得到了较明显提升。

1—无伪码多普勒；2—存在伪码多普勒；3—常数插值补偿；4—一阶滤波器补偿；5—三阶滤波器补偿；6—五阶滤波器补偿；7—七阶滤波器补偿

4 结论

1) 在一阶动态及弱信号条件下，采用相关积分−非相干后积累的捕获方式对GPS C/A码进行仿真验证。在一阶动态条件下，相关积分时间为5 ms，非相干后积累次数为10次，未进行伪码多普勒补偿条件下，码多普勒达到33 Hz时引入的捕获损耗为6 dB。在弱信号条件下，相关积分时间为20 ms，码多普勒频率为5 Hz，未进行伪码多普勒补偿条件下，当总积分时间将近1 s时，伪码峰值损耗为11 dB。

2) 利用本文提出的方法对2种条件下的伪码多普勒进行补偿。采用常数插值滤波的方法时，峰值损耗降低至0.5 dB左右；采用三阶FARROW结构分数阶延迟滤波器时，峰值损耗降低至0.2 dB左右。随着滤波器阶数的增大，由码多普勒造成的峰值损耗越小，捕获性能改善越明显。

[1] Kaplan E D, Hegarty C J. Understanding GPS: Principles and applications[M].2nd ed. Boston: Artech House Inc, 2006: 58−61.

[2] James BY. Tsui Fundamentals of global positioning system receivers: A software approach[M]. New York: John Wiley & Sons, Inc, 2000: 137−138.

[3] Akopain D. Fast FFT based GPS satellite acquisition method[J]. IEE Proc.-Radar Sonar Navigation, 2005, 154: 277−286.

[4] Dafesh P A, Holmes J K. Practical and theoretical tradeoffs of active parallel correlator and passive matched filter acquisition implementations[C]//Proc IAIN World Congress, ION 56th Annual Meeting. San Diego, USA, 2000: 352−362.

[5] 黄仰博. 高性能导航接收机基带处理算法与实现技术研究[D]. 长沙: 国防科学技术大学电子科学与工程学院, 2011: 46−52. HUANGYangbo. Baseband algorithms and implementation tech. for high-performance navigation receiver[D]. Changsha: National University of Defense Technology. Department of Electronic Science and Engineering, 2011: 46−52.

[6] 李春霞. 高动态条件下伪码相关特性及其应用研究[D]. 长沙: 国防科学技术大学, 2005: 37−41.LI Chunxia. The characteristics of PN code correlation and its applications under high dynamics[D]. Changsha: National University of Defense Technology, 2005: 37−41.

[7] Laakso T I, Välimäki V, Karjalainen M, et al. Splitting the unit delay: Tools for fractional delay filter design[J]. IEEE Signal Processing Mag, 1996, 13(1): 30−60.

[8] Olkkonen J T, Olkkonen H. Fractional delay filter based on theB-Spline transform[J]. IEEE Signal Process. Lett., 2007, 14(2): 97–100.

[9] Shyu J J, Pei S C. A generalized approach to the design of variable fractional delay FIR digital filters[J]. Signal Process, 2008, 88(6): 1428−1435.

[10] Pei S C, Lin H S. Tunable FIR and IIR fractional-delay filter design and structure based on complex cepstrum[J]. IEEE Trans CircuitsSyst I, 2009, 56(10): 2195–2206.

[11] Tseng C C, Lee S L. Design of fractional delay filter using weighted hermite interpolation method[J]. IEEE Trans Circuits Syst I, Reg Papers, 2012, 59(7): 1458−1471.

[12] Selva J. An efficient structure for the design of variable fractional delay filters based on the windowing method[J]. IEEE Trans SignalProcessing, 2008, 56(8): 3770–3775.

[13] YA Junyu, XEI Jingxu. Mixed-radix fast filter bank approach for the design of variable digital filters with simultaneously tunable band-edge and fractional delay[J]. IEEE Trans Signal Processing, 2012, 60(1): 100–111.

[14] Tseng C C, Lee S L. Efficient design and implementation ofvariable fractional delay filters using differentiators[J]. IEEE Trans CircuitsSyst I: Reg Papers, 2011, 58(6): 1311–1322.

[15] Deng T B, Chivapreecha S, Dejhan K. Bi-minimax design of evenordervariable fractional-delay FIR digital filters[J]. IEEE Trans CircuitsSyst I: Reg Papers, 2012, 59(8): 1766–1774.

[16] Deng T B. Decoupling minimax design of low-complexity variable fractional-delay FIR digital filters[J]. IEEE Trans Circuits Syst I: RegPapers. 2011, 58(10): 2398–2408.

[17] Deng T B. Minimax design of low-complexity even-order variablefractional-delay filters using second-order cone programming[J]. IEEETrans Circuits Syst II: Exp Briefs, 2011, 58(10): 692−696.

[18] Deng T B. Hybrid structures for low-complexity variablefractionaldelay FIR filter[J]. IEEE Trans Circuits Syst I: Reg Papers, 2010, 57(4): 897−910.

[19] Shyu J J, Pei S C, Chan C H, et al. A new criterion for the design of variable fractional-delay FIR digital filters[J]. IEEE Trans Circuits Syst. I: Reg Papers, 2010, 57(2): 368–377.

[20] 许晓勇. 卫星导航接收机高精度建模、分析及优化设计研究[D]. 长沙: 国防科学技术大学电子科学与工程学院, 2008: 76−80.XUXiaoyong. Study on high-precision modeling, analysis and optimization design for satellite navigation receiver[D]. Changsha: National University of Defense Technology. Department of Electronic Science and Engineering, 2008: 76−80.

(编辑 陈爱华)

Code Doppler compensation method for GNSS signal acquisition

HUANG Xinming, GONG Hang, ZHU Xiangwei, OU Gang

(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

A code Doppler compensation method based on delay control was proposed to remove the influence of loss in acquisition performance because of code Doppler during global navigation satellite systems (GNSS) signal acquisition. Compensation of code Doppler was achieved by compensating the phase difference between the received and local signals with a digital delay filter. A new GNSS signal acquisition structure, including code Doppler compensation processing, was provided. Performance of the compensation method was analyzed and verified by simulation. The results show that the higher the order of the digital delay filter, the better the compensation performance. Moreover, detection loss can be reduced to less than 0.2dB with a 3th-order fractional delay filter realized by FARROW structure.

global navigation satellite system (GNSS); code Doppler compensation; delay control; variable fractional delay filter

10.11817/j.issn.1672-7207.2015.06.022

TF803.21

A

1672−7207(2015)06−2134−08

2014−06−13；

2014−08−20

国家自然科学基金资助项目(61403413)(Project (61403413) supported by the National Natural Science Foundation of China)

朱祥维，副研究员，从事卫星导航系统及时间同步技术研究；E-mail：zhuxiangwei@nudt.edu.cn