基于GARCH族模型的葡萄酒投资指数的波动性分析

胡景焕

[摘 要]对葡萄酒投资市场的波动性进行研究，选取伦敦葡萄酒交易所（LIV-EX）发布的样本区间为1988年1月至2013年11月的LIV-EX Fine Wine Investables Index月度数据，对FWI月收益率序列的平稳性、异方差性进行分析和检验。基于GARCH（广义自回归条件异方差，Generalized Auto-Regressive Conditional Heteroskedasticity）族模型来描述FWI的波动集聚性、敏感性及其杠杆效应。结果表明，FWI月收益率序列是平稳的，其指数波动具有高阶ARCH效应，并且具有正向非对称的反杠杆效应，但不存在ARCH in Mean效应。

[关键词]葡萄酒投资指数；收益率；GARCH族模型；波动性；杠杆效应

[中图分类号]F830.59 [文献标识码]A [文章编号]1671-8372（2015）03-0050-07

Study on the volatility of fine wine investable index based on GARCH family models

HU Jing-huan

（College of Transport and Communication， Shanghai Maritime University， Shanghai 201306， China）

Abstract：The monthly data of LIV-EX fine wine investable index（FWI）from Jan. 1988 to Nov. 2013 published by LIV-EX are selected in order to study the volatility of fine wine investment market and the stability as well as heteroskedasticity of its return series are analyzed and inspected. Then the volatility clustering， sensitivity and asymmetry of FWI are studied based on GARCH family models. Results show the return series of FWI is proved to be stable and there are high-level ARCH and anti-leverage effect on the fluctuation of fine wine， but there is no ARCH in mean effect.

Key words：fine wine investable index； rate of return； GARCH family models； volatility； leverage effect

改革开放以来，我国经济快速发展，GDP连续多年保持两位数的高增长，即使近几年受经济危机的影响增速略有回落，但仍然保持着适度的增长，人民的收入水平也有了很大提高。随着富裕程度的不断提高，人们也越来越关注储蓄之外的其他个人投资渠道。总的来看，当前我国个人投资的主要领域有房地产、贵金属、各类有价证券等。然而房地产的资金压力大、贵金属的不易变现及证券产品的高风险使得人们逐步将眼光扩展到其他投资渠道。在这其中，葡萄酒投资作为一种收益稳定的产品，越来越受到人们的关注。我国的葡萄酒消费群体中有相当一部分是高学历、高收入的中青年成功人士，他们在品尝美酒的同时，也逐渐认识到葡萄酒所蕴含的投资价值。

由于葡萄并非我国主要的消费农产品，国内对其价格的波动研究目前尚不多见，已有的文献主要包括：孙伟等[1]运用坎德尔秩次相关分析的方法对我国葡萄的收购价格进行了研究，认为在多种因素影响的情况下，我国葡萄的收购价格波动幅度将越来越大；周力等[2]运用CMS模型研究了我国葡萄酒进口波动的成因，认为进口引力是左右我国葡萄酒进口贸易波动的首要原因。国外研究如Gregory等[3]分析了引起葡萄酒价格波动的几个因素，包括天气条件以及由于天气条件引起的葡萄成分变化、主观的品质评价和葡萄酒陈酿的时间等，认为不同品种的葡萄酒价格对于以上因素的敏感性各不相同。

更多的价格波动性研究则针对一般的农产品和食品。任全玉[4]以食品零售价格为研究对象，将不同食品进行合理分类，重点分析每类食品价格波动特点，并预测城市居民食品零售价格的走势；李静等[5]在分析了中国食品价格波动属性的基础上，具体研究了随机因素对我国食品价格波动的冲击效应和冲击路径；王振霞[6]对我国食品价格波动的原因进行了研究，认为城乡居民人口结构的变化、脆弱的食品供给体系、不断上涨的农业生产成本和通货膨胀因素是引起食品价格波动的主要原因；马敬桂等7]研究了农产品价格对CPI和食品价格波动的影响，认为农产品价格的同期冲击影响对食品价格的冲击较大，是引起食品价格波动的主要原因；余家凤等[8]运用计量经济学的方法对粮食产量和粮食价格之间的波动性进行了研究，认为粮价的变化对粮食产量变化的影响更为显著。

葡萄酒投资作为一项新兴的投资模式，尚有许多问题值得探究。本文将选取国际葡萄酒权威指数之一的LIV-EX Fine Wine Investables Index（下文简称FWI）作为研究对象，利用GARCH族模型对葡萄酒投资指数的波动性进行建模分析。

一、数据的选取及预处理

（一）FWI的背景介绍

FWI的构成来源于波尔多地区24所顶级酒庄大约200款葡萄酒的价格，该指数自1988年1月开始发布，比LIV-EX所发布的其他指数（如LIV-EX 50、LIV-EX 100等）都要早得多。由于所选取的葡萄酒大多为高档酒，具有较高的投资价值，所以FWI可以反映葡萄酒投资市场的前景。指数以1982年Robert Parker发布的数据为基础，主要以LIV-EX中间价进行计算，同时考虑葡萄酒的生产年份和产量，对于不同类型的葡萄酒给予不同的权重。为保证指数的公正性，其构成必须满足下列三个条件：

（1）所选取的葡萄酒必须获得行业认可品酒师95分以上的品质打分。

（2）所选取的葡萄酒不早于1982年，并且必须在市场上有销售，以剔除少数不符合市场一般情况的珍藏美酒的因素。

（3）LIV-EX中间价是指某款酒在LIV-EX交易平台上最高价与最低价的平均数；但如果某款酒在过去的30天内有成交，则按成交价作为当期的中间价；此外，每款酒的中间价都由评估委员会审核保证此价格是真实可靠的。

（二）数据的选取及描述性统计

本文选取由LIV-EX发布的从1988年1月到2013年11月的FWI月度数据，共311个观测值作为研究对象。由于对时间变量进行自然对数处理能让数据达到平滑的效果，使计算结果的拟合度更高，故首先对FWI序列进行自然对数处理，形成FWI对数序列，记为LNFWI，其走势如图1所示。

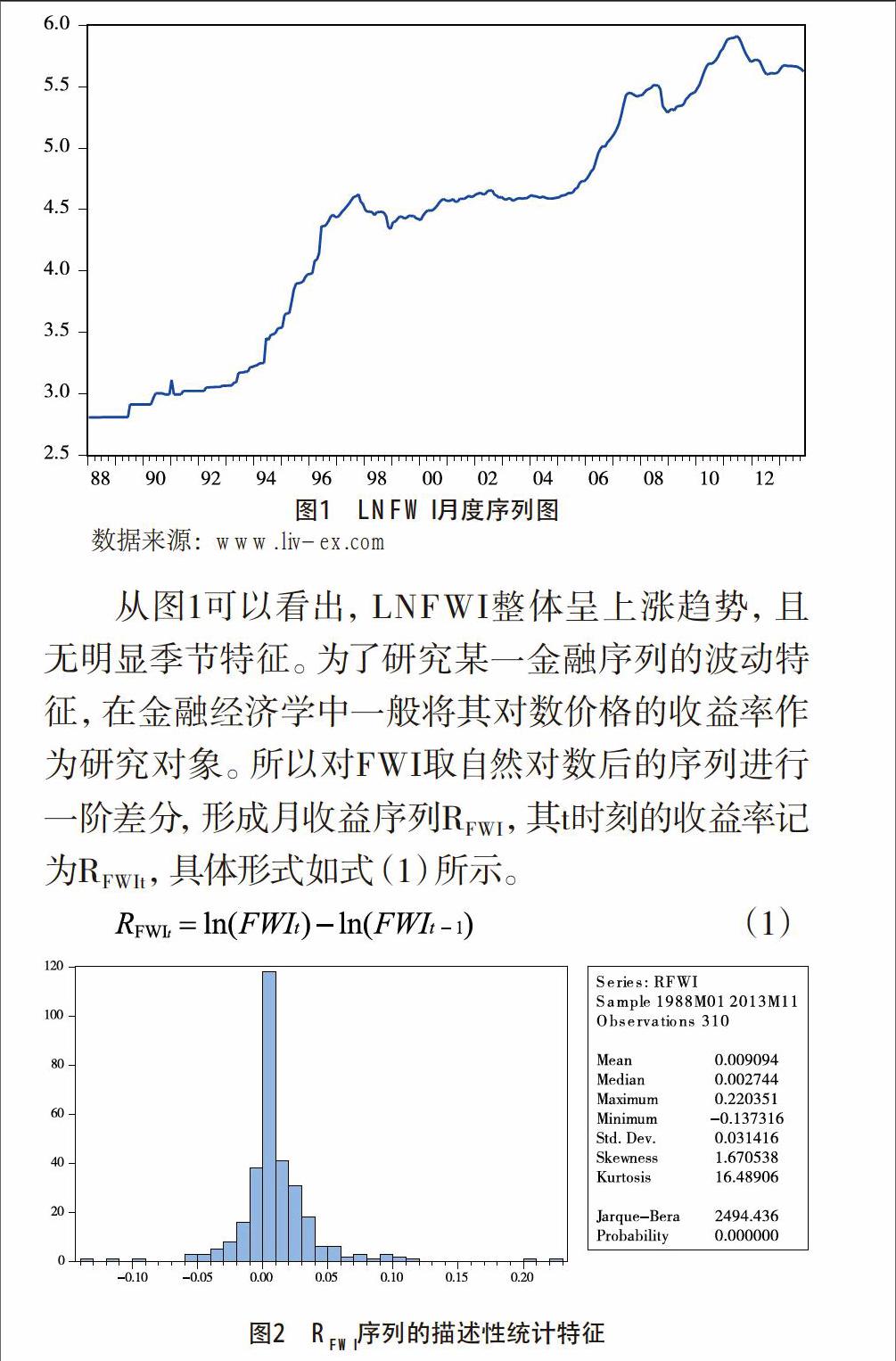
图1 LNFWI月度序列图

数据来源：www.liv-ex.com

从图1可以看出，LNFWI整体呈上涨趋势，且无明显季节特征。为了研究某一金融序列的波动特征，在金融经济学中一般将其对数价格的收益率作为研究对象。所以对FWI取自然对数后的序列进行一阶差分，形成月收益序列RFWI，其t时刻的收益率记为RFWIt，具体形式如式（1）所示。

（1）

图2 RFWI序列的描述性统计特征

由图2可以看出，该序列具有明显的“宽尾”特征，Jarque-Bera检验的结果拒绝其属于正态分布的假设；收益序列的均值为正，表明从长期来看，葡萄酒投资的平均收益为盈利水平，对其投资有利可图；偏度系数大于0，表明该收益率序列具有右偏的非对称性，说明该收益序列虽然长期为盈利水平，但从短期来看，亏损的可能性仍然不小；峰度系数远大于3，表明FWI收益率序列有尖峰厚尾的特征，说明此收益序列有较大概率取到极端值，即发生剧烈波动的概率相对较高，有波动集群的特征。

（三）平稳性及自相关性检验

只有在一组时间序列平稳的情况下，时间序列随机特征不再随时间而变化，才能建模分析其未来的变化，所以对RFWI序列采用ADF（Augmented Dickey-Fuller）单位根检验，来验证时间序列平稳性（见表1）。

表1 RFWI序列单位根检验结果

t-统计量 概率值*

-9.290573 0.0000

检验临界值 1% level -3.451421

5% level -2.870712

10% level -2.571728

*macKinnon （1996） one-sided p-values.

从检验结果来看，单位根的mackinnon临界值分别为-3.451421、-2.870712、-2.571728，t检验统计量为-9.290573，小于相应的临界值，从而拒绝原假设，表明RFWI序列不存在单位根，是平稳序列。且由图3可知，该序列围绕零值上下随机波动，没有明显向上或向下趋势，但是存在较为明显的极值，说明序列存在较大的波动性。

图3 RFWI月度序列图

接着对序列进行自相关性检验，发现序列的自相关函数拖尾，而偏自相关函数呈三阶后截尾，初步判断为AR（3）模型，首先由最小二乘法得到FWI月收益率序列RFWIt的拟合方程，如式（2）所示。

（2）

模型拟合系数的统计量见表2。

表2 RFWI序列AR（3）模型拟合系数统计量

变量 系数 标准误 t-统计量 概率值

1 0.219380 0.056624 3.874294 0.0001

2 0.140377 0.057448 2.443532 0.0151

3 0.162036 0.056638 2.860890 0.0045

调整R2 0.065602

从表2中可以发现系数的相伴概率值均小于5%的显著性水平，表明系数拟合状况良好，但是调整R2值仅有0.065602，说明模型的解释能力不强，可能存在其他影响模型解释能力的因素。进一步对模型回归方程的残差序列进行LBQ检验，发现其自相关函数拖尾，而偏自相关函数呈25阶截尾，表明FWI月收益序列回归方程的残差序列可能存在高阶ARCH效应。进一步对残差序列进行ARCH LM检验，通过引入辅助回归方程来判断是否存在ARCH效应，如式（3）所示。

（3）

式中，μt表示回归方程在t时刻的残差，εt为随机扰动项。

通过检验，得到了在滞后阶数q=25时的ARCH LM检验结果（见表3）。F检验和χ2统计量的相伴概率P值均小于5%显著性水平，表明模型中的随机误差项不仅存在异方差，且存在高阶ARCH效应，因此考虑利用GARCH族模型来刻画其条件异方差，以消除序列中的异方差。

表3 RFWI残差序列 ARCH LM检验结果

F-统计量 1.852344 概率值（25，256） 0.0097

χ2统计量 43.19767 概率值（25） 0.0133

二、基于GARCH族模型的波动性研究方法

大量实际数据表明，不同于一般的宏观经济变量，用来测度金融时间序列波动性的方差和协方差并非恒定不变，而是随时间变化的，在方差的变化过程中，幅度较大的变化往往跟随着幅度较大的变化，幅度较小的变化也往往跟随着幅度较小的变化，即通常所说的波动聚集性[9]。

（一）ARCH-M模型

Engle于1982年引入条件方差的概念分析方差变化的原因，并提出ARCH模型，指出金融时间序列yt的条件方差ht会随时间变化，因而可视ht为条件均值方程随机误差项μt滞后项的函数，即收益率的波动取决于以往的消息[10]。此外，一般金融理论认为金融资产的收益正比于其可能遭受的风险，较高的风险通常也会带来较高的平均收益。为了描述这种现象，Engle等[11]将条件方差引入到均值方程中，构成ARCH-M模型，其数学模型可表示为：

（4）

式中，ɑ1，ɑ2，…，ɑq及ω为待估参数；μt服从q阶的ARCH过程。由式（4）可知，对第i期收益率的波动影响由参数ɑi决定，q的值表示μt的某一波动情况持续的时间，因此该模型能够刻画市场的波动聚集性。

（二）GARCH模型

为解决ARCH模型中需要估计大量参数的难题，Bollerslev[12]提出了GARCH模型，把t时刻之前的条件方差加入到时刻t的条件方差函数之中，其对金融序列波动性分析和预测特别有效，GARCH（p，q）模型的基本表达式为：

（5）

式中ɑ1，ɑ2，…，ɑq；ω；β1，β2，…，βp为待估参数。ɑq，ω，βp均>0，并且GARCH（p，q）过程是平稳过程的充分必要条件是。此外，若p=0，则GARCH（p，q）过程退化为ARCH（q）过程；若p>1，q>1，则称之为高阶GARCH（p，q）过程，p，q的取值需根据拟合模型的AIC和SC值的大小来判断。但在大多数实证研究中，考虑到模型的灵活性和简约性，常用简单的GARCH（1，1）模型拟合时间序列，基本公式为：

（6）

式中，ɑ表示前一期的波动情况，其大小反映出市场的变化对本期序列波动性影响的大小；β则表示前一期的波动情况对本期序列影响所持续时间的长短。

（三）EGARCH模型

GARCH模型虽然能够解决高阶ARCH模型的拟合问题，但仍然存在不少局限性。首先，为保证条件方差不为负，它要求各参数皆为正值，然而在实际应用过程中，这个条件常常难以得到满足；其次，GARCH模型对波动性的描述是对称的，它不能反映出序列波动的非对称效应（也称杠杆效应），即市场上“利好”与“利空”的消息对序列波动性影响的不一致性。为了刻画序列波动性的非对称效应，Nelson[13]提出了EGARCH（p，q）模型，用于刻画市场“利好”“利空”消息对序列波动性影响的非对称性，其数学表达式为：

（7）

式中，EGARCH（p，q）模型的条件方差ht是用指数形式表示的，它克服了GARCH模型对参数非负的限制，并且该模型引入了参数γ（杠杆因子），使模型可以表示非对称效应（即在γ≠0的条件下，随机干扰项取正值或负值时，会使ht发生不同程度的变化）。EGARCH模型通过杠杆因子γ反映正负干扰（“利好”和“利空”消息）对波动的非对称影响：如果-1<γ<0，则表示一个负干扰（μt<0）引起ht的波动比相同程度的正干扰（μt>0）所引起的变化要大；如果0<γ<1，则表示一个正干扰（μt>0）引起ht的波动比相同程度的负干扰（μt<0）所引起的变化要大；如果γ=0，则表示ht对正负干扰的变化是对称的。

三、基于GARCH族模型的FWI月收益序列波动性分析

（一）GARCH模型的确立

由于RFWI序列回归方程的残差项具有异方差性，且具有高阶ARCH效应，使用ARCH模型对序列进行拟合时需设定较大的滞后阶数，形式复杂，因此使用GARCH模型替代原来的ARCH模型。考虑到模型的简约性，首先以GARCH-M（1，1）进行拟合，结果见表4。

表4 RFWI序列的GARCH-M（1，1）模型统计量

变量 系数 标准误 t-统计量 概率值

ρ 5.269755 4.852858 1.085907 0.2775

ω 5.83E-05 9.40E-06 6.203274 0.0000

α 0.038071 0.009060 4.201879 0.0000

β 0.902356 0.014909 60.52598 0.0000

从表4中我们可以得出以下结论：ω、α、β这三项参数估计的t统计量非常显著，其相应的概率值也非常小，且ARCH项和GARCH的各项系数估计值之和ɑ+β=0.940427<1，说明GARCH-M（1，1）为平稳过程，模型能够反映出FWI月收益率序列RFWI的异方差性，同时也说明RFWI序列具有波动集群的性质；但均值M的参数ρ的相伴概率未能通过验证，表明RFWI序列不存在ARCH in Mean效应，即对于FWI而言，其预期收益与风险可能不一定成正比关系，并非意味着预期风险越大，收益就越高。

剔除ARCH in Mean的因素后，重新对RFWI序列建立GARCH（1，1）模型（见表5）。

表 5 RFWI序列的GARCH（1，1）模型统计量

变量 系数 标准误 t-统计量 概率值

ω 0.000868 5.00E-05 17.36441 0.0000

α 0.369327 0.090313 4.089428 0.0000

β -0.212812 0.049040 -4.339555 0.0000

此时ω、α、β这三项参数估计的t统计量非常显著，其相应的概率值也非常小，且ARCH项和GARCH的各项系数估计值之和ɑ+β=0.156515<1，说明GARCH（1，1）为平稳过程。虽然此处GARCH项的参数β为负，但对本例而言，其结果并不影响条件方差ht仍然为正，所建的模型能较好地拟合RFWI序列，其条件方差序列图如图4所示。

图4 GARCH（1，1）条件方差序列图

（二）EGARCH模型的确立

为了刻画出FWI波动的非对称性，即FWI对不同外部消息刺激的反应程度，在上文GARCH（1，1）模型的基础上进一步运用EGARCH模型对其月收益率序列的RFWI的波动性进行分析，建立EGARCH（1，1）模型（见表6）。

表6 RFWI序列的EGARCH（1，1）模型统计量

变量 系数 标准误 t-统计量 概率值

ω -11.43678 0.482245 -23.71573 0.0000

α 0.367793 0.053763 6.840965 0.0000

γ 0.145432 0.043124 3.372407 0.0007

β -0.559252 0.065038 -8.598800 0.0000

从表6可以看出，ω、α、β、γ参数估计的t统计量非常显著，其相应的概率值也非常小，表明EGARCH（1，1）模型拟合情况良好。从以上数据分析可见，γ=0.145432，说明FWI的月收益率序列具有非对称的杠杆效应，且外部市场“利好”消息对该序列波动的影响程度大于“利空”消息的影响程度。当葡萄酒投资市场出现“利好”消息时，非对称效应参数ɑ+γ=0.513225，即“利好”消息会给FWI月收益率的条件方差带来0.513225倍的冲击；而当市场出现“利空”消息时，非对称效应参数ɑ-γ=0.222361，即“利空”消息会给FWI月收益率的条件方差带来0.222361倍的冲击。可见葡萄酒投资市场的波动具有正向非对称，市场上的“利好”消息比等量的“利空”消息对葡萄酒投资市场产生的冲击明显更大，说明虽然葡萄酒投资市场的波动具有非常明显的非对称性，且“利好”消息对指数波动的影响要远大于“利空”消息的影响。

四、结果分析

（一）基于GARCH（1，1）模型的结果分析

从GARCH（1，1）建模的结果来看，FWI的月收益序列在1991、1994、1996和2008年分别有四个比较大的波动，具体分析如下：

1.1991和1994年。从表7可以看出，法国葡萄酒的需求量从1986年开始一直到1995年左右一直在下降，而其产量在经历20世纪80年代后期的大幅下降后从1991—1992年开始回升（虽然缺乏1991和1992年的产量数据，但是从1991—1995年的平均产量和1993—1995的产量中可以看出，法国葡萄酒的产量在1991—1995年处于上升轨道）。受供需不平衡的影响，在1991和1994年左右法国葡萄酒的平均价格有两次较为明显的下跌行情（如图5所示），尤其是1994年，跌至近些年的底点。受价格下跌的影响，FWI在这两年附近出现了剧烈的波动。

表7 1986-1998年法国葡萄酒生产和消费数据（单位：hl）

1986-

1990年 1991-

1995年 1993年 1994年 1995年 1996年 1997年 1998年

产量 64641 52886 52059 53325 54354 57047 53561 52671

消费量 41715 37310 37354 36663 36515 34795 35500 35800

数据来源：OIV

图5 1988-2000法国葡萄酒价格（单位：法郎/hl）

数据来源：OIV

2.1996年。在1996年葡萄酒的消费量进一步下滑而产量继续上升的情况下平均酒价反而攀升到近些年的高点，其背后的主要原因是增加的产量主要为了满足出口的需要。据OIV统计[14]，法国葡萄酒1996—2000年的平均出口量较1991—1995年增长了33%，其主要原因是以中国为首的新兴国家葡萄酒需求大幅增长。以中国为例，其1995年的葡萄酒消费量较1994年上涨了43%，2000年比1996年更是增长了近80%，而其自身产量到了1999年才出现比较大的涨幅，显然在1995—1998年产量和消费量之间的缺口需要由进口酒来填补，其中法国则是最主要的来源。高涨的出口热情拉动了葡萄酒价格的上涨，也使FWI出现了较为明显的波动。但随之而来的东南亚金融危机最终影响到全球经济，造成葡萄酒价格在1997—1998年处于较低的水平，FWI受其影响，也出现了小幅但比较明显的波动。

3.2008年。据全球主要的商业拍卖行发布数据显示，2007世界范围内的精品葡萄酒拍卖额比2006年上升了25%，达到了3.1亿美元，美元汇率的下跌使美国占主导地位的竞标吸引了很多买家。2008年前三季度，各大拍卖行交易额均呈增长趋势，珍稀葡萄酒很好地抵御了经济衰退的影响。然而10月之后，全球金融市场彻底崩溃，葡萄酒市场也不可避免地跟着迅速跌落。2008年全球拍卖行精品葡萄酒交易额从上一年的3.1亿美元降至2.76亿美元，不过与主要的股指相比，8%的跌幅并不算很大，这从另一方面也表现出葡萄酒投资具有一定的抵御风险性。

而从日常葡萄酒的价格来看，受金融危机的影响，法国葡萄酒的价格跌至近1994年以来的最低点。但这并非完全是由经济危机造成的，2004年全球葡萄酒产量过剩达到最高点（如图6所示），之后葡萄酒价格便不断走低，并一直在低位波动，而之后受金融危机的影响在2008年达到最低，不过此后便开始逐步回升（如图7所示）。本文认为造成这一现象的原因在于葡萄酒在西方国家属于日常消费品，具有较强的刚性需求，其价格受供需平衡的影响要大过经济危机的影响。

图6 世界红酒产销差额（单位：Mhl）

数据来源：OIV

（二）基于EGARCH（1，1）的FWI杠杆效应分析

从图1可以看出，FWI从1992年开始有上升的趋势，而在1994—1996年几乎呈现垂直上升，正是受1992年下半年开始的葡萄酒价格下跌的影响；2004—2008年和2009—2011年也出现了同样的现象。本文分析认为葡萄酒价格下跌对FWI的投资而言并非是“利空”的坏消息，反而代表出现了一个可以低价买入的投资好时机，是“利好”消息。同时也可以发现，1997年开始的东南亚金融危机及2008年下半年出现的全球经济危机对FWI波动的影响并没有其受葡萄酒价格下降带来的影响更为明显，这与一般认为的经济危机可能对金融指数带来较大波动影响并不相符，其原因在于FWI的杠杆系数γ为正，且ɑ+γ值与ɑ-γ值相差近两倍，结果造成其对“利空”消息的敏感度远不如对“利好”消息的敏感度。

图7 1997-2008法国葡萄酒价格（单位：欧元/hl）

数据来源：OIV

五、结束语

1.从FWI的对数序列LNFWI月序列图（图1）中可以看出，对于长期投资而言，FWI具有明显的上涨趋势。进一步分析其月收益率RFWI序列的基本统计概况可以发现，FWI具有一般金融收益序列的非正态分布、尖锋厚尾、异方差和波动集群等特征。

2.使用AR（3）模型能较好地拟合RFWI序列，但进一步使用GARCH-M（1，1）模型研究发现其不存在ARCH in Mean效应，这不符合一般金融序列的收益与风险成正比的普遍现象。本文认为虽然FWI是一种金融衍生产品，但由于葡萄酒本身在西方国家是一种日常消费品，具有一定的刚性需求，FWI波动不像其他金融产品那样对经济的变化敏感。去除Mean的因素后使用GARCH（1，1）模型便能较好地拟合FWI的波动特征，发现其在1991、1994、1996和2008年分别存在四个比较大的波动，但与股票债券等高风险金融产品相比，FWI的波动幅度明显较小。

3.使用EGARCH（1，1）模型拟合了FWI月收益序列的杠杆效应，反映出“利好”和“利空”消息对FWI的影响程度。研究发现葡萄酒投资市场的波动具有明显的非对称效应，市场对“利好”消息的敏感度远大于对“利空”消息的敏感度，表现出反杠杆效应，这表明葡萄酒投资市场抵御风险的能力较强，一般的“利空”消息并不会对葡萄酒投资市场造成较大的冲击；相反，若是受“利好”消息的影响，则葡萄酒投资市场会受到正向的冲击，带动指数上涨，从这点来看，葡萄酒的投资具有广阔的前景。正如伦敦国际葡萄酒交易所负责人詹姆斯·迈尔斯所说：“投资葡萄酒并非万能药，你必须睁大眼睛。在经济市场长期混乱的局面中，葡萄酒的价格也会下降。但是这一下降不像债券、股票、地产市场那样萎靡，葡萄酒的前景看上去仍很强劲。”

孙伟，周志坚，穆维松.葡萄收购价格的波动特征分析[J].中外葡萄与葡萄酒，2011（7）：69-71.

周力，应瑞，瑶江艳.我国葡萄酒进口贸易波动研究—基于CMS模型的因素分解[J].农业技术经济，2008（2）：25-31.

Gregory V Jones，Karl-Heinz Storchmann.Wine market prices and investment under uncertainty： an econometric model for bordeaux Crus classes[J].Agricultural Economics，2001，26（2）：115-133.

任全玉.基于价格指数的食品价格波动分析[J].中国商贸，2012（22）：90-91.

李静，楠玉.我国食品价格波动冲击路径的随机因素分析[J].经济经纬，2013（2）：28-32.

王振霞.我国食品价格波动原因及价格稳定机制研究[J].财贸经济，2011（9）：113-119.

马敬桂，黄普.农产品价格对CPI和食品价格的冲击效应分析—基于VAR模型的实证分析[J].长江大学学报（自然科学版），2011，8（9）：256-260.

余家凤，孔令成，龚五堂.粮食产量与粮价波动关系的再研究[J].经济问题，2013（1）：108-111.

Tsay R S.金融时间序列分析[M].潘家柱，译.北京：机械工业出版社，2006.

Engle R F.Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation[J].Econometrica，1982（50）：987-1008.

Robert F Engle，David M Lilien，Russel P Robins.Estimating time varying risk premia in the term structure：the ARCH-M model[J].Econometrica，1987，55（2）：391-407.

T Bollerslev.Generalized auto regressive conditional heteroskedasticity[J].Journal of Econometrics，1986（31）：307-207.

Nelson D B.Conditional heteroskedasticity in asset returns：a new approach[J].Journal of Econometrics，1991，59（2）：347-370.

G Dutruc-Rosset.The state of vitiviniculture in the world and the statistical information in 2000[R].Belgique：International Office of Vine and Wine，2001.

[责任编辑 王艳芳]