供应链企业间知识共享的博弈分析

王洁

（内蒙古工业大学管理学院，呼和浩特010051）

供应链企业间知识共享的博弈分析

王洁

（内蒙古工业大学管理学院，呼和浩特010051）

以制造商和零售商组成的二级供应链为研究对象，通过构建完全信息静态博弈和完全信息动态博弈模型，探讨供应链企业知识共享的决策行为，并且分析了激励在知识共享中的作用。

供应链；知识共享；博弈；激励

近年来国内外学者对供应链中知识共享问题进行了一些相关性的研究。朱庆、张旭梅研究发现供应链知识共享行为的影响因素有知识共享能力的差异、知识共享风险、有效的激励和统一的知识共享平台［1］。李家清指出供应链知识共享的制约因素有共享制度不健全、信任程度低、成本收益不对称、共享能力差异和缺乏有效激励［2］。国内学者张庭发、张玉明针对在供应链节点企业之间知识共享的博弈，比较分析静态和动态斯塔克尔伯格（Stackelberg）博弈，探讨了两种情况下的均衡解和利益分配问题［3］。冯长利等人运用演化博弈理论对供应链成员企业的知识共享行为的演变途径进行了探讨，研究发现降低共享成本与风险、提升知识吸收能力与合作效应、加大知识投入量以及建立良好的激励机制，是促进供应链成员企业知识共享、提升供应链整体竞争力的必由之路［4］。陈建新等人针对供应链各节点企业在知识共享中可能产生的博弈，分析了博弈的纳什均衡策略，并利用纳什的讨价还价模型对合作博弈中由知识共享产生的利益分配问题进行了探讨［5］。

供应链中的企业是否进行知识共享，从本质上看是企业间的博弈问题，某一企业是否进行知识共享不仅取决于他自己的行为，而且取决于与之交易的另一企业的行为。供应链中节点企业的参与，构成博弈参与人，每个参与人的决策不同，构成了博弈策略空间，而且各自在供应链的利润不同，从而构成了各自的支付函数。

供应链环境下各成员企业之间是一种合作伙伴关系，对于双方的信息都比较了解，所以通过构建完全信息下静态、动态博弈模型来分析激励对供应链企业间的知识共享策略的影响［6］。本文从定量角度出发，通过博弈论方法研究了供应链中企业知识共享问题。

一、供应链企业间知识共享的完全信息静态分析

（一）博弈模型假设

供应链企业间的关系总体上概括为供应方与需求方的关系。在进行经济活动时具体表现为供应商与制造商、制造商与分销商、分销商与零售商、零售商与最终用户之间的关系［7］。

为了方便对供应链企业间知识共享问题的研究，本文选取由单一制造商和单一零售商构成的两级供应链进行分析。这两个节点是供应链上下游中重要的两个节点，分别是生产环节和销售环节。二者之间会有大量的业务往来，在互动过程中，很容易产生知识的流动。下面就对制造商和零售商之间的知识共享进行博弈分析。为了便于研究，特做如下假设：

（1）只存在制造商和零售商两个博弈方，二者进行策略选择不受外部环境干扰；

（2）在制造商和零售商进行合作时，都具有两种选择：与对方进行知识共享与不进行知识共享；

（3）假设制造商和零售商的知识水平相当，且都了解对方的收益，即确保此次博弈是在完全信息条件下进行；

（4）制造商和零售商都具有理性，都以利润最大化的原则作出最优选择；

（5）π1、π2＞0，y＞0；

（6）此次博弈行为只发生一次。

（二）博弈收益矩阵

制造商和零售商的收益矩阵如图1所示。

（三）博弈模型分析

若双方不进行知识共享，二者在知识共享行为中的收益为0。若一方采取知识共享，而另一方不进行知识共享，则选择不共享的一方会因为其投机行为获得额外的收益y，而共享的一方则会损失y。若双方都选择进行知识共享，则二者收益分别为π1、π2。

图1　制造商和零售商收益矩阵

（1）对于制造商而言，如果零售商选择“共享”，它获得的收益分别是 π1和π1+y，根据理性人假设，以追求利益最大化为目标，它会选择“不共享”；如果零售商选择“不共享”，它的收益分别-y是和0，根据利益最大化原则，制造商会选择利益为0的策略，即“不共享”。因此，（不共享，不共享）是制造商的占优策略。

（2）对于零售商而言，如果制造商选择 “共享”，它获得的收益分别是π2和π2+y，同样，根据理性人假设，以追求利益最大化为目标，它会选择“不共享”；如果制造商选择“不共享”，它的收益分别是-y和0，根据利益最大化原则，零售商会选择利益为0的策略，即“不共享”。因此，（不共享，不共享）是零售商的占优策略。

（3）制造商、零售商行为的共同结果。在该博弈中，（不共享，不共享）是唯一的纳什均衡。在知识共享中，制造商和零售商都具有“不共享”的占优策略，即对于任一方而言，无论对方作何选择，“不共享”是其最优策略，从而陷入了囚徒困境。

（四）负激励对供应链知识共享的影响

由以上博弈结果可知，在一方采取知识共享时，另一方选择知识不共享带来的收益更大。这是由于不共享的一方采取了投机行为，而采取这种投机行为却没有付出任何代价。因此，有必要采取惩罚措施即负激励对参与方进行约束。

图2　负激励下制造商和零售商的收益矩阵

负激励下制造商和零售商的收益矩阵如图2所示。

其中，w表示不进行知识共享时惩罚造成的损失。

当π1＞π1+y-w，π2＞π2+y-w时，即y-w＜0条件下制造商与零售商会选择知识共享。最终的博弈结果为（共享，共享），原有的囚徒困境被打破。所以，当惩罚（负激励）带来的损失大于投机行为带来的收益时，会使企业主动进行知识共享。

二、供应链企业间知识共享的完全信息动态博弈分析

在实际情况下，制造商和零售商很少同时行动，而是先后行动，而且双方在做决策时都清楚对方的策略和效用函数，对博弈过程中对方的特征、战略空间及效用函数都有准确的信息，属于完全信息。本文主要采用动态博弈中的斯塔克尔伯格方法对博弈模型求解。因此，探讨知识共享在完全信息下进行斯塔克尔伯格主从博弈。制造商处于供应链的核心地位，在博弈过程中，制造商是主导者，而零售商是追随者。

（一）博弈模型假设

1.符号设定

知识学习能力L：学习能力越强，知识转化率越高；

知识投入成本I：如通过会议方式进行知识共享所需的成本；

知识共享风险R：知识的共享会使企业失去自身优势，从而产生风险；

知识投入量X：企业对所拥有的知识愿意共享的知识量；

生产加工成本C：企业对产品的生产和再加工产生的成本。

2.基本假设

（1）制造商以Pm的转移价格将产品转移给零售商，零售商再以Pr的价格销售给市场。逆需求函数为Pr=a-bq。Q为市场需求量，即零售商向制造商的订货量为q。

（2）假设制造商与零售商与双方共享的知识具有互补性，制造商和零售商提供给对方的知识量分别为Xm和Xr。

（3）假设进行知识共享后制造商的单位成本函数Cm=A-LmXr，零售商的单位成本函数为Cr=BLrXm。制造商对于原材料进行生产加工的单位成本为A，零售商对原材料加工的单位成本B。本文采用线性函数来表示知识共享量和知识转化能力与成本之间的关系，但是需要说明的是当知识共享量和知识转化能力达到一定程度时，单位成本将会固定在某一值。

（4）πm为制造商的收益，πr为零售商的收益：

制造商的收益；πm=（Pm-Cm）q-RmXm-I=（Pm-A+LmXr）q-RmXm-I；

零售商的收益。πr=（Pr-Pm-Cr）q-RrXr-I=（Pr-Pm-B+LrXm）q-RrXr-I。

（二）博弈模型分析

基于斯坦克尔伯格博弈的决策模型，制造商处于主导地位，零售商处于从属地位。下面分两个阶段进行决策。第一阶段，制造商确定转移价格Pm；第二阶段，零售商确定它的订货量q。最后，根据利益最大化原则确定各自的转移知识量。

采用逆推归纳法，首先对第二阶段博弈进行分析：零售商根据利益最大化原则选择自己的最优订货量q，对零售商的收益函数求一阶偏导，并令一阶偏导等于零：

第一阶段：制造商预测到零售商将以q来选择订货量，制造商针对零售商的反应做出决策，选择使自己获取最大利益的Pm。将（1）式代入πm，得：

根据前两阶段，确定知识转移量：分别将和q代入利润函数，得零售商的利润：

对πr求导，令一阶导数为零，得到零售商的知识转移量Xr：

制造商的利润：

对πm求导，令一阶导数为零，得到制造商的知识转移量Xm：

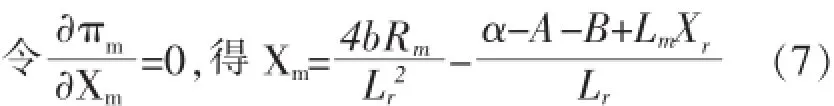
（三）结论

结论三：在相同的知识共享量与知识学习能力下，处于主导地位的企业会获得更多的利润。由（4）式与（6）式可知，当RmXm=RrXr时，进行知识共享时，制造商取得的利润大于零售商。

（四）激励作用下的供应链企业间知识共享

1.博弈分析

在激励机制中，应用最普遍的是价格激励。因此在此建立价格与订货量的函数：=Pm-cq，订货量越大，制造商的转移价格越低，其中c为制造商给零售商的折扣率。

同样采用逆向归纳法，首先由零售商选择自己的最优订货量q，对零售商的收益函数求一阶偏导，并令一阶偏导等于零：

将未采取激励措施前的Pm代入（8）式，得激励后的订货量：

根据前两阶段，确定知识转移量：分别将和代入利润函数，得零售商的利润：

制造商的利润:

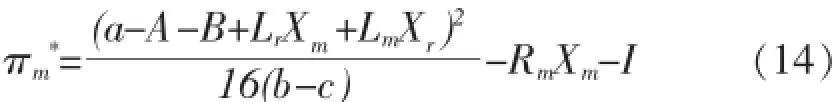
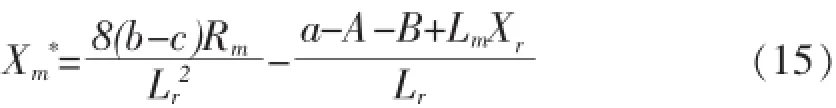
2.结论

（1）在价格激励下，零售商的订货量增加。由（3）式和（9）式可知，

（2）激励机制下，制造商和零售商的利润、共享的知识量并不一定增加。

通过对比实施激励机制前后的利润和知识共享量发现，双方利润和共享知识量是否增加，取决于需求价格弹性b和价格折扣c。要使激励机制发挥促进知识共享以及增加双方利润的作用，须满足以下条件：

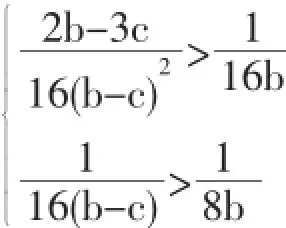
三、结束语

通过完全信息静态及完全信息动态模型，研究供应链企业间知识共享的过程，并分析激励对于知识共享的影响，得出以下结论：（1）静态博弈下，负激励会促进企业进行积极的知识共享；（2）动态博弈下，由于企业所处地位不平等，在相同的知识共享量与知识学习能力下，处于主导地位的企业在知识共享行为中会获得更大的利益；（3）动态博弈下采取激励机制，企业的利润和知识共享量并不一定增加，在满足一定条件下才会增加企业利润，增大知识共享量。

［1］朱庆，张旭梅.供应链企业间的知识共享机制研究［J］.科技管理研究，2005（10）：73-75.

［2］李家清.供应链知识共享制约因素及共享机制研究［J］.未来与发展，2010（3）：55-59.

［3］张庭发，张玉明.基于博弈论的供应链节点企业知识共享分析［J］.统计与决策，2011（17）：184-186.

［4］冯长利，周剑，兰鹰.供应链成员间知识共享行为演化博弈模型［J］.情报杂志，2012（3）：138-144.

［5］陈建新，谢磊，土建东.供应链知识共享的博弈分析［J］.科技进步与对策，2009（8）：142-145.

［6］张维迎.博弈论与信息经济学［M］.上海：上海人民出版社，1996.

［7］马士华，林勇，陈志祥.供应链管理［M］.北京：机械工业出版社，2000.

（编辑：徐永生）

An Analysis of the Knowledge-Sharing between Member Enterprises of the Supply Chain in Terms of Game Theory

WANG Jie
（Management College，Inner Mongolia University of Technology，Hohhot 010051，China）

Taking two-stage supply chains with a manufacturer and a retailer as its object，this research constructs complete game models of both static and dynamic information，explores supply chain enterprises’decision-making process regarding knowledge-sharing and analyses the roles that incentives can play in knowledge-sharing.

supply chain；knowledge-sharing；game theory；incentive

F 224.32

A

1671-4806（2015）05-0042-04

2015-08-04

王洁（1990— ），女，内蒙古巴彦淖尔人，硕士研究生，研究方向为物流与供应链管理。