倾斜中厚矿体采场宽度优化
罗周全,汪伟,谢承煜,贾楠,姚曙,颜克俊,曹胜祥,向军
倾斜中厚矿体采场宽度优化
罗周全1,汪伟1,谢承煜1,贾楠1,姚曙2,颜克俊2,曹胜祥2,向军2
(1. 中南大学资源与安全工程学院,湖南长沙,410083;2. 凡口铅锌矿,广东韶关,512325)
采用弹性力学分析得到顶板受力状态与采场宽度的关系,在计算所得采场安全开采最大宽度为12.1 m的基础上,结合矿山实际开采条件,提出采场结构参数初选方案;运用数值分析方法模拟获取不同结构参数下采场的力学响应特征;采用多目标决策理想点法综合考虑安全和经济两大因素,计算各方案评价指标集与理想解的向量相似度,得到各方案的优越度排序,最终实现采场结构参数的综合优化。研究结果表明:在开挖过程中,最大压(拉)应力与矿房宽度和矿柱宽度成正比,塑性区体积与矿房宽度成正比,安全率与矿房宽度成反比;矿房宽为 12 m、矿柱宽为8 m的方案为综合考虑安全与经济因素的开采最佳结构参数方案。
倾斜中厚矿体;大直径深孔采矿法;弹性力学;数值分析;理想点法
一些矿山历经长期高强度开采,现已进入深部开采阶段。近年来,随着生产规模的不断扩大,矿山设计部门在机械化盘区向上分层充填法和普通充填法的基础上,对深部形态较规则的倾斜中厚矿体采用大直径深孔采矿法,以大幅提高采矿效率,满足矿山年产量的要求。倾斜中厚矿体[1]因其特殊产状在开采过程中存在地压问题较难控制、采切工作量大、开采成本高、生产效率低等问题,是国内外公认的难采矿体,因此,在保障开采安全的基础上,充分回收矿产资源、提高生产效率是设计部门必须考虑的重要问题。合理的采场结构参数是实现矿山安全高效开采的前提[2]。对于开采倾斜中厚矿体的结构参数确定,许多研究者进行了相关研究,如:吴爱祥等[3]在室内放矿实验的基础上,通过三维放矿数值模拟得到优化的结构参数;陶干强等[4]运用有限元软件ABAQUS分析力学响应指标随不同结构参数的变化,对比得到最佳结构参数方案;王新民等[5]综合层次分析法和模糊数学法提出了一种优选结构参数的FAHP方法。以上方法虽取得了较好的研究结果,但也存在一些不足,如在确定结构参数初选方案时,多数研究以经验类比法和主观判断为主,缺乏合理依据;相似实验耗时、耗力,成本较高;而数值分析方法多以力学响应指标(安全因素)作为评价结构参数优劣的唯一标准,缺乏对其他因素(如经济因素)的全面考虑。为此,本文作者将针对国内某铅锌矿山开采倾斜中厚矿体实际,在采用弹性力学分析获得结构参数初选方案的基础上,运用数值分析手段和多目标决策理想点法,综合考虑安全和经济两大类因素,最终实现开采结构参数的优化。
1 工程概况
1.1 矿体赋存概况
设计范围内矿体为倾斜中厚矿体,平均厚度为 30 m,总体趋势为自东向西倾斜,下盘倾角平均为40°,下盘倾角稍陡,上盘倾角缓。矿体赋存于D2db和D3ta这2种围岩中,中等稳固,普氏系数为4~9。在上盘接近拉低水平处局部受断裂构造影响,有较小断层形成。矿段主要充水源为深层裂隙承压水,含水层富水性弱,水文地质条件简单。
1.2 采矿工程布置
应用大直径深孔采矿法开采倾斜中厚矿体的工程布置见图1:采场垂直于矿体走向布置,采场高度为中段高度(40 m),长度为矿体厚度。采场上部布置凿岩硐室,下部布置无底柱平底出矿结构,上下部硐室高度均为4 m。以切割天井作为首次爆破的自由面和补偿空间,分次分层侧向崩矿。出矿设备采用3 m3进口遥控铲运机,全部矿石出矿完毕,清理空区,对空区进行嗣后充填。
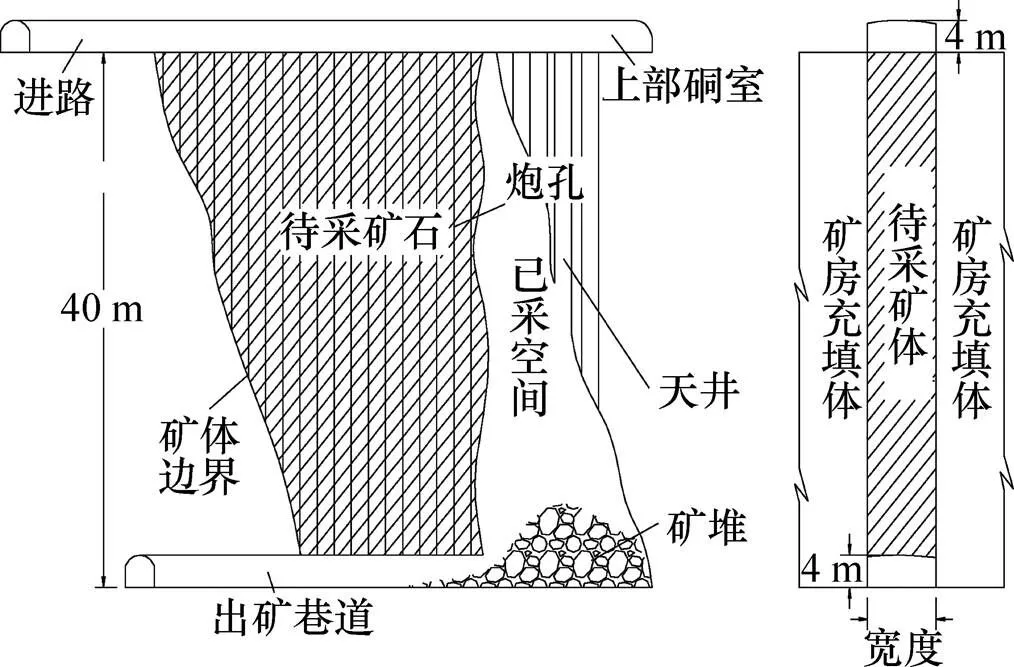
图1 开采设计剖面
在设计范围内布置2个矿柱采场和1个矿房采场。回采时沿矿体走向先采两帮矿房采场,对采空区进行全尾砂胶结充填,最后回采矿柱采场。
2 安全结构参数方案初选
2.1 力学分析
针对开采倾斜中厚矿体的实际工程布置(采场长度为矿体厚度,高度为中段高度),结构参数优化主要解决矿房采场和矿柱采场宽度的合理取值问题。研究表明[6],以阶段空场落矿为基本特征的倾斜中厚矿体采场,其稳定性状态往往由顶板要素决定。故可对顶板受力状态进行分析,确定采场安全开采宽度的合理取值。
将顶板简化为受上覆岩层均布载荷作用的三维板状结构[7],见图2。通过分析其受力状态,便可确定顶板的稳定性状况。设采场长、宽和顶板厚度分别为,和,薄板四周简化为固定支撑。

图2 顶板受力示意图
根据弹性力学小变形薄板理论,顶板受到上覆岩层均布载荷的作用,可运用瑞利−李兹法[8]解出其挠曲函数为
式中:==3,5,7,…。进一步推导可得
由式(2)及弹性力学理论得到顶板内应力为
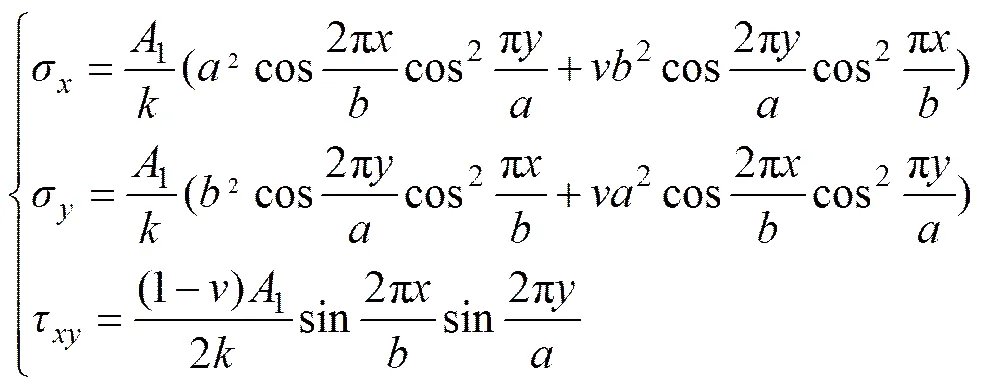
其中:1为任意常数。
由式(3)推导出最大主应力关系为
根据H·Tresca屈服准则,顶板内某点产生剪切屈服时的主应力条件为
将式(5)代入式(4),得
式中:为泊松比;为弹性模量;为顶板上覆岩层容重;为顶板厚度;为作用于顶板的覆岩厚度;为安全系数;和分别为采场长度和宽度;max为顶板内最大剪应力。判断顶板稳定的依据为
其中:[σ]和分别为顶板岩体的抗拉和抗剪强度。采场上覆围岩为D2db,岩体容重=2.720 t/m3,作用于顶板的覆岩厚度=100 m(距上部采空区的距离),泊松比=0.23,安全系数=1.5,顶板厚度=10 m(实际的采准布置),采场长=48 m(取上部硐室长)。
通过计算得到顶板受力状态与采场宽度的关系如图3和图4所示。比较计算值与岩体抗剪和抗拉强度即可确定开采宽度的安全取值。
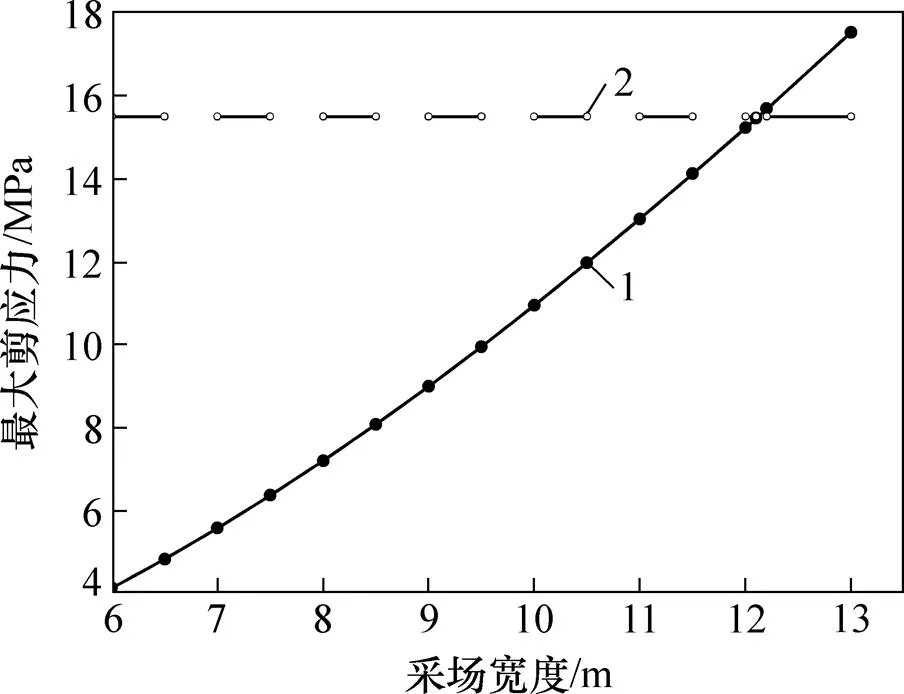
1—计算值;2—抗剪强度
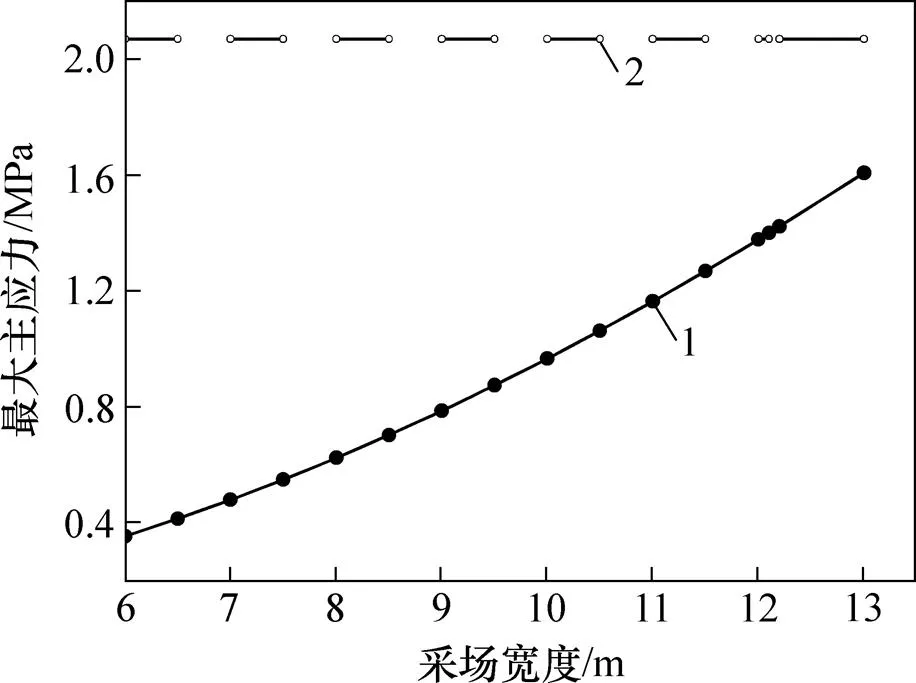
1—计算值;2—抗拉强度
由计算结果可知:当开采宽度取12.1 m时,顶板内最大剪应力及最大拉应力分别为15.46 MPa和1.40 MPa,均小于岩体的抗剪强度(15.5 MPa)和抗拉强度(2.02 MPa),顶板将处于稳定状态;当开采宽度大于12.1 m时,最大剪应力将超过顶板岩体的抗剪强度,顶板将会产生失稳破坏,故从安全角度确定采场开采的最大宽度为12.1 m。
2.2 结构参数方案初选
根据矿山开拓采准工程布置及开采设备等实际开采条件和力学分析结果,取矿房采场宽度为8,10和12 m。对于矿柱采场,考虑其两帮均为充填体,充填体强度较低且质量分布不均匀,难以保证应力集中状态下采场的稳定性,故取矿柱采场宽度为6,8和10 m。由此确定结构参数(矿房宽、矿柱宽)初选方案分别为:① 8 m和6 m;② 10 m和6 m;③ 12 m和6 m;④ 8 m和8 m;⑤ 10 m和8 m;⑥ 12 m和8 m;⑦ 8 m和10 m;⑧ 10 m和10 m;⑨ 12 m和10 m。
3 数值分析
3.1 力学实验
为准确获得岩体力学参数,深入到矿山深部(−360~−600 m中段)进行取样,采集赋存范围内矿体、围岩和充填体等7种岩样,加工成91个标准试件进行力学实验。实验项目包括:密度实验;弹性波测试;单轴抗压实验;变形实验;拉伸强度实验;抗剪断实验。根据开采矿体赋存情况,归类处理后考虑4种岩性。以室内力学实验结果为依据,通过工程折减得到相应的岩体力学参数,结果见表1。
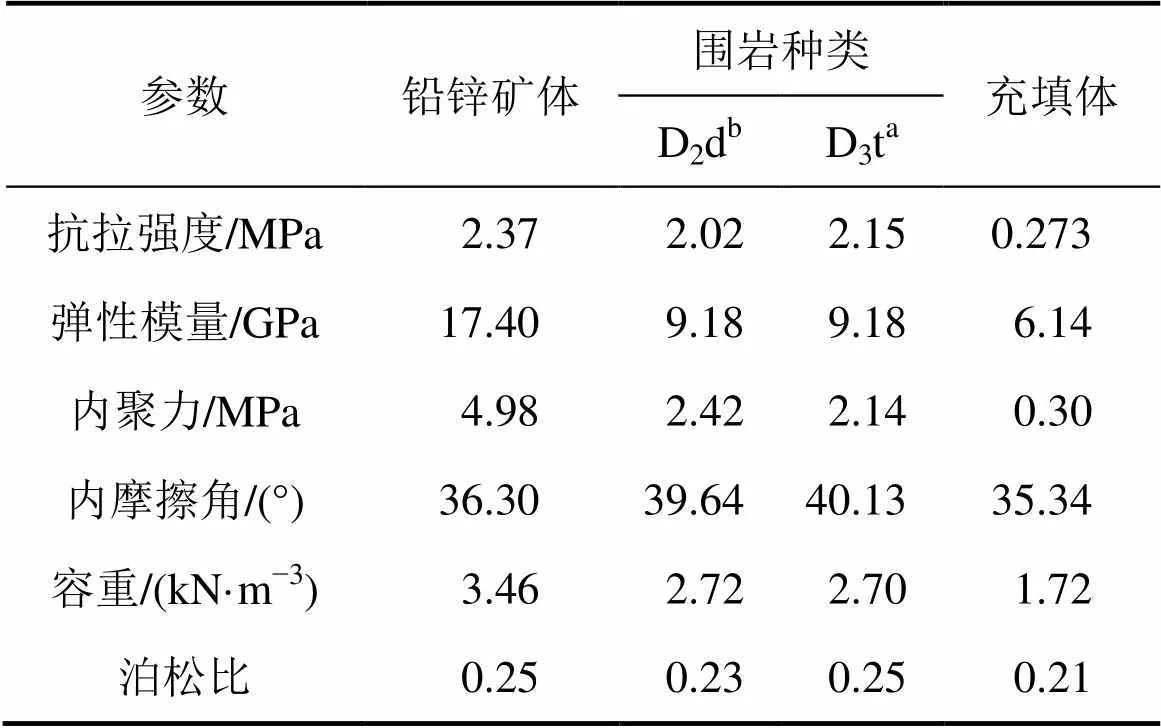
表1 岩体力学参数
3.2 数值分析模型构建
通过Surpac建立开采区域内矿体和地质断层的块体模型,经转换接口[9]导入FLAC3D软件中,得到符合真实赋存条件的三维网格模型,见图5。
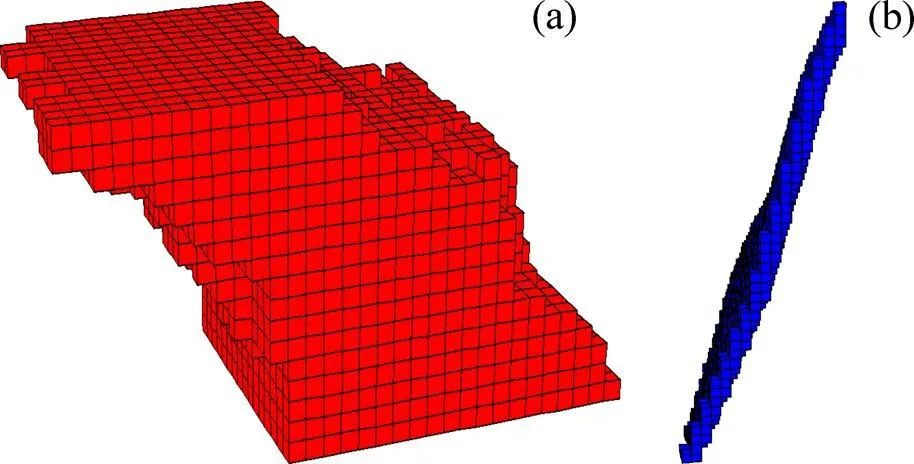
(a) 矿体模型;(b) 断层模型
圣维南定理提出:若作用于物体表面上的外力,用1个静力等效的力系代替,则距该区域较远部分所受的影响可忽略不计。基于此定理,数值分析中广泛采用开挖范围的3~5倍作为边界[10]。据此,取本文计算模型长×宽×高为150 m×100 m×100 m。模型单元数为189 342个,节点数为200 365个。计算选用摩尔−库仑屈服准则。
3.3 初始应力场及边界条件
该中段原岩地应力参数采用长沙矿山研究院的现场实测数据[11]。初始地应力场的反演采用构造应力场与自重应力场的叠加,通过快速应力边界法在模型表面施加应力边界条件并保持恒定,在计算达到平衡后将节点速度和位移清零,再对模型边界施加固定位移约束,形成初始应力场。
3.4 模拟结果及分析
以方案①(矿房宽为8 m、矿柱宽为6 m)为例,分析开挖后应力和位移场的分布规律。为便于说明,通过tecplot对输出图形进行后处理。剖面上最小主应力分布见图6。

图6 X剖面上最小主应力分布
由图6可知:开挖所造成的扰动影响为开挖范围的2~3倍;采空区两帮充填体的变形趋势与围岩的变形趋势一致(图中箭头指向);上部充填体变形以沉降为主,下部充填体变形以底鼓为主,说明充填体对位移变形的限制作用;充填体内形成了部分拉应力区(FLAC3D中定义压应力为负,拉应力为正),拉应力最大值为1.96 MPa,超过了充填体的抗拉强度(0.27 MPa),充填区域将产生失稳破坏。
研究表明:剖面上最大主应力分布和最小主应力分布集中于采场边界和角点处,最大主应力为−31.26~−0.44 MPa,最小主应力为−17.85~1.45 MPa;采场底部和东西边界处形成了拉应力区,最大拉应力为1.45 MPa,小于围岩的抗拉强度,采场处于稳定状态。
位移场分布规律见图7。从图7可以看出:距采空区越远,位移变化越小;竖向位移范围为0~3.73 cm,最大竖向位移出现在采场顶板;水平位移范围为0~2.76 cm,最大水平位移出现在西头边界。竖向位移是影响顶板稳定性的主要因素之一,总的来看,竖向位移均值较小,对采场稳定性影响不大。

图7 位移分布
3.5 方案力学响应对比分析
选取最大压(拉)应力、塑性区体积、竖向最大位移、安全率等作为评价开采方案安全性的指标。需说明的是:安全率是以计算Mohr应力圆心到破坏包洛线距离与应力圆半径之比为原理评价对象安全程度的指标,工程中[12]以安全率取2为单元的极限破坏准则,其计算公式为
式中:为安全率;1为最大主应力;3为最小主应力;为内摩擦角;为黏聚力。
获得各方案的力学响应指标见表2。从表2可见:方案①(矿房宽为8 m、矿柱宽为6 m)在各项安全评价指标上均优于其他方案。单从安全开采的角度而言,方案①为最佳的开采结构参数方案。
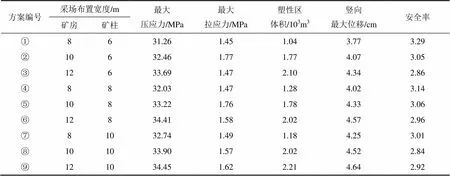
表2 各方案力学响应指标比较
开采所造成的最大拉应力为1.77 MPa,小于围岩的抗拉强度(2.02 MPa),并且各方案的安全率均大于2(破坏准则),说明将开采宽度布置在12 m以内是安全的,验证了力学分析的合理性。归纳出力学响应指标随结构参数的变化规律为:1) 采场最大压(拉)应力分别与矿房宽度和矿柱宽度成正比;2) 塑性区体积与矿房宽度成正比;3) 安全率与矿房宽度成反比。
4 结构参数方案综合分析
开采安全性往往与生产效益相矛盾。当开采结构参数较小时,采场安全性相对较高,但采场生产能力受到限制,生产效率难以提高。故必须在安全和经济之间找到1个平衡点,综合考虑2方面因素,从而确定最佳的开采结构参数。理想点法(TOPSIS)是通过计算评价对象与理想化目标的接近程度,实现多目标决策分析的一种常用方法。这里引入理想点法对各初选方案进行综合评价,步骤如下[13]。
1) 建立初始评价矩阵。综合考虑安全指标和经济指标两大因素。安全指标取数值分析的结果,包括最大压应力(a1)、最大拉应力(a2)、塑性区体积(a3)、竖向最大位移(a4)、安全率(a5)。本着突出重点、易于获取的原则,选取的经济指标为采切比(a6)、采场生产能力(a7)和采充直接成本(a8)。参照矿山实际的生产指标[14],计算获得各组方案的经济评价指标见表3。
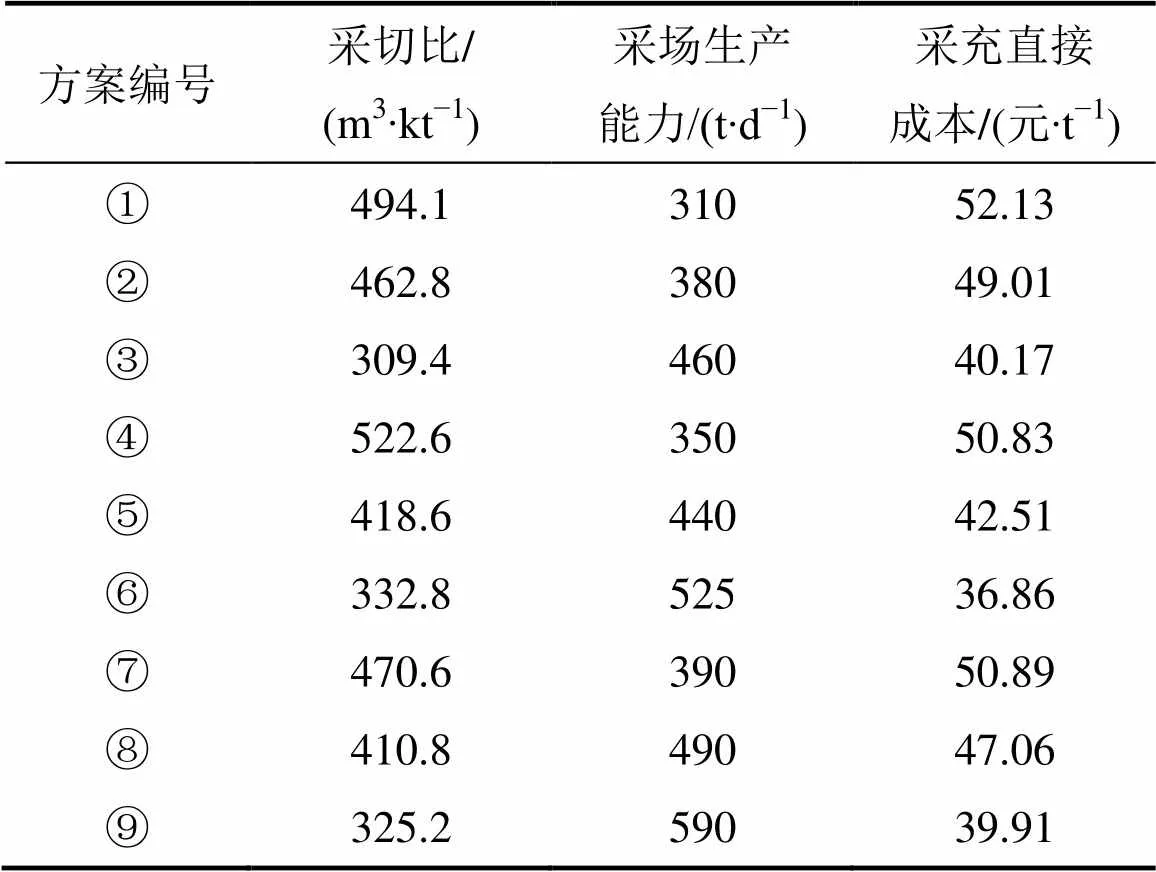
表3 经济评价指标值
建立初始评价矩阵:
式中,A为初选方案的指标向量集,= 9。
2) 规范化评价矩阵。在评价矩阵中,安全率(a5)和采场生产能力(a7)为效益型指标,其取值越大越好;其他各组指标均为成本型指标,其取值越小越好。为便于计算,取a5和a7的倒数为其新的指标取值,统一指标类型,对矩阵进行归一化处理,得到新的评价矩阵:
式中:b为转换后的指标值,=9,=8。
3) 确定正、负理想解。定义各类指标的最小值集合为正理想解(+),最大值集合为负理想解(−),得
4) 向量相似度计算。分别计算各方案评价指标向量集与理想解+和−的距离分别为D+和D−:
由此得到与理想解的向量相似度为
对于成本型指标,T越大,代表其与正理想解的距离越近,与负理想解的距离越远。通过比较各组指标集的T,便可得到方案的优越度排序。
5) 最佳方案确定。方案①~⑨的评价指标集与理想解的向量相似度T依次为0.520 7,0.405 9,0.559 9,0.520 6,0.479 4,0.573 6,0.561 1,0.538 6和0.535 3,因而得到各组方案的优越度排序依次为方案⑥,⑦,③,⑧,⑨,④,①,⑤和②。综上所述,确定方案⑥(矿房宽为12 m、矿柱宽为8 m)为综合考虑安全与经济因素的采场开采最佳结构参数。
6) 工程类比。在实际生产过程中,地下水、应力突变等不可预见因素对开采稳定性的影响较大,受研究手段的约束,尚不能对这类因素予以全面考虑,故参考类似工程条件下某矿山极限开采尺寸[15](矿房宽为18 m、矿柱宽为16 m),方案⑥的取值(矿房宽为12 m,矿柱宽为8 m)均在极限开采尺寸范围之内,可有效规避不可预见因素的影响。
5 结论
1) 通过对采场顶板稳定状态的力学分析,得到顶板受力状态与采场宽度的关系,确定采场安全开采的最大宽度为12.1 m。
2) 采场最大压(拉)应力分别与矿房宽度和矿柱宽度成正比;塑性区体积与矿房宽度成正比;安全率与矿房宽度成反比。单从安全开采的角度而言,方案①(矿房宽为8 m、矿柱宽为6 m)为最佳的开采结构参数方案。
3) 运用多目标决策理想点法综合考虑安全与经济两大因素,通过计算方案评价指标集与理想解的向量相似度,得到初选方案的优越度排序依次为方案⑥,⑦,③,⑧,⑨,④,①,⑤和②。确定方案⑥(矿房宽为12 m、矿柱宽为8 m)为综合考虑安全与经济因素的采场开采最佳结构参数。
[1] 任建平, 阳雨平, 邓良, 等. 国内外倾斜中厚矿体的开采现状和发展趋势[J]. 现代矿业, 2009, 40(6): 1−4. REN Jianping, YANG Yuping, DENG Liang, et al. Present mining situation of inclined medium thickness ore body at home and abroad and development trend[J]. Modern Mining, 2009, 40(6): 1−4.
[2] 罗周全, 管佳林, 冯富康, 等. 盘区隔离矿柱采场结构参数数值优化[J]. 采矿与安全工程学报, 2012, 29(2): 261−264. LUO Zhouquan, GUAN Jialin, FENG Fukang, et al. Stope structural parameters of panel isolation pillar numerical optimization[J]. Journal of Mining & Safety Engineering, 2012, 29(2): 261−264.
[3] 吴爱祥, 武力聪, 刘晓辉, 等. 无底柱分段崩落法结构参数研究[J]. 中南大学学报(自然科学版), 2012, 43(5): 1845−1850. WU Aixiang, WU Licong, LIU Xiaohui, et al. Study on structural parameters of sublevel caving[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1845−1850.
[4] 陶干强, 孙冰, 宋丽霞, 等. 充填法采场结构参数优化设计[J]. 采矿与安全工程学报, 2009, 26(4): 460−464. TAO Ganqiang, SUN Bing, SONG Lixia, et al. Optimal design of stope structural parameters using back-filling method[J]. Journal of Mining & Safety Engineering, 2009, 26(4): 460−464.
[5] 王新民, 李洁慧, 张钦礼, 等. 基于FAHP的采场结构参数优化研究[J]. 中国矿业大学学报, 2010, 39(2): 163−167. WANG Xinmin, LI Jiehui, ZHANG Qinli, et al. Optimizing mining stope structural parameters using a FAHP[J]. Journal of China University of Mining & Technology, 2010, 39(2): 163−167.
[6] 陆广, 罗周全, 刘晓明, 等. 露天转地下开采隔层厚度安全分析[J]. 采矿与安全工程学报, 2011, 28(1): 132−137. LU Guang, LUO Zhouquan, LIU Xiaoming, et al. Safety analysis of interlayer thickness from open pit to underground mining[J]. Journal of Mining & Safety Engineering, 2011, 28(1): 132−137.
[7] 谢承煜, 罗周全, 贾楠, 等. 缓斜极厚矿体开采安全切顶厚度研究[J]. 采矿与安全工程学报, 2013, 30(2): 278−284. XIE Chengyu, LUO Zhouquan, JIA Nan, et al. Safety roof cutting thickness in mining gently inclined and extremely thick ore body[J]. Journal of Mining & Safety Engineering, 2013, 30(2): 278−284.
[8] Grasselli G. 3D Behavior of bolted rock joints: experimental and numerical study[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(1): 13−24.
[9] 罗周全, 吴亚斌, 刘晓明, 等. 基于SURPAC的复杂地质体FLAC3D模型生成技术[J]. 岩土力学, 2008, 29(5): 1334−1338. LUO Zhouquan, WU Yabin, LIU Xiaoming, et al. FLAC3D modeling for complex geologic body based on SURPAC[J]. Rock and Soil Mechanics, 2008, 29(5): 1334−1338.
[10] 袁松, 王峥峥, 周佳媚. 隧道地震动力计算边界取值范围研究[J]. 土木工程学报, 2012, 45(11): 166−172. YUAN Song, WANG Zhengzheng, ZHOU Jiamei. Study on the model boundary determination in tunnel’s earthquake dynamic analysis[J]. China Civil Engineering Journal, 2012, 45(11): 166−172.
[11] 李庶林, 杨念哥. 凡口铅锌矿深部矿床地应力测试[J]. 矿业研究与开发, 2003, 23(4): 15−17. LI Shulin, YANG Niange. Strata stress measurement for the deep ore body in Fankou lead-zinc Mine[J]. Mining Research and Development, 2003, 23(4): 15−17.
[12] 郑磊, 高玉宝. 多空区条件下崩落放顶过程的地压显现与矿柱稳定性研究[J]. 有色金属(矿山部分), 2010, 62(4): 11−14. ZHENG Lei, GAO Yubao. Study of ground pressure appearance and pillars stability in caving mining with multi-mined-out areas[J]. Nonferrous Metals (Mine Section), 2010, 62(4): 11−14.
[13] 陆伟锋, 唐厚兴. 关于多属性决策TOPSIS方法的一种综合改进[J]. 统计与决策, 2012, 67(19): 38−40. LU Weifeng, TANG Houxing. A comprehensive improvement of multi-attribute decision TOPSIS method[J]. Statistics and Decision, 2012, 67(19): 38−40.
[14] 徐海. 地下金属矿山产能优化及开采规划[D]. 长沙: 中南大学资源与安全工程学院, 2012: 55−70. XU Hai. Optimization of productivity and mining planning in underground metal mines[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2012: 55−70.
[15] 唐绍辉, 黄英华, 潘懿. 灾害性群空区深部开采采场结构参数优化研究[J]. 中国矿业, 2009, 18(11): 65−68. TANG Shaohui, HUANG Yinghua, PAN Yi. Study on optimization of stope structure parameters due to disastrous complex group of mined area in deep mining[J]. China Mining Magazine, 2009, 18(11): 65−68.
Optimization of stope width of inclined medium thick ore body
LUO Zhouquan1, WANG Wei1, XIE Chengyu1, JIA Nan1, YAO Shu2,YAN Kejun2, CAO Shengxiang2, XIANG Jun2
(1. School of Resources and Safety Engineering,Central South University,Changsha 410083,China;2. Fankou Lead-Zinc Mine, Shaoguan 512325,China)
Based on the fact that the relationship of roof stress status between stope widths was obtained by elastic mechanics analysis and the stope safe mining maximum width was calculated as 12.1 m, the mining structure parameters primary schemes were put forward combined with the actual mine exploitation condition. The mechanical response characteristics under different structural parameters were obtained by numerical analysis simulation. The safety and economy factors were comprehensively considered by multi-objective decisive TOPSIS (technique for order preference by similarity to an ideal solution) method, the superior orders of schemes were determined by calculating the vector similarity of evaluation indexes set to ideal solution, and ultimately the comprehensive optimization of stope structural parameters was realized. The results show that the maximum pressure (pull) stress during stope excavation is respectively proportional to the chamber and pillar width, the plastic volume is proportional to the chamber width and the safety factor is inversely proportional to the pillar width. The scheme with chamber width 12 m and pillar width 8 m is the optimal stope mining structure parameters which comprehensively consider safety and economy factors.
inclined medium thick ore body; large diameter and deep hole mining method; elastic mechanics; numerical analysis; TOPSIS (technique for order preference by similarity to an ideal solution)
10.11817/j.issn.1672-7207.2015.10.041
TD853
A
1672−7207(2015)10−3865−07
2014−10−12;
2014−12−22
国家自然科学基金资助项目(51274250);国家“十二五”科技支撑计划项目(2012BAK09B02-05);中南大学中央高校基本科研业务费专项资金资助项目(2013zzts057)(Project (51274250) supported by the National Natural Science Foundation of China;Project (2012BAK09B02-05) supported by the National "Twelfth Five-Year" Science and Technology Support Program;Project (2013zzts057) supported by the Business Fee Special Funds of Central University Basic Scientific Research of Central South University)
罗周全,教授,博士生导师,从事金属矿床开采及灾害监控理论与技术研究;E-mail:lzq505@hotmail.com
(编辑 陈灿华)

