基于阈值参数距离的模糊C均值聚类算法及应用

刘敏，杜军

（空军工程大学，西安　710138）

基于阈值参数距离的模糊C均值聚类算法及应用

刘敏，杜军

（空军工程大学，西安710138）

0　引言

纵观人类历史的发展历程，知识总是来自于对自然界和社会中新事物、新现象的认识与研究，分类一直是最原始且最直观的一种认识活动。所谓分类，就是人们为了认知一种新事物或新现象，通过尽可能多的列举其固有属性与特征并在此基础上与已知的其他事物或现象进行比较，以若干既定的标准和规则来衡量新旧事物或现象间的相似性的活动。狭义的聚类分析（或划分）属于硬聚类，其分类规则具有很强的唯一性，即某个对象属于且仅属于某个特定的类，简单而言就是“非此即彼”。但在实际情况中，我们往往无法对事物间纷繁复杂的关系给出确定的度量，即类别界限的划分往往是“模糊”的。1969年，Ruspini最先开始对模糊聚类进行了系统的表述和研究［1］，由此开启了模糊聚类分析的浪潮。

1　模糊C均值聚类（FCM）算法

自从Ruspini提出模糊划分概念并把模糊集理论引入到聚类分析之后，来自世界各地的研究者们在此基础上提出了许多种模糊聚类分析方法，主要包括基于模糊等价关系的传递闭包方法［2-3］、基于相似性关系和模糊关系的方法［4］、模糊图论的最大数方法［5］以及基于数据集的凸分解［6］、动态规划［7］和难以辨识关系等方法。以上几种模糊聚类算法共有的一个弊端是计算非常复杂，应用时往往难以落到实处，而计算量相对简单的基于目标函数的聚类方法开始获得研究者的青睐。在众多基于目标函数的聚类算法中，最典型且应用最广泛的是模糊C均值（FCM）算法。

算法通过最小化基于类内平方误差和（WGSS）范数和聚类原型的目标函数将没有标签的数据进行分类。令X=｛x1，x2，…，xn｝⊂R表示给定的样本集合，s是样本空间的维数，n是样本个数，c（c＞1）是对X进行划分的聚类个数。FCM算法可以描述如下：

上式中：m＞1是模糊系数；U=uij是一个c×n的模糊划分矩阵，uij是第j个样本xj属于第i类的隶属值；V=是由c个聚类中心向量构成的s×c的矩阵；表示从样本点xj到中心点vi的距离，本文采用的是欧氏距离。这是一个关于自变量（U，V）约束优化问题，利用极值点的KT必要条件可以得到如下的迭代方程：

若Ij≠Ø，则uij是满足如下条件的任意非负实数：

2　基于阈值参数距离的模糊C均值聚类（TFCM）算法

在工业领域中，模糊聚类的方法被创造性地应用到故障诊断中。实际的故障模式诊断过程中，我们在模糊聚类分析时通常采用的分类原则是：（1）若待分类样本到各个类的欧氏距离之间差别不大，我们则认为该样本与所有类之间都存在隶属关系，隶属度函数等同于传统的FCM算法；（2）若待分类样本到某几类的欧氏距离相对较小，而到其他若干个类的欧氏距离差别不大，我们则认为该样本与这些类之间都存在隶属关系，且隶属度函与样本和类间的欧氏距离相关联；（3）若待分类样本与某一类的欧氏距离远小于它与其他故障类的距离，我们则认为样本仅属于该类。通过对样本与类间的距离尺度的筛选，使距离类中心比较远的样本点对该类的隶属度为0，这在一定程度上可以剔除样本中的野值，降低样本数据的噪声对聚类结果的不利影响，对算法的鲁棒性也有所改善。大多数可信度较高的样本点的隶属度和样本与类间欧氏距离相关，这也更符合故障分类的实际情况。为了对数据中样本与各聚类中心的欧氏距离差异化处理，我们预先设定一个阈值参数，通过比较欧氏距离与阈值的大小对样本进行初步筛选，根据筛选结果对隶属函数进行调整。为方便起见，我们使用如下的阈值参数距离：

定义如下集合：相对欧氏距离非正的类别集合：

相对欧氏距离为负的类别集合：

相对欧氏距离最小的类别集合：

以下讨论模糊加权指数m在不同范围取值时的算法情况。

（1）当m=1时，算法为传统硬聚类，有划分矩阵

（2）当m＞1时，需要分两种情况讨论：

式（3）最优的一阶必要条件为：

由约束条件有：

解得：

即:

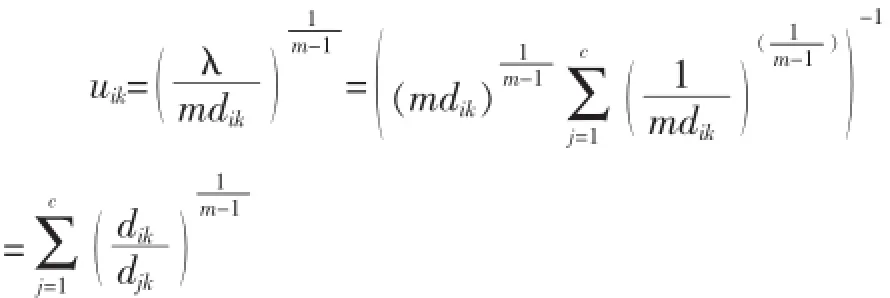
可见，算法为传统FCM算法，有划分矩阵：

②如果NIk≠Ø，则有iNIk，uik=0。式可转化为：

约束条件转化为：

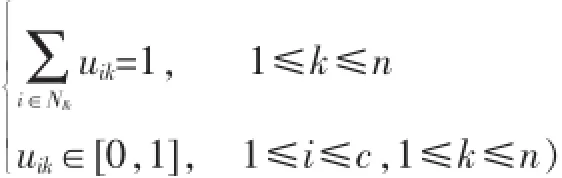
显然，由于m＞1且对i∈NIk，dik≤0，所以是｛uik|i∈NIk｝的凹函数，因此｛uik|i∈NIk｝只能在可行域的边界上取值，且：

可见，当m＞1时，以上两种情况都无法实现半模糊划分。

（3）当0＜m＜1时，也分两种情况讨论：

①如果NIk=Ø，必有dik≥0，1≤i≤c，所以所示的目标函数Jm'是Uk=（u1k，u2k，…，uck）'的凹函数，因此最优解｛uik|i∈NIk｝只能在可行域的边界上取值，且：

②如果Nk≠Ø，则有iNIk，uik=0。上式可转化为：

约束条件转化为：

由于对∀i∈Nk，dik＜0，以及0＜m＜1，所以式是Uk= （u1k，u2k，…，uck）'的凸函数，而约束条件给出的可行域也为凸函数，因此这是一个凸规划问题。可用Lagrange乘子法来求解，引入乘子，并建立Lagrange函数：

其最优的一阶必要条件为：

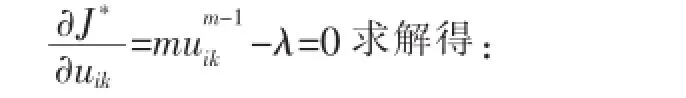
由约束条件有：

解得：

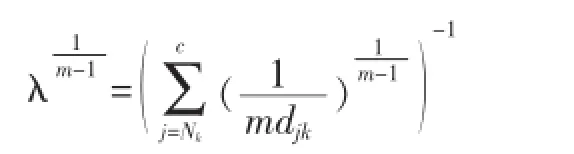
即:

由此可得:

由上式可知，当0＜m＜1时，基于隶属函数的模糊聚类改进算法具有了“半模糊”的特性，具体表现为：样本对其相对欧氏距离的中心点对应的类的隶属度为0，对其相对欧氏距离的中心点对应的类的隶属度互不相同。

TFCM聚类算法的迭代过程简述如下：首先判断一个样本xk与各个类间的相对欧氏距离是否非正，若为正，则样本xk属于与其相对欧氏距离最小的中心点对应的类（即传统的硬聚类）；若为负，则样本xk与此类间都有隶属关系。

迭代目的是寻找一组中心矢量使得类内加权平均误差和函数最小，因此可以将迭代的过程视为目标函数逐渐减小的过程，那么阈值参数η理应随着迭代次数的增加而减小。同时要确保阈值参数η趋近于0，即，这样才能确保得到最终的聚类结果。

对于阈值参数η相对迭代次数的递减方式，我们分别选择平稳下降和凹状递减下降两种方式，其中，平稳递减方式采用正比例下降规律，选取的阈值函数η（t）如下：

令Tmax为算法的最大迭代次数，η（0）为初始阈值，阈值随着迭代递减：

凹状递减方式采用反函数下降规律，选取的阈值函数η（t）如下：

FCM算法目标函数和两种下降方式下阈值参数变化曲线如图1所示。

由图1可以看出，相对当凹状递减方式而言，平稳递减方式阈值参数η下降速度更缓慢。由于迭代初期目标函数随迭代次数的下降速度比平稳递减方式下阈值参数的下降速度快，因此会导致阈值参数距离普遍为负值继而使大量的样本被确定地划分到与其欧氏距离最小的类中，即隶属度函数出现边界分化现象；而凹状递减方式下阈值参数的下降速度始终比目标函数下降速度快，因此可以避免边界分化现象的发生。故而本章中我们对阈值参数η的选取原则是随着迭代次数的增加呈现凹状递减方式。

图1　FCM算法目标函数与两种下降方式下阈值参数变化曲线

3　仿真结果

人工构造一组包含300个样本的数据data_4_1，共分为三类，每类样本数各100个并呈正态分布，分布中心坐标分别为（2，4），（4，2），（3，3）。分别采用FCM算法和TFCM算法的进行分类试验。其中，FCM算法初始化参数为：其中，FCM算法初始化参数为：c=3，m= 2，Tmax=50，TFCM算法初始化参数为：c=3，m=0.7，Tmax= 50，η（0）=1。聚类结果图2所示。

由图2可以看出，FCM与TFCM算法对于人造数据集data_4_1的聚类结果完全一致，但聚类中心位置稍有差异。将两种算法得到的聚类中心与实际聚类中心对比如图2所示，由图2我们可以看出，FCM算法得到的聚类中心相对的实际聚类中心而言更加集中，而TFCM算法得到的聚类中心之间更为分散。这是因为FCM算法对样本与类间的距离不作考虑而进行的无差别分类的结果，但TFCM算法将样本与类间的距离作为隶属度的一个重要的衡量标准，在一定程度上克服了无差别分类带来的盲目性。

FCM算法与TFCM聚类算法的目标函数对比如上图3所示：由图4可以看出，随着迭代次数的增加，目标函数一直下降至迭代阈值，且TFCM算法相比FCM算法收敛速度更快。

我们取用标准数据Iris（鸢尾草植物）作为测试样本集。仿真参数设置如下：FCM算法初始化参数为：c= 3，m=2，Tmax=50，TFCM算法初始化参数为：c=3，m= 0.75，Tmax=50，η（0）=18。聚类结果如表1所示：由表1可以看出，TFCM算法相比较FCM算法而言，其聚类进度和收敛速度更好。

图2　 FCM算法与TFCM算法聚类结果对比

图3　 FCM算法与TFCM算法聚类中心对比　

图4　 FCM算法与TFCM算法聚类目标函数对比

表1数据组的类中心统计结果

4　结语

本文提出了一种基于阈值参数距离的TFCM算法，通过引入阈值参数对样本与类间欧氏距离进行分段使得FCM算法的隶属函数更加合理，数据仿真实验验证了TFCM算法相比较传统的FCM算法具有更好的收敛性与聚类准确性。

［1］Ruspini E H.A new approach to clustering［J］.Information and control，1969，15（1）:22-32.

［2］Dunn J C.A graph theoretic analysis of pattern classification via tamura's fuzzy relation［J］.IEEE Trans.SMC，1974，4（3）:310-313.

［3］Zkim Le.Fuzzy relation compositions and pattern recognition［J］.IEEE Trans.Fuzzy Syst.，1993，1（2）:98-110.

［4］Backer E，Jain A.A clustering performance measure based on fuzzy set decomposition［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1981，PAMI-3（1）:66-75.

［5］Leahy R，Wu Z.An optimal graph theoretic approach to data clustering:theory and it's application to image segmentation［J］.IEEE Trans on PAMI，1993，15（11）:1101-1113.

［6］Esogbue A O.Optimal clustering of fuzzy data via fuzzy dynamic programming［J］.Fuzzy Sets and Systems，1986，（18）:283-298.

［7］Harris J O，Bezdek J C.Convex decompositions of fuzzy partitions［J］.J.Math.Anal.&Appl，1979.

Threshold Parameter；Fuzzy Clustering；FCM；Half Fuzzy

Fuzzy C Means Clustering Algorithm Based on Distance Threshold Parameter and Application

LIU Min，DU Jun
（Air Force Engineering University，Xi'an 710138）

1007-1423（2015）29-0021-06

10.3969/j.issn.1007-1423.2015.29.006

刘敏（1992-），男，安徽合肥人，在读硕士研究生，研究方向为智能检测与健康状态监控

2015-10-09

2015-10-20

针对提出一种基于阈值参数距离的模糊C均值聚类算法，其思想是在对设定阈值参数对样本数据到聚类中心的距离进行分段，距离大于阈值参数的点相对聚类中心的隶属度为0，距离小于阈值参数的点相对聚类中心的隶属度不同且服从特定的隶属函数。理论推导该算法有效时模糊度指数应介于0到1之间，仿真结果表明该算法相比较传统的FCM算法具有更好的收敛性与聚类准确性。

阈值参数；模糊聚类；FCM；半模糊

杜军（1974-），男，山西运城人，博士，教授，研究方向为智能检测与健康状态监控

Presents a kind of fuzzy C Means clustering algorithm based on distance threshold parameter is in.The attach degree of distance greater than the threshold value of the parameter point opposite the center of the cluster will be 0，oppositely belong with an approach function since the distance less than the threshold value of the parameter point opposite the center of the cluster by setting a threshold parameter. Theoretical derivation of the algorithm is effective when ambiguity index should be between 0 and 1.Simulation results show that the algorithm has better convergence and clustering accuracy compared to traditional FCM algorithm.