稀疏控制比例仿射投影算法的正则化参数设计

朱燕红

（浙江广厦建设职业技术学院，东阳　322100）

稀疏控制比例仿射投影算法的正则化参数设计

朱燕红

（浙江广厦建设职业技术学院，东阳322100）

0　引言

当回声路径脉冲响应为稀疏时，采用NLMS算法对回声消除系统中的自适应滤波器系数进行更新时，收敛速度较慢。为了克服NLMS算法的这一局限性，Duttweiler提出了比例归一化最小均方算法（PNLMS）［1］。但当回声路径冲激响应为时变时，PNLMS性能下降明显，为提高算法的鲁棒性，文献［2］通过引入稀疏性系数来调整增益矩阵中比例控制因子，得到了一种稀疏控制IPNLMS算法。但当输入为语音信号时，稀疏控制IPNLMS算法的收敛速度明显下降。为此文献［3］提出了重复利用过去的输入信号来提高自适应滤波器收敛速率的稀疏控制比例仿射投影算法（SC-IPAPA）。

在稀疏控制比例仿射投影算法中，为了克服数值计算困难，需要使用正则化参数。此外，在SC-IPAPA中，存在着收敛速度和稳态失调之间的矛盾，当选择较大的步长或很小的正则化参数时，SC-IPAPA算法收敛较快，但其稳态失调较高；反之，若选择较小的步长或较大的正则化参数时，SC-IPAPA算法的稳态失调较低，但其收敛较慢。文献［4］提出的采用变步长参数的分割式比例仿射投影算法（VSS-SPAPA）解决了SC-IPAPA算法中存在的收敛速度和稳态失调之间的矛盾，但VSS-SPAPA算法中必须使用正则化参数，其正则化参数是预先设定的，对于时变的噪声环境，影响了算法的收敛速度和稳态性能。基于此考虑，本文通过迫使后验误差功率等于系统噪声功率，提出了变正则化参数的SC-IPAPA算法（VR-SC-IPAPA）。

1　稀疏控制IPAPA算法（SC-IPAPA）

考虑时刻k的如下线性模型：

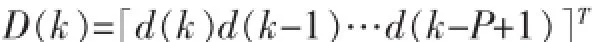
于是SC-IPAPA的系数更新过程可表示为［3］：

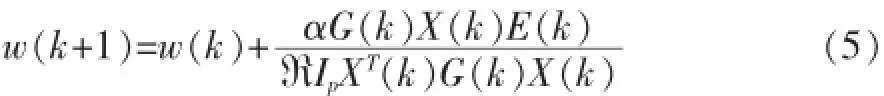
其中：α是整体步长参数；R为正则化参数［5］；步长控制矩阵G（k）=diag｛g1（k）g2（k）… gN（k）｝是一个对角矩阵，用来调整滤波器每个系数对应的步长，增加活动系数的收敛速度。SC-IPAPA算法中gn（k）的递推计算可归纳为：

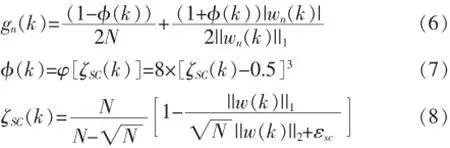
2　变正则化参数SC-IPAPA算法（VRSC-IPAPA）

对固定步长α和固定正则化参数R的SC-IPAPA算法，快速收敛与低稳态失调这两个需求是互相矛盾的；选择较小的R和较大的α能加快算法的收敛速度，但会导致较大的稳态失调；反之，较大的R和较小的α能获得较小的稳态失调，但是收敛速度也会相应变慢。但变步长参数算法中需要采用正则化参数来克服数值计算困难，且其正则化参数不能随系统噪声功率大小进行自适应调节。因此，本文采用优化正则化参数来解决SC-IPAPA算法中快速收敛与低稳态失调之间的矛盾。

对于SC-IPAPA算法，在存在系统噪声的情况下令ε（k）=0，会在w（k+1）中引入噪声的影响，合理的方法是令：

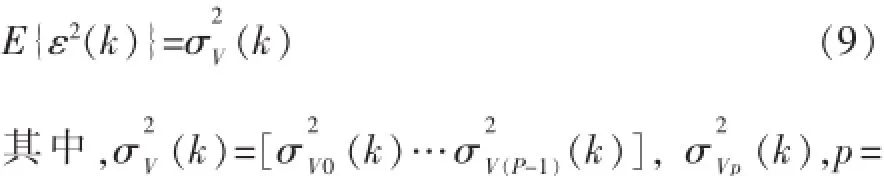
0，1，…，P－1为干扰信号v（k-p）的方差。令式（5）中α= 1，并用变正则化参数构成的对角矩阵Rap（k）=diag｛R0（k），R1（k），…，RP－1（k）｝替代RIP，可得变正则化参数SC-IPAPA算法如下：

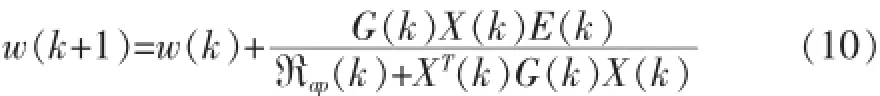
将其代入式（4），并结合式（2）、（3）有：

此外，对高阶自适应滤波器而言，可认为：

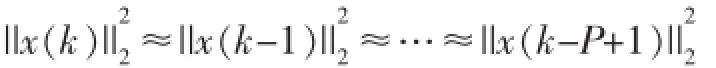
结合式（6），可得：

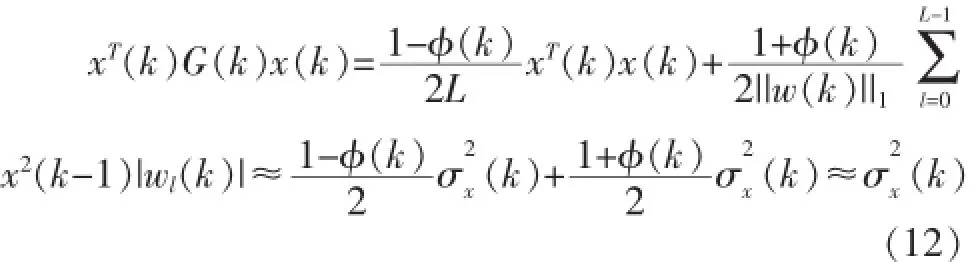
结合式（11）、（12），可得：

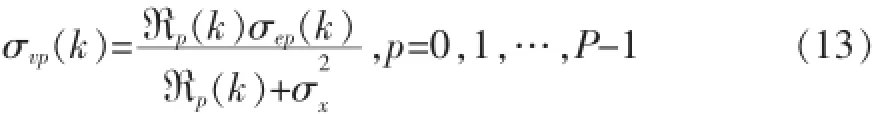
上式经整理后，可得：

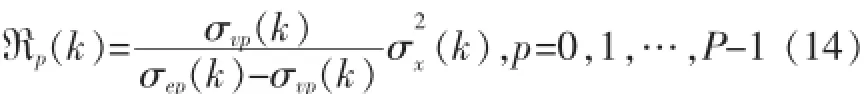
上式中 σvp（k）在语音停顿间获得，而、σep（k）用指数窗方法对其进行估计。当时，Rp（k）将为负值，因此当时，令 Rp（k）等于Rp（k-1）。同时为防止式（10）被零整除，可设置Rp（0）为一个小的正数τ。于是可得Rp（k），p=0，1，…，P-1：

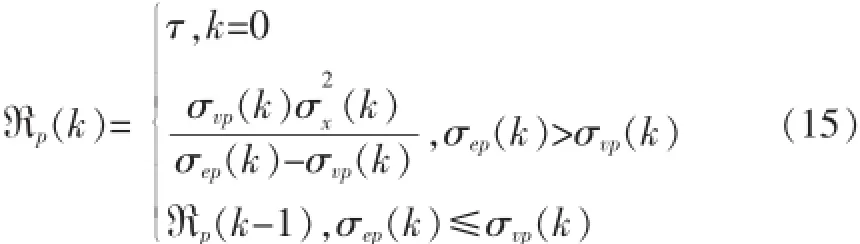
3　仿真分析

仿真试验比较了文献［3］（2009）所提的SC-IPAPA （P=2）、文献［4］（2009）提出的变步长比例仿射投影算法（VSS-SPAPA，P=2）、文献［5］（2010）提出的变正则化参数仿射投影算法（VR-APA，P=2）与本文新算法（VRSC-IPAPA，）的性能。仿真试验中使用有色信号作为滤波器的输入；期望信号由输入信号通过回声路径再迭加上与输入信号独立的白高斯观测噪声v（k）得到，VSS-SPAPA算法中R=Pσ2x（k），SC-IPAPA算法中分别取100和10-10，SC-IPAPA算法中步长 α=0.8，VR-APA算法和VR-SC-IPAPA中步长α=1.0，采用归一化失调误差作为性能比较标准，其定义为：

图1比较了新算法和相关算法的收敛和稳态性能，信噪比（SNR）为10dB，从图1中可看出，VR-SC-IPAPA与SC-IPAPA（R=10-10）有相同的初始收敛速度，但其稳态失调有约22dB（SNR=10dB）的改善。对于SC-IPAPA，要获得与VR-SC-IPAPA相近的稳态失调，正则化参数R必须大于100，但此时收敛速度变得十分缓慢。在相同的P值下，与VR-APA相比稳态性能和收敛速度都得到了提高。

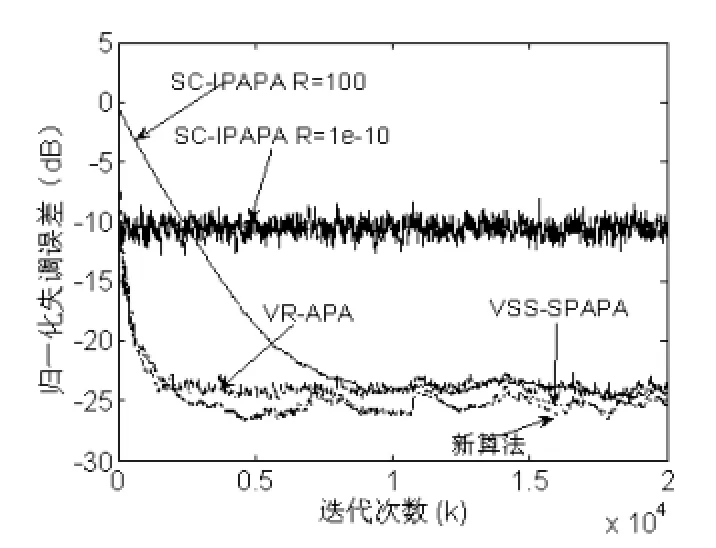
图1　新算法与相关算法收敛性能比较（输入为有色信号，SNR=10dB）

5　结语

本文提出的正则化参数随噪声功率大小进行自适应调节的稀疏控制比例仿射投影算法，在解决快速收敛和稳态失调之间矛盾的同时，克服了正则化参数最优值的选取问题。理论分析和仿真结果表明：由于新算法中的正则化参数能随噪声功率大小进行自适应调节，较已有的变步长比例仿射投影算法，当信噪比增加或发生变化时，新算法具有更好的收敛和跟踪性能。

［1］Duttweiler D L.Proportionate normalized least-mean-squares adaptation in echo cancellers［J］.IEEE Trans.Speech Audio Process.，2000，8（5）：508-518.

［2］Andy W H，Khong，Patrick A.Efficient use of sparse adaptive filters signals［J］.System and Computers，2006，10（6）：1375-1379.

［3］LIU，Li-gang.On improvement of proportionate adaptive algorithms for sparse impulse response［D］.Kochi，Japan：Kochi University of Technology，2009.

［4］LIU Li-gang，Masahiro Fukumoto，Sachio Saiki，et al..A variable step-size proportionate affine projection algorithm for identification of sparse impulse pesponse［C］.Proc.the 16th International Conference on Digital Signal Processing（DSP2009），Aegean island of Santorini，Greece，2009（2）：1-6.

［5］Yin，W.，Mehr，A.S.A variable regularization method for affine projection algorithm［J］.IEEE Trans Circuits System II：Express Briefs，2010，57（6）：476-480.

Echo Cancellation；Regularization Parameter；Sparseness-Controlled；Proportionate Affine Projection Algorithm

Regularization Parameter Design of Sparseness-Controlled Proportionate Affine Projection Algorithm

ZHU Yan-hong
（Vocational College of Zhejiang Guangsha Construction，Dongyang 322100）

1007-1423（2015）20-0003-04

10.3969/j.issn.1007-1423.2015.20.001

朱燕红（1974-），女，浙江兰溪人，工程硕士，讲师，研究方向为计算机应用、信息处理2015-04-03

2015-07-02

针对稀疏控制比例仿射投影算法收敛速度和稳态失调之间的矛盾及正则化参数最优值难以确定的问题，通过迫使后验误差功率等于系统噪声功率，提出一种正则化参数随噪声功率大小进行自适应调节的稀疏控制比例仿射投影算法。算法解决稀疏控制比例仿射投影算法中正则化参数最优值的选取问题及快速收敛和稳态失调之间的矛盾。仿真结果验证所提算法的有效性。

回声消除；正则化参数；稀疏控制；比例仿射投影算法

In various noise environments，the regularization parameter of the sparseness-controlled improved proportionate affine projection algorithms is difficult to be determined.To address the problem，proposes a variable regularization adaptive filtering algorithm by setting the component of the posterior error energy vector to equal that of the noise variance，termed VR-SC-IPAPA.The computer simulation results verify that the proposed algorithm with a negligible additional computational cost can solve the problem of trade-off between convergence rate and steady-state misalignment and improve the performance of the SC-IPAPA.