汽车ABS系统智能滑模控制器的研究与设计
陈德海,付长胜,王一栋(江西理工大学电气工程与自动化学院,江西 赣州 341000)
汽车ABS系统智能滑模控制器的研究与设计
陈德海,付长胜,王一栋
(江西理工大学电气工程与自动化学院,江西 赣州 341000)
文章首先分析了车辆制动系统的主要结构,并建立了其主要功能模块的数学模型;而后在对系统可观测性论证的基础上,将神经网络理论方法和滑模控制理论方法相融合,设计一种基于滑移率的智能滑模控制器,提出了车轮最佳滑移率的离线辨识方法;并将智能滑模控制器和最佳滑移率的离线辨识方法应用于改善车辆ABS系统刹车性能,提高安全控制效果上。对单轮系统车辆的仿真表明:所设计的控制器控制效果具有较强的鲁棒性,无论何种路面车速如何相对于普通的滑模控制器,该智能滑模控制器都能更好地控制车辆使滑移率保持在更佳的数值,从而提高了制动效率,缩短了刹车时间缩小了制动距离。
滑移率;滑模控制;制动系统;智能滑模控制器
10.16638/j.cnki.1671-7988.2015.12.002
CLC NO.: TP391.9Document Code: AArticle ID: 1671-7988(2015)12-03-05
引言
车辆能否安全稳定的驾驶在很大程度上取决于车辆ABS系统,它对车辆的安全行驶起着关键性作用。目前适用范围比较广泛,应用比较成熟的控制理论方法主要有逻辑门限值控制、最优控制和变结构控制等。逻辑门限值控制的门限值必须要经过多次试验才能确定,无法对系统稳定性品质进行评价,控制过程不稳定。对ABS这种具有明显非线性和不确定性的系统,有必要采用一种高鲁棒性的非线性控制器来加以控制。滑模控制[1-3]是一种重要的高鲁棒控制理论和方法,它能使非线性系统相对保持稳定并且能消除模型中的不确定性。本研究中用神经网络控制理论与滑模控制理论相融合,研究并完成一种智能滑模控制器,并且用边界层方法消除颤动现象。
1、制动过程模型建立
1.1单轮车辆制动模型
本研究目的是对汽车ABS系统的功能进行研究,并探讨汽车ABS系统的控制策略问题,主要涉及车辆的刹车距离、刹车时间、刹车减速度等方面。当汽车行驶过程中突然进行刹车,在刹车过程开始前车轮速度等于汽车行驶速度;刹车过程中,车轮速度小于汽车行驶速度速度。刹车时,作用在车轮上的力矩有两个:一是刹车动盘与静盘摩擦产生的刹车力矩Tb,其方向与车轮转动方向相反;另一个是路面与车轮轮胎的摩擦力Fz产生的力矩,其作用是使车轮转速增加车辆行驶速度减小。如图1所示。
根据牛顿定理有:

公式中,J表示轮胎转动惯量,ω表示轮胎角速度,v表示车辆速度,R表示轮胎滚动半径,Ff表示轮胎与地面之间的摩擦力,Tb表示动力矩,m表示车的总质量的 1/4,Fz表示路面对轮胎的反作用力。

图1 1/4车辆模型
1.2制动执行器模型
制动执行器模型主要包括无刷直流电机模型、电机驱动器模型、传动装置模型和制动器模型等。
1.2.1电机模型[4-5]
当汽车制动时,电机工作状态要经过消除间隙、堵转状态和恢复间隙三个阶段。仅第二种状态时电机会产生堵转力矩。通过减速机构和滚珠丝杠副,最后形成制动压力产生制动力矩,在这时需要进行力矩控制。连续堵转的转矩公式为:

其中,TH表示连续堵转转矩;9.55为功率、转矩转换常数;Ke表示反电势系数;Ik表示连续堵转电流;U0表示空载电压;I0表示空载电流;Ra表示电枢电阻;n0表示空载转速。

表1 电机参数Table 1 Motor parameters
1.2.2传动机构及制动器
传动机构由行星减速机构和滚珠丝杠副构成:

其中,N为输出推力;ηs为传动效率;Ph为丝杠导程。TX为输出转矩;i为传动比;ηX为机械效率。制动力矩为:

其中,kp为制动因数。
将公式(2)(4)和(5)代入(6)可以得到制动执行器的数学模型;
1.3轮胎模型[6-9]
LuGre模型是法国学者Canudas de Wit在基于鬃毛的平均变形下对轮胎建模,属于轮胎物理模型,模型的表达式为[10]:

其中,
式中,μ为摩擦系数;vr为相对滑移速度;vs为特征速度;z为刷毛的平均变形量;g(vr)为Stribeck效应函数:α0、α1分别为刷毛的刚度参数和阻尼参数;σ0、σ1为摩擦系数参数;σ2为粘性摩擦参数。
每种道路都有不同的滑移率附着系数曲线,当道路条件不同时,道路滑移率附着系数曲线是不相同的,其峰值所对应着的道路最佳滑移率也都不相同的,它的值是动态变化的。因此,为了能够更好地仿真本论文采用离线的方法计算出路面的最优滑移率,在仿真过程中智能滑模控制器的最优滑移率是通过查表方的式得出的,该表的输入参数是车辆速度和路况参数,最优滑移率是用LuGre模型计算出来的。
2、智能滑模控制器设计
2.1滑模控制方法
考虑单输入动态系统:

为了既好又快的实现跟踪,设:

根据以上叙述知,跟踪误差向量:

在状态空间 Rn中时变滑模面用标量 s(x,t )=0定义:

其中,α>0。当n=2时,有

即s是误差及其导数的线性组合。
给定初始状态(10),当t>0时跟踪任务轨线必须保持在滑模面 S(t)上。所以,可以把跟踪向量 xd的任务可转化为标量s≡0的问题来处理。
李雅普诺夫泛函 V(t)∈ R+定义为:

通过设计u,使即使在滑模面 S(t)以外也可以满足可达性条件:

其中η>0。实际上,式(16)说明了轨线趋向于滑模面 S(t)
选择合适的控制律u使s2是李雅谱诺夫泛函。设计控制器的过程共分为两步:1)设计控制律u使得可达性条件;(15)得到满足;2)消弱抖振现象。
2.2滑模控制器设计
1/4车辆动力学的公式结合(7)可得:

滑移率λ对时间求导,得:

为了用滑模控制器控制车辆 ABS系统,通过调节电流Ik的值,使得误差λd-λ趋近于零,其中,λd为道路最优滑移率,通过离线查表方法获得。定义滑模面为:

在这里e=λd-λ,b表示待设计的正常量,选择n=1则

则滑模面的可达条件为:

式中,η为正数。
2.2.1等效控制量及切换控制量设计
将式(16)代入式(17),得

尽管μB的准确值很难获取,但是只要

就能够设计出鲁棒性很强的滑模控制器。
对(19)进行求导,得

令s.=0即可得等
因为系统中有很多不确定性因素和外界的干扰,因此需加入切换控制,即使系统对不确定性因素和外界干扰具有鲁棒性。
将(23)代入(20),得

若令

则(25)可改写为

当s≥0时,要确保满足可达性条件,满足

即可,所以设计

当s<0时,(29)也适用。
将(29)代入(26)得

2.2.2抖振现象抑制
通常削弱抖振的方法有分两类[11]:(1)用饱和函数代替符号函数;(2)插入边界层,当系统进入边界层时,用等效控制代替相应控制。因为当采用第二种方法时经常存在静态误差,所以大多数用饱和函数和S函数代替符号函数。本文用Ambrosioe函数:

消弱抖振。因此,上文设计的控制律(31)最终为:

公式(32)即为滑模控制器。
2.2.3智能滑模控制设计[12]
通过公式(32)可得,滑模控制共有两个部分构成,他们分别是等效控制量与切换控制量,因为后者有不连续性,所以经常导致抖振的产生。为减小抖振使系统能够根据输入量自动调节切换控制量的大小,在智能滑模控制器的研究设计中用BP神经网络滑模校正器替代切换控制量。BP神经网络校正器设计如下。
由滑模控制理论可知系统运动点沿着切换平面做滑模运动与滑模误差函数s及其变化率有关。根据控制器校正器的输入输出个数和控制精度的要求,选择双输入单输出控制器。输入为误差s及误差变化率s.,输出为切换控制量us。因此建立一个具有两个输入节点,一个隐含层具有两个节点,和输出层具有一个节点的BP神经网络。其BP神经网络控制图如图2。

图2 BP神经网络控制图Fig.2 BP neural network Controller
隐含层的加权系数及偏置的初始值为:

(2)计算样本集中所有样本的隐含层和输出层各节点的输出值,即
隐含层第1个神经元的输出为:

隐含层第2个神经元的输出为:
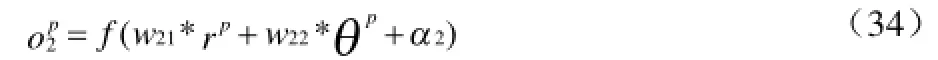
输出层神经元的输出为:

(3)计算在所有样本作用下的各层误差,即输出层的误差为:

隐含层第1个神经元的误差为:

隐含层第2个神经元的误差为:

(4)调整各层的加权系数及偏置,即输出层的加权系数及阈值修正公式为:

隐含层的加权系数及阈值修正公式:

(5)计算输出误差:
根据上述的神经网络,来简单介绍BP神经网络的算法。
(1)置所有的隐含层的加权系数及偏置的初始值为最小的随机数

存在一个ε>0,使得J<ε,否则返回调整权值,重新计算,
BP神经网络学习算法有离线学习(批处理)和在线学习两种。所得的权值修正是在所有样本输入后,计算完总的误差后进行的,这种修正称为离线学习。离线学习修正可保证其总误差J向减少的方向 变化,在样本多的时候,它比处理时的收敛速度快。在线学习是对训练集内每个模式对逐一更新网络权值的一种学习方式,其特点是学习过程中需要较少的存储单元,但有时会增加网络的整体输出误差。上述学习算法就是在线学习过程。因此使用在线学习时一般使学习因子足够小,以保证训练集内每个模式训练一次后,权值的总体变化充分接近于最快速下降。
3、控制器的仿真[13]
3.1模块模型
最优滑移率辨识模型如图3所示,输入为路面条件系数与车速,输出为最优滑移率。
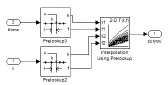
图3 最优滑移率辨识模型Fig.3 Optimal slip rate identification model
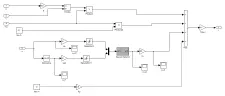
图4 智能滑模控制器模型Fig.4 Intelligent sliding mode controller model
3.2仿真结果
选用智能滑模控制器的车辆ABS系统仿真结果如图5、6、7所示:

图5 固定滑移率仿真结果Fig.5 Results of fixed slip rate simulation
由图5、6和图7知,无论是在固定滑移率、最优滑移率情况下,还是在路面突变情况下,选用普通滑模控制器和智能滑模控制器汽车 ABS系统都能很好地根据最优滑移率变化而时刻调整滑移率,但是用智能滑模控制器的车辆 ABS系统要比用普通滑模控制器的车辆ABS系统制动性能更好,能够使系统在更短时间内达到最优滑移率使系统稳定性更好。与普通滑模控制器相比智能滑模控制器的响应更加灵敏、控制精度更高,因此刹车时间与刹车距离都更短,使刹车过程中车身更加平稳。

图6 最优滑移率仿真结果Fig.6 Simulation results of optimal slip ratio

图7 路面突变最优滑移率仿真结果Fig.7 Simulation results of optimal slip ratio of pavement
[1] 胡跃明.变结构控制理论与应用[M].北京:科学出版社,2003.
[2] 王丰尧.滑模变结构控制[M].北京:机械工业出版社,1998.
[3] 周其节.变结构系统[M].广州:华南理工大学出版社,1989.
[4] 陈昌荣.基于滑移率的车辆线控制动系统ABS控制研究[D].湖南大学2010-04-12.
[5] 沈沉,王军,林逸.电子机械制动系统制动执行器建模与试验[J].农业机械学报,2007,38(08):30-33.
[6] 危银涛,冯希金,冯启章,刘源,何园.轮胎动态模型研究的进展[J].汽车安全与节能学报,2014(04):311-323.
[7] 韩继光.车辆 ABS系统最大纵向附着系数估计算法研究[D].昆明理工大学,2007.
[8] 温兴清.基于动态摩擦模型的路面辨识及最优刹车控制研究[D].中南大学,2008.
[9] 庄继德.汽车轮胎学[M].北京:北京理工大学出版社,1995.
[10] Canudas de Wit C.01sson H.,Astrom K.J.,et a1.A new model for control of systems with friction.IEEE Transactions On Automatic Control,1995,40(3):419.425.
[11] J.-J.Slotine,W.Li.Applied Nonlinear Contr01.Prentice-Hall,1991.
[12] 蒋克荣,王治森,孙骏.汽车ABS轮速信号处理过程的神经网络模型[J].农业机械学报.2008-01.
[13] 张长冲.ESP一汽车电子稳定系统仿真研究[C].济南:山东大学机械工程学院,2007-9-10.
Study and Design of Vehicle ABS Intelligent Sliding Mode Controller
Chen Dehai, Fu Changsheng, Wang Yidong
( School of electrical engineering and automation, Jiangxi University of Science and Technology, Jiangxi Ganzhou 341000 )
In this paper, we analyzes the main structure of the vehicle braking system, and set up a mathematical model for its main modules. And then we design an intelligent sliding mode controller based on slip ratio through the integration of neural network theory and sliding mode control theory , based on the demonstration of system observations .In this paperwe propose an offline identification method of optimal wheel slip ratio, and in order to enhance the security control effect, we use intelligent sliding mode controller and optimum slip offline identification method to improve the braking performance of the vehicle ABS system. The simulation of a single wheel vehicle system shows that the controller we designed has strong robustness effect, it can increase braking efficiency, shorten the braking time and reduce the braking distance, for compared with normal sliding mode controller, intelligent sliding mode controller can control the vehicle better and make the slip rate remain at a better value, no matter how uneven the road is, and what speed the vehicle is at.
Slip rate;Sliding mode control; Vehicle ABS; Intelligent sliding mode controller
TP391.9
A
1671-7988(2015)12-03-05
陈德海,副教授,硕士研究生导师,就职于江西理工大学电气工程与自动化学院,主要研究领域为控制理论与工程、汽车电子、自动控制。王一栋,硕士研究生,就职于江西理工大学电气工程与自动化学院,主要从事控制工程、汽车电子方向的研究。
江西省自然科学基金(20151BAB206034)。

