基于HyperWorks的某重型卡车板簧支架轻量化设计

晏全周

前言

板簧支架是重型卡车连接车架与钢板弹簧的重要零部件，其承受来自钢板弹簧的复杂的作用力。在汽车设计中板簧支架作为 A类件（最重要的零部件类），设计时对其强度有着较高的要求。而随着近年来全国各地限超限载政策法规的出台，以及国家对整车质量与公告法规一致性的检查，车辆零部件的轻量化越来越受到主机厂以及用户的重视。重型卡车上板簧支架在设计初期要求在满足强度的前提下减少其自身重量，以满足强度和轻量化需求。

本文以某重型轻量化牵引车板簧支架为优化设计对象，应用CAE分析软件HyperWorks平台中的OptiStuct模板，利用拓扑优化技术，模拟板簧支架受力工况，得到拓扑骨架模型，从而建立板簧支架的优化模型，根据优化结果对板簧支架进行重新设计，并对优化设计合理性进行反向有限元分析验证，在满足强度要求的同时达到减重的目标。

1、拓扑优化设计方法

1.1 变密度法

拓扑优化是一种根据设定载荷、约束条件以及优化目标而寻求结构材料的最合理分布的一种方法。拓扑优化之前需进行三要素设定：设计变量、目标函数和约束条件。对于常用的连续体结构拓扑优化，具体实施方法有均匀法、变密度法、渐进结构优化法等。

变密度法是拓扑优化设计中常用的方法，其采用材料属性描述方式，其基本思想是引入一种假想的密度可变材料，建立物理参数（例如弹性模量、泊松比、许用应力等）与材料的密度之间的关系。对结构进行有限元划分为单元之后，每个独立的单元密度是相同的。进行拓扑优化分析时，设计变量定义为材料的密度，因此将连续体结构的拓扑优化问题转化为材料最优分布问题。基于变密度法，材料的性能和材料的密度成正比。

变密度法中，设计变量为每个单元材料的密度，单元的密度在0到1之间连续变化。单元密度为0时，则代表这个单元密度为空，单元密度为1时，则代表这个段元密度为实，当单元密度为0到1的中间值时，则代表这个单元为假想材料的密度值。将连续结构体离散为有限元模型后，以每个单元的密度为设计变量，将结构的拓扑优化问题转化为单元材料的最优分布问题。

1.2 拓扑优化的数学模型

若以结构变形能最小为目标，考虑材料体积约束(质量约束)和结构的平衡，则拓扑优化的数学模型为：

求X={ X 1，X2，···Xn}T，使得

其中 0 ≤X min ≤Xi≤Xmax

式中， Xi{i =1,2,···,n}——设计变量；

C——为结构变性能；

F——载荷矢量；

U——位移矢量；

f——剩余材料百分比；

V——结构充满材料的体积；

V0——结构设计域的体积；

V1——单元密度小于Xmax的材料体积；

Xmin——单元相对密度的下限；

Xmax——单元相对密度的上限；

K——刚度矩阵。

在多工况的情况下，对各个子工况的变形能进行加权求和，目标函数变化为：

式中，Wi为第i个子工况的加权系数，Ci为第i个子工况的变形能。

2、板簧支架拓扑优化步骤

2.1 有限元建模、约束与加载

运用三维制图软件 CATIA建立板簧支架三维实体模型（如图1所示），在HyperWorks平台的Hypermesh软件中建立三维实体的有限元模型，模型采用四面体单元网格，单元网格大小为3mm，计算时设定弹性模量 E =2. 1×105MPa，泊松比μ=0.3，材料为QT450-10，有限元模型如图2所示。

板簧支架与车架连接分别为与车架覆面的三个螺栓连接和车架下翼面的两个螺栓连接，因此对于有限元模型的约束主要建立如下约束条件，如图3所示：

（1）与车架连接的配合孔约束全部自由度；

（2）与车架覆面连接的三个孔的凸台面约束 X方向的位移以及绕Y轴和Z轴的旋转；

（3）与车架下翼面连接的两个孔的凸台面约束 Z方向的位移以及绕X轴和Y轴的旋转。

在车辆行驶过程中，板簧支架受力较为复杂，在设计计算时选择与板簧支架破坏形式最为密切，关系最大，最具典型性的载荷（简称计算载荷）为依据进行分析计算。加载在板簧支架上的载荷主要有以下几种：

（1）竖直向上的承载载荷，设定载荷为 FZ= 2 .5F0；

车辆紧急制动时朝前的制动载荷或者车辆启动时朝后的惯性载荷，设定载荷为 FY= 2 .0F0；

车辆转弯时所承受的转向载荷，设定载荷为 Fz= 1 .3F0。

因此分析板簧支架受力综合上述三种载荷，总共对六种工况进行强度分析，分别为：

Ⅰ：沿Z轴方向的重载垂直载荷；

Ⅱ：沿Y轴方向的制动载荷；

Ⅲ：沿X轴方向的转弯载荷；

Ⅳ：沿Z轴方向的重载载荷和沿Y轴方向的制动载荷的综合载荷；

Ⅴ：沿Z轴方向的重载载荷和沿X轴方向的转弯载荷的综合载荷；

Ⅵ：沿Z轴方向的重载载荷、沿Y轴方向的制动载荷和X轴方向的转弯载荷的综合载荷。

按照上述六中工况分别对板簧支架加载，所得应力值和安全系数如表1所示：

表1 板簧支架应力值及安全系数

由上述分析结果可以看出，所选定的板簧支架的强度满足设计要求，且有较高的安全系数。需要在满足强度要求的基础上对该板簧支架进行轻量化设计。

2.2 板簧支架优化空间的设定

用Optistruct对原板簧支架进行拓扑优化。将板簧支架的安装孔区域作为不可拓扑空间，保证优化后的模型仍具有装配功能。根据板簧支架拓扑优化的实际需要，结合图5中的分析结果，定义其可优化空间和不可优化空间，由于各安装孔是用来固定支架的，位置和形状基本不变，为不可优化空间，即图中黄色区域显示的部分。可拓扑空间除安装孔以外的部分，即图中绿色区域显示的部分，如图6所示。

2.3 网格划分

通过HyperMesh中的三维网格划分模块对模型进行相关设置并进行四面体网格划分。将模型进行网格划分成四面体单元。对板簧支架模型的拓扑优化在可优化区域内进行。

2.4 建立有限元分析模型

按照3.1对图7中的有限元建模，建立相同约束和载荷。然后通过定义目标函数、约束条件和设计变量进行求解，得到如图9所示的拓扑骨架模型。

综合考虑板簧支架的工艺性、可装配性及拓扑优化结果，将支架形状进行优化，优化后的板簧支架如图10所示。优化前板簧支架重量为5.4kg，优化后该板簧支架重量为4.3kg，实现单个支架降重20.4%。

2.5 拓扑优化结果验证

拓扑优化后得到新的支架模型，为了保证新的支架能够满足结构强度要求，按照上述六种工况进行有限元分析，得到相应的应力值，见表2。

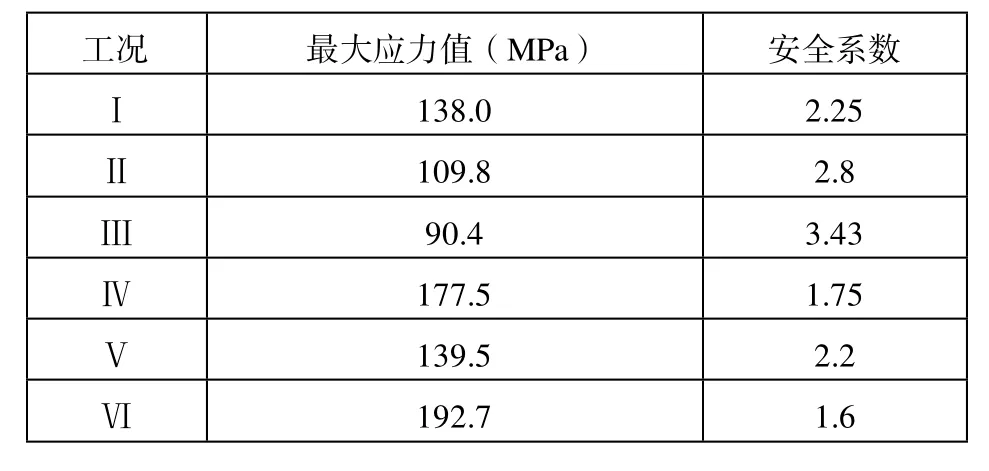
表2 优化后板簧支架应力值及安全系数

从上述分析结果可以看到，该板簧支架应力分布有一定的变化，应力分布更加均匀也更加合理，且从结果对比分析，优化后的应力值较优化前有明显的改善，优化后的结果满足强度要求和实际使用工况。

3、结论

本文以某重型车板簧支架为设计优化对象，基于变密度法建立了拓扑优化的数学模型，并对多工况下的板簧支架结构进行优化设计。根据拓扑优化的结果，结合制造工艺以及设计经验，对板簧支架进行重新设计，最后对新支架结构进行有限元强度验算。结果显示，拓扑优化后的板簧支架，强度比优化前好，安全系数更高，同时重量降低了20.4%。

拓扑优化设计时产品的初步优化设计，要完成板簧支架的完整优化设计，还要做进一步的形貌和尺寸优化，对设计进行细化，这种设计思路可以为其他产品结构设计所借鉴。

[1] 张胜兰,郑东黎等.基于 HyperWorks的结构优化设计技术[M].机械工业出版社,2007.

[2] 吴仕赋．基于有限元汽车支架有限元设计．吉林大学，2005.

[3] 王春会．连续体结构拓扑优化设计[D]．西北工业大学,2005.

[4] 培龙，陆晓黎等．汽车动力总成悬置骨架的拓扑优化设计[J].噪声与振动控制，2010(12):83-87.

[5] 赵永辉，马力，王元良等．自卸车举升机构三角臂拓扑优化设计[J]．专用汽车，2007(9):33-34.