非局域非线性介质中厄米高斯光束的变分解

白东峰　王毅　卢宏炎

摘要： 非局域非线性介质中的薛定谔方程很难用传统的方法得出精确解析解，利用变分法系统研究了强非局域非线性介质中厄米高斯光束的传输问题。通过对非线性介质中响应函数的展开，使得非线性薛定谔方程得以简化，求解出高阶高斯光束孤子解。利用数值模拟研究了厄米高斯光束在介质中传输时束宽不变的问题，结果显示当非局域程度非常大时，解析解非常接近数值解。

关键词： 非局域非线性介质； 变分法； 孤子

中图分类号： O 437 文献标志码： A doi： 10.3969/j.issn.1005-5630.2015.04.005

Abstract： It is difficult to use the conventional method to obtain accurate analytical solution of the Schrodinger equation in the nonlocal nonlinear media. The propagation of Hermite-Gaussian （HG） beams in the strongly nonlocal nonolinear media is discussed with a variational method in this paper. The nonlinear Schrodinger equation can be simplified through expanding the response function in the nonlinear medium. The solution of high-order Gaussian beam soliton is obtained. The beam width of HG beam is unchanged when it propagates in the media by using numerical simulations. The results show that the analytical solution is closer to the numerical solution when the degree of the nonlocality is very large.

Keywords： nonlocal nonlinear media； variational approach； solitons

引 言

空间光孤子是指在介质里面传输时其束宽不变的光束，近年来由于其独特的传输特性在世界范围内引起了极大的关注[1-16]。Snyder和 Mitchell的研究引起了广泛的关注[1]。 Guo等研究了非局域非线性薛定谔方程揭示了高斯孤子的大相移[7]。Huang等利用变分法研究了亚强非局域介质中的光束传输问题[8]。Hu等讨论了向列相液晶中非局域孤子的相互作用[9]。Deng等也得到了拉盖尔高斯光束的讨论并且获得了精确解析解[11]。Bai等利用变分法讨论了非局域非线性介质中的高斯光束的传输问题[12]。

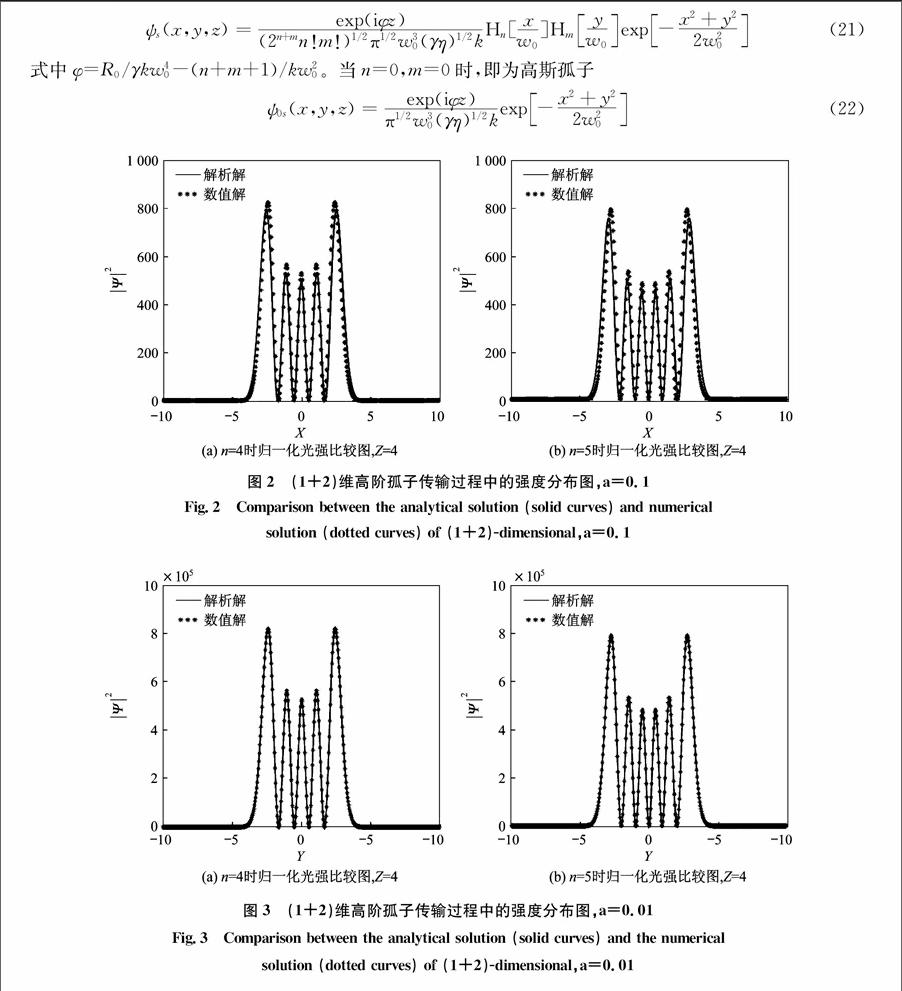
本文利用变分法解析出了（1+2）维非局域非线性薛定谔方程的解，并给出了数值模拟。讨论了厄米高斯光束在非局域非线性介质里面的传输特性，得到了厄米高斯光束解析解。数值模拟显示厄米高斯光束能够传输一段较长的距离而束宽保持不变，随着非局域程度的增大，解析解愈加接近数值解。

3 结 论

用解析的方法研究了非局域非线性介质中光束的传输特性，通过对非线性介质中响应函数的展开，使得非线性薛定谔方程得以简化，得到光束各参量在传输过程中的演化规律，求解出高阶高斯光束孤子解。通过解析解与数值模拟比较，发现随着非局域程度的增加，解析解更加接近数值解。

参考文献：

[1] SNYDER A W，MITCHELL D J.Accessible solitons[J].Science，1997，276（6）：1538-1541.

[2] CONTI C，PECCIANTI M，ASSANTO G.Route to nonlocality and observation of accessible solitons[J].Physical Review Letters，2003，91（7）：073901-1-4.

[3] CONTI C，PECCIANTI M，ASSANTO G.Observation of optical spatial solitons in a highly nonlocal medium[J].Physical Review Letters，2004，92（11）：113902-1-4.

[4] ROTSCHILD C，COHEN O，MANELA O，et al.Solitons in nonlinear media with an infinite range of nonlocality： First observation of coherent elliptic solitons and of vortex-ring solitons[J].Physical Review Letters2005，95（21）：213904-1-4.

[5] PECCIANTI M，CONTI C，ASSANTO G.All-optical switching and logic gating with spatial solitons in liquid crystals[J].Applied Physics Letters，2002，81（18）：3335-3337.

[6] PECCIANTI M，BRZDAKIEWICZ K A，ASSANTO G.Nonlocal spatial soliton interactions in nematic liquid crystals[J].Optics Letters，2002，27（16）：1460-1462.

[7] GUO Q，LUO B R，YI F H， et al.Large phase shift of nonlocal optical solitons[J].Physical Review，2004，69（1）：016602-1-8.

[8] HUANG Y，GUO Q，CAO J N.Optical beams in lossy nonlocal Kerr media[J].Optics Communications，2006，261（1）：175-180.

[9] HU W，ZHANG T，GUO Q，et al.Nonlocality-controlled interaction of spatial solitons in nematic liquid crystals[J].Applied Physics Letters，2006，89（7）：071111-1-3.

[10] BUCCOLIERO D，DESYATNIKOV A S，KROLIKOWSKI W，et al.Laguerre and Hermite soliton clusters in nonlocal nonlinear media[J].Physical Review Letters，2007，98（5）：053901-1-4.

[11] DENG D M，ZHAO X，GUO Q， et al.Hermite-Gaussian breathers and solitons in strongly nonlocal nonlinear media[J].Journal of the Optical Society of America B，2007，24（9）：2537-2544.

[12] BAI D F，HUANG C C，HE J F， et al.Variational solutions for Hermite-Gaussian solitons in nonlocal nonlinear media[J].Chinese Physics B，2009，18（7）：2853-2857.

[13] OUYANG S G，GUO Q，LAN S， et al.The solutions of the strongly nonlocal spatial solitons with several types of nonlocal response functions[J].Chinese Physics， 2007，16（8）：2325-2330.

[14] OUYANG S G，GUO Q，WU L， et al.Conservation laws of the generalized nonlocal nonlinear Schrodinger equation[J].Chinese Physics，2007，16（8）：2331-2337.

[15] BAI Z Y，DENG D M，GUO Q.Elegant Ince-Gaussian beams in a quadratic-index medium[J].Chinese Physics B，2011，20（9）：094202.

[16] BAI Z Y，DENG D M，GUO Q.Elegant Ince-Gaussian breathers in strongly nonlocal nonlinear media[J].Chinese Physics B，2012，21（6）：064218.

（编辑：程爱婕）