自然崩落法矿山井下大规模开采综合评价及模拟技术
刘洪均,彭平安,王李管
自然崩落法矿山井下大规模开采综合评价及模拟技术
刘洪均1,彭平安2,王李管2
(1. 北京科技大学 土木与环境工程学院,北,100083;2. 中南大学 资源与安全工程学院,湖南 长沙,410083)
为降低矿山采用自然崩落法存在的风险,为后续井下安全大规模开采提供保障,对自然崩落法矿岩可崩性和崩落后的块度分布规律进行综合评价及模拟,提出一种矿岩可崩性三维数字化评价方法和矿岩崩落块度预测算法。通过对评价区域的三维建模,基于地质统计学理论将矿岩岩体参数推估反演到离散化后的矿岩工程模型中,根据三维节理面Monte Carlo模拟原理对矿岩崩落块度进行三维重现。将上述方法用于云南省普朗铜矿进行验证。研究结果表明:普朗铜矿III级和IV级矿岩质量分数之和为99.1%,矿岩可崩性级别为III至IV,适合应用自然崩落法开采;原始崩落块度等效尺寸大于1.65m的块体筛上累积百分比为40%,建议普朗铜矿放矿口长×宽为5.00 m×5.00 m,此时放矿堵塞概率较小。
自然崩落法;可崩性评价;块度预测;地质统计学;Monte Carlo模拟
自然崩落法是一种开采成本低廉、劳动生产率高、科学指导下作业安全性好的采矿方法,被誉为地下采矿中的“露天开采”。自1895年问世以来,该方法已经在美国、智利、加拿大、南非、澳大利亚等矿业大国得到了广泛应用,并取得了良好效果[1]。我国从20世纪60年代开始,先后在云南省狮子山铜矿和湖北省金山店铁矿、程潮铁矿、丰山铜矿等矿山开展了自然崩落法的试验研究,并在山西省铜矿峪矿开启了我国矿山运用自然崩落法开采的先河[2−3]。自然崩落法是靠岩体内部的自然力使矿石破碎,并依靠自身重力进行矿石运搬的大规模地下采矿方法。自然崩落法的生产过程与传统采矿方法相比有很大不同,是一种优缺点非常明显的方法,其实施效果涉及矿岩的可崩性、崩落块度、崩落规律与崩落速度、放矿控制、崩落区崩落状态和非崩落区稳定性监测等多技术问题[4]。长期以来,国内外学者对自然崩落法相关理论方法进行了研究[5]。王少勇等[6]将模糊数学和物元分析结合研究了对矿岩可崩性进行评价的新方法;王家臣等[7]提出了单纯同调理论预测崩落块体大小的数学模型;姜增国等[8]则对矿石自然崩落规律进行了探讨。上述方法均立足于二维状态下以点带面的思想,即以某个小范围内的计算结果近似表征整个矿区结果。这种方法因没能考虑各参数的随机变化,其评价结论存在一定缺陷;另一方面,这些研究只针对自然崩落法技术研究中的某一个方面,未形成综合理论。为此,本文作者提出基于三维可视化的自然崩落法矿山井下大规模开采综合评价及模拟技术,并开发相应的三维评价系统,解决其中涉及的关键技术与实施方法,并以普朗铜矿为例,论述该方法的有效性和实用性。
1 技术原理与方法
自然崩落法矿山井下大规模开采综合评价及模拟技术以数据获取与分析、三维建模、可崩性评价、崩落矿岩块度预测为主线,综合运用数据库技术、GIS技术结合地质统计学、岩体等级(RMR)评价体系、Monte Carlo模拟等理论,其基本技术路线如图1所示。其中,数据获取与分析是一切工作的基础,而建立待评价区域的三维模型是本技术区别于传统方法的关键。矿岩的可崩性及崩落块度与岩体构造、矿岩强度、原岩应力状态有着密切的联系[9],因此,详尽的岩体构造调查、矿岩物理力学性质测定和地应力测定是综合评价结果的保障。而通过对待评价区域的三维建模,避免了传统方法以点带面方式存在的缺陷,能够更加准确、真实地反映研究对象。
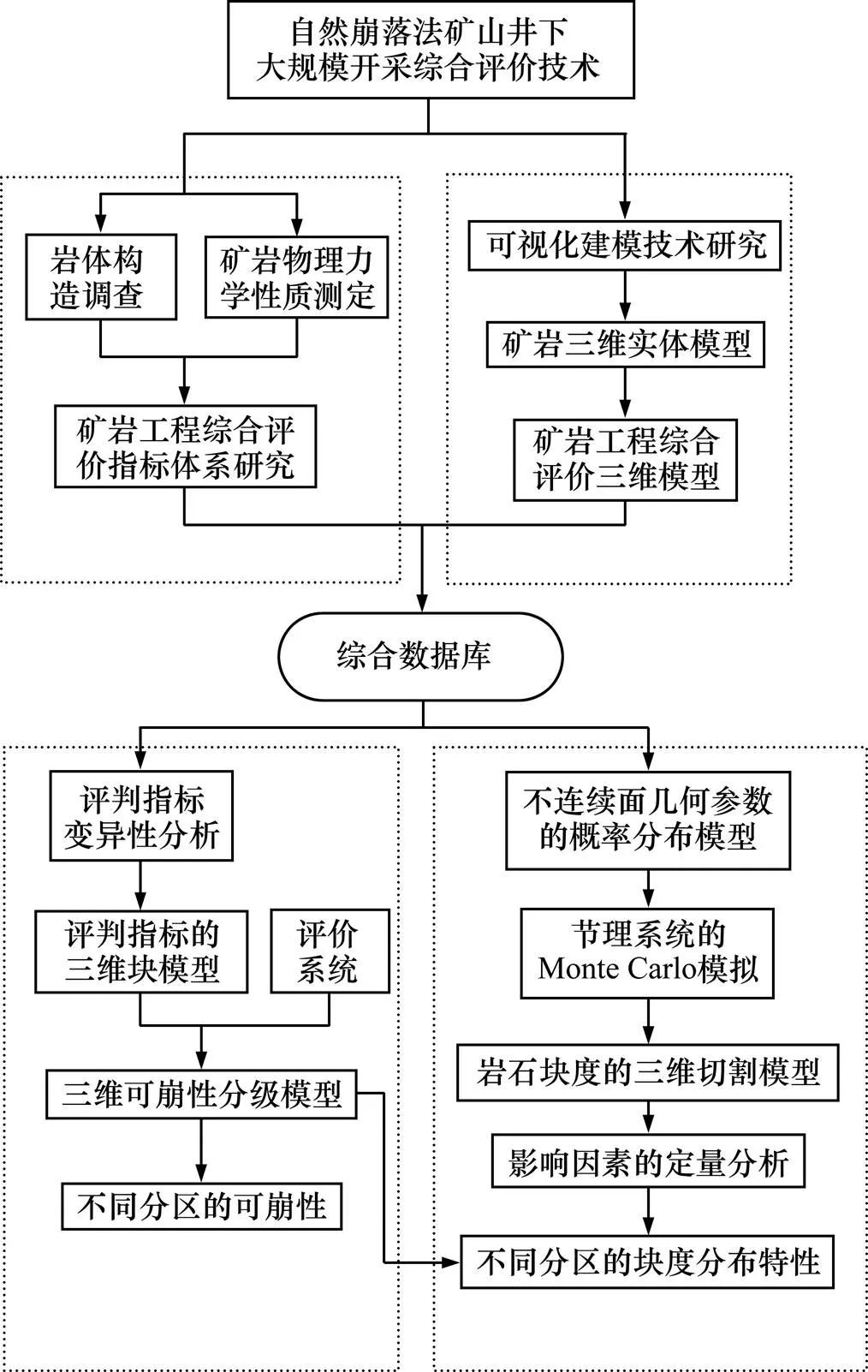
图1 自然崩落法矿山井下大规模开采综合评价及模拟技术路线
1.1 矿岩可崩性三维数字化评价方法
影响岩体质量的因素(如岩石强度、岩石质量指标QD、节理间距等)在空间内具有一定的随机性,同时又与周围一定范围内的变量有关,即表现出特定的分布规律。由于任何既具有随机性且具有结构性的呈现空间分布变量都称为区域化变量[10],因此,将这些因素视为区域化变量,以变异函数为工具对其空间结构性进行分析,根据区域化变量最优估值理论对各因素在岩体内的取值分别进行推估,最后综合各因素得到反映岩体工程质量的RMR模型。该方法的基本步骤如图2所示。

图2 矿岩可崩性三维数字化评价方法基本流程
基于修正的RMR评价体系,可对估值后的矿岩可崩性评价模型按级别、岩性、中段等类别进行多方位、多角度的深层次评价,应用Laubscher崩落图、Mathews稳定图[11]对各评价区域的水力半径进行预测。
1.2 基于三维节理表面模拟的矿岩块度预测算法
岩体可以视为被构造面切割而成的大小和形状各异的岩块集合体,同时岩体在破坏过程中将优先沿已有的裂隙面发生[12]。因此,可以岩体构造面的空间展布规律为基础,采用Monte Carlo模拟技术[13]、三维空间解析几何知识和三维实体切割技术,按照统计学原理模拟构造面的空间展布,并由此切割实体,统计实体内部由构造面切割出的岩块大小和形状分布组成,最后在块体形状分类的基础上统计得到崩落岩体的块度分布规律。该算法的流程如下。
1) 收集不连续面参数的统计数据,对构造空间分布规律进行分析,执行Monte Carlo模拟,产生不连续面综合数据库。
2) 研究沿测线方向计算从不连续面到坐标原点的垂直距离,形成三维节理面扫描文件。
3) 确定模拟位置及范围,生成模拟岩体的实体模型,用三维节理面切割实体模型。
4) 计算岩块的体积、面积及最大、中间和最小弦长,并判别岩块的形状特征。
5) 重复以上步骤,直至与模拟范围相交的节理面都参与了运算,输出结果。
6) 在指定方向上对经过上述计算的岩块进行切割,并计算二维特征参数。原始和崩落块度预测算法如图3所示,块体形状分布统计算法如图4所示。

图3 原始和崩落矿岩块度预测算法
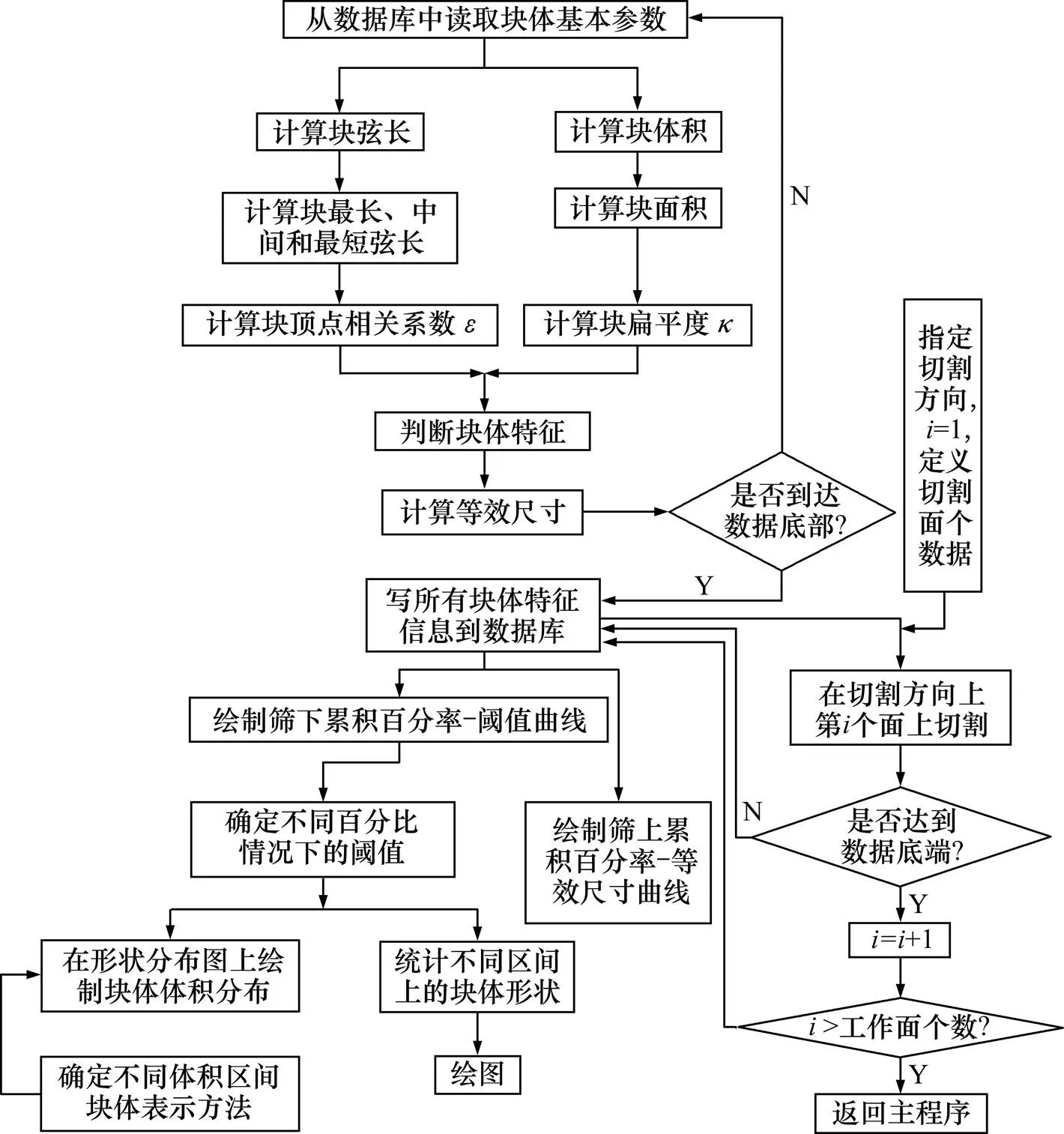
图4 块体形状分布统计算法
2 工程应用
普朗铜矿是2001年启动的大调查项目发现的特大型斑岩铜矿,截至2013年,普朗铜矿共探获铜资源储量480万t。一期采、选设计规模为年处理原矿石1 250万t,建成后将成为我国特大型地下开采金属矿山。考虑到普朗铜矿矿床厚大但品位低、岩层破碎和完整性差、工程地质条件恶劣及保护环境等综合情况,拟采用自然崩落法开采。
2.1 数据获取与分析
无论是进行矿岩可崩性评价还是崩落块度的预测,大量详实的岩体工程观测资料和测试数据是保证工作的前提。岩体结构调查一般采用钻孔岩芯和坑道暴露面联合调查的方式进行。通过对获得的资料进行统计分析,获得有关岩石强度、岩石质量指标、结构面产状、间距等统计特征与统计参数,因此,就不难应用计算机推估未知区域的岩体和结构面特征以及再现符合这种统计特征的岩体和结构面网络,从而在计算机上研究矿岩的可崩性和崩落块度。
普朗铜矿先后开展了大规模的岩体构造调查工作,2006年施工钻孔29孔,钻孔施工长度9 985.82 m;2012年施工钻孔11孔,钻孔施工长度3 369.75 m,同时在3900中段和3720中段进行暴露面岩体原位调查工作,调查坑道总长度为1 152.82 m。获得的主要数据包括结构面产状(含倾角、倾向、结构面分组等)、结构面间距、粗糙度、张开度、持续性、QD以及由点载荷试验得到的岩石单轴抗压强度、水文地质条件等。
根据调查得到的节理产状,作Schmidt极点等密图,如图5所示。从图5可以看出:普朗铜矿可分为3组优势节理组,其倾向范围分别为125°~195°,196°~240°和320°~359°。经统计,各组节理的倾向与倾角均服从正态分布。

图5 普朗铜矿节理产状极点等密图
获得节理间距有效数据21 073条,统计得节理间距均值为0.27 m,直方图如图6(a)所示。从图6(a)可见:经P−P图验证,正态分布P−P图拟合误差较大,趋势偏差达到0.20左右;指数分布P−P图拟合较好,趋势偏差为0.05左右;经自然对数转换后的正态分布拟合性最好,趋势偏差为0.02左右。因此,可以认为普朗铜矿结构面间距服从对数正态分布,如图6(b)所示。
此外,对结构面粗糙度、张开度、节理持续性、RQD值、岩芯单轴抗压强度等都进行了统计分析。
2.2 三维可视化建模
地质建模是对实际矿体的一种近似模拟,借助于先进的理论和技术,充分利用有限的地质资料,建立合理、可靠的地质模型是自然崩落法研究中的关键。地质体模型建立以后,要准确、完整地表达地质体的空间形态和内部属性,就需要对模型进行离散化。常用的离散化方法是采用矢量模型与栅格模型相结合的方式,即建立块段模型。块段模型的基本思想是将矿床在三维空间内按照一定的尺寸划分为众多的单元块,然后对填满整个范围内的单元块的信息根据已知信息进行推估,并在此基础上进行计算。
根据地质原始资料构建的普朗铜矿地质体模型及块段模型如图7所示。块段模型坐标尺寸如表1所示。
宋榕华:在产业链上的合作伙伴受到环保政策影响加大的形势下,公司近两年加大了推广社会责任的力度。不只把自己的企业管理好,而且兼顾上游下游的企业,让整个产品的生命周期都得到管理。比如公司的诸多供应商中,尤其是一些本地的私营企业,在环保检查方面不够成熟,公司就帮助他们进行环保合规性检查。为他们做出一个详细的检查表,内容包括内部管理情况、环保政策落实情况、产品是否环保等诸多方面。让他们根据表格内容先期按照国家相关规定进行自查,由此查漏补缺,不断合规起来。这样一来企业不用担心政府检查,科莱恩与他们合作也觉得放心。

(a) 地表DTM模型;(b) 矿体模型;(c) 岩体模型;(d) 约束后的块段模型

表1 普朗铜矿块段模型基本参数
2.3 可崩性评价
为更适应自然崩落法的研究要求,对RMR评价标准进行适当修正,以岩石单轴抗压强度(c)、岩石质量指标(QD)、节理间距(J)、节理条件(c)和地下水条件(w)作为评价岩体质量基本指标[14],然后对各分类指标按区间进行评分,最后相加即得岩体质量评价的基本RMR值(RMR)。由于节理条件和地下水条件乃定性因素,为利用调查数据对评价模型中的相应因素打分进行估值,必须对其进行量化。其中地下水条件根据钻孔水文调查结果,对整个矿区打分。节理条件的量化根据王文星等[15]对节理表面形貌与结构面剪切强度关系之间的研究,提出用结构面摩擦角量化结构面粗糙度的方法,其关系式为
式中:为结构面摩擦角(°);为粗糙度指标,对于粗糙型、平坦型和光滑型3类粗糙度,其对应的分别为18.2°,16.5°和11.4°。
将岩石单轴抗压强度(c)、岩石质量指标(QD)、节理间距(s)和摩擦角(J)视为区域化变量,利用变异函数对其进行空间结构性与变异性分析。图8所示为摩擦角在矿体走向、倾向和厚度方向上的试验和理论变异函数(图中为滞后距,()为变异函数),由此得各参数的变程、块金及基台值如表2所示。最后利用克里格方法对各评价参数进行空间插值,得到矿区整体矿岩可崩性三维RMR评价模型,如图9所示。

(a) 走向方向;(b) 倾向方向;(c) 厚度方向

表2 理论变异函数参数表
注:0为块金常数;为拱高;0+为基台值;为变程。
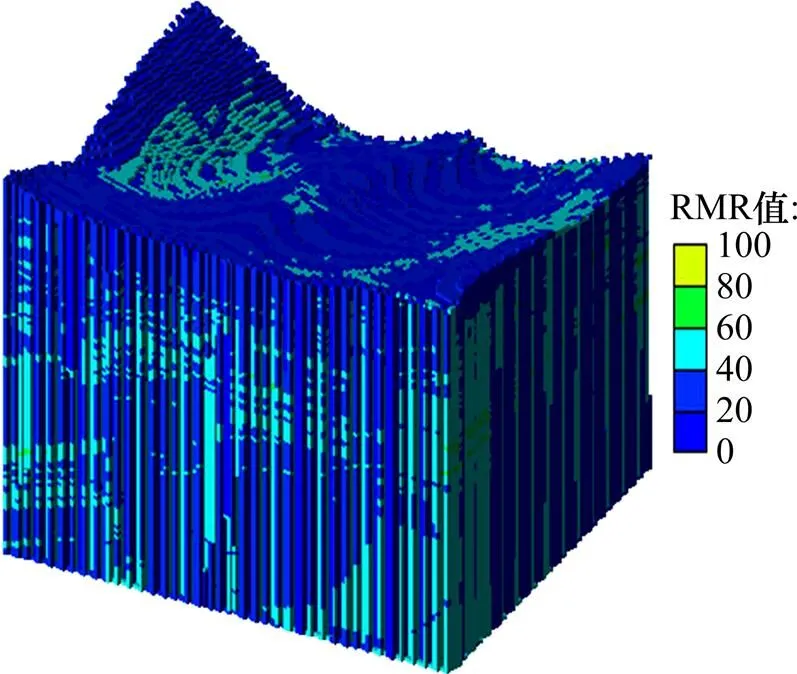
图9 普朗铜矿矿岩可崩性RMR评价模型
根据劳布施尔(Laubscher)的评价标准[16],分析不同可崩性级别内的矿岩所占比例,结果如表3所示。从表3可以看出:该矿矿岩可崩性主要分为II级、III级、IV级和V级,其中III和IV级占总体积的99.1%,整体矿岩可崩性为较好—好,适合使用自然崩落法进行大规模开采。在该模型基础上也可快速对矿区不同级别、不同岩性、不同中段的矿岩RMR值(RMR)进行统计,对其可崩性进行评价。

表3 普朗铜矿矿岩可崩性评价结果
根据矿岩可崩性评价结果,基于Laubscher 崩落图和Mathews稳定图对普朗铜矿持续崩落水力半径进行预测,结果如表4所示。从表4可以看出:持续崩落水力半径都较小,从另一方面说明在普朗铜矿应用自然崩落法开采是可行的。
表4 普朗铜矿持续崩落水力半径
Table 4 Chart of caving hydraulic radius of Pulang Copper Mine m

序号对象Laubscher 崩落图法Mathews稳定图法 1上盘岩体22.626.2 2矿体21.625.6 3下盘岩体22.327.5
2.4 矿岩崩落块度预测
根据所提算法,以普朗铜矿综合数据库中数据为输入参数,对普朗铜矿矿岩崩落块度进行预测。其中矿岩的节理产状见图5,节理间距参数见图6。节理迹长为2.5 m,模拟岩块范围(长×宽×高)为10 m×10 m×10 m,不连续相关因子为0.5。
切割完成后产生的模拟块体形状如图10所示。图10中,等于块体上较长弦所定义向量之间的平均夹角的余弦乘以10,用于描述物体的细长性;用于表述物体的容积系数;25,50和75分别表示占总体积25%,50%和75%时的块体体积。对产生的切割块体结果进行统计,得到的矿岩块度体积区间分布如图11(a)所示,其中C代表立方体,CE代表立方−细长体,PC代表扁平−立方体,P代表扁平体,EP代表细长−扁平体,E代表细长体。块体体积筛下累积百分率如图11(b)所示,矿岩块度的筛上累积比例如图11(c)所示。

(a) 块体切割结果;(b) 不同块体体积的形状分布
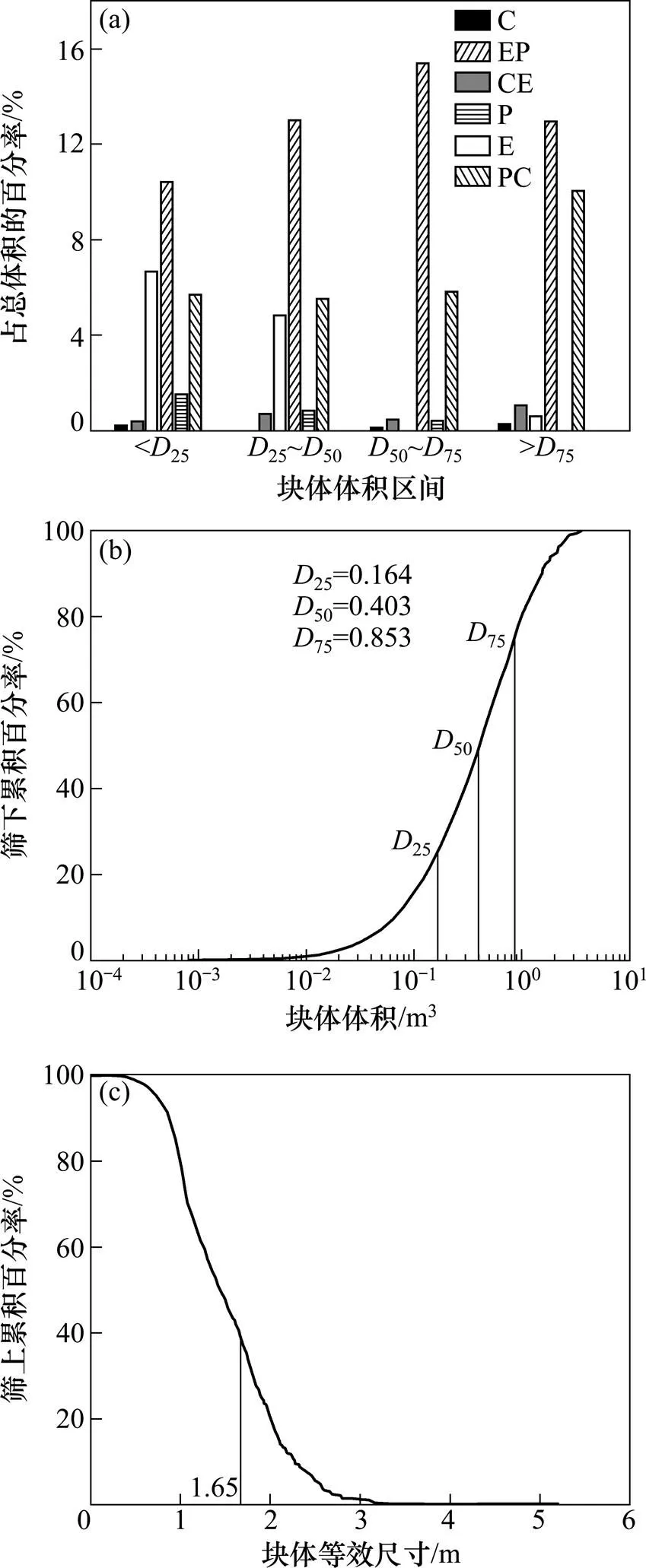
(a) 不同体积区间上各形状块体占总体积百分率; (b) 块体体积筛下累积百分率;(c) 矿岩块度筛上累积百分率
图11 矿岩崩落块度分布曲线
Fig. 11 Block caving distribution curve
从图11(b)可以看出:块体筛下体积的四分位点分别为0.164,0.403和0.853 m3。从图11(c)可以看出:当等效尺寸大于0.50 m而小于3.00 m时,等效尺寸曲线下降比较快,这说明块体等效尺寸落在这个区间体积比例较大;等效尺寸大于1.65 m的块体筛上累积体积比例为40%,大于1.26 m的块体筛上累积体积比例为59.85%。大量大块率对放矿影响的实验结果表明:当大块(即块度尺寸大于1/3放矿口宽度)超过40%时,卡斗现象频繁发生。因此,建议普朗铜矿放矿口的长×宽为5.00 m×5.00 m,此时放矿时堵塞的概率较小。
3 结论
1) 将影响矿岩可崩性的各参数视为区域化变量,基于地质统计学理论提出了一种矿岩可崩性三维数字化评价新方法,为全面准确地研究自然崩落法开采可行性提供了新途径。
2) 应用本文所提方法,建立了反映普朗铜矿矿岩可崩性的三维RMR模型,得普朗铜矿总体矿岩质量可分为II级、III级、IV级和V级,其中III和IV级占总体积比例为99.1%,矿岩可崩性级别为III至IV,说明在普朗铜矿应用自然崩落法进行大规模开采是可行的。
3) 基于Monte Carlo模拟、空间解析几何理论和三维实体切割技术提出了矿岩块度预测算法,对普朗铜矿矿岩崩落块度进行预测,得原始崩落块度等效尺寸大于1.65 m的块体筛上累积体积比例为40%。建议普朗铜矿放矿口的长×宽为5.00 m×5.00 m,此时放矿时堵塞的概率较小,所得成果为后续采矿方法设计及工程中的放矿控制提供了重要依据。
[1] Brown E T. Block caving geomechanics[M]. 2nd ed. Queensland: The University of Queensland, 2007: 19−28.
[2] 刘育明. 自然崩落法的发展趋势及在铜矿峪矿二期工程中的技术创新[J]. 采矿技术, 2012, 12(3): 1−4.
LIU Yuming. Development tendency of block caving method and technological innovation in the second phase of Tongkuangyu mine[J]. Mining Technology, 2012, 12(3): 1−4.
[3] 袁海平, 曹平. 我国自然崩落法发展现状与应用展望[J]. 金属矿山, 2004, 338(8): 25−28.
YUAN Haiping, CAO Ping. Present status of block caving development and its application prospect in China[J]. Metal Mine, 2004, 338(8): 25−28.
[4] Brady B H G, Brown E T. Rock mechanics: For underground mining[M]. Berlin: Springer, 2007: 126−134.
[5] Rogers S, Elmo D, Webb G, et al. Volumetric fracture intensity measurement for improved rock mass characterisation and fragmentation assessment in block caving operations[J]. Rock Mechanics and Rock Engineering, 2013, 56(4): 1−17.
[6] 王少勇, 吴爱祥, 韩斌, 等. 自然崩落法矿岩可崩性模糊物元评价方法[J]. 岩石力学与工程学报, 2014, 33(6): 1241−1247.
WANG Shaoyong, WU Aixiang, HAN Bin, et al. Fuzzy matter-element evaluation of ore-rock cavability in block caving method[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1241−1247.
[7] 王家臣, 熊道慧, 方君实. 矿石自然崩落块度的拓扑研究[J]. 岩石力学与工程学报, 2001, 20(4): 443−447.
WANG Jiachen, XIONG Daojun, FANG Junshi. Topological study on natural caving blocks of ore body[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 443−447.
[8] 姜增国, 杨保仓. 基于DDEM的自然崩落采矿法崩落规律的数值模拟[J]. 岩土力学, 2005, 26(2): 239−242.
JIANG Zengguo, YANG Baocang. Numerical simulation of caving law in natural caving mining method based on deformable discrete element method[J]. Rock and Soil Mechanics, 2005, 26(2): 239−242.
[9] William A H, Richard L B. Underground mining methods: Engineering fundamentals and international case studies[M]. Colorado: SME, 2001: 85−93.
[10] 贾明涛, 王李管. 基于区域化变量及RMR评价体系的金川Ⅲ矿区矿岩可崩性评价[J]. 岩土力学, 2010, 31(6): 1907−1912.
JIA Mingtao, WANG Liguan. Evaluation of rockmass quality based on regionalization variable optimal estimation theory and RMR system in Jinchuan mine No.3[J]. Rock and Soil Mechanics, 2010, 31(6): 1907−1912.
[11] 何昌盛. 基于岩体结构特征分析的可崩性分级研究[J]. 采矿与安全工程学报, 2012, 29(6): 845−851.
HE Changsheng. Study on cavability classification based on analysis of rock mass structure characteristics[J]. Journal of Mining & Safety Engineering, 2012, 29(6): 845−851.
[12] Xu C, Dowd P A, Wyborn D. Optimisation of a stochastic rock fracture model using Markov chain Monte Carlo simulation[J]. Mining Technology, 2013, 122(3): 153−158.
[13] Ball G H, Clark J B, Gifford M, et al. Block size distribution analysis of a fractured rock mass-case study:OZ Minerals’ Carrapateena project[J]. Mining Education Australia, 2014, 29(2): 13−19.
[14] 冯兴隆, 王李管, 毕林, 等. 基于三维模拟技术的矿岩可崩性评价[J]. 煤炭学报, 2008, 33(9): 971−976.
FENG Xinglong, WANG Liguan, BI Lin, et al. Cavability of rock mass based on 3D simulation technology[J]. Journal of China Coal Society, 2008, 33(9): 971−976.
[15] 王文星, 潘长良. 矿体可崩性研究及其在自然崩落法采矿中的应用[J]. 矿冶工程, 1996, 16(3): 16−18+21.
WANG Wenxing, PAN Changliang. The investigation of orebody cavability and its use in the design of natural caving methods[J]. Mining and Metallurgical Engineering, 1996, 16(3): 16−18+21.
[16] 江飞飞, 李向东, 张华军, 等. 急倾斜厚大矿体自然崩落块度预测及分布规律研究[J]. 矿业研究与开发, 2014, 34(2): 6−9.
JIANG Feifei, LI Xiangdong, ZHANG Huajun, et al. Research on block caving fragmentation prediction and its application of thick orebody with steep dip angle[J]. Mining Research and Development, 2014, 34(2): 6−9.
Comprehensive evaluation and simulation for large-scale mining using natural caving method
LIU Hongjun1, PENG Pingan2, WANG Liguan2
(1. School of Civil and Environmental Engineering,University of Science and Technology Beijing, Beijing 100083, China;2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
To reduce the risk of mining by natural caving method and to guarantee the safety of subsequent large-scale underground mining, the ore rock cavability and the fragmentation distribution were evaluated. Additionally, a three-dimensional digital evaluation method of ore rock cavability as well as an algorithm of was proposed. Through 3D modeling of evaluation regional, a discretized mineral engineering model was inversed with the parameters collocation of rock body based on geostatistics. Finally, the 3D caved block was rebuilt using Monte Carlo simulation. The above method was applied to Pulang Copper Mine, Yunnan Province. The results show that the mass fraction of level III and IV rock is 99.1%, and the rock cavability level is III to IV, it is suitable for natural caving mining. The percentage of original block equivalent size larger than 1.65 m is 40%. So the mouth size of Pulang Copper Mine is recommended 5 m×5 m, and in which situation the possibility of ore blocking is less.
natural caving method; cavability evaluation; fragmentation prediction; geostatistics; Monte Carlo simulation
TD 853.36
A
1672−7207(2015)02−0617−08
2014−08−07;
2014−10−12
国家高技术研究发展计划(863计划)项目(2011AA060407)(Project (2011AA060407) supported by the National High Technology Research and Development Program of China(863 Program))
彭平安,博士研究生,从事数字矿山方向研究;E-mail:ping_an@outlook.com
10.11817/j.issn.1672-7207.2015.02.033
(编辑 陈灿华)

