应力敏感油藏多角度裂缝压裂水平井产量模型

方思冬，程林松，李彩云，曹仁义，杨 戬，何聪鸽

（1.中国石油大学（北京）石油工程学院，北京 102249； 2.中国石油长庆油田公司 勘探开发研究院，陕西 西安710000； 3.中国石油勘探开发研究院，北京 100083）

0 引言

低渗透致密储层油气资源量巨大，但普遍具有低孔隙度低渗透率和较强应力敏感等特点，开发难度大［1］.对此，压裂水平井是关键的开采技术.多年来，已有众多学者对低渗透和致密油气藏应力敏感进行实验和理论研究，得到描述储层应力敏感方法和回归重要参数，对高效合理开发低渗透油藏提供了基础［2-6］.薛永超等［5］通过大量低渗透实际岩心实验得到不同渗透率级别下应力敏感因数，而文献［7］的因数回归方法被普遍采用.同时，人们基于势理论对压裂水平井稳定产量［8-11］及基于格林函数和拉斯变换对不稳定渗流［12-19］进行大量研究，并形成系统的理论和方法，但以上稳定和不稳定方法都是以线性渗流为前提.然而，实际地层由于复杂的地应力变化，人工裂缝通常与井筒呈一定角度，目前将应力敏感表征和多角度缝压裂水平井结合起来研究的很少.因此，笔者基于摄动理论［20-21］，考虑应力敏感表征，结合拉普拉斯变换，建立并求解考虑储层应力敏感的多段多角度裂缝压裂水平井不稳定渗流数学模型，分析流动形态，明确储层应力敏感性对产量的影响，得到不同裂缝参数下的产量特征，其结果对于低渗透致密储层压裂水平井产量评价和参数优化具有指导意义.

1 水平井数学模型

1.1 物理模型

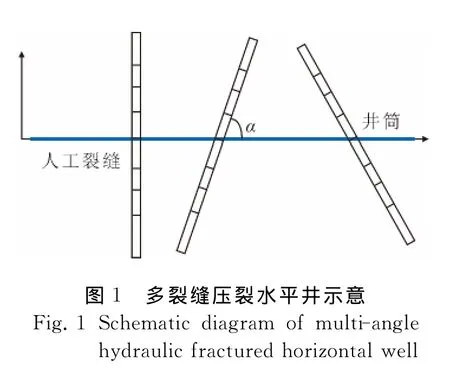
水平井穿过多条与水平井筒存在一定夹角α的裂缝见图1.整个油藏为水平等厚、均质油藏；油藏顶底封闭，只考虑无限大外边界；水平井仅在裂缝处射孔生产；水平井定产生产，不考虑井筒摩阻引起的附加压力降，各条裂缝在井筒处压力相等；水平井井筒和人工裂缝均为无限导流；地层和流体均微可压缩，流体为单相，且地层中流动符合达西定理.

1.2 裂缝流动模型

1.2.1 地层渗流

地层渗透率应力敏感数学模型［21］为

式中：K为地层瞬时渗透率；Ki为地层原始渗透率；γ为应力敏感因数；pi为原始地层压力；p为地层压力.

引入量纲为一的数将单相不稳定渗流方程化为

1.2.2 摄动线性化

式（2）非线性较强，不能直接求出解析解，因此引入摄动变换，即

将式（2）转化为

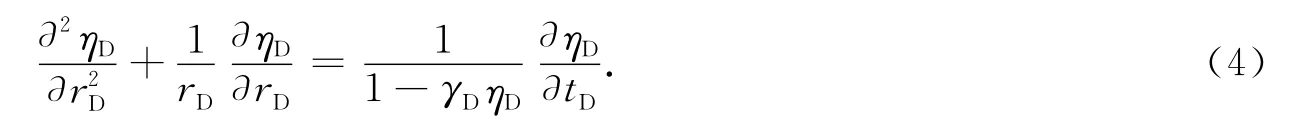
由于γD在实际油藏中通常为一小量，可以将η按照γD展开为级数形式，即

对于低渗透储层，γD很少超过0.2，二阶项的数量级远远小于1阶解［22］，因此，将式（4）的零阶解与一阶解同时进行拉普拉斯变换作为下一步求解裂缝流动的基函数，即

式（7-8）中：K0为零阶贝塞尔函数；E1为冥积分函数；s为拉氏空间变量.

式（8）中积分项用四节点高斯—拉盖尔数值积分［23］表示为

1.2.3 人工裂缝

将每条裂缝离散成一维单元见图1.整个渗流方程是非线性的，无法直接利用叠加原理，但叠加原理可以用于摄动解，零阶和一阶摄动解均是线性解.基于此，分别在零阶和一阶摄动空间下线积分得到裂缝单元线源函数表达式为

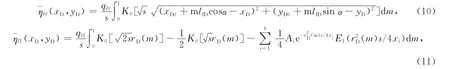
1.3 模型求解

假设压裂的裂缝条数为n，每条裂缝离散单元个数为m（i），i＝1～n，每一条压裂裂缝都可以在井筒的任意位置.认为压裂裂缝都在相同的井筒压力下生产，即为水平井无限导流能力模型.裂缝为无限导流能力，即同一条裂缝不同单元压力相同水平井总的流量是每条压裂裂缝中流出流量的总和.

零阶摄动空间下流量ql0i和压力ηD0ij满足表达式为

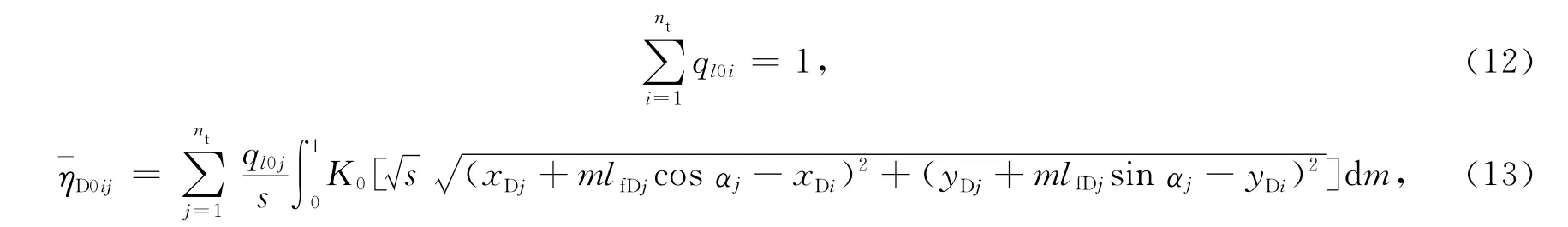
式（12-13）中：nt为裂缝分段数；j＝1／nt.

将每个单元对应式（12）、（13）相应的公式形式写成矩阵方程组为

在Laplace空间下分别计算得到井底压力零阶和一阶摄动解，再利用Stehfest数值反演方法［24］求得实空间下井底压力零阶和一阶摄动解，并变换得到井底压力pD为

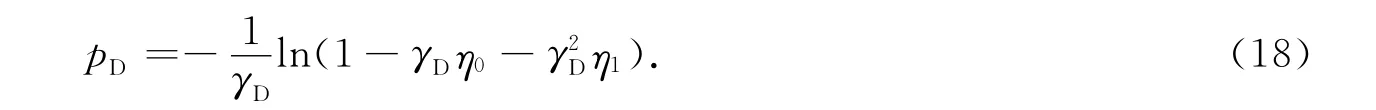
利用拉普拉斯空间下无因次压力和无因次产量的关系［25］，由定产生产井底压力解求出定压生产的产量qD，即

式中：qD为无因次产量

2 模型验证

以无因次应力敏感因数γD为0.1，3条无限导流裂缝压裂水平井为例，定产油量分析井底压力，将模型计算结果与数值模拟软件Eclipse考虑应力敏感的裂缝LGR加密计算结果进行对比.该压裂水平井模型数值模拟压力分布见图2（a），对比图2（b）中模型无因次井底压降和数值模拟无因次井底压降，2条无因次曲线基本重合.

3 流动形态

压裂水平井流动形态与流动阶段受水平井长度（水平井只在裂缝处射孔）和裂缝条数影响很小，见图3（a）.因此，假设油藏为各向同性，选取存在3条与井筒呈不同角度的压裂裂缝，裂缝两翼不等长.无因次参考长度选取最长裂缝半长.各参数取值：裂缝1半长依次为100m；夹角依次为0.33π（60°）；裂缝2半长依次为120m；夹角为0.5π（90°）；裂缝3半长依次为80m，夹角依次为0.38π（70°）；裂缝间距为80m.裂缝为无限导流.无因次化后计算考虑应力敏感和不考虑应力敏感无因次井底压降见图3（b）.根据压力和压力导数曲线分析，流动形态分3种：（1）地层线性流动阶段，指在流动初期地层中流体线性的流向各条压裂裂缝，无因次压降分布见图4（a）.在双对数图上表现为无因次压力导数曲线为1／2斜率的直线段.（2）过渡流阶段，该阶段没有明显特征.（3）拟径向流动阶段，是指对于整个油藏，如果生产时间很长，且压力波未传播到边界，则流体以拟径向流的形式向水平井及压裂裂缝区域流动，无因次压降分布见图4（b）.对于无应力敏感油藏，该流动段在双对数诊断图上表现为无因次压力导数曲线为0.5水平直线段；而存在应力敏感油藏，其径向流阶段，压力导数曲线上翘，主要因为地层压力下降，近井裂缝区渗透率下降很大，造成流动阻力增大.

4 产量分析

4.1 应力敏感

与前面假设相似，以3条无限导流裂缝压裂水平井为例，计算不同无因次应力敏感因数下产量qD变化见图5.由图5可知，压裂水平井流动初期为地层向裂缝的线性流动，压降幅度小，应力敏感对产量影响较小，图中初期5条曲线几乎重合.但当拟径向流动阶段，随着压降范围和幅度的增大，应力敏感因数对产量影响变大，并且产量变化幅度随着应力敏感因数增大而增大.

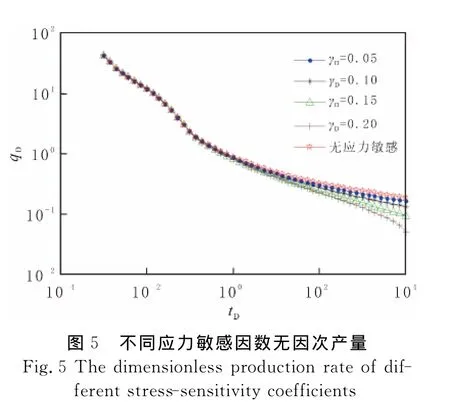
4.2 裂缝条数

根据以往文献资料［9，10，15］和本文模型特点分析在应力敏感条件下裂缝条数和裂缝角度对产量的影响.而针对常规裂缝参数对压力动态和产量的影响在以往的文献中有详细的分析［24，26］.

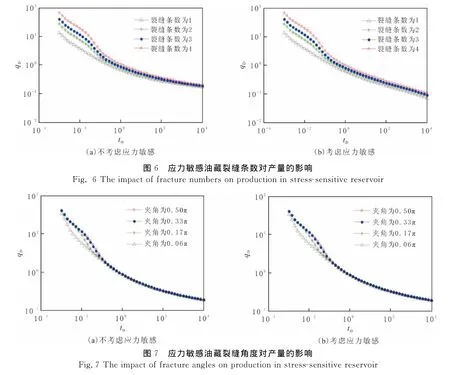
随着压裂工艺技术的不断完善和提高，多裂缝压裂得到广泛应用.提高裂缝条数是增加产量的重要手段，然而裂缝条数越多，产量增加幅度越小，在一定经济条件下过多的压裂是不合理的.应力敏感油藏裂缝条数对产量的影响见图6，图6（a）没有考虑应力敏感，图6（b）考虑应力敏感（无因次应力敏感因数为0.15），裂缝条数对初期产量影响较大，后期影响程度减小，然而考虑应力敏感的曲线后期产量差距明显，应力敏感减弱了裂缝间干扰作用.因此，实际油藏存在应力敏感的情况下，压裂裂缝数目应比不考虑应力敏感优化的裂缝条数多才能达到同样的增产效果.

4.3 裂缝与井筒角度

目前对裂缝与井筒角度对压力和产量的影响研究较少.假设水平井压裂3条裂缝，裂缝半长为100 m，裂缝间距为50m，裂缝为无限导流能力，通过分析不同裂缝与井筒角度井底压力（见图7），裂缝与井筒角度越大，无因次产量越大，当裂缝与井筒垂直时，产量达到最大值.对比图7（a）不考虑应力敏感和图7（b）考虑应力敏感（无因次应力敏感因数为0.1）曲线特征知，两者曲线形态几乎相同，都是角度对初期产量影响大，后期影响弱，因为应力敏感对产量后期影响大，而线性流动阶段影响较小；当裂缝与井筒角度小于0.33π，角度越小，产量减少越多.

5 结论

（1）基于摄动方法，推导拉普拉斯空间下零阶和一阶裂缝线源解，分别利用叠加原理，求解多角度多裂缝在零阶和一阶摄动空间的井底压力，并利用变换式得到实空间下考虑应力敏感非线性渗流压裂水平井产量.

（2）应力敏感油藏压裂水平井流动形态在压力导数的双对数曲线也呈现较明显的裂缝线性流与系统径向流动形态，然而应力敏感模型所得的双对数压力及其导数曲线在系统径向流阶段出现上翘，且无量纲渗透率模量数值越大，曲线上翘越明显，说明压差增加，应力敏感对产量影响越大.

（3）应力敏感因数越大，流动后期产量越小；而应力敏感效应减弱了缝间干扰作用，不同裂缝条数考虑应力敏感的曲线后期产量差距比不考虑应力敏感明显，因此，实际油藏存在应力敏感的情况下，压裂裂缝数目应比不考虑应力敏感优化的裂缝条数多才能达到同样的增产效果；裂缝与井筒夹角越大，无因次产量越大，当裂缝与井筒垂直时，产量达到最大值.

（References）：

［1］黄延章.低渗透油层渗流机理［M］.北京：石油工业出版社，1998：58-79.Huang Yanzhang.The mechanism of flow in low permeability reservoir［M］.Beijing：Petroleum Industry Press，1998：58-79.

［2］李传亮.应力敏感对油井产量的影响［J］.西南石油大学学报：自然科学版，2009，31（1）：170-172.Li Chuanliang.Stress sensitivity influence on oil well productivity［J］.Journal of Southwest Petroleum University：Science ＆ Technology Edition，2009，31（1）：170-172.

［3］高建，吕静，王家禄.储层条件下低渗透岩石应力敏感评价［J］.岩石力学与工程学报，2009（S2）：3899-3902.Gao Jian，Lv Jing，Wang Jialu.Evaluation on stress sensitivity of low permeability rock under reservoir condition［J］.Chinese Journal of Rock Mechanics and Engineering，2009（S2）：3899-3902.

［4］代平.低渗透应力敏感油藏实验及数值模拟研究［D］.成都：西南石油大学，2006.Dai Ping.The experiment and reservoir simulation of low permeability stress sensitive reservoirs［D］.Chengdu：Southwest Petroleum University，2006.

［5］薛永超，程林松.不同级别渗透率岩心应力敏感实验对比研究［J］.石油钻采工艺，2011，33（3）：38-41.Xue Yongchao，Cheng Linsong.Experimental comparison study on stress sensitivity of different permeability cores［J］.Oil Drilling ＆Production Technology，2011，33（3）：38-41.

［6］孙贺东，韩永新，肖香姣，等.裂缝性应力敏感气藏的数值试井分析［J］.石油学报，2008，29（2）：270-273.Sun Hedong，Han Yongxin，Xiao xiangjiao.Numerical well test analysis of stress-sensitive fractured gas reservoir［J］.Acta Petrolei Sinica，2008，29（2）：270-273.

［7］王培玺，刘仁静.低渗透储层应力敏感因数统一模型［J］.油气地质与采收率，2012，19（2）：75-77.Wang Peixi，Lu Renjing.Universal model of stress sensitive coefficient for low permeability reservoir［J］.Petroleum Geology and Recovery Efficiency，2012，19（2）：75-77.

［8］张德良，张烈辉，赵玉龙.低渗透气藏多级压裂水平井稳态产量模型［J］.油气地质与采收率，2013，20（3）：107-110.Zhang Deliang，Zhang Liehui，Zhao Yulong.Study on steady productivity of fractured horizontal well in low permeability gas reservoir［J］.Petroleum Geology and Recovery Efficiency，2013，20（3）：107-110.

［9］牟珍宝，袁向春，朱筱敏.低渗透油藏压裂水平井产量计算方法［J］.现代地质，2009，23（2）：37-40.Mu Zhenbao，Yuan Xiangchun，Zhu Xiaomin.The calculating method of horizontal wells with hydraulic fractures for low permeability reservoirs［J］.Geoscience，2009，23（2）：37-40.

［10］范子菲，方宏长，牛新年.裂缝性油藏水平井稳态解产量公式研究［J］.石油勘探与开发，1996，15（3）：52-57.Fan Zifei，Fang Hongchang，Niu Xinnian.A steady solution formula of horizontal well productivity in a fractured reservoir［J］.Petroleum Exploration and Development，1996，15（3）：52-57.

［11］王志平，朱维耀，岳明，等.低、特低渗透油藏压裂水平井产量计算方法［J］.北京科技大学学报，2012，34（7）：750-754.Wang Zhiping，Zhu Weiyao，Yue Ming，et al.A method to predict the production of fractured horizontal wells in low／ultralow permeability reservoirs［J］.Journal of University of Science and Technology Beijing，2012，34（7）：750-754.

［12］Gringarten A C，Ramey H J.Unsteady-state pressure distributions created by a well with a single horizontal fracture，partial penetration，or restricted entry［R］.SPE 3819，1974.

［13］Guo G，Evans R D.Pressure-transient behavior and inflow performance of horizontal wells intersecting discrete fractures［R］.SPE 26446，1993.

［14］Valko P，Amini S.The method of distributed volumetric sources for calculating the transient and pseudosteady-state productivity of complex well-fracture configurations［R］.SPE 106279，2007.

［15］Zhu D，Magalhaes F，Valko P.Predicting the productivity of multiple-fractured horizontal gas wells［R］.SPE 106280，2007.

［16］Ozkan E，Raghavan R.Some new solutions to solve problems in well test analysis：part 1-analytical considerations［R］.SPE，1998.

［17］Raghavan R S，Chen C C，Agarwal B.An analysis of horizontal wells intercepted by multiple fractures［R］.SPE 27652，1997.

［18］Brown M，Ozkan E，Raghavan R，et al.Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs［R］.SPE 125043，2010.

［19］Ozkan E，Brown M L，Raghavan R.Comparison of fractured-horizontal-well performance in tight sand and shale reservoirs［R］.SPE 121290，2010.

［20］Pedrosa O A.Pressure transient response in stress-sensitive formations［R］.SPE 15115，1986.

［21］同登科，陈钦雷，廖新维.非线性渗流力学［M］.北京：石油工业出版社，2003：97-104.Tong Dengke，Chen Qinlei，Liao Xinwei.Nonlinear flow dynamics in porous media［M］.Beijing：Petroleum Industry Press，2003：97-104.

［22］刘春凤，何亚丽.应用数值分析［M］.北京：冶金工业出版社，2005：155.Liu Chunfeng，He Yali.Applied numerical analysis［M］.Beijing：Metallurgical Industry Press，2005：155.

［23］同登科，陈钦雷.关于Laplace数值反演stehfest方法的一点注记［J］.石油学报，2001，11（6）：91-92.Tong Dengke，Chen Qinlei.A note on stehsfest numerical inversion of Laplace transforms［J］.Acta Petrolei Sinica，2001，11（6）：91-92.

［24］Van Everdingen，Hurst H W.The application of the Laplace transformation to flow problems in reservoirs［R］.SPE 949305，1949.

［25］尹洪军，杨春城，徐子怡，等.分段压裂水平井压力动态分析［J］.东北石油大学学报，2014，34（3）：75-80.Yin Hongjun，Yang Chuncheng，Xu Ziyi，et al.Pressure analysis of multi-fractured horizontal well［J］.Journal of Northeast Petroleum University，2014，34（3）：75-80.

［26］任俊杰，郭平，王德龙，等.页岩气藏压裂水平井产量模型及影响因素［J］.东北石油大学学报，2012，36（6）：76-81.Ren Junjie，Guo Ping，Wang Delong，et al.Productivity model of fractured horizontal wells in shale gas reservoirs and analysis of influential factors［J］.Journal of Northeast Petroleum University，2012，36（6）：76-81.