基于孔隙曲折度与等效岩石元素理论的致密砂砾岩导电模型
宋延杰,胡 凯,唐晓敏,侯 琳,王 超
(1.东北石油大学地球科学学院,黑龙江 大庆 163318; 2.东北石油大学非常规油气成藏与开发省部共建国家重点实验室培育基地,黑龙江 大庆 163318; 3.中国石油长城钻探工程有限公司,辽宁 盘锦 124000)
0 引言
徐家围子深层致密砂砾岩储层岩性以砂砾岩为主,矿物成分以岩屑为主,岩屑成分复杂,其次为石英和长石,其孔隙度主要分布为1.1%~7.6%,平均孔隙度为3.1%,渗透率主要分布为(0.01~3.30)×10-3μm2,平均渗透率为0.82×10-3μm2,分选因数主要为1.0~4.0,平均分选因数为2.1,最大孔隙半径主要为0.03~5.32μm,平均最大孔隙半径为0.98μm.研究区岩性成分复杂、储层物性差、分选性差、非均质性强、孔隙结构复杂,给准确求取储层饱和度参数带来一定的困难.
为适应致密储层饱和度评价的需要,人们研究致密储层的导电规律及导电模型.周荣安[1]、李军、石玉江、吴浩、刘堂晏等[2-6]基于岩电实验研究致密储层的导电规律,结果表明致密储层的地层因素与孔隙度、电阻增大系数与含水饱和度在双对数坐标系下多表现为非线性关系,阿尔奇模型在致密储层含油气饱和度定量评价时存在一定的不适用性.郑庆林等[7]、张龙海、孙小平、李秋实等[8-10]建立变参数阿尔奇公式,在一定程度上可提高含水饱和度的求取精度,但改进的阿尔奇公式并未考虑复杂微观孔隙结构对岩石导电性的影响,导致在孔隙结构复杂的致密储层应用效果不理想.闫伟林等[11]针对中基性火山岩复杂的孔吼结构特征,将总孔隙度分为导电孔隙度与不导电孔隙度,引入孔隙空间连通因子,计算得到导电孔隙度;并利用并联导电理论建立基于导电孔隙的饱和度模型,该模型在非均质性较强的高孔喉比储层饱和度评价中取得较好的应用效果.宋延杰、Koelman J M V A、De Kuijper A、唐晓敏等[12-15]针对低孔渗储层复杂微观孔隙结构特征,利用有效介质对称导电理论引入渗滤速率与渗滤指数,分析各组分的连通状况、形状及结构特征等对岩石导电性的影响,建立低孔渗储层饱和度模型,取得较好的应用效果.殷树军[16]针对Y油田南一段储层含凝灰、孔隙结构复杂的特征,引入孔喉比与孔隙曲折度描述复杂孔隙结构对岩石导电性的影响,利用串联导电理论建立地层因素与孔喉比及孔隙曲折度之间的函数关系式;同时,利用岩电实验数据研究地层因素与凝灰含量之间的关系,从理论和实验验证胶结指数与凝灰含量之间存在一定关系,并可以利用凝灰含量间接反映孔吼结构的变化,建立含凝灰储层变参数阿尔奇饱和度模型.Herrick D C和Kennedy W D[17-19]在孔隙几何形态导电理论中,将岩石孔隙空间等效为横截面积变化的弯曲毛管,并引入几何因子描述孔隙弯曲程度、横截面积变化对岩石导电性的影响,用et描述由油气的进入引起地层水分布几何形态特征变化对岩石导电性的影响,建立孔隙几何形态导电理论,能够较好地描述复杂孔隙结构储层的导电规律.Shang B Z等[20-21]在等效岩石元素理论中将岩石等效为规则圆柱体,将岩石孔隙空间等效为大、小孔隙的串联,其中大孔隙主要反映孔腔大小,小孔隙主要反映吼道大小,并引入孔隙结构效率反映岩石孔隙孔腔和吼道比对导电性的影响,但该理论仅考虑孔腔和吼道比变化对岩石导电性的影响,忽略孔隙弯曲程度对岩石导电性的影响.
针对徐家围子地区深层致密砂砾岩储层非均质性强、孔隙结构复杂的储层特征,利用等效岩石元素理论分析不同孔腔和吼道体积比对储层导电性的影响,并引入孔隙曲折度阐述孔隙弯曲程度对岩石导电性的影响,建立一种新的基于孔隙曲折度与等效岩石元素理论的致密砂砾岩储层导电模型.利用徐家围子地区深层致密砂砾岩储层岩电实验数据确定模型参数,并从实验精度分析及实际资料处理效果等方面评价该模型在致密砂砾岩储层中的适用性.
1 等效岩石元素理论
等效岩石元素理论将饱含水纯岩石孔隙空间等效为平行于电流流动方向的小孔隙(VPf),以及垂直于电流流动方向的大孔隙(VPp)两部分的串联,将小孔隙体积与大孔隙体积之比定义为孔隙结构效率eps,其等效体积模型和等效电路见图1(a)、(b)[20-22].
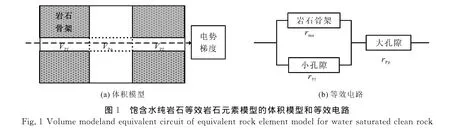
根据等效电路图,利用串并联导电理论可以推导出饱含水纯岩石的地层因素F为

式中:R0为饱含水岩石电阻率;Rw为地层水电阻率;φ为有效孔隙度.
当孔隙空间中存在油气时,含油气纯岩石等效岩石元素模型的体积模型及其等效电路见图2(a)、(b)[21-22].

根据含油气纯岩石的等效电路图,利用串并联导电理论可以推导出含油气纯岩石的视地层因素Fw为

式(2-3)中:epsw为水的孔隙结构效率,无量纲;r为非均匀因数;Sw为含水饱和度.
2 致密砂砾岩导电模型
等效岩石元素理论将孔隙空间等效为孔隙横截面积变化的直毛管,这种等效是对实际孔隙空间的一种简化,对于孔隙结构复杂的岩石,其孔隙空间等效为孔隙横截面积变化的弯曲毛管更合理.基于孔隙结构复杂岩石的孔隙空间等效为孔隙横截面积变化的弯曲毛管观点[18],对等效岩石元素理论进行改进,建立一种基于孔隙曲折度概念与等效岩石元素理论的致密砂砾岩储层导电模型.

2.1 饱含水
由于研究区致密砂砾岩泥质体积分数小于5%,可以不考虑泥质附加导电对致密砂砾岩导电性的影响,将饱含水致密砂砾岩等效为规则纯岩石圆柱体,等效体积模型见图3.设岩石的横截面积为A,长度为L;小孔隙的横截面积为A1,长度为L1;大孔隙的横截面积为A2,长度为L2,并设L2=CL1,A2=X2A1,其中A2=A,C、X 为因数.
若岩石骨架相不导电,则饱含水纯岩石的电阻等于含水大、小孔隙电阻串联之和:

根据孔隙结构效率eps和孔隙曲折度τ的定义,有
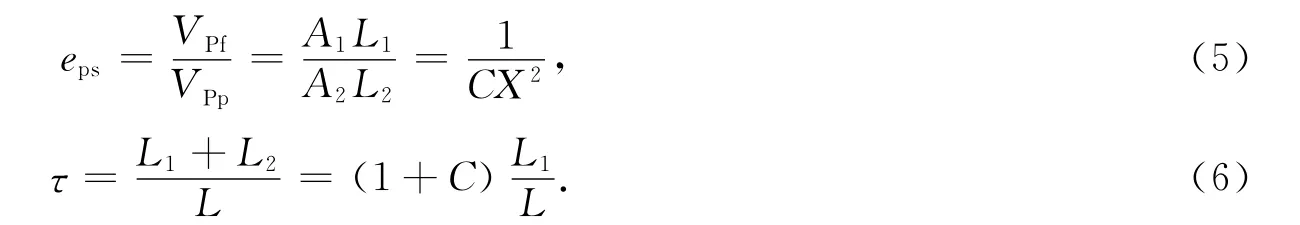
将式(5)、(6)代入式(4),地层因素F 可以表示为

2.2 含油气
当岩石中存在油气时,其等效体积模型见图4(a).设小孔隙含水横截面积为A1w,长度为L′1;大孔隙含水横截面积为A2w,长度为L′2,并设L′2=C′L′1,A2w=X′2A1w,其等效电路图见图4(b)[22].
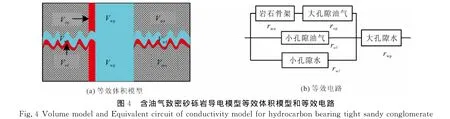
当岩石中存在油气时,假设油气在大、小孔隙中是均匀分布的,大、小孔隙的含水体积分别为A2L2Sw、A1L1Sw.然而油气在大、小孔隙中分布不均匀,引入非均匀分布因数r,并假设其中k为非均匀分布指数,小孔隙的含水饱和度为rSw,大、小孔隙中含水体积分别为

水的孔隙结构效率epsw为
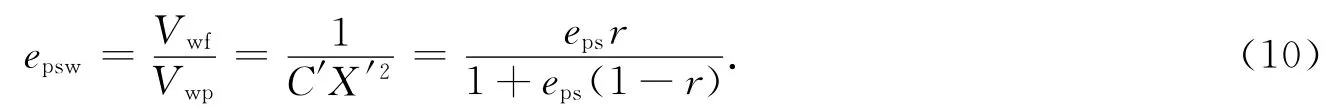
由于油气存在,使得岩石孔隙空间中水的导电路径更加弯曲,其等效孔隙曲折度τ′为
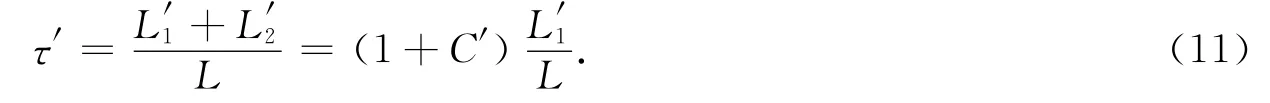
根据其等效电路图,有

其中
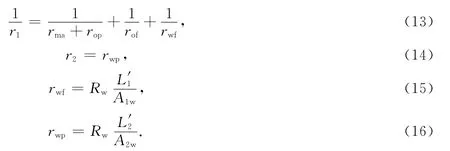
骨架和油气不导电,将式(13-16)代入式(12),整理得

式中:Rt为含油气岩石的电阻率.
由岩石含水孔隙体积等于大、小孔隙含水体积之和,有

将式(10)、(18)代入式(17),整理得
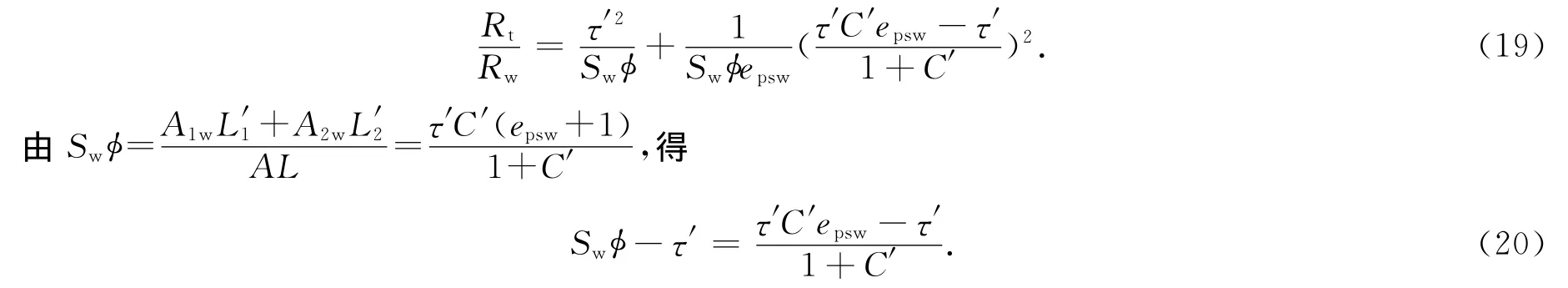
将式(20)代入式(19),可推出含油气岩石的视地层因素Fw:
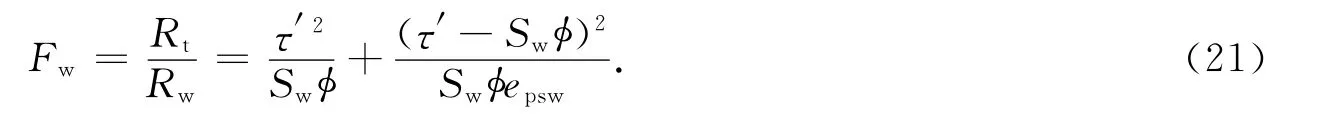
由于油气的存在致使孔隙空间中水的导电路径更加弯曲,并且随着含水饱和度的减小,其导电路径弯曲程度增加,故假设,其中n为孔隙中存在油气时等效孔隙曲折度随含水饱和度变化的指数,将τ′、epsw代入式(21),得
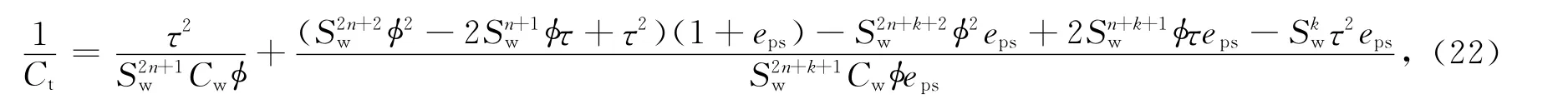
式中:Ct为岩石电导率;Cw为地层水电导率.
3 模型实验
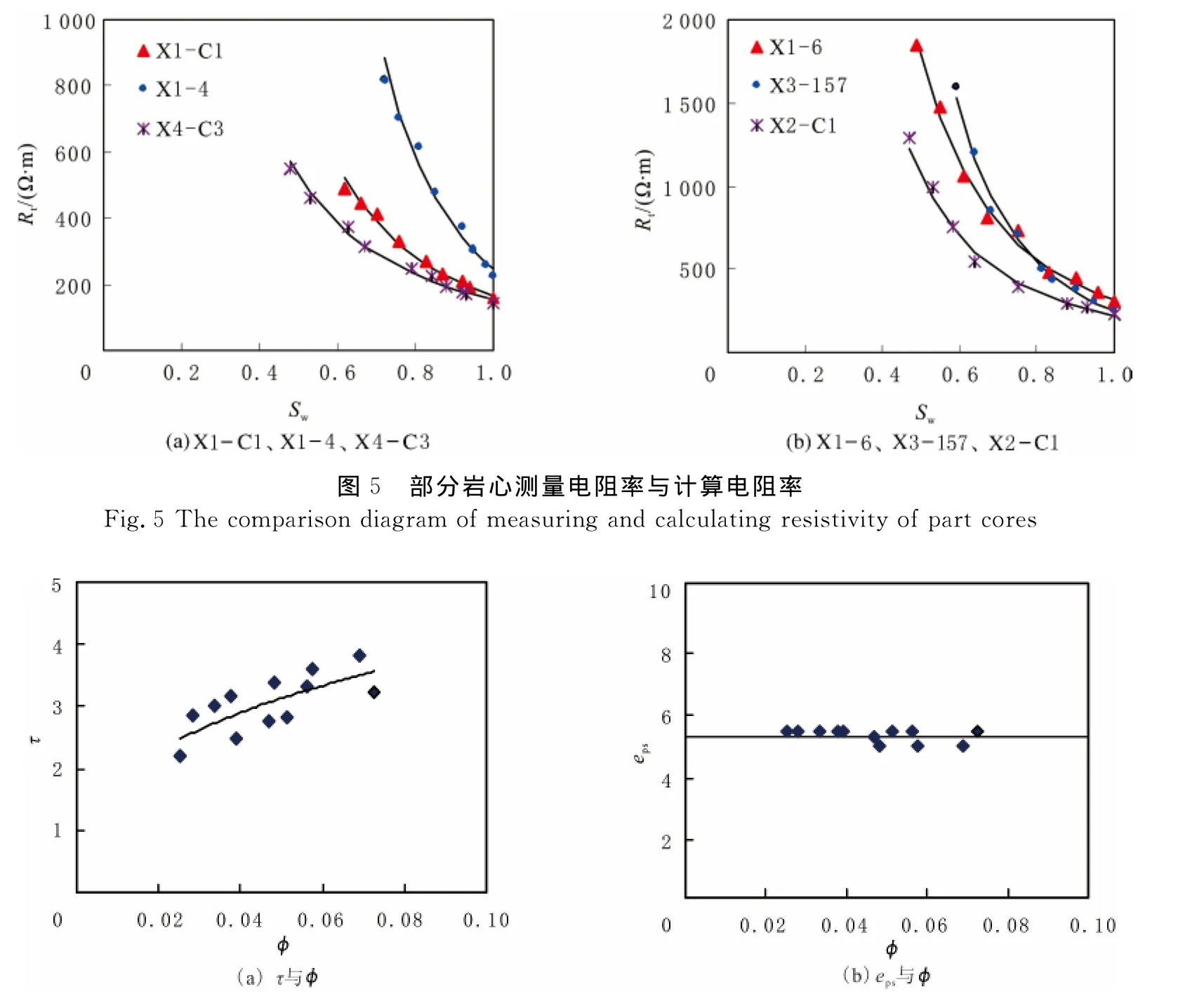
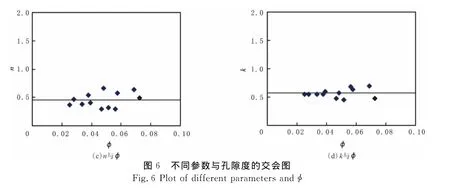
利用研究区4口井12块岩样岩电实验数据,采用最优化算法求解Ct-Cw-Sw的非相关函数,可以得到参数τ、eps、n、k值(见表1).部分岩样导电模型计算的电阻率值与岩心测量电阻率的结果见图5.由图5可以看出,该模型计算的电阻率值和实验测量电阻率基本吻合,平均相对误差仅为6.2%,表明该模型能够较好地描述致密砂砾岩储层的导电规律.各参数与孔隙度的交会图见图6(a-d).由图6(a-d)可以看出,τ与孔隙度存在一定关系,其关系式为τ=8.680 3×φ0.3403,eps、n、k与孔隙度无明显关系,且其变化范围较小,故取均值作为模型参数值,其中eps=5.30,n=0.45,k=0.57.

表1 致密砂砾岩导电模型的优化参数Table 1 Optimized values of parameters of conductivity model for tight sandy conglomerate
4 应用效果
利用基于孔隙曲折度与等效岩石元素理论建立的致密砂砾岩导电模型,对徐家围子地区深层致密砂砾岩储层的徐深A井和B井进行实际资料处理,并对比处理结果与试油结果.
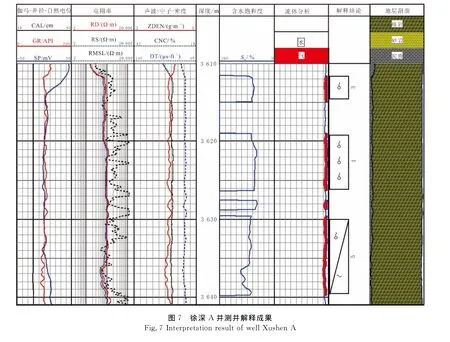
徐深A井的测井解释成果见图7.该井的试油深度段为3 613~3 641m,3、4、5号层合试,试油结果为产气量68 502m3/d、产水量4.8m3/d.利用建立的饱和度模型计算3、4号层含气饱和度大于60%,综合解释为气层;5号层的上部含气饱和度为60%左右,下部为40%左右,综合解释为气水同层.3、4、5层解释结果与试油结果吻合.
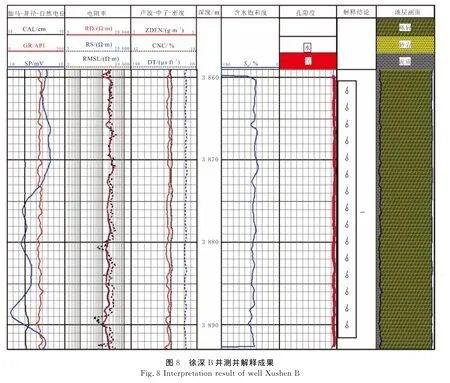
徐深B井的测井解释成果见图8.该井处理的1号层为试油层位,试油结果为产气量15 276m3/d.利用建立的饱和度模型计算1号层的含气饱和度大于60%,解释为气层.该层的解释结果与试油结果吻合.
徐深A、B井的测井解释结果与试油结果吻合较好,表明基于孔隙曲折度与等效岩石元素理论建立的致密砂砾岩导电模型适用于研究区致密砂砾岩储层评价.
5 结论
(1)基于孔隙曲折度与等效岩石元素理论建立的致密砂砾岩储层导电模型,既考虑孔隙孔腔和吼道比对储层导电性的影响,又考虑孔隙弯曲程度对岩石导电性的影响,该模型更适用于储层物性差、分选性差、非均质性强、孔隙结构复杂的致密砂砾岩储层.
(2)利用研究区的岩电实验数据通过最优化技术确定孔隙曲折度、孔隙结构效率等模型参数,对比该模型计算的岩样电阻率值与实验测量电阻率值,平均相对误差为6.2%,表明该模型能够较好地描述致密砂砾岩储层的导电规律.
(3)对研究区2口井进行实际资料处理,2口井含气饱和度大于60%,表明基于孔隙曲折度与等效岩石元素理论的致密砂砾岩导电模型能够准确求取储层含气饱和度,适用于徐家围子地区深层致密砂砾岩储层评价.
(References):
[1]周荣安.阿尔奇公式在碎屑岩储集层中的应用[J].石油勘探与开发,1998,25(5):80-82.Zhou Rongan.The application of Archie equation to the evaluation of clastic reservoirs[J].Petroleum Exploration and Development,1998,25(5):80-82.
[2]李军,张超谟,唐文生,等.库车地区致密砂砾岩胶结指数m和饱和度指数n的主要影响因素及其量化研究[J].石油天然气学报,2009,31(6):100-103.Li Jun,Zhang Chaomo,Tang Wensheng,et al.Major influtial factor and quantitative study on mexponent and nexponent in Kuche region[J].Journal of Oil and Gas Technology,2009,31(6):100-103.
[3]石玉江,李高仁,周金昱.泥质型低渗砂岩储层岩电性质研究及饱和度模型的建立[J].测井技术,2008,32(3):203-206.Shi Yujiang,Li Gaoren,Zhou Jinyu.Study on litho-electric character and saturation model of argillaceous low-permeability sandstone reservior[J].Well Logging Technology,2008,32(3):203-206.
[4]吴浩,郭英海,张春林,等.致密油储层微观孔吼结构特征及分类——以鄂尔多斯盆地陇东地区三叠统延长组长7段为例[J].东北石油大学学报,2013,37(6):12-17.Wu Hao,Guo Yinghai,Zhang Chunlin,et al.Characteristics and classifications of micro-pore structure in tight oil reservior:A case study of the Trias-sic Yanchang formation Chang7in longnan area,Ordos basin[J].Journal of Northeast Petroleum University,2013,37(6):12-17.
[5]刘堂晏,汤天知,杜环虹,等.考虑储层孔隙结构的岩石导电机制研究[J].地球物理学报,2013,56(8):2818-2826.Liu Tangyan,Tang Tianzhi,Du huanhong,et al.Study of rock conductive mechanism based on pore structure[J].Chinese Journal of Geophysics,2013,56(8):2818-2826.
[6]石玉江,时卓,张海涛,等.苏里格气田致密气层测井精细建模方法[J].西南石油大学学报,2012,34(5):71-77.Shi Yujiang,Shi Zhuo,Zhang Haitao,et al.Fine logging interpretation method of tight gas reservoir in Sulige gas field[J].Journal of Southwest Petroleum University,2012,34(5):71-77.
[7]郑庆林,王钰森,赵雨.低孔隙度条件下阿尔奇含水饱和度解释模型改进[J].测井技术,2006,30(1):57-59.Zheng Qinglin,Wang Yusen,Zhao Yu.Improvement of Archie water saturation method for the low porosity formation[J].Well Logging Technology,2006,30(1):57-59.
[8]张龙海,周灿灿,刘国强,等.孔隙结构对低孔低渗储集层电性及测井解释评价的影响[J].石油勘探与开发,2006,33(6):671-676.Zhang Longhai,Zhou Cancan,Liu Guoqiang,et al.Influence of pore structure on electric properties and well logging evaluation in low porosity and permeability reservoirs[J].Petroleum Exploration and Development,2006,33(6):671-676.
[9]孙小平,石玉江,姜英昆.复杂孔隙结构储层含气饱和度评价方法[J].天然气工业,2000,20(3):41-43.Sun Xiaoping,Shi Yujiang,Jiang Yingkun.Method of evaluation gas saturation in the reservoir with complicated pore structure[J].Natural Gas Industry,2000,20(3):41-43.
[10]李秋实,周荣安,张金功,等.阿尔奇公式与储层孔隙结构的关系[J].石油与天然气地质,2002,23(4):364-367.Li Qiushi,Zhou Rongan,Zhang Jingong,et al.Relations between Archie's formula and reservoir pore structure[J].Oil &Gas Geology,2002,23(4):364-367.
[11]闫伟林,覃豪,李洪娟.基于导电孔隙的中基性火山岩储层含气饱和度解释模型[J].吉林大学学报,2011,41(3):915-920.Yan Weilin,Qin Hao,Li Hongjuan.Study on the gas saturation computation method of neutral and basic volcanic rocks reservoir based on the conductive pore[J].Journal of Jilin University,2011,41(3):915-920.
[12]宋延杰,王海琦,唐晓敏,等.南海东部低孔低渗储层测井评价方法[J].大庆石油学院学报,2010,34(6):106-109.Song Yangjie,Wang Haiqi,Tang Xiaomin,et al.Logging evaluation of low porosity and permeability reservoirs in the east of South Sea of China[J].Journal of Daqing Petroleum Institute,2010,34(6):106-109.
[13]Koelman J M V A,De Kuijper A.An effective medium model for the electric conductivity of an n-component anisotropic percolating mixture[J].Physica A,1997,247:10-22.
[14]De Kuijper A,Sandor R K J,Hofman J P,et al.Electrical conductivities in oil-bearing shaly sand accurately described with the satori saturation model[J].The Log Analyst,1996:22-31.
[15]唐晓敏,宋延杰,张传英.低阻油层通用有效介质对称电阻率模型的应用[J].大庆石油学院学报,2008,32(2):18-22.Tang Xiaomin,Song Yangjie,Zhang Chuanying.Application of generalized symmetrical effective medium resistivity model in low resistivity reservoir[J].Journal of Daqing Petroleum Institute,2008,32(2):18-22.
[16]殷树军.含凝灰储层原始含油饱和度测井评价方法探讨[J].测井技术,2014,38(1):69-72.Yin Shujun.On log evaluation method of oil saturation in tuffaceous resevoir[J].Well Logging Technology,2014,38(1):69-72.
[17]Herrick D C,Kennedy W D.Electrical efficiency—A pore geometric theory for interpreting the electrical properties of reservior rocks[J].Geophysics,1994,59(6):918-927.
[18]Herrick D C,Kennedy W D.A new look at electrical conduction in porous media:A physical description of rock conductivity[C].Texas:The SPWLA 50th Annual Logging Symposium,2009.
[19]Kennedy W D.The porosity-water saturation-conductivity relationship:An alternative to Archie's model[J].Petrophysics,2007,48(5):335-361.
[20]Shang B Z,Hamman J G,Caldwell D H.A physical model to explain the first Archie relationship and beyond[C].Denver:SPE Annual Technical Conference and Exhibition,2004.
[21]Shang B Z,Hamman J G,Caldwell D H.Improved water saturation estimation using equivalent rock element model and application to different rock types[C].Rome:SPE Europec/EAGE Annual Conference and Exhibition,2008.
[22]宋延杰,杨汁,刘兴周,等.基于有效介质与等效岩石元素理论的特低渗透率储层饱和度模型[J].测井技术,2014,38(5):510-516.Song Yanjie,Yang Zhi,Liu Xingzhou,et al.A saturation model for ultra-low permeability reservoirs based on the effective medium conduction theory and equivalent rock element theory[J].Well Logging Technology,2014,38(5):510-516.

