混合风电场中PMSG协助感应发电机低电压穿越
李生虎,安 锐 ,许志峰,董王朝
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009;2.国家电网江西省电力公司检修分公司,江西 南昌 330029)
0 引言
低电压穿越(LVRT)是风电并网的基本要求之一[1-3]。在外网故障下,希望风电机组保持并网,提供无功支持以维持电压[4-5],缩短故障后恢复过程。
感应发电机(IG)结构和控制简单[6-7],在早期风电建设中广为应用。但是其从电网吸收无功,为避免故障期间滑差失稳[8],需要增加并补设备或串联制动电阻[9-10],从而增加投资。因此目前新建风电机组多为双馈和直驱型机组[11-13],与现有IG机组一起,形成混合风电场。
对于直驱永磁同步发电机(PMSG),通过在直流侧加入卸荷电路或储能装置[14-15]可以实现LVRT。网侧变流器(GSC)无功出力有助于维持电压和减少事故后恢复时间[16]。PMSG富余无功容量可提高公共连接点(PCC)电压,有可能帮助同一风电场内相近IG机组故障穿越,避免新增投资。
对于利用PMSG协助IG LVRT问题,文献[17-18]中PMSG故障期间没有向电网输送有功,未达到连续供电的要求。文献[19-20]在故障期间可以提供有功支持,但仿真故障尺度较短,不足以验证协同LVRT效果。文献[18-20]验证了给定台数时可以协同LVRT,但并未给出协同LVRT所需PMSG的最少容量或台数的定量算法。文献[17]给出了PMSG与IG的大致比例,但是仅通过动态仿真结果,没有定量算法,因此缺乏普遍应用价值。文献[6]提出计算IG临界切除时间的理论算法,但是由于取电网电压为零,计算过程虽然简单但是理想化。
针对包含PMSG和IG的混合风电场,本文研究了利用PMSG富余无功容量帮助IG LVRT的可行性,提出了帮助IG LVRT的PMSG最少台数的定量算法。首先将IG电磁转矩用电压和转差率的函数表示,根据转矩平衡关系,计算导致IG滑差失稳的临界转差率。将故障期间电磁转矩表示为PCC电压和转差率的函数,根据临界转差率和故障持续时间,对转矩平衡方程积分,得到IG不失稳时PCC临界电压。根据PCC到电网间电压降落关系,得到将PCC电压提高到临界电压所需增发无功。在保证PMSG自身LVRT前提下,通过改变GSC无功参考值予以实现。根据风电并网导则确定的最严重电压跌落场景,计算协助IG LVRT所需PMSG最少台数。文中给出动态仿真结果,验证了理论分析的有效性,分析了理论推导误差原因以及临界电压的影响因素。
1 PCC临界电压计算
图1为协同LVRT的风电系统结构,PMSG和IG分别通过升压变连接至PCC,然后并入电网。其中,1 端为电网;2 端为 PCC;U1、U2、I1、I2分别为电网和 PCC 处的电压、电流;XTA、XTB、XTC分别为变压器 TA、TB、TC电抗;RG、XG分别为 GSC 电阻和电抗;RL、XL分别为线路电阻和电抗;Rd为GSC直流侧卸荷电阻。令 X1=XL+XTC,R1=RL,Z=R1+jX1。
图2给出 IG 等值电路。 其中,RS、XS、RR、XR分别为定子和转子的电阻、电抗;XM为激磁电抗;s为转差率;IS为定子电流;IR为转子电流。令X=XS+XR+XTB。
基于戴维南定理,计算等值电压UTH和等值阻抗ZTH如下,其中 ZM=jXM,ZS=RS+jXS+jXTB。

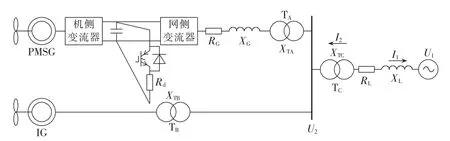
图1 混合风电场结构Fig.1 Configuration of hybrid wind farm

图2 IG等值电路Fig.2 Equivalent circuit of IG

IG电磁转矩TE表示为式(3)。由于sRTH远小于RR,可以忽略,TE简化为式(4)。
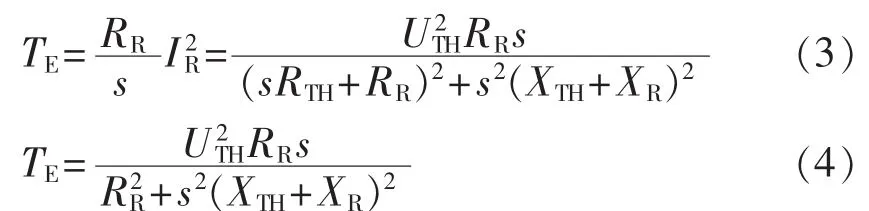
IG机械转矩TM为:
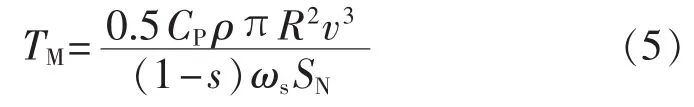
其中,ρ为空气密度;R为风轮机的半径;v为风速;CP为风电机组的风能利用系数;ωs为同步角速度标幺值;SN为基准容量。
传动系统采用单质量块模型,则转子运动方程为:

其中,HG、HM分别为发电机、风力机的惯性时间常数。
定义系数K1—K7,具体如下:
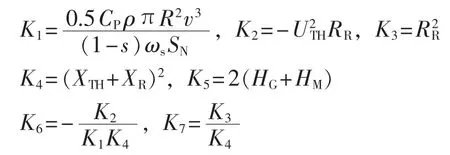
故障期间认为转差率和风能利用系数变化不大,近似认为 K1为常数,将式(4)和(5)代入式(6),则式(6)变为:
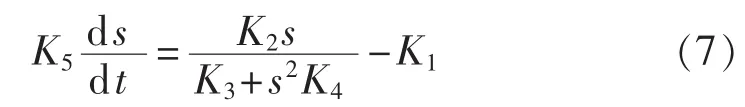
令式(7)等号左侧为0,得IG初始转差率s0和临界转差率 scrit[6]:
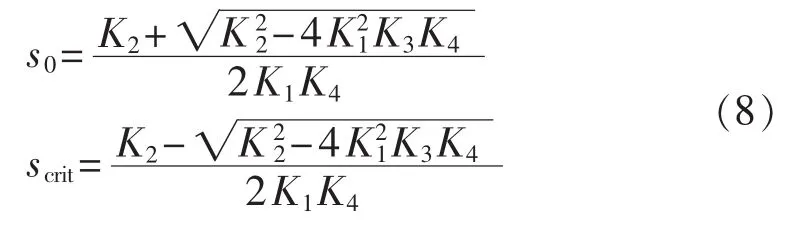
将带有s的项移到方程等号的左边,带有t的项移到方程等号右边。左边对s进行积分,积分区间为s0到scrit;右边对t进行积分,积分区间为故障时间tfault。左右两侧积分区间的含义为:转子转速从初始转差率s0加速到临界转差率scrit所用时间恰好为tfault。如果故障时间变长则IG滑差失稳。
当 K62<4K7时,得到式(9),其中 t1为故障结束时间。为了使计算得到的故障初始时间t0与实际发生故障的时间保持一致,引入积分常数C1,由于临界电压为从初始转差率到临界转差率积分之差,所以C1并不影响临界电压的计算。
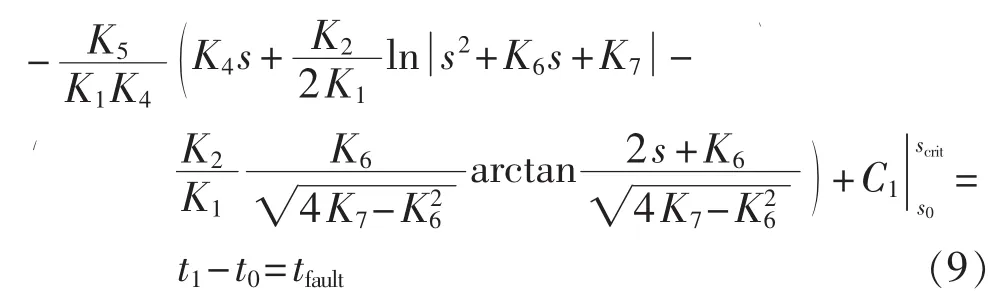
当 K62>4K7时,得到式(10),C2与 C1意义相同。由于 K2中包括 UTH,通过式(9)或(10)可确定给定故障时间内保证IG不失稳的PCC临界电压。

由以上推导可见,IG临界电压影响因素包括其惯性时间常数、临界转差率、转矩不平衡量以及故障持续时间。
2 协同LVRT所需PMSG台数
由于GSC容量限制,每台PMSG可增发无功是有限的。根据最严重电压跌落场景,计算将PCC电压提高到临界电压所需的最少无功,进而可确定所需PMSG最少台数。
电网故障时,GSC电流参考值控制策略如图3所示。其中,Udc为直流母线电压;Qgrid为PCC处无功功率;Igd、Igq分别为GSC的d轴和q轴电流;上标*表示参考值。为使故障期间仍能对电网提供有功支持,取GSC最大电流为Ilim,分解到q轴限幅为Igqlim。故障期间为尽可能地向电网输送无功以抬高PCC电压,重新设定GSC有功和无功电流参考值。无功电流参考值通过输向PCC无功功率PI调节器得到。通过比较直流电压PI调节器输出值和,得到最小值即为有功电流参考值。
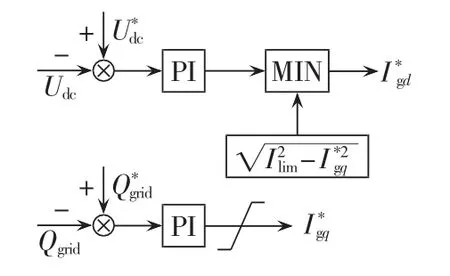
图3 GSC改进无功控制Fig.3 Enhanced var control of GSC
在同一风电场内,近似认为每台IG风速大致一致,将其等值为1台。当电网电压跌落时,假设故障期间IG的平均转差率为sC,则IG向PCC输送的有功PIG和无功QIG为:
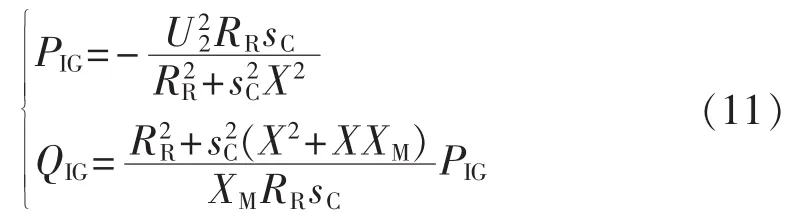
整个风电场输向PCC的有功P2和无功Q2为:

其中,PPMSG、QPMSG分别为每台PMSG输向 PCC的有功功率和无功功率;n为PMSG台数。

其中,U2d、U2q分别为PCC处d轴和q轴电压。采用电压定向d轴,U2d=U2,U2q=0。认为故障期间,总电流和q轴电流都已达到幅值时,将其代入式(13)求取 PPMSG、QPMSG。
为实现PMSG和IG协同LVRT,首先要保证PMSG自身LVRT,本文采用在直流侧增加卸荷电路的控制策略;其次要保证GSC容量限制,忽略GSC出线有功损耗,将 PPMSG、QPMSG代入式(14)、(15)保证其成立。
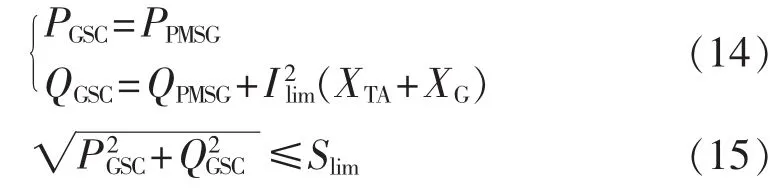
其中,PGSC、QGSC分别为GSC输出的有功功率和无功功率;Slim为GSC的最大容量。
当电网电压跌落时,将PCC电压抬高到其临界电压,所需PMSG台数由PCC处功率决定。此时已知电网电压和PCC功率,求取PCC电压。为避免迭代,建立以下直接求解算法:

其中,a11、a12、a21、a22为相应矩阵元素。令:

其中,d1、d2为常数;θ为式(18)中第一个方程等式左侧量的相角;S*2=-(P2-jQ2)。

将 P2、Q2代入式(19)、(20),计算将 PCC 电压抬高到临界电压所需的PMSG台数n。显然,临界电压越低,所需无功容量越小,PMSG台数越少。
本文在保证PMSG自身LVRT的条件下协助IG LVRT。在故障期间,PMSG输出有功不变。通过抬高机端电压避免IG滑差失稳,IG输出有功增大,从而整个风电场有功输出增加。
协同LVRT的临界条件取决于PCC的临界电压、GSC的极限容量以及PMSG的LVRT控制策略。由于IG的机械转矩越大,故障持续时间越长,IG越容易失稳,所以本文计算了IG在额定运行情况下按照并网导则规定的故障时间下PCC的临界电压。在额定运行方式下,GSC富余容量最小,协助IG LVRT能力最弱,所以由此计算的PMSG台数可以满足其他运行方式下协同LVRT。
本文没有改变PMSG原有撬棒控制,只是通过控制PMSG发出无功功率来抬高PCC电压确保IG成功穿越,而IG滑差失稳只与端电压有关,因此没有考虑IG和PMSG撬棒控制的协调性。更深一层考虑,将同时协调有功和无功优化,其中有功控制包括正常有功出力控制和故障时撬棒控制,但是解决方案尚未确定。从PMSG安全角度考虑,撬棒控制优先程度高于帮助IG LVRT,两者不便统一协调优化。
3 仿真分析
风电场中IG为10台,参数为:RS=0.0121 p.u.,XS=0.0742 p.u.,RR=0.008 p.u.,XR=0.1761 p.u.。 XM=2.7626 p.u.,HG=0.5 s,HM=2.5 s。 PMSG 参数:磁通 φ=1.4 p.u.,d 轴电抗 Xd=1 p.u.,q 轴电抗 Xq=0.7 p.u.,RG=0.02 p.u.,XG=0.02 p.u.,Rd=6 p.u.。 变压器参数:XTA=XTB=0.08p.u.,X1=0.005 p.u.,R1=0.0005 p.u.。Ilim=1.6 p.u.,Igqlim=1.55 p.u.,Slim=1.6 p.u.,sC=-0.05。 单台IG与PMSG的额定容量均为1 MW。基准功率取1 MW。初始时刻,PMSG和IG均运行在额定情况下。按我国风电并网导则要求,最严重情况下电网电压跌至0.2 p.u.,持续时间0.625 s。
3.1 理论推导结果
计算初始转差率和临界转差率,得到保证IG不失稳时PCC临界电压。然后为将PCC电压抬高到临界电压,计算所需PMSG台数。具体计算步骤如下。
额定情况下,通过PMSG无功补偿使得PCC电压为 1.05 p.u.,来保证 IG 机端正常电压接近 1 p.u.,IG额定机械转矩为1 p.u.。通过式(8)得到初始转差率s0和临界转差率scrit:

将初始转差率s0和临界转差率scrit代入式(9),得:

得到保证IG不失稳时PCC临界电压U2为0.62 p.u.,满足K26<4K7的条件。然后求取故障期间每台PMSG和所有IG的有功和无功出力:

当电网电压跌落至 0.2 p.u.时,可得 d1=0.2 p.u.,此时有:

为了将PCC电压U2抬高到其临界电压,计算所需 PMSG 台数,将 d2r和 d2i代入式(19),得到所需PMSG台数为70台。

以下进行动态仿真分析,以检验理论推导结果的正确性。
3.2 IG失稳临界电压
取 PCC 电压分别为 0.59 p.u.和 0.58 p.u.,图4给出IG转子转速ωr(标幺值,后同)的变化情况。当PCC电压为 0.59 p.u.时,故障期间转子转速增大,故障结束后由于定子电流和转子电流很大,机端电压不能瞬时恢复到故障前的值,此时机械转矩仍大于电磁转矩,转子继续加速。经过振荡机端电压逐渐恢复到故障前的值,转子逐渐减速,最后恢复正常转速。当PCC 电压为 0.58 p.u.时,故障期间转子加速,故障结束时转子转速大于临界转速,故障恢复后转子一直加速,机械转矩始终大于电磁转矩,IG滑差失稳。则临界电压为 0.59 p.u.,与理论计算值误差 0.03 p.u.,误差原因在于实际机械转矩随着转差率的变化而改变。

图4 不同电压跌落时转速变化Fig.4 Rotor speed variation for different voltage drops
分别将IG惯性时间常数、转子电阻增加20%,机械转矩、定子电抗减小20%,故障持续时间缩短20%,图5给出了临界电压变化。
图5(a)—(c)中,IG 惯性时间常数、转子电阻增大,定子电抗减小,增加机组惯性或电磁转矩,转子加速变慢,所以临界电压分别减小到 0.54 p.u.、0.55 p.u.、0.54 p.u.。 图5(d)中,故障持续时间缩短,时间积分区间变小,转子加速时间变短,更难达到临界转差率,所以临界电压减小到0.48 p.u.。图5(e)中,机械转矩减小,转差率积分区间增加,机械转矩和电磁转矩差值变小,所以临界电压减小到0.22 p.u.。
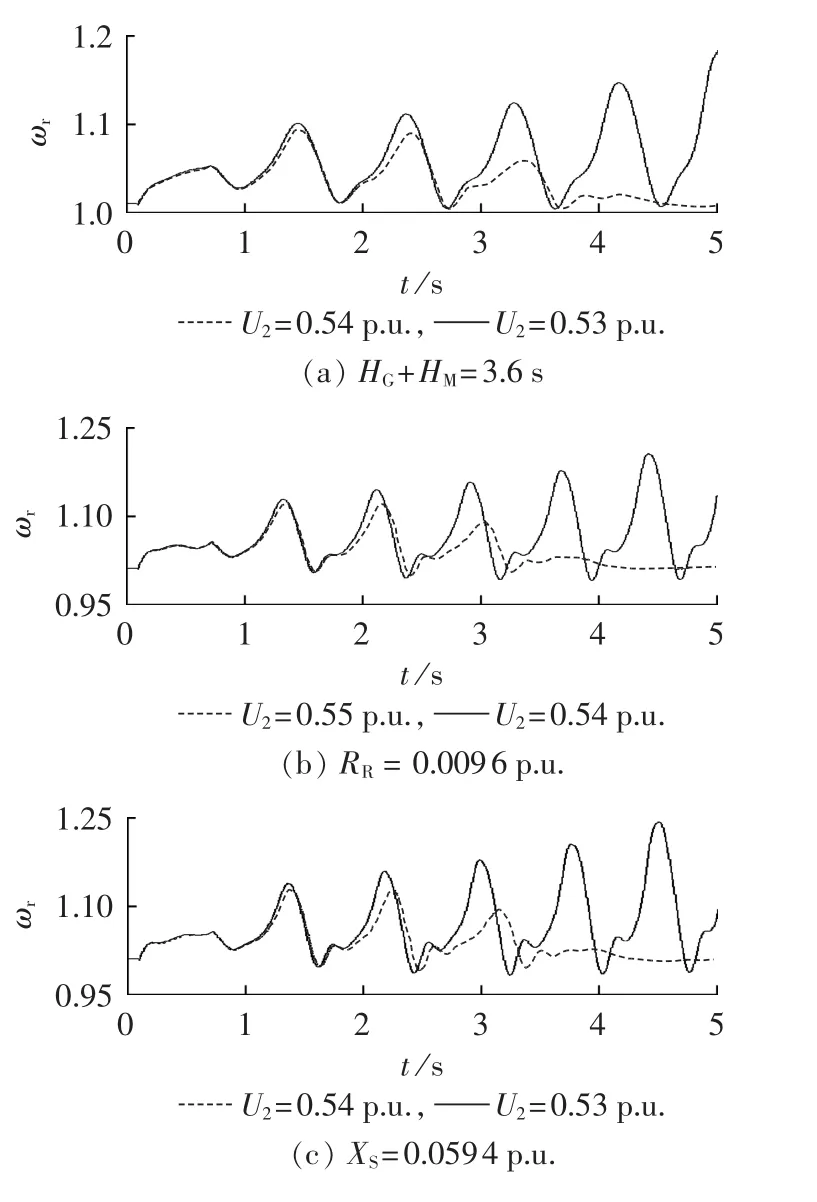
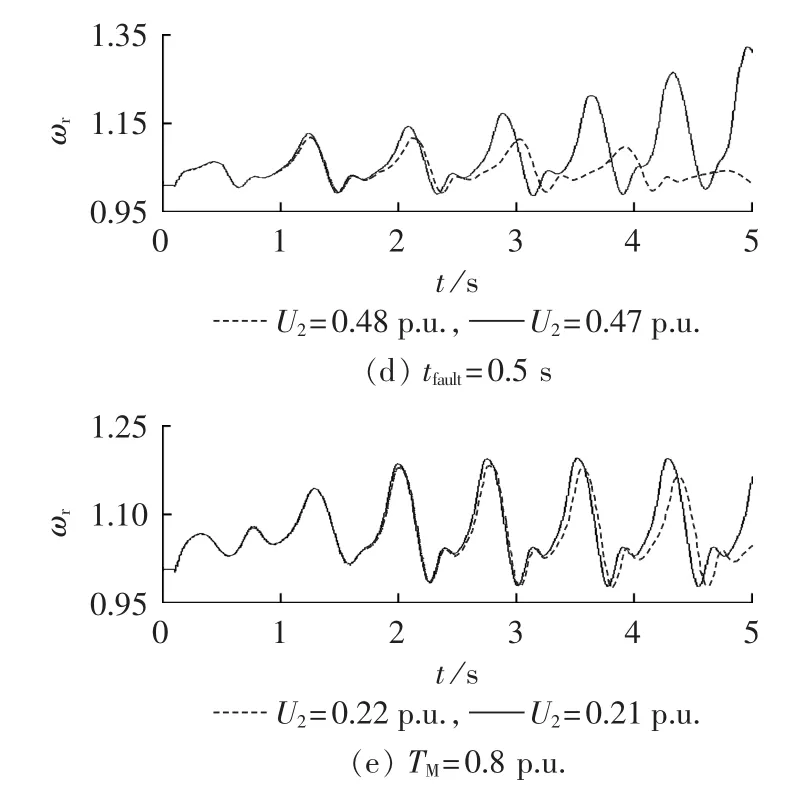
图5 临界电压影响因素Fig.5 Contributing factors to critical voltage
综上所述,IG惯性时间常数或转子电阻越大,IG机械转矩或IG定子电抗越小,故障时间越短,临界电压越低。对临界电压影响从大到小依次为IG机械转矩、故障时间、IG转子电阻、IG惯性时间常数和定子电抗。
3.3 协同LVRT所需PMSG台数
取PMSG不同台数,图6给出每台PMSG直流母线电压和输向PCC有功(标幺值),卸荷电阻投入避免了直流母线过电压,PMSG可以保证自身LVRT。

图6 PMSG LVRT效果Fig.6 LVRT effect of PMSG
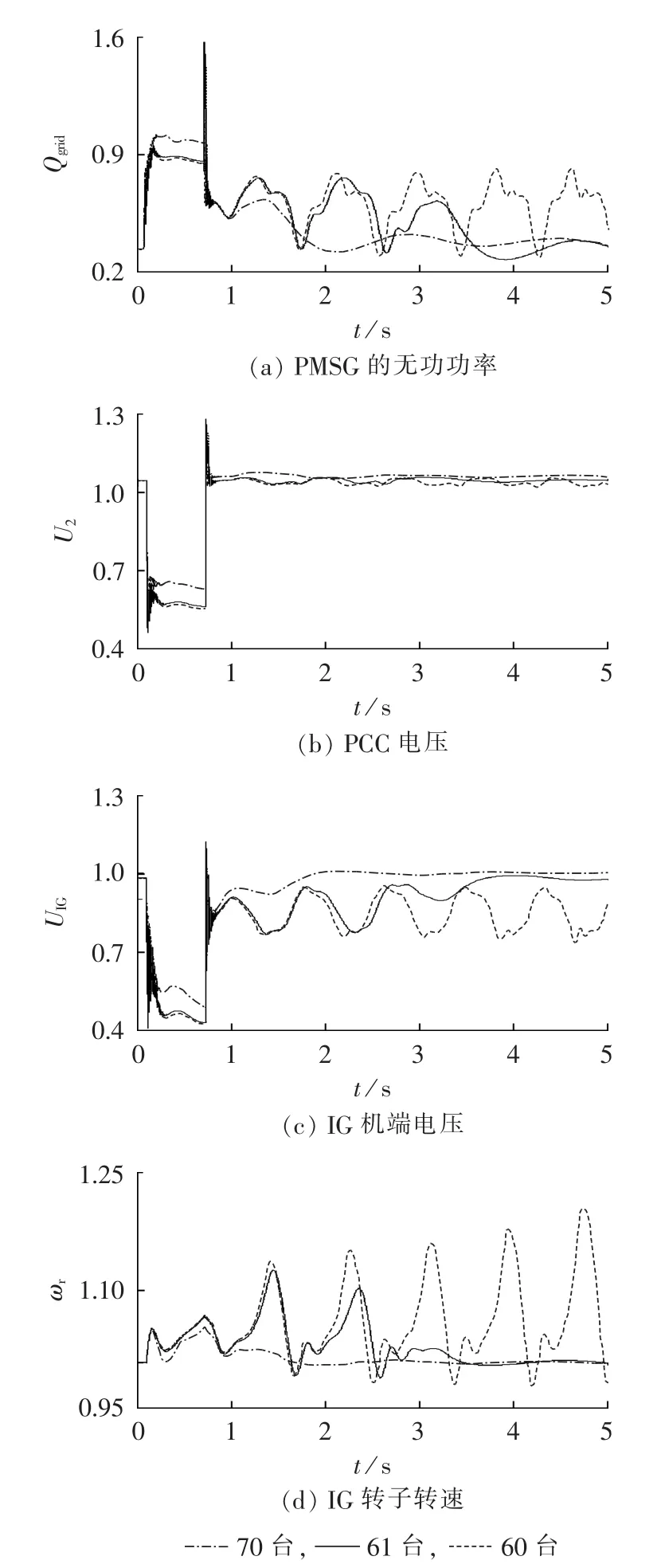
图7 PMSG协助IG LVRT效果Fig.7 Coordinated LVRT of IG and PMSG
图7给出了每台PMSG输向PCC无功、PCC电压、IG机端电压和转速(均为标幺值)曲线,以检验协同LVRT效果。故障期间,改变GSC无功参考值,增发无功功率抬高PCC电压、IG机端电压,减小IG转速上升速度,使得PCC电压大于临界电压以满足IG LVRT。
PMSG台数越多时,其无功功率、IG机端电压和转速恢复越快,协同LVRT效果越好。基于本文风电机组参数和控制策略,为保证IG LVRT,需要至少61台PMSG,即IG和PMSG台数比约为1∶7,可以保证IG和PMSG同时完成LVRT。PMSG最少台数略少于理论分析结果(70台),原因在于PCC临界电压估计值误差,以及电压跌落时IG出力和PCC电压的动态变化。
4 结论
针对包含PMSG和IG的混合风电场,研究了利用前者富余无功容量帮助后者LVRT的问题。按照风电并网导则规定最严重电压跌落下,计算保证IG LVRT所需无功容量,确定协同LVRT所需的PMSG台数。
算法推导和仿真分析得到以下结论:
a.PCC临界电压与机械转矩、IG参数以及故障持续时间有关,IG惯性时间常数或转子电阻越大,机械转矩或定子电抗越小,故障时间越短,临界电压越低;
b.对PCC临界电压影响从大到小依次为IG机械转矩、故障时间、IG转子电阻、IG惯性时间常数和定子电抗;
c.由于PCC临界电压估计值偏高,以及电压跌落时IG出力和PCC电压动态变化,使得理论分析得到的PMSG最少台数略高于实际所需台数,从而保留了一定裕度,有利于保证IG LVRT。

