风电接入后考虑抽蓄-需求响应的多场景联合安全经济调度模型
李 丹,刘俊勇,刘友波,高红均
(四川大学 电气信息学院,四川 成都 610065)
0 引言
含大规模风电的电力系统调度问题已成为备受关注的课题[1-3]。研究方法已逐步从传统电源调度方法的探索转化为新型高效调度资源与传统电源侧资源的整合。 其中,储能系统 ESS[4](Energy Storage System)和需求侧响应 DR[5](Demand Response)成为近来关注的焦点。
抽水蓄能是大规模储能技术中较为成熟且应用最广的技术之一。文献[6]提出风、火与抽蓄联合运行的模式,采用抽蓄电站为风电提供备用服务,以达到降低系统运行成本的目的;文献[7-9]对“风-蓄”协调及联合运营方式进行了讨论,以“风-蓄”整体效益最优为目标对联合运行模式进行优化。上述协调和联合模式在一定程度上解决了风电随机波动带来的问题,但是限制了抽蓄在调峰等其他方面的作用。相对于联合模式,文献[10]将抽蓄等效为“可中断负荷IL(Interruptible Load)”应用于系统调峰运行中,与火电、水电联合运行,获得了良好的效果;文献[11]利用鲁棒优化技术并结合风电不确定集合得到了抽蓄和机组的最佳运行模式,该模式能够在一定程度上接纳风电的随机波动并降低系统运行成本。
上述研究均将抽蓄纳入了系统调度优化模型中,并在考虑风电不确定性的条件下利用优化技术,达到了降低系统运行成本的目标。但抽水蓄能电站投资成本普遍较高,配置规模有限,在同时承担降低运行成本、备用成本和削峰填谷等任务时显得较为紧张。随着智能电网进一步发展,DR近年来成为学者较为关注的一种新型可调度资源[12]。
文献[12-13]将DR中的IL与用电激励负荷作为新型备用资源进行调度,达到了负荷侧参与调度减小备用成本的目的。文献[14]通过设计用户侧自愿申报用电意愿和移峰成本的新型互动调度模式,建立了能够反映用户意愿的互动负荷模型,并应用于机组组合之中;文献[15-16]以基于消费者心理学的分时电价用户响应原理预测的负荷曲线为基础并引入IL作为部分备用,考虑风电随机波动特性,对分时电价、可中断备用以及机组出力等进行了整体优化制定。上述工作通过不同的方式将DR引入电力系统调度之中,但移峰成本和基于心理学的分时电价模型与用户真实用电需求尚有一定偏差,且负荷的调用受到刚性用电需求限制,因此在某些时段和情况下无法大规模调用,限制了其调峰和提供备用的能力。
以上文献分别从抽蓄和DR两方面对风电接入后的电力系统调度问题进行了深入的探讨。本文在此基础上,结合两方面的经验,研究大规模风电接入后风-蓄-DR-火电力系统联合安全经济调度,将抽水蓄能和转移负荷对负荷曲线的优化作用与IL参与备用对系统经济性的提高融入同一模型。计及IL容量和电量成本,并为转移负荷设计了二维阶梯交叠式负荷转移成本申报函数。结合基于预测和随机场景的成本评估技术,建立以调度总成本最低为目标的调度模型。通过对比多种策略下的调度结果,验证了联合模式的经济性。
1 DR模型
1.1 DR互动机制
基于激励的DR包括IL和可转移负荷TL(Transfer Load)。考虑负荷转移时间LTT(Load Transfer Time)与负荷转移电量LTP(Load Transfer Power)对于用户生产经营的影响,设计了LTT和LTP的二维阶梯交叠式负荷转移成本申报函数,IL采用容量和电量双补偿机制,用于评估调用效率,避免过多的调而不用现象产生。用户侧综合考虑各项成本及收益后,调整自身用电需求或生产计划,自愿申报IL和TL函数。电网公司将DR与传统发电资源连同抽蓄一并视为可调度资源并综合考虑风电不确定性进行统一调度。
1.2 负荷转移成本模型
LTT与LTP对于用户用电或生产都有一定的影响。在充分考虑用户参与的灵活性后,设计如下二维阶梯交叠式负荷转移成本申报函数。
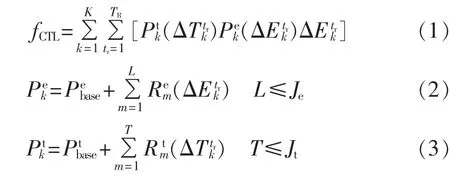
其中,K为提供转移的用户总数;TR为某一用户所提供的负荷序列总和;分别为转移电量和转移时间;分别为转移电量与转移时间的成本函数;Pebase、Pbtase分别为转移能量与转移时间的基础价格;Rem(ΔEktr)与 Rmt(ΔTtkr)分别为用户根据自身实际情况,在基础价格上制定的能量和时间的阶梯价格增量;m为转移量与转移时间所处时间段位;L、T为调用段位数;Je与Jt为总段位数。
成本函数示例见图1,负荷转移成本随着负荷转移量与转移时间增加而增加,这种将转移时间和转移电量分别补偿的方法,能够使用户选择更加灵活,调度中心汇总各个负荷转移成本信息后,调度也更加便捷;同时,用户自由选择各阶段价格,充分体现了用户参与的意愿。图中各段位成本增量较为平均,在实际情况下,随着时间或电量的增加,各段位成本都会加速增加。
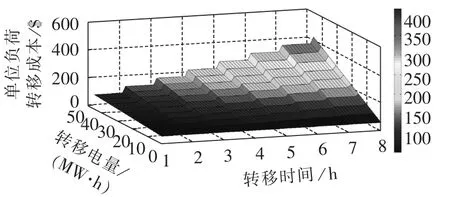
图1 单位负荷转移成本函数示例Fig.1 Example of unit load transfer cost function
1.3 IL成本模型
IL在系统峰荷或故障时,可以减少负荷需求量,等效增加备用容量,因此可减少系统对传统备用的容量需求和发电厂扩建巨额投资成本,并能快速响应、实时跟踪风功率变化,体现了用户互动意愿、引导科学用电。IL成本模型分为容量和电量两部分,数学模型如下[17]:
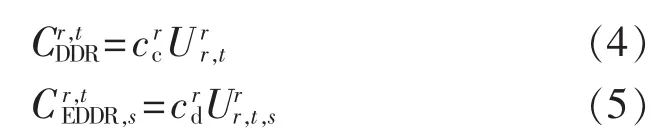
其中,ccr和cdr分别为用户r的IL容量和电量价格,价格体系和申报机制与TL类似;Urr,t、Urr,t,s分别为用户r在t时段提供的容量和在场景s下调用的电量。
2 联合安全经济调度模型
本文所提模型基于预测和随机场景两部分,获取某种调度决策后,两部分分别进行如第3节所述的成本评估。第一部分的变量为火电机组状态及出力、备用安排,抽蓄机组状态及出力,负荷转移电量和时段,IL容量;第二部分变量为不同场景下的备用及可中断调用情况以及意外弃风和失负荷量。
2.1 目标函数
定义目标函数如下:

其中,F(·)、Fre(·)分别为燃料成本和备用成本函数;Pit为机组i在t时段的出力;SUit、SDit分别为火电机组i在t时段的开、停机费用;Ruit、Rdit分别为机组 i在 t时段的上、下旋转备用容量;Rits为场景s中被调用的火电机组备用;γ为意外失负荷的惩罚系数;LDs为场景s下意外失负荷量;Pcurt,wts为场景 s下的弃风惩罚;Ccurt,wts为场景 s 下的弃风量;ps为场景 s 发生的概率;NT为调度周期总时段数;NG、Nh、Nr、Nw分别为火电机组、抽蓄机组、可中断用户以及风电场总数;Ns为风电出力场景数分别为抽水蓄能机组h在t时段的启、停费用。目标函数中为预测场景的发电、启、停以及备用容量成本;)为抽蓄机组启停成本;fCTL为负荷转移成本;为 的容量成本IL;为场景s中机组旋转备用调用、IL调用、意外失负荷和意外弃风成本。
2.2 约束条件
本文在考虑了火电机组、抽蓄和IL各项技术约束基础上,针对电网实际安全需求,加入N-1安全约束和备用调用有效性约束,有效保障了系统运行安全,具体约束如下。
a.功率平衡约束:
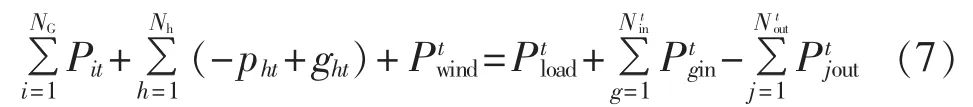
其中,pht、ght分别为抽水蓄能机组h在t时段抽水储能和放水发电时的功率值;分别为 t时段风电、负荷预测值;Pgtin、Pjtout分别为t时段转移入的负荷功率和转移出的功率值;Nitn、Notut分别为相应参与用户总数。
b.各机组出力约束:

其中,Pmin,i、Pmax,i分别为火电机组i的出力下限和上限;gmax,h、gmin,h和pmax,h、pmin,h分别为抽水蓄能机组h的发电及抽水功率上、下限。
c.火电机组爬坡率约束:
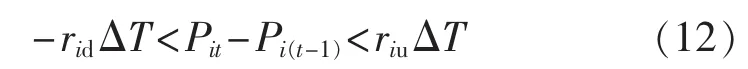
其中,rid、riu分别为机组i上、下爬坡速率;ΔT为相邻时间段的时间间隔。
d.火电机组启停时间约束:
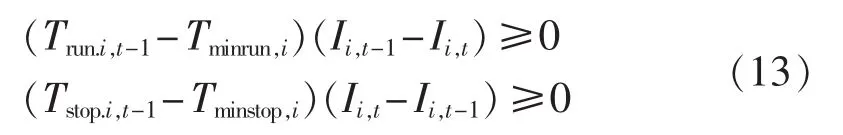
其中,Trun.i,t-1、Tstop.i,t-1分别为 t-1 时段火电机组 i的连续运行时间和停运时间;Ii,t为火电机组启停状态变量,为 1 表示启动,为 0 表示停机;Tminrun,i、Tminstop,i分别为火电机组i的最小运行和最小停运时间。
e.备用约束:

其中,Rut和 Rdt分别为 t时段正、负备用需求;LDRRmax,r为IL备用上限。式(14)、(15)为常规机组上、下备用约束;式(16)、(17)分别为上、下备用总量约束;式(18)为IL备用约束。
f.抽水蓄能库容约束:
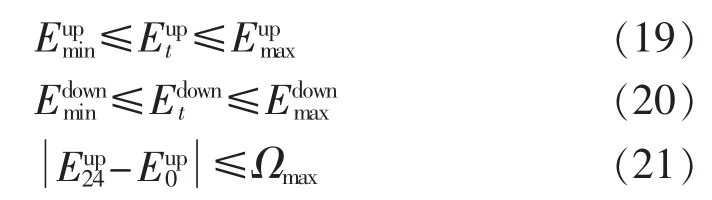
其中,Eupt、Edownt分别为抽水蓄能电站的上、下水库等值电量;Eupmax、Eupmin、Edownmax、Edownmin分别为抽水蓄能电站的上、下水库等值电量上、下限;Ωmax为抽水蓄能电站每天首末时段等值电量变化上限值;Eup0、Eup24分别为抽水蓄能电站上水库水位在每日首、末时段等效电量值。式(19)、(20)分别为抽蓄电站上、下水库库容约束;式(21)为上水库日调节量约束,限制上水库库容每日调节不超过一定数值,保证抽蓄电站能够持续正常使用。抽蓄电站状态及转换约束参考文献[18],保证每台抽蓄机组抽水蓄能和放水发电状态之间至少相隔一个时段;电站中发电机与抽水电动机启停次数均小于设定值。
g.网络安全约束。
同时考虑正常状态和N-1事故下电网的安全性,基于直流潮流,对于任意线路l,电网正常状态下的安全约束为:

其中,Pl、Plmax分别为支路l上传输功率和最大传输功率。N-1事故下的安全约束为:
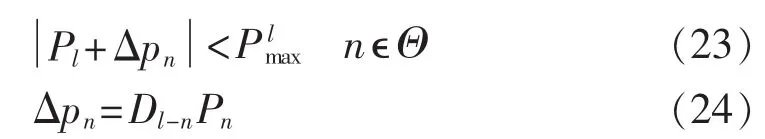
其中,Θ为N-1事故集;n为事故元件;Dl-n为功率转移因子。
h.考虑场景的约束。
随机场景s中机组备用及IL的调用需要满足功率平衡、机组出力、机组爬坡和系统安全各项约束。具体表达式与预测场景中相似,此处不再赘述。
i.弃风量小于风电自然出力的10%,意外失负荷量小于总负荷的1%。
3 基于场景的联合调度决策成本评估体系
由于目前负荷预测技术发展较为成熟,预测误差较小,本文在生成场景过程中忽略负荷随机波动分量,仅考虑风电出力的不确定性。假设随机场景的风电功率服从基于预测功率的正态分布,场景集的产生参考文献[19]。
为了正确评估每种调度决策信息下的系统综合运行成本,建立了如图2所示的基于预测和随机场景的调度决策成本评估体系,与优化算法结合,得到最佳调度运行策略,体系主要分为两大部分。
a.第一部分:基于预测场景与调度策略评估预测场景下的调度成本V1。
b.第二部分:获得调度计划后,结合场景信息形成运行环境集合,求取场景下的各类调用信息得到综合调用成本V2。
综合V1与V2,最终获取该决策状态下系统总运行成本V(V=V1+V2)。可以看出,该评估体系能够将场景下的实际调用情况有效地纳入决策优化中,达到预测与随机场景间调度决策相互影响的效果,相对于简单考虑备用需求的模型更为精确和实用。

图2 联合调度成本评估体系Fig.2 Assessment system of joint dispatch cost
4 算例分析
4.1 基础数据
本文基于MATALB/Simulink 2013a软件编写遗传算法并在10机系统上对所提模型进行求解,该系统包括10台火电机组、1个风电场、1个抽水蓄能电站、5个TL、1个IL,相关参数如表1—6所示。
4.2 对比分析
结合模型特点,设计如下4种不同调度策略。
a.策略1:风电全额上网,仅考虑火电机组参与调度,调度模型同第2节所述,但需要忽略与火电机组无关的变量。
b.策略2:在策略1的基础上,考虑抽蓄电站参与,修改调度模型,加入抽蓄相关变量和约束。
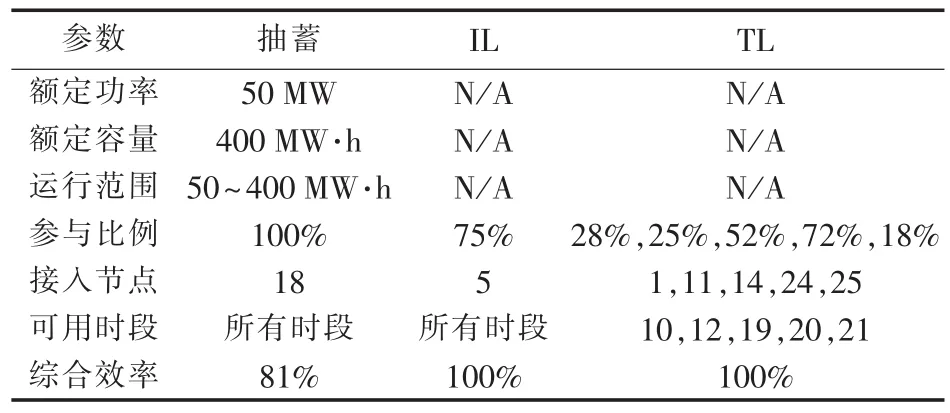
表1 抽蓄-需求响应基本参数Table 1 Basic parameters of pumped storage and demand response
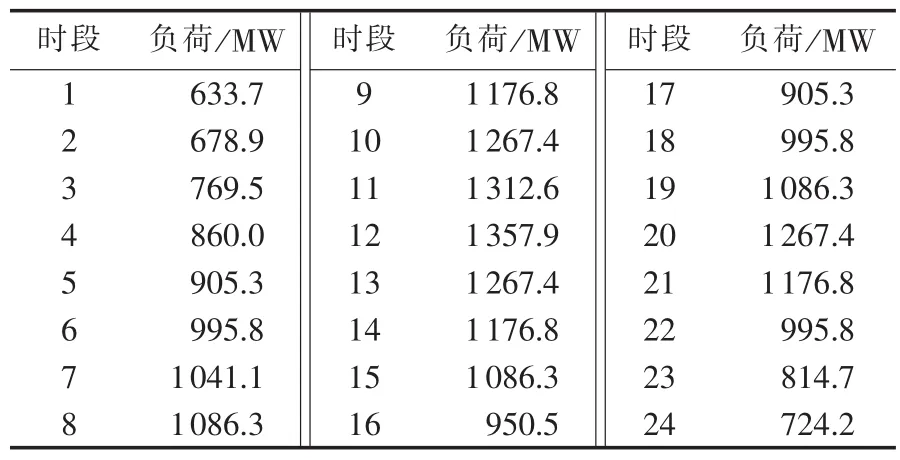
表2 负荷数据Table 2 Data of load
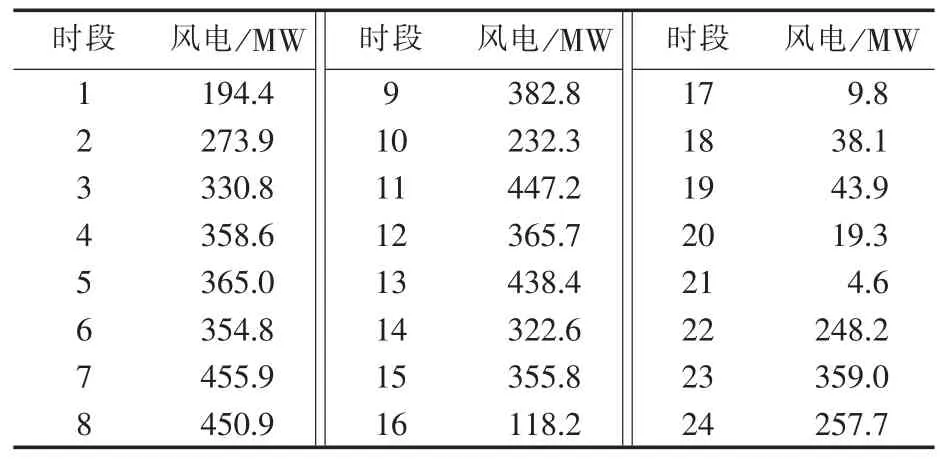
表3 风电预测数据Table 3 Data of predicted wind power
c.策略3:在策略1的基础上,考虑DR参与,修改调度模型,加入DR相关变量和约束。
d.策略4:考虑采用抽蓄与DR均参与的联合调度模式,模型如第3节所述。
分别采用4种不同运行策略时,电网调度各项主要成本、净负荷如表7、图3所示。
表7中“*”表示4种策略中该类成本的最大值。从表7和图3中可以看出,相对于策略1,策略2、3通过单独引入抽蓄或DR对负荷曲线进行优化,有效降低了峰谷之间的差距,使得火电机组出力更加>通过单独引入抽蓄或DR对负荷曲线进行优化,有效降低了峰谷之间的差距,使得火电机组出力更加平稳。其带来的直接效益是相对于策略1,策略2、3减小了约3%的机组燃料消耗,策略2降低了40%的机组启停成本。同时,由于高峰时段负荷降低,策略2、3下的备用需求也得到了有效缓解。策略4通过利用DR与抽蓄两者各自优势,进一步降低了机组燃料和启停成本,并显著降低因意外失负荷和弃风带来的损失。
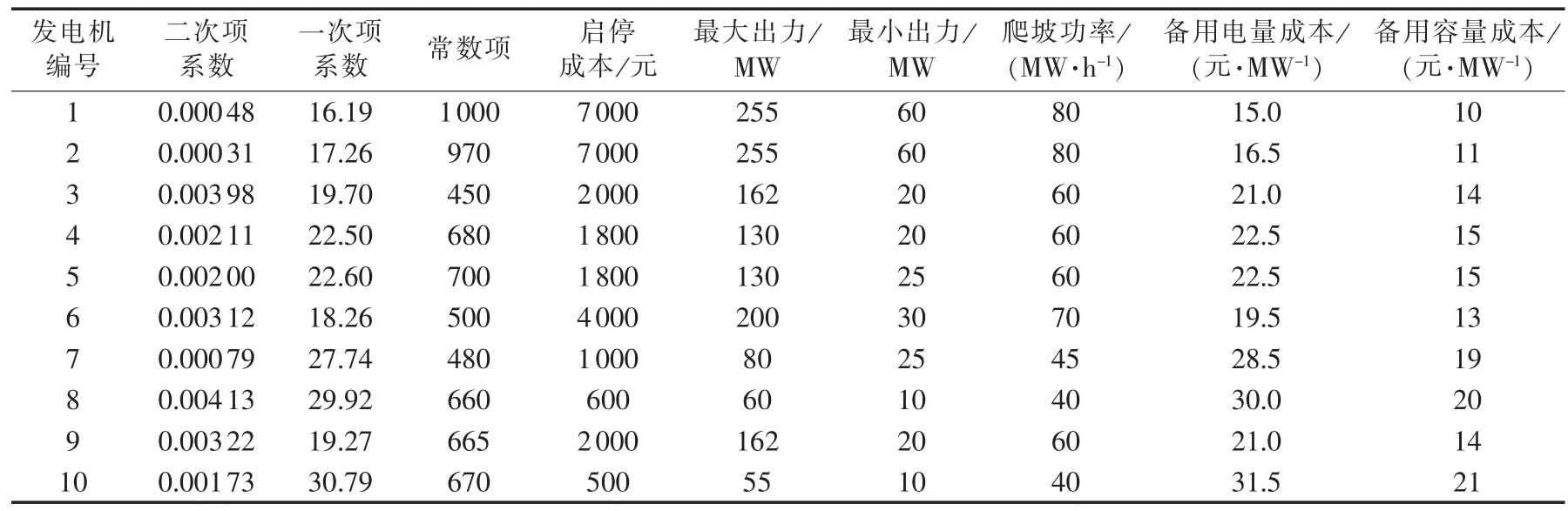
表4 发电机数据Table 4 Data of generators
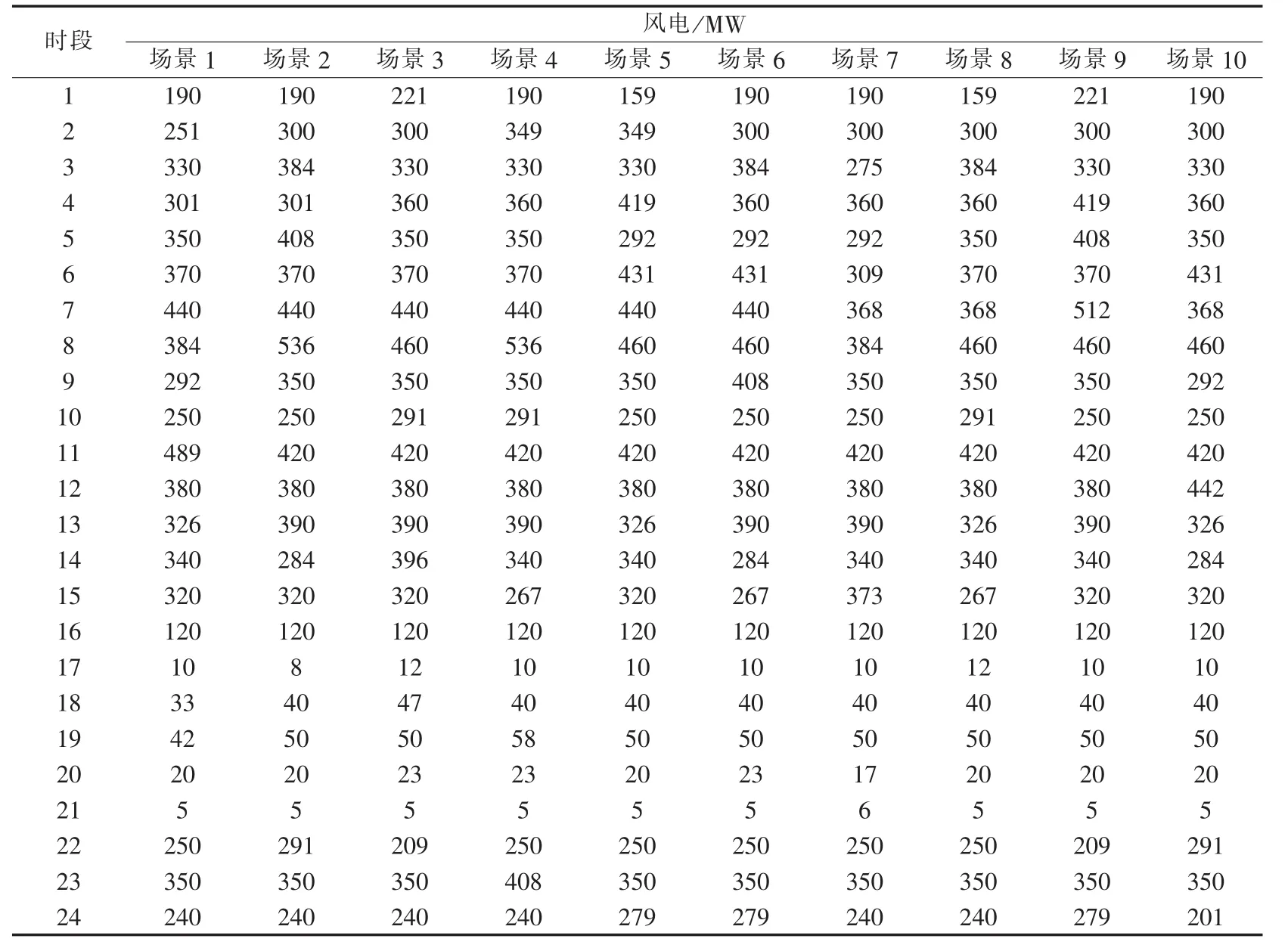
表5 风电场景集数据Table 5 Data of wind power scenario set

表6 各发电机组出力Table 6 Output power of different generators
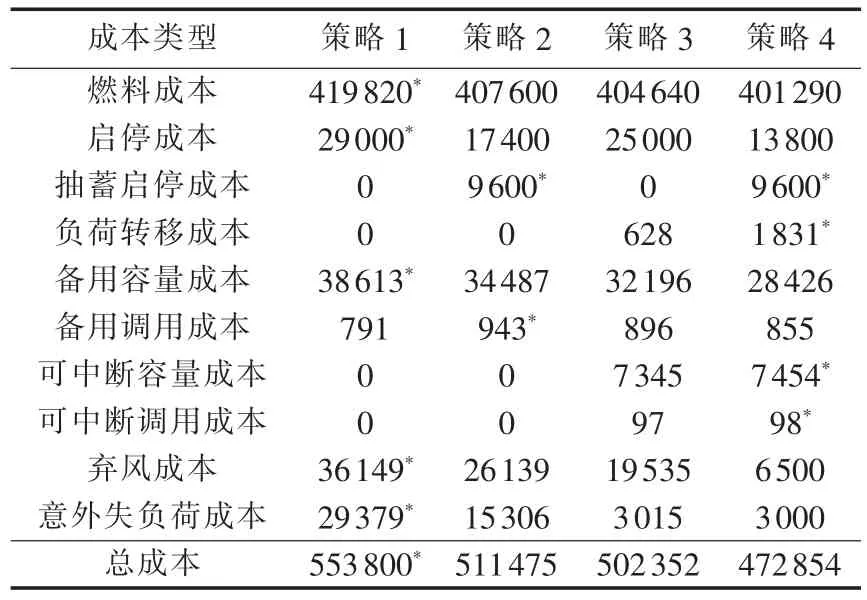
表7 4种策略下主要调度成本Table 7 Main dispatch costs for four strategies 元
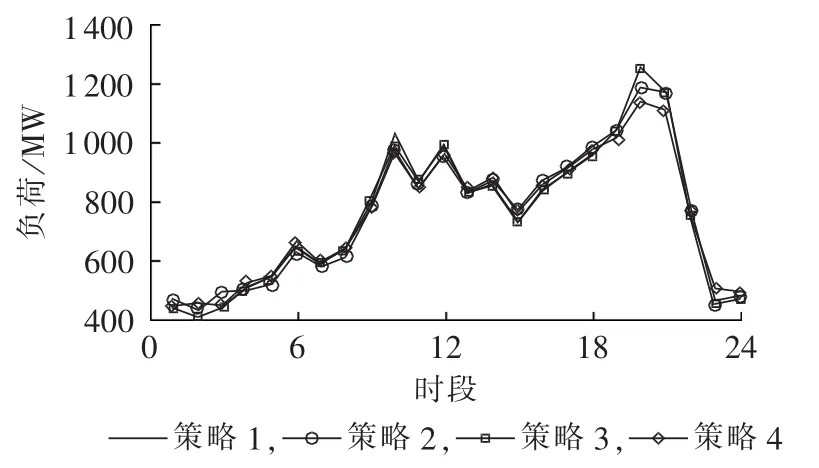
图3 4种策略下各时段净负荷情况Fig.3 Hourly net load for four strategies
表7和图3同时说明:抽蓄与DR结合,具有降低系统运行成本和提高风电接纳水平的优点。
表8为4种策略下的综合弃风和意外失负荷情况,各种策略下的值均为考虑场景概率后的加权平均值。相对于策略1,策略2、3弃风降低了约30%,其中,策略3失负荷降低了近90%。策略4通过抽蓄与DR联合,充分利用二者对负荷曲线的优化作用以及IL的备用作用,较策略2、3进一步降低了弃风水平,从而进一步降低了系统运行成本,策略4下各机组出力状态如表6所示。

表8 4种策略下场景综合弃风、失负荷量Table 8 Wind curtailment and load loss for four strategies
4.3 抽蓄-DR联合运行分析
图4和图5分别为加入DR前、后的抽蓄运行状态。2种策略下抽蓄运行状态接近,但对比两图可以看出,加入DR能够进一步降低抽水蓄能机组运行点,增加了抽蓄运行裕度,为其他辅助服务预留更大的空间。
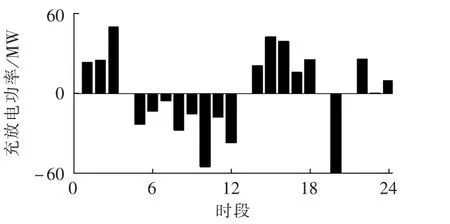
图4 策略2中抽蓄电站抽水和发电功率Fig.4 Pumping power and generating power of pumped storage power station with strategy 2
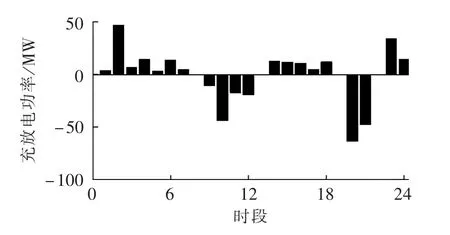
图5 策略4中抽蓄电站抽水和发电功率Fig.5 Pumping power and generating power of pumped storage power station with strategy 4
图6为策略4中DR调用状态,对比图5和图6可以发现,抽蓄和DR在本文模型下进行了有效配合,抽蓄在第 1—7、14—18、23、24 时段进行抽水蓄能,在第9—12、20、21时段进行放水发电,而 DR将第10、12、19—21时段高峰负荷分别转移到第4—8、13—18、22—24时段,充分发挥了抽水蓄能电站长时间转移能力强和DR调用灵活度高的特性,取得了削峰填谷的效果。
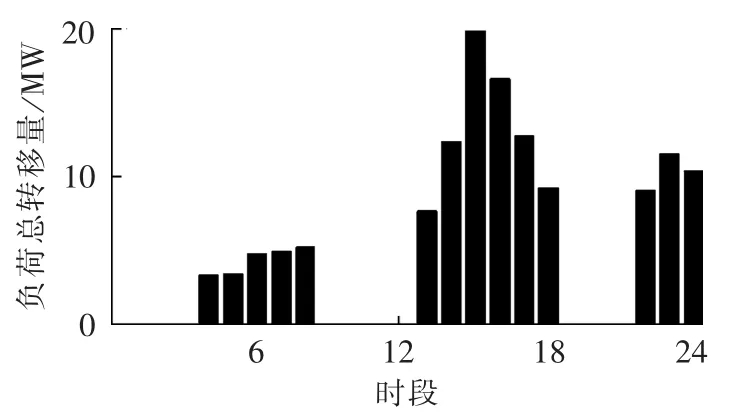
图6 策略4中负荷转移功率Fig.6 Load transfer power of strategy 4
图7为加入DR前、后抽蓄库容等效电量变化情况。策略2中抽蓄电站在24个时段中库容等效电量为 75~288 MW·h,策略 4中等效电量为 110~283 MW·h,从图中能够看出,加入DR后抽蓄整体库容更加平稳,并且在午间负荷高峰过后,保持了较好的库容水平,有效保证了后半日的运行空间,同时也延缓了随着地区负荷增长后的扩容、维护等隐性投资。
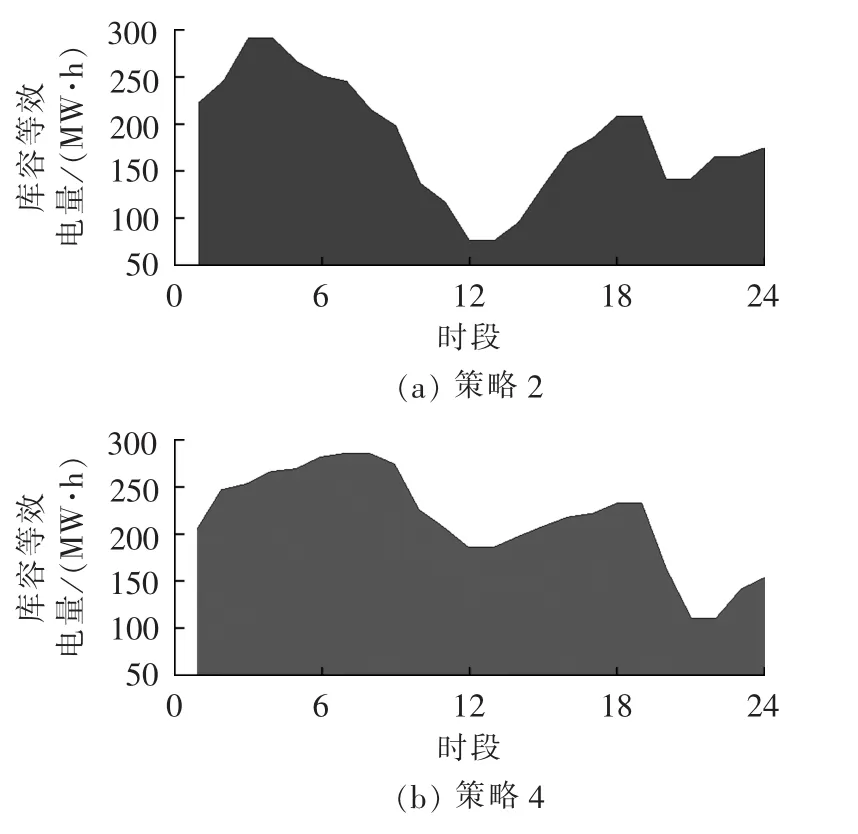
图7 需求响应加入前后抽蓄库容等效电量Fig.7 Equivalent electric power of pumped storage reservoir with and without demand response
5 结论
本文结合抽蓄和DR各自优势,建立了同时考虑抽蓄和DR参与的多场景联合安全经济调度模型;并设计基于预测和随机场景的调度决策评估体系有效地对模型进行求解,得到了最终调度结果。
结果表明,通过将抽蓄和DR引入调度模型,能够对电能进行“缓存”,并对负荷进行转移,从而调整负荷曲线,进一步减小系统净负荷峰谷差,降低系统运行、备用以及意外弃风、停电等成本,进而提高运行经济性、可靠性以及对风电的接纳能力。同时,引入IL也能有效降低系统综合备用成本。除上述显性作用外,DR还能有效缓解抽蓄运行压力,减小未来抽蓄电站投资建设的隐形成本。

