基于功率二次微分的光伏系统改进MPPT算法研究
薛云灿,李彬,王思睿,蔡昌春(.河海大学物联网工程学院,江苏常州23022;2.河海大学江苏省输配电装备技术重点实验室,江苏常州23022)
基于功率二次微分的光伏系统改进MPPT算法研究
薛云灿1,2,李彬1,王思睿1,蔡昌春1,2
(1.河海大学物联网工程学院,江苏常州213022;2.河海大学江苏省输配电装备技术重点实验室,江苏常州213022)
提出了一种基于功率二次微分的改进最大功率点跟踪(MPPT)算法(简称PQD-MPPT算法)。算法在系统启动时采用恒定占空比启动,并给出了恒定占空比的求解公式,提出了根据功率变化量来调整跟踪步长的方法,当功率变化较大时,采用自适应大步长以使系统快速跟踪到最大功率点附近,反之较小时,根据功率对占空比的二次微分值的正负进一步划分跟踪区域:即当功率二次微分值为正时,采用固定大步长以使系统快速跟踪到最大功率点附近;当功率二次微分值为负时,采用自适应小步长以使系统能够稳定工作在最大功率点处。实验结果表明,与现有变步长MPPT算法相比,该算法具有良好的跟踪性能。
光伏系统;自适应变步长;最大功率点跟踪;占空比
太阳能电池在工作时,随着日照强度、环境温度的不同,其端电压将发生变化,使输出功率也产生很大变化,故太阳能电池本身是一种极不稳定的电源。如何能在不同日照、温度的条件下输出尽可能多的电能,提高系统的效率,这就在理论和实践上提出了太阳能电池阵列的最大功率点跟踪(maximum power point tracking,MPPT)问题[1-4]。
目前,最常用的MPPT方法是扰动观察法(perturbation and observation,P&O),其算法简单,易于模块化实现,被测参数少,对传感器精度要求不高[5-9]。常规的扰动观察法由于步长的固定从而对跟踪精度和响应速度无法兼顾,变步长式扰动观察是为弥补常规扰动观察法定步长会引起响应与精度矛盾的缺陷而改良衍生出来的[10]。为解决响应与精度之间的矛盾,许多学者都对此进行了研究,其中彭会峰等在文献[7]中提出了分段自适应变步长对跟踪步长进行调整的方法,该方法同时满足了跟踪精度和响应速度的要求,跟踪速度相比于传统自适应变步长算法明显提升,但系统在启动阶段的跟踪速度并没有得到提升,当外界环境发生剧烈变化时,系统的调节时间过长,且不能稳定工作在最大功率点,算法实际控制性能并不理想。
为解决上述文献[7]中的不足,本文提出一种基于功率二次微分的改进MPPT算法(简称PQD-MPPT算法),该算法采用恒定占空比启动,并根据功率变化量来调整步长,当功率变化量较大时,设置自适应大步长以使系统快速跟踪到新的最大功率点(maximum power point,MPP)附近,反之,当功率变化量较小时,通过功率对占空比的二次微分值的正负进一步划分跟踪区域,即当功率二次微分值为正时,表示系统工作点离MPP区域较远,采用固定大步长以使系统快速跟踪到MPP附近;否则表示系统工作点离MPP较近,采用自适应小步长以使系统能够稳定工作在MPP处。
1 光伏电池特性
光伏电池无需外加电压,可以直接将太阳能转换成电能,并驱动负载工作,其工作机理是光生伏特效应,即吸收光辐射而产生电动势,光伏电池的输出特性易受外界环境如温度、光照强度等的影响。呈现典型的非线性特征,可以用下式所示的数学方程来表示光伏电池的输出电流与输出电压的关系[11]。
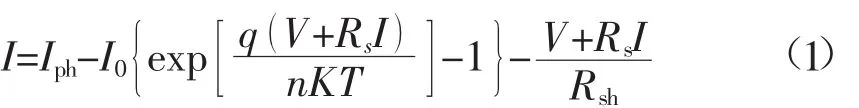
式中:I为光伏电池的输出电流,A;Iph为光生电流;I0为反向饱和漏电流;q为电子电荷量(1.69×10-19C);Rs为串联内部电阻;K为波尔兹曼常数(1.38×10-23J/K);n为光伏电池的理想因素;T为光伏电池板表面温度,K;Rsh为并联内部电阻。光伏电池的I-U和P-U特性曲线如图1所示。

图1 光伏电池的I-U和P-U特性曲线Fig.1I-U and P-U characteristic curves of PV
2 光伏阵列MPPT原理
当光伏电池处于高效的输出状态时,光伏电池与负载满足完全匹配或者直接耦合的关系,但在日常生活中很难满足光伏电池与负载的完全匹配条件,因此,为了使系统在任意光照强度和环境温度下都能工作在最大功率点附近,可通过实时变更系统的负载特性来实现最大功率点跟踪[12-16]。
通常情况下最大功率点跟踪是由DC/DC变换电路来完成阻抗匹配工作,Boost电路作为系统的DC/ DC变换电路。在忽略电路自身电阻并且变换电路的效率为100%等理想状态下,Boost电路对负载阻抗的变换关系式为[17]:

式中:R′为Boost电路等效输入阻抗;RL为负载阻抗;D为开关占空比。由上式可知,当改变Boost电路的占空比D,即可调节电路的阻抗,使其与光伏阵列输出阻抗相匹配,光伏阵列就可以输出最大功率。
3 基于功率占空比微分的MPPT算法
自适应变步长MPPT算法控制原理为:当系统工作点远离MPP区域时,采用较大跟踪步长以获得较快的动态响应特性;当系统工作点逼近MPP区域时,逐步减小跟踪步长以获得较好的稳态特性[18]。根据以上控制原理,文献[7]采用分段自适应变步长实现MPPT,其算法基于P-D微分曲线控制,利用功率微分绝对值的极值点划分区域,跟踪步长采用如下公式确定:

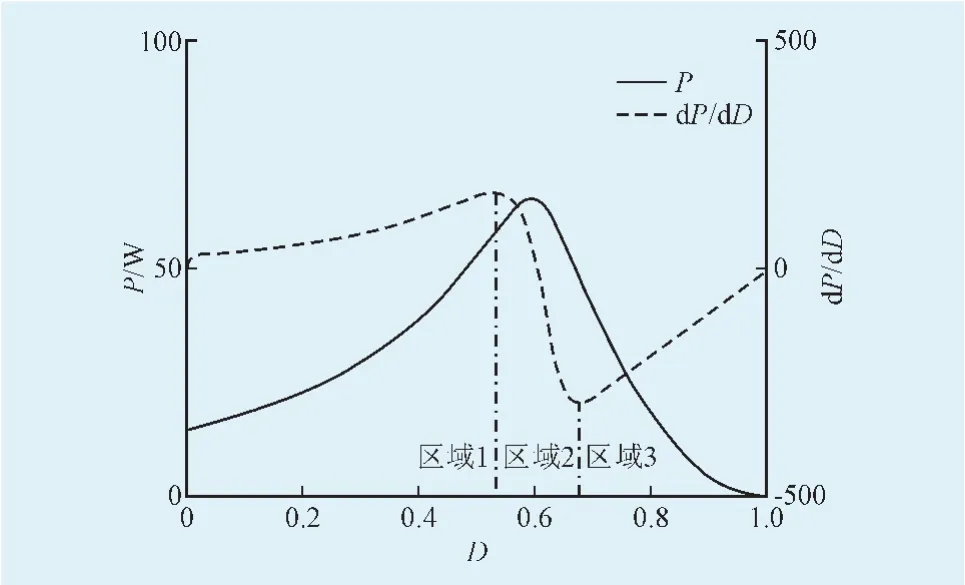
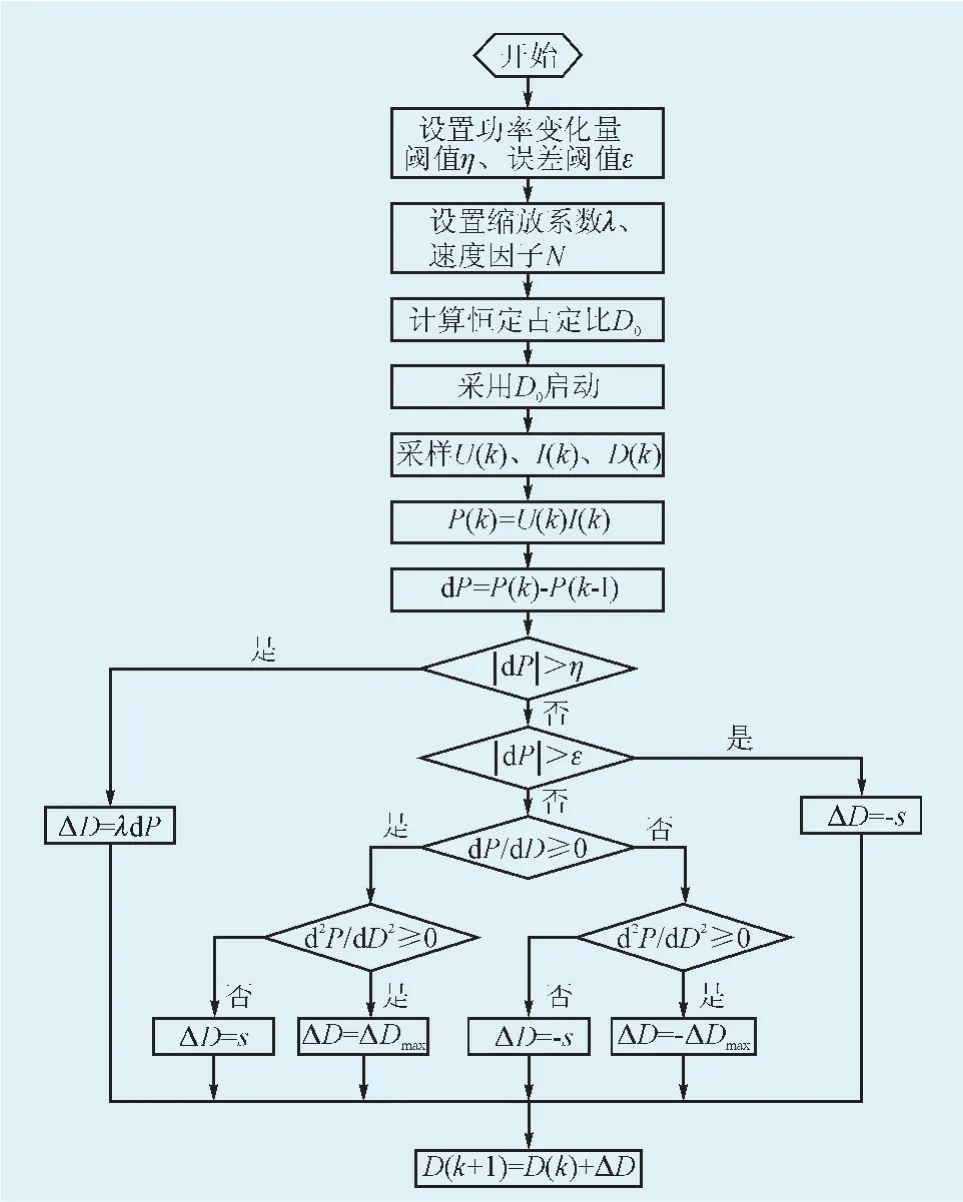
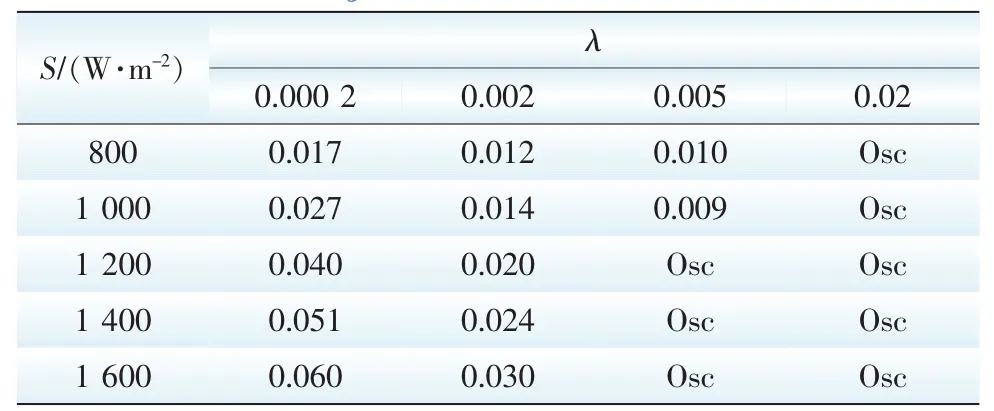
式中:N为速度因子(0 4.1光伏系统的功率占空比微分特性曲线分析由图2可知P-D微分曲线有如下特点: 图2 光伏系统P-D与dP/dD-D特性曲线Fig.2P-D and dP/dD-D characteristic curves of PV system 4.2PQD-MPPT算法 4.2.1PQD-MPPT算法中恒占空比启动控制方法 从图2可以看出,当系统工作在最大功率点时,对应的最优占空比约为0.6,基于恒电压跟踪法思想,本文提出一种恒定占空比启动控制方法,该控制方法的基本原理为:当系统工作在最大功率点时,满足如下关系式: 式中:RL为负载阻抗,为可测量;Dm为最大功率点所对应的最优占空比;Um为最大功率点电压;Im为最大功率点电流。在实际应用中,太阳电池板生产厂家通常会提供产品在标准测试条件下(S=1 000 W/m2,T=298 K)测出的Um和Im的值。由上式可知,Dm可表示为: 根据开路电压比例系数法和短路电流比例系数法可知,Um=k1Uoc,Im=k2Isc,其中k1为开路电压系数比,k1<1,一般在0.7左右;Uoc为开路电压;k2为短路电流系数比,k2<1,不同的光伏阵列k2的取值不同;Isc为短路电流[19]。由以上条件可知恒定占空比启动控制方法中恒定占空比D0可以表示为: 为验证该控制方法的有效性,通过实验采集了RL=30 Ω时单晶硅光伏电池在不同光照和温度条件下的最大功率点所对应的最优占空比,如表1所示。实验所用的单晶硅光伏电池在标准测试条件下的峰值工作电流为3.61 A,峰值工作电压为18.1 V。 表1 RL=30 Ω时的最优占空比Tab.1The best ratio cycle when RL=30 Ω 根据式(7)可求得恒定占空比D0的值约为0.60,而当外界环境发生剧烈变化时,从表1可以看出,最优占空比的波动范围也比较小,均在0.60附近,故采用恒定占空比启动,能使系统在起始阶段迅速跟踪到MPP附近,系统动态响应速度大大提高。 4.2.2PQD-MPPT算法跟踪步长调整策略 在自适应变步长方法中,不同的跟踪步长会对跟踪效果产生很大影响,文献[7]在最大功率点附近采用的自适应步长为但功率P(k)为实时采样的数据,即dP的值恒不为0,导致系统跟踪到MPP时只能在其附近来回振荡,不能稳定工作在MPP处,且当外界环境发生剧烈变化时,由于dP较大,算法所采用的跟踪步长不能迅速跟踪到新的MPP。 当外界环境条件发生剧烈变化时,为解决其所引起的跟踪时间过长问题,本算法根据功率变化量选取步长,当时,采用自适应大步长λdP进行跟踪,其中,η为功率变化量阈值;λ为缩放系数。外界环境变化越大,dP值越大,跟踪步长越大,保证了系统能迅速跟踪到新的MPP附近;反之,则根据的正负进一步划分跟踪区域: 4.2.3PQD-MPPT算法及其流程图 根据以上讨论,可概括基于功率二次微分的改进MPPT算法如下。 步骤1:设置功率变化量阈值η、误差阈值ε、缩放系数λ、速度因子N的值; 步骤2:计算恒定占空比D0,并在初始阶段采用D0启动; 步骤3:采样k时刻电压、电流和占空比的值U(k)、I(k)、D(k); 步骤4:计算功率P(k)及其变化量dP; 步骤8:D(k+1)=D(k)+ΔD; 步骤9:转步骤3。 算法流程图如图3所示。 图3 PQD-MPPT算法的流程图Fig.3Flow chart of PQD-MPPT algorithm 5.1仿真模型 根据光伏阵列的数学模型,在Matlab建立太阳能电池模型。太阳能电池在标准测试条件下(S= 1 000 W/m2,T=298 K)参数如下:最大功率65.3 W,峰值工作电流3.61 A,峰值工作电压18.1 V,短路电流3.94 A,开路电压21.2 V。 通过Matlab/Simulink搭建光伏发电系统的控制电路,如图4所示,其中光伏电池模型、Boost电路模型采用嵌入函数的形式,MPPT控制的算法用M文件编写的S函数实现,S函数模块的输入为k时刻的功率和占空比,输出为k+1时刻的占空比。 图4 仿真控制模型Fig.4Simulation control model 5.2仿真结果与分析 当外界环境发生剧烈变化时,功率变化量阈值η和缩放系数λ是决定系统调整效果的关键参数。η值取过小,会导致自适应大步长与固定步长重合;若取值过大,则算法中自适应大步长只局限于功率变化量偏大时的情况。本文中η值取外界光照强度变化50 W/m2时光伏电池输出功率的变化值,该值约为4。表2列出了当λ取值不同时,不同光照强度S的变化值所对应的系统的平均调整时间,实验初始(最终)光照强度S0为600 W/m2,表中S的单位为W/m2。 表2 不同λ值下S变化对调整时间的影响Tab.2The adjustment time of different λ and S 表2中,“Osc”指发生了振荡,从表中可以看出,当S不变时,随着λ值增大,调整时间变小,但λ值过大,会导致振荡的发生。当λ取0.002时,既能保证跟踪速度,也能避免振荡。通过改变初始光照强度的实验,其结果也表明当λ取0.002时有比较好的跟踪效果。 当系统工作点逼近MPP时,固定步长ΔDmax和自适应步长决定系统的跟踪精度和跟踪速度,若步长取值偏大,则跟踪速度快,但精度不高;反之,若步长取值偏小,则跟踪精度高,但跟踪速度较慢,实验表明,当ΔDmax=0.001,N值取2×10-5时跟踪效果较佳。 为了验证所提出改进算法的有效性,对改进算法的功率输出和占空比变化结果与原算法进行了仿真对比研究,仿真实验在Matlab2009a/Simulink进行,硬件环境为Inte(lR)Core(TM)i5,CPU 2.3 GHz,4.00 GB的内存。实验中,初始条件为标准光照强度S=800 W/m2,环境温度为T=298 K,负载阻值R= 30 Ω,误差阈值ε=0.015,仿真步长为0.005 s,运行时间为1 s,模拟日照强度在第0.3 s时从800 W/m2突然增加到1 400 W/m2。在0.6 s时又由1 400 W/m2降到1 000 W/m2。 图5(a)为基于功率占空比微分的MPPT算法仿真结果,图5(b)为PQD-MPPT算法仿真结果图。从图中可以看出,两种算法分区效果明显,当外界环境发生变化时均都能迅速跟踪到MPP,但对比两图可以发现,图5(a)中,初始阶段采用固定步长进行跟踪,经过约0.08 s跟踪到MPP,图5(b)中,在初始阶段采用恒定占空比启动,经过0.02 s就跟踪到MPP,可见采用恒定占空比启动能使系统在初始阶段迅速跟踪到最大功率点。 图5 PQD-MPPT算法和基于功率微分MPPT算法的仿真结果Fig.5Simulative results of PQD-MPPT algorithm and MPPT algorithm based on duty cycle 比较两图还可以发现,当外界环境发生剧烈变化时,图5(a)中算法跟踪到新的MPP速度较慢,调整时间较长,尤其是当光照强度突然下降时,约经过0.07 s跟踪到新的MPP,且在MPP附近发生了功率振荡的现象,图5(b)改进算法中,当外界环境发生剧烈变化时,能迅速跟踪到新的MPP,且当光照强度降低时,只要经过0.02 s就跟踪到新的MPP,没有发生功率振荡。因为在5(b)中,当算法判定外界环境发生剧烈变化时,首先采用自适应大步长使系统迅速跟踪到新的MPP附近,再通过功率二次微分值的正负判断选取相应的步长最后使系统稳定工作在MPP处,而5(a)中直接通过功率二次微分的正负选取固定步长或者自适应小步长,而固定步长本身比较小,使得跟踪速度较慢,调整时间太长。 可见,改进算法通过引入恒定占空比及自适应大步长使得系统在动态响应特性以及稳态特性较原算法都有了较大的改善。 本文针对基于功率占空比微分MPPT算法的不足做出了改进,提出了基于功率二次微分的改进MPPT算法,该算法直接将占空比作为控制变量,采用恒定占空比启动使系统具有很快的动态响应速度,对常规的自适应步长方法进行了改进,建立了所提出算法的仿真模型并对基于功率占空比微分MPPT算法和改进算法进行了仿真比较。理论和仿真实验表明,该改进算法能在系统初始阶段迅速跟踪到最大功率点,且能迅速感知外界环境变化并能稳定工作在MPP处,实现了MPPT精确性和快速性的兼备,有效地提高了光伏系统的发电效率。 [1]黄舒予,牟龙华,石林,等.自适应变步长MPPT算法[J].电力系统及其自动化学报,2011,23(5):26-30.HUANG Shuyu,MU Longhua,SHI Lin,et al.Adaptive variable step size MPPT algorithm[J].Proceedings of the CSU-EPSA,2011,23(5):26-30(in Chinese). [2]刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6):91-94.LIU Bangyin,DUAN Shanxu,LIU Fei,et al.Photovoltaic array maximum power point tracking based on improved perturbation and observation method[J].Transactions of China Electrotechnical Society,2009,24(6):91-94(in Chinese). [3]刘观起,游晓科,杨玉新,等.光伏发电系统最大功率点跟踪方法研究综述[J].陕西电力,2012,40(2):18-22.LIU Guanqi,YOU Xiaoke,YANG Yuxin,et al.Study on maximum power point tracking techniques for photovoltaic power generation system[J].Shaanxi Electric Power,2012,40(2):18-22(in Chinese). [4]栗秋华,周林,刘镪,等.光伏并网发电系统最大功率跟踪新算法及其仿真[J].电力自动化设备,2008,28(7):21-25.LI Qiuhua,ZHOU Lin,LIU Qiang,et al.Simulative research of MPPT for photovoltaic power system[J].Electric Power Automation Equipment,2008,28(7):21-25(in Chinese). [5]李俊良,王新涛,史吏,等.恒定电压法与变步长滞环比较法结合的MPPT算法研究[J].陕西电力,2013,41(7):55-58,64.LI Junliang,WANG Xintao,SHI Li,et al.Study on MPPT algorithm combined CVT and hysteresis comparing method of variable step size[J].Shaanxi Electric Power,2013,41(7):55-58,64(in Chinese). [6]温嘉斌,刘密富.光伏系统最大功率点追踪方法的改进[J].电力自动化设备,2009,29(6):81-84.WEN Jiabin,LIU Mifu.Improvement of maximum power point tracking for photovoltaic system[J].Electric Power Automation Equipment,2009,29(6):81-84(in Chinese). [7]彭会锋,孙建平,曹相春,等.基于功率占空比微分曲线的光伏系统MPPT算法[J].电力自动化设备,2013,33(6):124-127.PENG Huifeng,SUN Jianping,CAO Xiangchun,et al.MPPT algorithm based on power duty cycle differential characteristic curve for photovoltaic system[J].Electric Power Automation Equipment,2013,33(6):124-127(in Chinese). [8]赵春江,杨金焕,陈中华,等.太阳能光伏发电应用的现状及发展[J].节能技术,2007,25(5):461-465.ZHAO Chunjiang,YANG Jinhuan,CHEN Zhonghua,et al.State&development of photovoltaic application[J].Energy Conservation Technology,2007,25(5):461-465(in Chinese). [9]周倩,薛建,于辰,等.基于Matlab的光伏并网系统的仿真分析[J].陕西电力,2012,40(3):19-22.ZHOU Qian,XUE Jian,YU Chen,et al.Analysis and simulation for grid-connected photovoltaic system based on matlab[J].Shaanxi Electric Power,2012,40(3):19-22(in Chinese). [10]朱晓亮,程晓舫,张忠政,等.太阳电池最大功率及其跟踪模式[J].节能技术,2012,30(4):361-365.ZHU Xiaoliang,CHENG Xiaofang,ZHANG Zhongzheng,et al.The maximum power and tracking mode of solar cell[J].Energy Conservation Technology,2012,30(4):361-365(in Chinese). [11]陈亚爱,周京华,李津,等.梯度式变步长MPPT算法在光伏系统中的应用[J].中国电机工程学报,2014(19):3156-3161.CHEN Yaai,ZHOU Jinghua,LI Jin,et al.Application of gradient variable step size MPPT algorithm in photovoltaic system[J].Proceedings of the CSEE,2014(19):3156-3161(in Chinese). [12]曹冲,卢永杰,佘小莉,等.基于改进扰动法的光伏电池最大功率点跟踪研究[J].陕西电力,2011,39(12):62-67.CAO Chong,LU Yongjie,SHE Xiaoli,et al.Probe intophotovoltaic cell maximum power point tracking based on improved perturbation method[J].Shaanxi Electric Power,2011,39(12):62-67(in Chinese). [13]孙佳,林永君,王甜甜,等.光伏系统最大功率点跟踪算法的仿真研究[J].陕西电力,2013,41(9):29-32.SUN Jia,LIN Yongjun,WANG Tiantian,et al.Probe into simulation of maximum power point tracking algorithms for photovoltaic system[J].Shaanxi Electric Power,2013,41(9):29-32(in Chinese). [14]袁银梅.太阳能电池最大功率跟踪的线性近似法分析[J].节能技术,2011,29(3):230-232,284.YUAN Yinmei.Experimental analysis of solar cell maximum power point tracking based on linear approximation method[J].Energy Conservation Technology,2011,29(3):230-232,284(in Chinese). [15]LIU Fangrui,DUAN Shanxu,LIU fei.A variable step size INC MPPT method for PV systems[J].IEEE Transactions on Industrial Electronics,2008,55(7):2622-2628. [16]车本佳,冯毅.太阳能最大功率跟踪装置的设计[J].节能技术,2011,29(6):552-555,559.CHE Benjia,FENG Yi.Design of a new type of solar MPPT system[J].Energy Conservation Technology,2011,29(6):552-555,559(in Chinese). [17]蔺娜,刘星,葛晨,等.基于S-函数改进电导法的光伏阵列最大功率点的跟踪[J].西北水电,2014(2):90-92,99.LIN Na,LIU Xing,GE Chen,et al.Tracking of maximum power point of photovoltaic array by incremental conductance method improved on base of s-function[J].Northwest Water Power,2014(2):90-92,99(in Chinese). [18]乔兴宏,吴必军,王坤林,等.基于模糊控制的光伏发电系统MPPT[J].可再生能源,2008,26(5):13-16.QIAO Xinghong,WU Bijun,WANG Kunlin,et al.MPPT by using fuzzy control combined with PID for photovoltaic energy generation system[J].Renewable Energy Resources,2008,26(5):13-16(in Chinese). [19]张天时,王国华,矫振伟,等.基于PSoC的太阳能MPPT系统控制器设计[J].节能技术,2013,31(2):175-179.ZHANG Tianshi,WANG Guohua,JIAO Zhenwei,et al.Solar energy MPPT system based on PSoC controller design[J].Energy Conservation Technology,2013,31(2):175-179(in Chinese). (编辑徐花荣) An Improved MPPT Algorithm Based on Power Quadratic Differential for Photovoltaic System XUE Yuncan1,2,LI Bin1,WANG Sirui1,CAI Changchun1,2 An improved maximum power point tracking(MPPT)algorithm based on power quadratic differential(in brief,PQD-MPPT algorithm)is proposed in this paper.The constant duty cycle method is adopted in its initial stage in the improved algorithm and the solving formula of the constant duty cycle is put forward.The adjustment method of the step according to the variation of power is also presented.When the power changes greatly,an adaptive large step is adopted to make the system to track near the maximum power point quickly. Otherwise,the tracking areas are divided into two parts according to whether the power quadratic differential is positive or negative.When the power quadratic differential is positive,a fixed large step is adopted to make the system to track near the maximum power point quickly.Otherwise,an adaptive small step is adopted to make the system to work stably at the maximum power point.The experimental results show that by comparison with the existing variable step MPPT algorithm,the improved algorithm has better tracking performance. photovoltaic system;adaptive variable stepsize;MPPT;duty cycle 1674-3814(2015)06-0117-07 TM615 A 2014-12-16。 薛云灿(1965—),男,博士,教授,主要研究方向为先进控制理论与应用; 李彬(1989—),男,硕士研究生,主要研究方向为光伏发电建模与优化; 王思睿(1991—),女,硕士研究生,主要研究方向为光伏发电建模与优化; 蔡昌春(1981—),男,博士,讲师,主要研究方向为电力系统建模。4 基于功率二次微分的改进MPPT算法



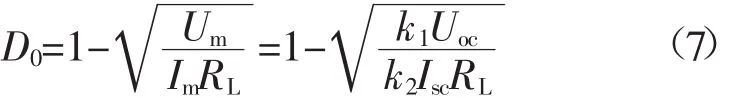

5 仿真实验

6 结语
(1.College of IOT Engineering,Hohai University,Changzhou 213022,Jiangsu,China;2.Key Laboratory of Power Transmission and Distribution Equipment Technology,Hohai University,Changzhou 213022,Jiangsu,China)

