联合循环机组维护成本建模及求解

张彦涛，苏峰，汪洋，徐帆，丁恰，涂孟夫（．国电南瑞科技股份有限公司，江苏南京006；．国家电网公司华北分部，北京00053）

联合循环机组维护成本建模及求解

张彦涛1，苏峰2，汪洋2，徐帆1，丁恰1，涂孟夫1
（1．国电南瑞科技股份有限公司，江苏南京210061；2．国家电网公司华北分部，北京100053）

为更加准确合理计算联合循环机组发电成本，在传统联合循环机组组合模型基础上，引入联合循环机组维护成本模型，该模型的难点是启机维护成本和运行维护成本在同一计算周期内的互斥关系。针对这一难点，首先将启机维护成本叠加到模式转移成本中考虑，然后通过分析联合循环机组中燃气轮机在计算周期内是否有启机，确定目标发电成本是否考虑运行维护成本，同时使用线性化技巧等价变换非线性表达为线性表达，建立MIP模型。利用系统实际运行数据对文中模型进行测试，测试表明该模型有效解决联合循环机组维护成本问题，优化结果合理。

联合循环机组；混合整数线性规划；启机维护成本；运行维护成本；模式转移

近年来，在全球常规能源逐步走向枯竭，环保呼声日渐高涨的背景下，我国作为世界上能耗最高的国家之一，伴随国内智能电网建设的加强，迫切需要可再生能源发电技术快速发展，一些利用效率高，响应速度快，环境友好的发电机组在电力系统中的比重也越来越大。例如（combined cycle gas turbine，CCGT）燃气蒸汽联合循环热电联供机组具有热效率高、污染排放低、节省投资、建设周期短、启停快捷、调峰性能好、占地少、节水、厂用电率低和可靠性强、维修方便等优点，联合循环机组装机容量在逐步提高，逐步成为我国电力工业的一个重要组成部分。

CCGT运行特性不同于一般火电机组，其是多种模式运行方式及不同模式间的转移限制和转移成本，使得联合循环机组优化编制模型变得极其复杂。针对此问题，已存在多种解决方案，文献[1]利用拉格朗日和库恩塔克方法在假定CCGT组件运行状态已定情况下进行优化。文献[2]在CCGT不同模式对应不同曲线模型的假设前提下利用动态规划算法求解。文献[3-4]利用动态规划和拉格朗日松弛法分UC和ED两步分开优化，解决联合循环机组模式转移问题。与此同时，整数规划[5-9]理论基础不断完善，文献[5]建立MIP模型，通过对比分析拉格朗日松弛算法和对偶单纯型算法，展示MIP模型在实际运用中的优越性。另外，引入分支定界和多种切平面方法后，使得MIP模型的可求解规模得到很大扩展，MIP模型逐步成为实际应用中的主流优化模型，并同步推动基于CCGT机组的MIP模型[10-15]发展，不断完善CCGT机组模型的同时，展现了MIP模型实际应用中的优越性能。文献[15]通过引入模式转移矩阵建立MIP模型，更加简洁直观地描述了模式转移特性，同时解决了模式转移成本问题，并在实际中得到很好的应用。

本文在上述文献的基础上，引入了CCGT维护成本问题，针对燃气轮机和蒸汽轮机维护成本的不同计算方法，以及燃气轮机2种维护成本在同一优化周期内不能并存的先决条件，利用数学线性化技巧进行等价变化，建立了考虑CCGT机组维护成本的MIP模型。

1维护成本介绍

CCGT机组一般由若干台燃气轮机（CT）、余热锅炉（HRSG）和蒸汽轮机（ST）组成[3，15]，图1为由2CT-1ST构成的CCGT的结构图。

图1　联合循环机组（2CT-1ST）结构Fig.1Configuration of CCGT（2CT-1ST）

CCGT机组维护成本分为运行维护成本和启机维护成本，维护成本以天为单位进行计算。组成CCGT的不同类型组件考虑维护成本的方式存在一定差异，燃气轮机CT计算周期内有且只有一种维护成本，若CT在计算周期内没有启机，且有运行，则只考虑该时间段产生运行维护成本；若计算周期内有启机，则考虑启机维护成本，不再考虑运行维护成本；2种维护成本在同一周期内只考虑一种即可。对于蒸汽轮机ST来说，由于ST是由CT产生的废气进行驱动，故而认为ST没有启机成本和发电成本，但ST有维护成本，并且可同时考虑2种维护成本，如果ST在计算周期内没有启机，且有运行，则只考虑运行维护成本；ST在计算周期内有启机，且有运行，则需同时计算2种维护成本。

2　维护成本数学模型

2.1模式转移原理分析

组成CCGT的若干台CT与ST的不同组合构成了CCGT不同的运行模式。对于由2CT-1ST（GT1、GT2和ST1）组成的CCGT，其6种运行模式包含1CT（GT1或者GT2），1CT+1ST（GT1+ST1/2或者GT2+ST1/2）和2CT+1ST（GT1+GT2+ST1），2CT（GT1+GT2）。此外，停机也作为一种特殊模式，共7种运行模式。不同的运行模式具备各自的出力范围、成本曲线、最小开停时间以及爬坡/滑坡率等。因而在模式模型中，为了精细的描述和处理各个模式，将每种模式视为一台虚拟机。同时，由于这些模式对应同一台CCGT，在同一时刻，只有一种模式处于运行状态[13-15]。

CCG运行特性使得各模式间不能任意转换[4，13，15]，这也是其与普通机组的最大区别。图2给出了CCGT的7种模式之间的转换关系。

图2　联合循环机组（2CT-1ST）的模式转移图Fig.2State transition diagram for CCGT（2CT-1ST）

需要指出的是，对于由更多台CT与ST构成的CCGT，其模式转移关系要更复杂。

2.2维护成本数学表达

CCGT的模式模型在前述文献[1-4，10，14-15]中已有详细分析和精辟阐述。本文仅针对CCGT机组的维护成本，也是建模的难点，建立自己的模型，考虑到模型完整性，将CCGT维护成本建模的依赖性约束描述如下。

2.2.1目标函数及CCGT运行特性

对于CCGT来说，其运行成本包括发电成本、模式转移成本和维护成本：

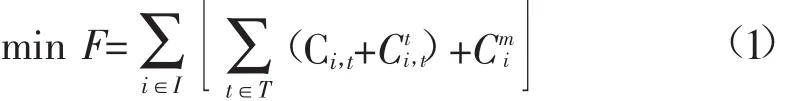
式中：I为CCGT机组集；T为调度周期时段集；Ci，t为机组i在t时的发电成本；为机组i在t时的模式转移成本；为机组i的维护成本。

对于模式模型来说，由于CCGT的各模式被虚拟化为相应的虚拟机，故各模式的出力范围约束、爬坡/滑坡约束、最小开停机时间约束以及发电成本的建模方法与普通机组类似。各模式对应的虚拟机组出力和发电成本可表达为：

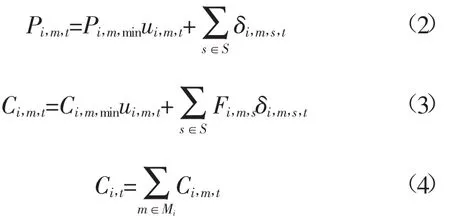
式中：Pi，m，t为CCGT机组i模式m时刻t的出力；Pi，m，min为机组i模式m的最小出力；ui，m，t为0/1量，表示机组i模式m时刻t的开停状态；S为成本曲线所分段集合；Mi为CCGT机组i的运行模式集合；δi，m，s，t为机组i模式m时刻t在成本曲线s段上的出力；Ci，m，t为机组i模式m时刻t的发电成本；Ci，m，min为机组i模式m出力下限对应的发电成本；Fi，m，s为机组i模式m在成本曲线s段上的微增成本。

CCGT在任一时刻只能处于一种模式，即对应于同一CCGT的各模式在同一时刻只能有一种处于运行状态[14-15]：

由CCGT运行特性可知，CCGT模式之间不能任意转换，通过引入模式转移矩阵，更加简洁直观地描述了模式转移特性，式（6）给出了模式转移关系表达式。

式中：Ai，m，n为机组i模式转移矩阵A中的元素，为0/1量，用以标记机组i是否可以从模式m转移至模式n，1表示可转移，0表示不可转移。

CCGT从一种模式转移到另一模式的同时，必然会伴随其组件机组CT或ST的启停，从而产生转移成本：

2.2.2维护成本特性

由于CT的启机维护成本和运行维护成本同一计算周期内互斥，因此，判定CT在计算周期内是否启机成为计算维护成本的先决条件。首先通过CCGT在各时段的运行模式推导出其组件机组的运行状态，CCGT运行模式和其组件机组的运行状态可以表述为：

式中：ri，j，t为0/1量，表示CCGT机组i中组件机组j在时刻t的开停状态；mi，m，j为0/1量，表示CCGT机组i模式m中是否包含组件机组j。

根据CCGT中各组件机组在各个时刻的开停状态，判断各组件机组在各个时刻是否有启机：

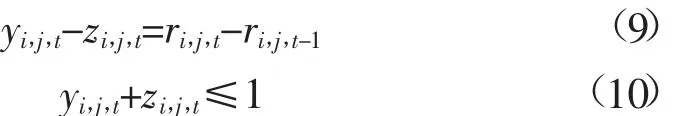
式中：yi，j，t为0/1量，表示CCGT机组i中组件机组j在时刻t是否有启机；zi，j，t为0/1量，表示CCGT机组i中组件机组j在时刻t是否有停机。

根据CCGT中各组件机组在计算周期内各个时段的启停信息，判断各组件机组在计算周期内是否有启机：

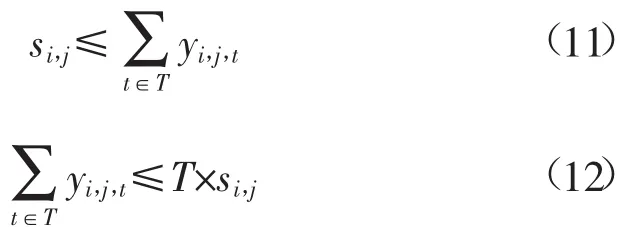
式中：si，j为0/1量，表示CCGT机组i中组件机组j在计算周期内是否有启机。

CCGT机组i中组件机组j在计算周期内的启机信息确定之后，其CCGT的维护成本表示为：

式中：Di，j为CCGT机组i中组件机组j单位时段的运行维护成本；为CCGT机组i中组件机组j运行时段产生的运行维护成本；Ei，j为CCGT机组i中组件机组j启机维护成本；I1和I0分别为由燃气轮机和蒸汽轮机组成的集合。从式（13）可以看出，CT机组运行维护成本和启机维护成本不能并存，ST机组同时考虑2种维护成本。

2.2.3维护成本模型简化处理

式（8）~（14）完整描述了CCGT维护成本的建模过程，并给出了维护成本的精准表达。经分析可知，式（13）中运行维护成本部分为非线性表达式，故而优化模型为MIQP模型，为提高优化模型的优化性能，利用线性化技巧对式（13）进行线性等价变换，转化MIQP模型为MIP模型。

模式转移的本质就是CCGT中组件机组的启停，因此，CT和ST的启停必然伴CCGT模式转移，故而，可以叠加启机维护成本至模式转移成本中，计算模式转移成本的同时也完成了启机维护成本的计算，模式转移成本约束表达式（7）转化为：

式中：Ei，m，n为CCGT机组i从模式m转移到模式n的启机维护成本，如果模式转移伴随CT机组启机，则为CT启机维护成本，如果伴随ST启机，则为ST启机维护成本，否则，意味着模式转移伴随CT或者ST停机，则Ei，m，n为零。

另外，由于蒸汽轮机同时考虑2种维护成本，故而可把蒸汽轮机运行维护成本叠加至包含该蒸汽轮机的模式成本曲线中，通过式（3）计算蒸汽轮机运行维护成本。通过以上简化处理后，式（13）简化为：

式（14）和（16）合并可得：

式（17）中，si，j和ri，j，t均为未知量，因此，维护成本为非线性表达式，引入中间变量，进行线性转化：

si，j、ri，j，t和vi，j，t均为0/1变量，由式（18），可将式（17）转化为线性表达式：

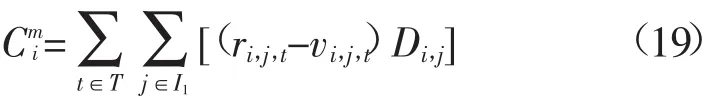
接下来利用数学技巧对等式约束（18）线性等价变换，其等价形式为：

至此，式（8）—（12）、式（15）、式（19）—（22）构成了考虑CCGT机组维护成本的MIP模型。比较式（13）和式（19），模型得以简化，计算效率和算法稳定性得到提高，提升了实用化水平。

3　算例分析

本文以某电网系统的实际数据构造算例，对建立的模型进行验证分析，计算周期为一天，15 min一个时段，共96时段。本系统供电由外购电、普通火电机组和CCGT机组提供，共包含11台建模机组，其中有一台为CCGT机组，其组成结构为2CT-1ST（GT1+ GT2+ST1）。普通火电机组全部为燃油机组，CCGT机组发电成本低于普通火电机组，外购电的晚上价格低于CCGT机组，白天价格高于CCGT机组，低于普通火电机组。外购电拟定7:00—23:00点为白天价格0.92 Mop/MW，其余时段为晚上价格0.68 Mop/MW，另外，外购电功率上限为500 MW。GT1和GT2运行维护成本为2 241 Mop/h，ST1运行维护成本已叠加到包含ST1的模式成本曲线中。

图3给出了某天系统负荷预测数据。

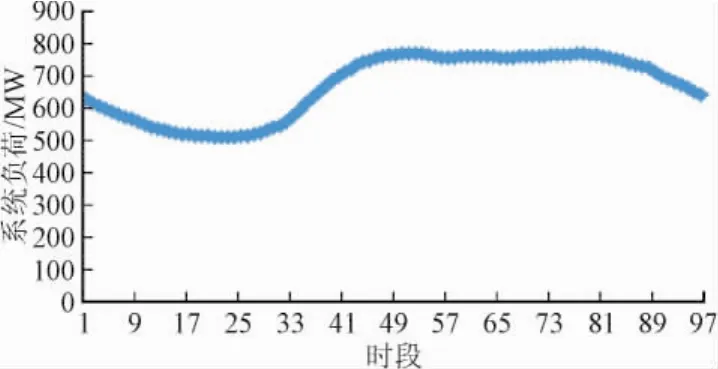
图3　短期系统负荷预测Fig.3Short-term load forecast

CCGT组件机组的启机维护成本和模式转移成本叠加，修正后的模式转移成本（单位：Mop）如表1所示。

CCGT中各组件机组初始（计算周期的前一点）出力状态如表2所示。

从表2中容易看出，CCGT机组初始运行模式为模式4。

3.1不考虑维护成本

首先不考虑维护成本优化机组出力，CCGT机组出力曲线及运行模式变化情况如图4、5所示。

表1　模式转移成本Tab.1Mode transforms cost

表2　初始出力状态Tab.2Initial power and status

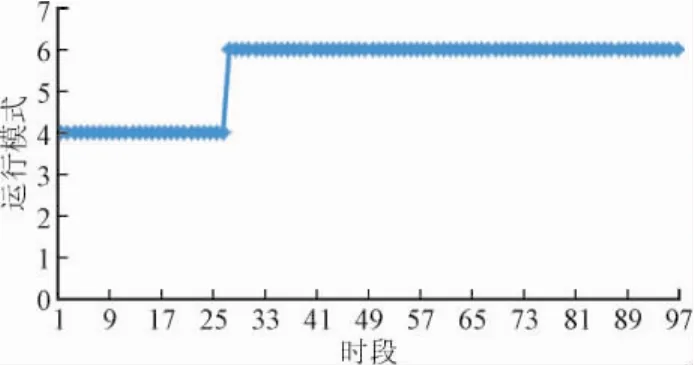
图4　CCGT运行模式Fig.4Running mode of CCGT

图5　CCGT出力曲线Fig.5Power curves of CCGT

从图4、5中可以看出，CCGT机组0—7点运行在模式4，和初始时段运行模式相同，7点钟从模式4转移到模式6运行，原因是外购电在7点钟之后为白天价格，价格高于CCGT发电，所以CCGT转移到模式6满发。然而，23点之后，外购电为晚上价格，价格低于CCGT发电，但CCGT没有从模式6转移到模式4或者模式5来降低出力，原因是此时间段内系统负荷高于650 MW，外购电上限为500 MW，系统需自己供电150 MW，又由于CCGT发电成本低于其他普通火电机组，且CCGT上限为126 MW，故CCGT仍旧运行在模式6保持满发。

3.2考虑维护成本

算例3.1中可以看出，计算周期内CCGT从模式4转移到模式6，伴随GT2启机。然而，GT1在计算周期内连续运行，没有启机。假设在上述运行方式下考虑CCGT维护成本，GT2有启机维护成本，GT1有运行维护成本。本算例将设定考虑维护成本，分析CCGT运行模式和算例3.1的差异，图6、7展示了CCGT考虑维护成本后的运行模式和出力曲线。

图6　CCGT运行模式Fig.6Running mode of CCGT

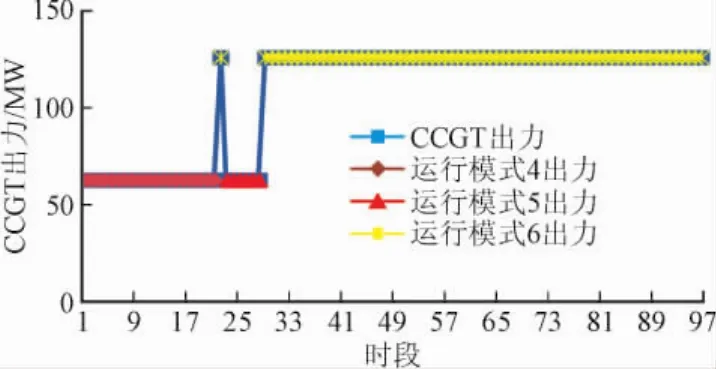
图7　CCGT出力曲线Fig.7Power curves of CCGT

从图6、7可以看出，与算例3.1对比，CCGT增加两次模式转移，首先从模式6转移到模式5，伴随GT1停机，然后从模式5转移到模式6，伴随GT1启机。2次转移的结果是，GT1在计算周期内有启机，因此，计算启机维护成本，不计算运行维护成本。GT1在计算周期内连续运行的运行维护成本为53 784 Mop，2次模式转移产生的启机维护成本和模式转移成本总加为51 492 Mop，易知，运行维护成本偏高，CCGT通过2次转移使得GT1启机，进而利用启机维护成本和模式转移成本总加替代运行维护成本。

3.3提升启机维护成本

从算例3.2中可以看出，CCGT通过2次模式转移规避运行维护成本，假设提升GT1启机维护成本，使得GT1启机维护成本叠加模式转移成本大于GT1计算周期内连续运行维护成本，CCGT运行模式又会如何变化。启机维护成本提升一个数量级之后，CCGT运行模式和出力曲线如图8、9所示。

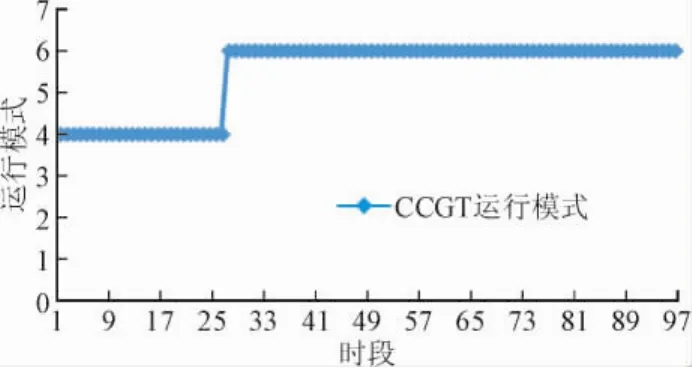
图8　CCGT运行模式Fig.8Running mode of CCGT

图9　CCGT出力曲线Fig.9Power curves of CCGT

从图8、9可以看出，CCGT运行模式和出力曲线和算例3.1相同，并没有通过2次模式转移来规避运行维护成本。原因是启机维护成本提升一个数量级之后，GT1 2次模式转移产生的启机维护成本和模式转移成本累加大于GT1运行维护成本，因此，GT1保持连续运行，取消2次模式转移。

4　结语

本文建立了关于CCGT维护成本的MIP模型，阐述了CCGT维护成本的建模过程，并利用数学线性化技巧转化维护成本的非线性表达为线性表达，给出了简化的线性表达式。该模型在考虑维护成本后，CCGT机组模式转移更加精确合理并接近于实际运行，最大限度地使得发电成本最低。同时利用某实际运行系统对其进行了详细分析与测试，证明了本文模型的正确性和有效性。本文优化模型已在某电网系统中持续稳定运行2年半之久，实际运行效果良好。

[1]RIFAAT R M.Economic dispatch of combined cycle cogenerationplantswithenvironmentalconstraints[C]// Proceedings of IEEE EMD’98 1998 International Conference，Singapore:IEEE，1998:149-153.

[2]BJELOGRLIC M R.Inclusion of combined cycle plants into optimal resource scheduling[C]//Proceedings of IEEE PES Summer Meeting，USA:IEEE，2000:189-194.

[3]LU Bo，SHAHIDEHPOUR M.Short-term scheduling of combined cycle units[J].IEEE Trans on Power Systems，2004，19（3）:1616-1625.

[4]LU Bo，SHAHIDEHPOUR M.Unit commitment with flexible generation units[J].IEEE Trans on Power Systems，2005，20（2）:1022-1034.

[5]LI Tao.A case of lagrangian relaxation versus mixed integer programming[J].IEEE Trans on Power Systems，2005，20（4）:2015-2025.

[6]NEMHAUSER G L，WOLSEY L A.Integer and combinatorial optimization[M].New York:Wiley，1998:0-763.

[7]WOLSEY L A.Integer programming[M].New York:Wiley，1998:0-288.

[8]SCHRIJVER Alexander.Theory of linear and integer programming[M].New York:Wiley，1998:0-484.

[9]PAUL WILLIAMS H.Logic and integer programming[M]. New York:Springer-Verlag，2009:0-214.

[10]CHANG G W，CHUANG G S，LU T K.A simplified combined-cycle unit model for mixed integer linear programming-based unit commitment[C]//Proceedings of IEEE PES General Meeting，USA:IEEE，2008:1-6.

[11]CROXTON K L，GENDRON B，MAGNANTI T L.A Comparison of mixed-integer programming models for non-convex piecewise linear cost minimization problems[J]. Management Science，2003，49（9）:1268-1273.

[12]丁晓莺，刘林，王锡凡，等.考虑灵活运行机组的随机机组组合模型[J].电力系统自动化，2009，33（18）:23-27. DING Xiaoying，LIU Lin，WANG Xifan，et al.Stochastic unit commitment method with flexible generating units[J]. Automation of Electric Power Systems，2009，33（18）:23-27（in Chinese）.

[13]FU Yong，SHAHIDEHPOUR M.Fast SCUC for largescale power systems[J].IEEE Trans on Power Systems，2007，22（4）:2144-2151.

[14]LIU Cong，SHAHIDEHPOUR M，LI Zuyi，et al.Component and mode models for the short-term scheduling of combined-cycle units[J].IEEE Trans on Power Systems，2009，24（2）:976-990.

[15]徐帆，姚建国，耿建，等.考虑联合循环机组的机组组合问题[J].电力系统自动化，2010，34（8）:39-43. XU Fan，YAO Jianguo，GENG Jian，et al.Unit commitment problem with combined cycle gas turbine[J].Automation of Electric Power Systems，2010，34（8）:39-43（in Chinese）.

（编辑冯露）

Maintenance Cost Optimization for Combined Cycle Gas Turbines

ZHANG Yantao1，SU Feng2，WANG Yang2，XU Fan1，DING Qia1，TU Mengfu1
（1.NARI Technology Co.，Ltd.，Nanjing 210061，Jiangsu，China；2.North Subsection of State Grid Corporation of China，Beijing 100053，China）

In order to accurately calculate the generating cost of the combined cycle gas turbine（CCGT），this paper introduces the maintenance cost model of CCGT based on the traditional model.The difficulty of this model is that the startup and operation maintenance cost does not coexist in the same calculation period.For this purpose，first we can computer the start-up maintenance cost by superposing it to the mode transition cost，and then by analyzing whether the gas turbine of CCGT starts up in the calculation period we can determine whether to add operation maintenance cost to the target cost. Meanwhile，we can transfer the non-linear expression to the linear expression by linearization techniques and establish the mixed integer linear program.This paper uses the actual data of Macau for testing.The testing shows that the model can effectively solve the maintenance cost of CCGT with more reasonable results.

combined cycle gas turbine；mixed integer linear programming；start-up maintenance cost；running maintenance cost；mode transition

1674-3814（2015）06-0006-06

TM734

A

国家高技术研究发展计划（863计划）资助项目（2012AA050207）。

Project Supported by National High Technology Research and Development Program of China（863 Program）（2012AA050207）.

2015-02-06。

张彦涛（1980—），男，硕士，工程师，研究方向为电力系统运行与优化；

苏峰（1983—），男，博士，工程师，研究方向为电力系统运行与优化；

汪洋（1983—），男，博士，工程师，研究方向为电力系统运行与优化。