基于状态检修的输变电设备故障率的计算

孟昭军，朱兴兴（.南京南瑞集团公司，江苏南京06；.河海大学能源与电气学院，江苏南京00）

基于状态检修的输变电设备故障率的计算

孟昭军1，朱兴兴2
（1.南京南瑞集团公司，江苏南京211106；2.河海大学能源与电气学院，江苏南京211100）

在全状态集成法的基础上提出了求解设备故障率的新方法：等效状态评分法。以设备等效状态评分为模型，模型参数随着设备所经历的过程变化而变化。通过对经历过检修后的状态评分的折算，表征出检修对设备故障率的影响，求得设备可能的故障率。最后，通过算例运用等效状态评分法求解设备的模型参数和故障率，等态状态评分法和全状态集成法的计算结果相同。与全状态集成法相比，等态状态评分法简化了计算，并且物理意义更加明确。

状态检修；故障率；等效状态评分法

电网设备的运行状况对电力系统的安全可靠性影响重大。设备故障往往会造成用户停电，导致直接的经济损失，且需要花费大量的时间和费用进行维修。因此，对于电网设备应采用科学合理的检修体制，提高检修的针对性和有效性，发现问题于萌芽状态并及时解决，从而保障系统的安全性和供电的可靠性，为电网创造更多的经济效益和社会效益。电网设备状态检修正是在这一需求下发展起来的[1]。

不同国家及不同电力企业（如英国EA公司[2]、加拿大Kinectrics公司[3]）对设备健康状态评分时采用的评价模型是有区别的，因此，会得到不同的状态故障率模型。

本文首先回顾了国家电网公司输变电设备状态检修故障率的计算，指出了国家电网公司状态检修设备故障率模型的不足。然后介绍了基于全状态集成法的设备故障率的计算。由于全状态集成法存在着计算量大、物理意义不明确等缺点，在此基础上提出了基于等效状态评分法的设备故障率的计算方法。该方法能够体现停电检修对设备故障率造成的影响，物理意义明确，弥补了全状态集成法的不足。最后，用算例验证了本文提出的等效状态评分法模型和方法的有效性。

1　国家电网公司输变电设备状态检修故障率的计算

国家电网公司《输变电一次设备状态评价标准体系》中给出了基于状态检修的设备故障率的模型λ=Ke-CS。其中，S为设备状态评价的评分值。通过一定的现场统计继而利用反演法计算出模型参数K、C[4]。

国家电网公司提供的输变电设备故障率的计算是利用反演法计算求得，概念清晰，计算简便。然而反演法存在一些固有的缺陷。

1）计算误差大。反演法需要确定样本数据的统计时间，若统计时间较短，由于电力设备属于高可靠性设备，统计样本的故障率统计值会偏低，造成模型参数误差较大；若统计时间较长，统计时间段内设备的状态会发生较大变化，而反演法只考虑统计时间段内某一时刻的状态分值，会造成模型参数较大的计算误差[4]。

2）未考虑检修对设备故障率的影响。同一个设备在不同阶段经过状态检修后即使拥有相同的健康状态评价分值，其故障率也会有所差别。

2　全状态集成法

文献[5]提出了基于完整健康过程的全状态集成法。对于经历了停运检修的设备来说，它的完整健康过程是指从设备重新投运开始到出现结束标志的整个过程。对于未经检修就投入运行的设备来说，它的完整健康过程是指从投运开始到出现结束标志的整个过程。设备的完整健康过程有2种结束标志。

设备故障：从新设备投运、停电检修或者消除故障后重新投运到出现故障。图1中A点设备发生故障，立即安排停电检修，寿命T1为一个健康过程。

设备处于异常或严重状态：从新设备投运、停电检修或者消除故障后重新投运到设备状态评分处于异常或者严重状态，并根据检修要求允许延长一段时间td（td=t8-t6）。图1中B点对应的t6时刻，状态监测显示设备有缺陷，状态评分处于异常状态，在C点对应的时刻t7安排检修。在这种情况下，虽然并未立即进行停电检修，但设备已经处于设备失效过程中，且离真正的失效时刻F点对应的役龄t8很近，相对于较长的整个完整健康过程来说，t8-t7这段时间可以忽略。如图1所示，T2为一个完整健康过程。

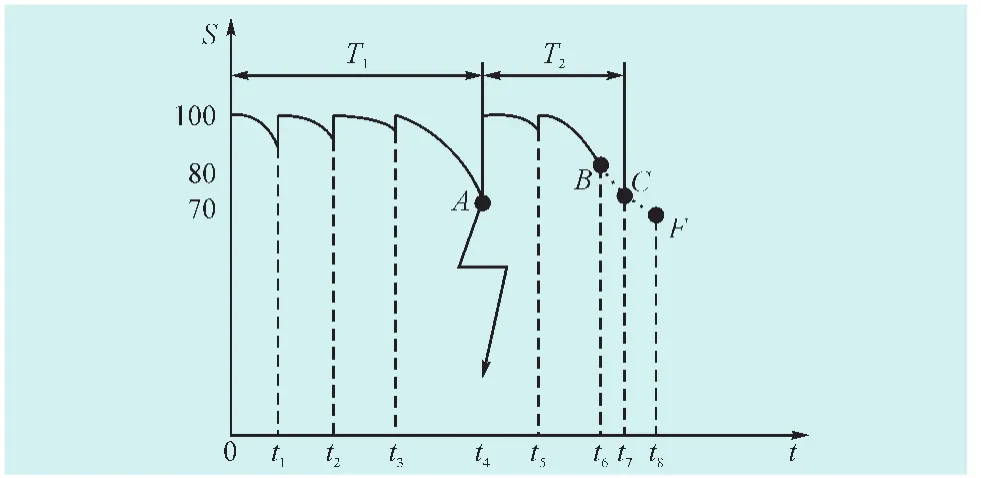
图1　设备完整健康过程示意图Fig.1Diagram of integral health processes for the equipment

设备处于异常或者严重状态时，应适时安排停电检修，因而完整健康过程的结束标志从本质上讲均为停电检修。

图1为设备完整健康过程的示例，其中S为设备的状态评分，t为设备的役龄（时间，一般以年或月为单位）。0点时刻设备投入运行。如图1所示的t1、t2、t3和t5时刻，状态监测显示设备的存在缺陷，安排带电检修或者自行消缺使设备的状态评分重新恢复到100分。设备处于异常状态时应适时安排停电检修，设备处于严重状态时应尽快安排停电检修。图1中所示的t7时刻进行了停电检修，而t4时刻是设备故障。

在实际工程应用中，相邻2次状态评分之间存在着一定的时间间隔，所得到的完整健康过程中的测量数据为离散值。图2示例的完整健康过程拥有7个离散的状态评分值。将相同状态评分的持续时间相加，并按状态评分的大小倒序排列便可得到该图。令p≥1，为整数，表示设备所经历的完整健康过程的序号；令i≥1，为整数，表示相同状态评分按降序排列后的序号。Sp，i为设备处于完整健康过程p、降序排列序号i时的状态评分。图中Sp，i对应的持续时间即为Tp，i，Tp，i可直接从现场跟踪数据得到。

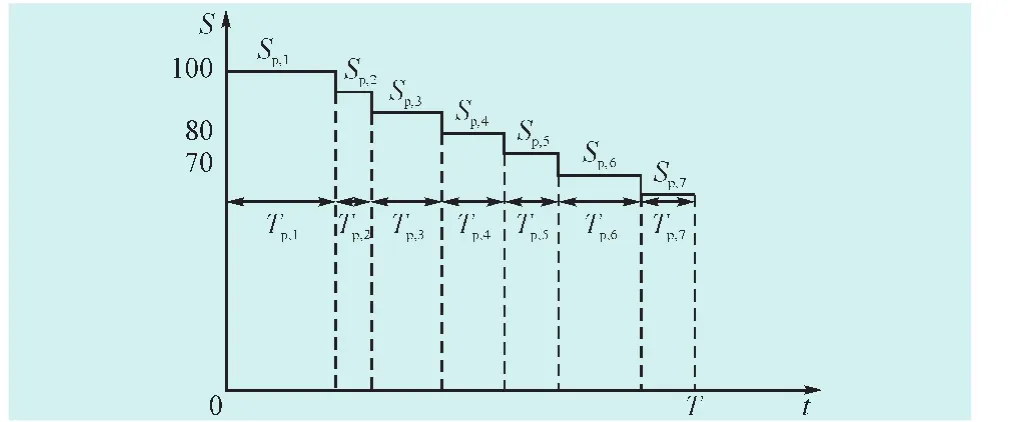
图2　一个拥有7个不同状态评分的完整健康过程Fig.2An integral health process with seven condition scores

全状态集法利用设备的一个完整健康过程的全部状态信息，把各个状态评分的持续时间统一折算到时间轴上的期望时间，计算得到完整健康过程对应的设备全状态集成法的故障率模型参数，然后对所有样本得到的基于完整健康过程的全状态集成法的故障率参数进行研究。基于此，文献[5]提出了一种考虑不同完整健康过程（以下简称过程）中的状态评分对设备故障率影响的改进模型：

式中：Kp为设备所经历的过程p全状态集成法的故障率模型比例参数；Cp为设备所经历的过程p全状态集成法的故障率模型曲率参数；λp，i为状态评分为Sp，i时的设备故障率。

设备的故障类型根据故障诱因的不同可以分为必然性故障和偶然性故障。必然性故障是由内部原因引起的，与设备的状态评分变化情况相关；而偶然性故障是由外部原因（如人员误操作，保护不正确动作、检修质量不良等）引起的。设备的偶然性故障率可以通过统计得到，为常数λ0。对于任意过程，当设备在状态评分为满分100分时发生故障，可以认为就是偶然性故障引起的。因此，过程p对应的比例系数与曲率系数间的关系满足：

为继续求解设备处于过程p时的全状态集成法的故障率参数，文献[5]说明了以下几个概念和定义。

1）时间标准轴T0。它指设备在状态评分为满分100分时的设备期望健康寿命，即假设设备不发生状态变化一直维持满分状态运行直至偶然性故障发生所经历的时间，满足：

因此，时间标准轴T0的大小由偶然性故障率决定。

2）设备在状态评分为Sp，i时的期望状态寿命T（Sp，i）。它是指假设设备以状态评分Sp，i投运并保持该状态运行直至发生故障停运期望的时间，中间不经历任何其他状态，期望状态寿命T（Sp，i）满足：

与T0不同，T（Sp，i）既会受到偶然性故障因素的影响，也会受到与状态评分Sp，i相关的必然性故障因素的影响。

3）基于时间标准轴的折算系数m（Sp，i）。它指设备状态评分为100分时的期望健康寿命T0与状态评分为Sp，i时的期望状态寿命T（Sp，i）的比值，即

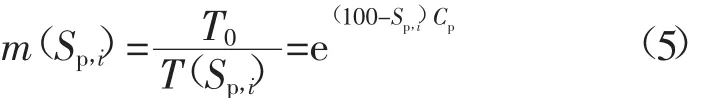
由于式（5）中过程p是可以确定的。所以基于时间标准轴的折算系数m（Sp，i）只与Sp，i状态评分有关，仅随Sp，i变化。引入基于时间标准轴的折算系数的目的是将包含必然性故障因素的期望状态寿命折算为只有偶然性故障因素影响的期望状态寿命。

4）设备实际维持状态Sp，i在标准时间轴上的期望状态持续时间Tp0i。如图3所示，它是将状态评分Sp，i的实际持续时间经时间标准轴的折算得到的时间标准轴上的期望状态持续时间。其值为:

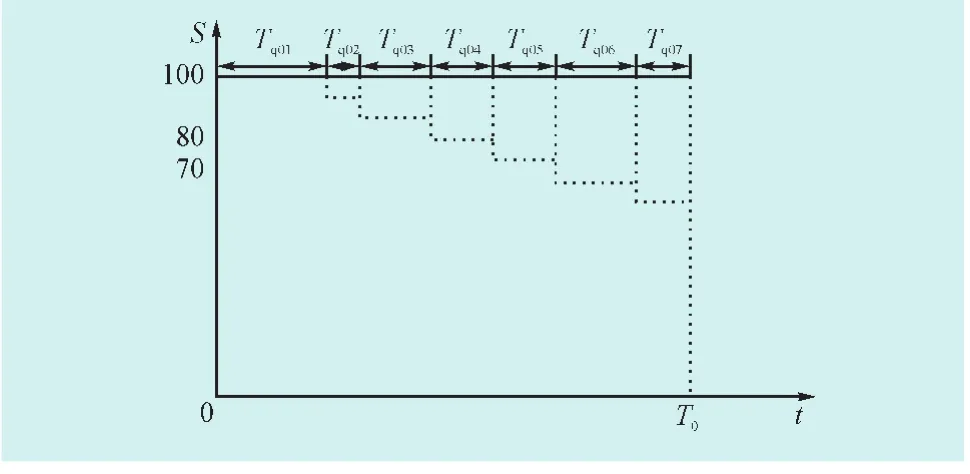
图3　状态评分在标准时间轴上折算所得的期望状态持续时间Fig.3The expecting life time converted into standard time axis for condition scores

若把每个过程中所经历的各状态评分实际持续时间都进行基于时间标准轴的折算，就能得到标准时间轴上各状态评分对应的只受“偶然性故障因素”影响的期望状态持续时间。一个过程对应的所有只考虑“偶然性故障因素”影响的期望状态持续时间累加起来的过程寿命，应该等于由偶然性故障率决定的时间标准轴T0：

由式（5）、式（6）和式（7）可得：

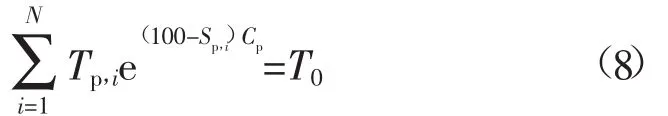
由式（8）就可以解出该设备处于过程p时的模型曲率系数Cp，再将结果代入式（2），便可解得该设备处于过程p时的模型比例系数Kp。进而可以求得不同状态评分对应的设备故障率。

全状态集成法计算结果精确，然而，也存在着一些固有缺陷：

1）计算过程繁琐。应用全状态集成法，必须将每个过程所对应的Kp，Cp，计算出来，所需要计算量较大。

2）物理意义不明确。设备经历了停电检修后，即使拥有相同的状态评分，所对应的设备故障率也应该是不同的，利用全状态集成法计算故障率不能体现出停电检修对设备故障率的影响。

3　等效状态评分法

关于基于状态检修的输变电设备故障率的计算问题，本文提出了等效状态评分的概念，并利用等效状态评分法求解设备的故障率。其中基本假设为：

1）设备在原始状态评分为100分时对应的故障率为设备的偶然故障率。

2）设备工作在初次投运时处于设备的磨合期阶段，其余过程则工作在偶然故障率阶段。

3）初次投运之前没有经过停电检修，因而以设备初次投运后所经历的第一个过程中的原始状态评分作为基准状态评分。过程1的原始状态评分与其等效状态评分相等，其余过程的等效状态评分与基准状态评分之间存在线性关系。

等效状态评分法的具体步骤如下：

①统计设备的偶然故障率、各个过程的原始状态评分以及对应的持续时间。

②利用全状态集成法计算出过程1的全状态集成法的故障率模型参数K1、C1，全部过程的等效状态评分法的故障率模型参数均与过程1相同。

③求解出对于每一个过程的等效状态评分模型，并利用求得的等效状态评分模型求出设备的故障率。

其中，步骤③的算法包括以下内容：

1）求解出等效状态评分模型。为了体现停电检修对设备的影响，需求出设备在不同过程相同原始状态评分以过程1状态评分作为基准的等效状态评分。等效状态评分模型：

式中，ap为过程p的等效状态评分模型比例系数；bp为过程p的常数项；S′p，i过程p的等效状态评分。

过程1的原始状态评分等于等效状态评分，即过程1的等效状态评分模型满足a1=1，b1=0；对于其余过程，采用以下方法求解等效状态评分模型：

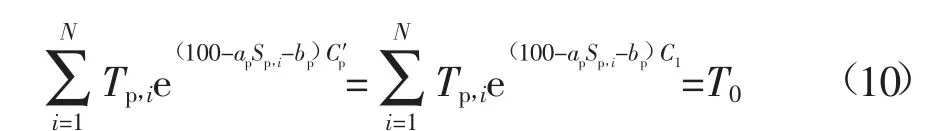
由文献[5]可知，设备状态评分为100分时对应的故障率为偶然故障率，为固定值。因而每个过程原始状态评分为100分的等效状态评分仍为100分，则有：

联立式（10）、式（11）可以解得等效状态评分模型。

2）求解设备的故障率。将步骤②求得的过程1对应的全状态集成法的故障率参数K1、C1和步骤③求得的等效状态评分模型带入下式可求得基于等效状态评分的设备故障率为：

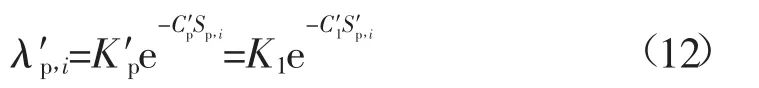
4　算例分析

以华东电网220 kV变压器为例[6]，根据变压器故障记录以及变压器近几年的健康状态评分值数据，得到6个完整健康过程的数据样本，它们对应的役龄标记分别是2，5，8，13，16，20（注：单位为年）。需说明的是，由于状态检修管理工作刚起步，状态评分数据还较少，征求状态检修管理人员的意见后，认为可以用维修记录或者缺陷记录来补充，因此，算例中的健康状态评分值有一定的粗糙性。其中偶然故障率按0.007 28计算。表1示例了一个役龄为20年的变压器状态评分参数。

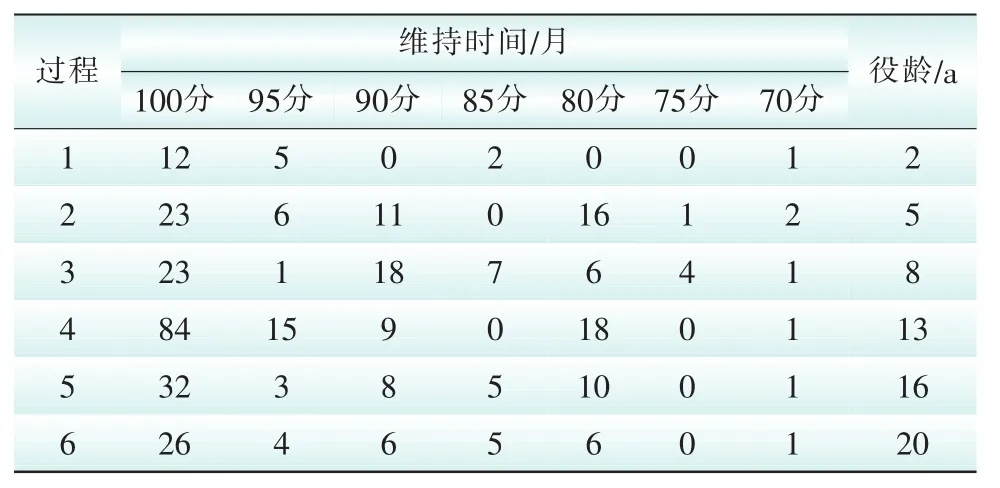
表1　某220 kV变压器状态评分参数Tab.1Parameters of condition scores for a220 kV transformer

给出参考值，K取8 640，C取0.159 58。

首先代入过程1数据，联立等式

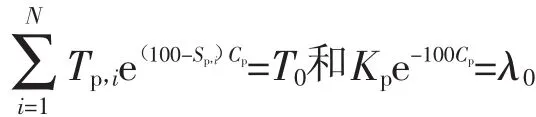
解得结果如表2所示。

表2　过程1的模型参数Tab.2Model parameters for process 1

利用过程1求得K、C，代入等效状态评分法，求解其余过程的等效状态评分模型参数如表3所示。

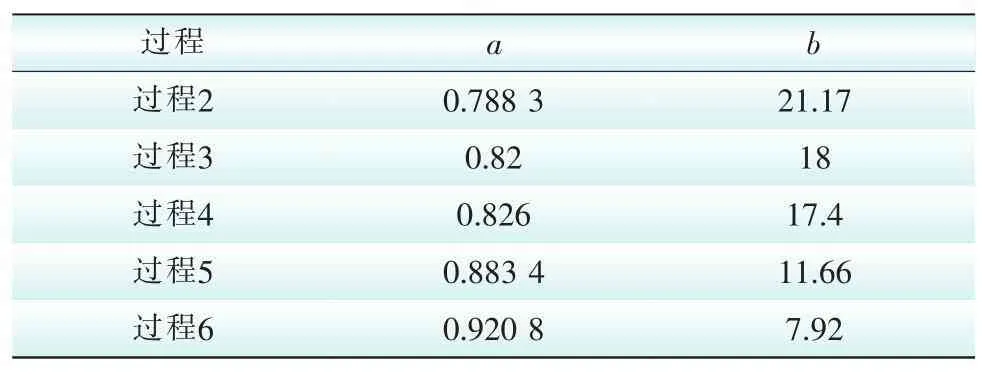
表3　等效状态评分模型参数Tab.3Parameters of the equivalent condition score model

将剩余过程的健康值代入，计算出等效状态评分，从而可以得到设备不同过程不同健康指数下的故障率。

当设备健康值为95时，正好在良好状态与正常状态的交界点，具有一定的代表性。把基于全状态集成法的等效状态评分法计算的参数代入改进模型中，得到的故障概率如表4所示。

表4　95分时各个过程折算后求得的故障率Tab.4Failure rates calculated through converting the condition score of 95 in every process

由中国电力企业联合会统计得到的220 kV变压器的故障率在1.30×10-2（台·a）-1到2.80×10-2（台·a）-1之间[7]，也就是说基于全状态集成法的等效状态评分法计算得到的结果符合统计数据。

5　结语

本文对基于全状态集成法的输变电设备故障率的计算提出了改进，由于采用了检修前后状态评分的等效，简化了计算，体现了停电检修对设备故障率的影响，因此改进模型更为合理。还提出了采用等效状态评分法进行模型参数估算，该方法对设备所经历的完整健康过程进行研究，不仅能最充分地利用状态信息，而且使每一个完整健康过程的研究结果都带有停电检修影响的标记。由于该方法没有对设备的统计时间做出规定，所以样本选择灵活。此外，样本越多，改进模型的估算结果就越准确。

等效状态评分法应用的基础是获得设备完整健康过程的全部状态息，即需要对设备的状态评分值进行连续跟踪。然而，当前电力企业实施设备状态评价还处于起步阶段，有些企业每年只对设备状态评价一、二次，或者在设备停电检修前后进行评价，状态评价信息的缺乏必然会影响设备故障率模型的应用及应用的准确度。但是，随着设备状态检修工作的不断深入和推广，该故障率改进模型和等效状态评分法一定能够在设备的可靠性管理工作中产生良好的应用价值[8-12]。

[1]潘乐真，张焰，俞国勤，等．状态检修决策中的电气设备故障率推算[J]．电力自动化设备，2010，30（2）：91-94. PAN Lezhen，ZHANG Yan，YU Guoqin，et al.Prediction of electrical equipment failure rate for condition-based maintenance decision-making[J].Electric Power Automation Equipment，2010，30（2）：91-94（in Chinese）.

[2]BARSALI S，CERAOLO M.Dynamical models of leadacid batteries：implementation issues[J]．IEEE Trans on Energy Conversion，2002，17（1）：16-23．

[3]JAHROMI A N，PIERCY R，CRESS S.An approach to power transformer asset management using health index[J]．IEEE Electrical Insulation Magazine，2009，25（2）：20-34.

[4]国家电网公司．输变电一次设备状态评价标准体系[S]．北京：国家电网公司，2008．

[5]赵婉芳，王慧芳.基于设备完整健康过程的故障率模型参数研究[J].华东电力，2012，40（8）：1346-1349. ZHAO Wanfang，WANG Huifang.Research of failure rate model parameters based on equipment IHP[J].East China Electric Power，2012，40（8）：1346-1349（in Chinese）.

[6]王慧芳，杨荷娟，何奔腾，等．输变电设备状态故障率模型改进分析[J]．电力系统自动化，2011（16）:27-31．WANG Huifang，YANG Hejuan，HE Benteng，et al．Im-provement of state failure rate model for power transmission and transforming equipment[J]．Automation of Electric Power Systems，2011（16）:27-31（in Chinese）.

[7]中国电力企业联合会．2004年220 kV及以上电压等级变压器、断路器、架空线路等13类输变电设施运行可靠性指标[EB/OL]．[2010-01-28].http：//www．tee．org．en4-6eeckekaozt2OO5．

[8]刘振亚.建设智能电网支撑又好又快发展[J].电网与清洁能源，2009，25（9）:1-3. LIU Zhenya.Build strong smart grid as pillar of sound and rapid development[J].Power System and Clean Energy，2009，25（9）:1-3（in Chinese）.

[9]严玉婷，文习山.绝缘子表面泄漏电流在线监测的研究综述[J].电磁避雷器，2005（3）:8-11. YAN Yuting，WEN Xishan.A review about on-line monitoring the leakage current of insulators[J].Insulators and Surge Arresters，2005（3）:8-11（in Chinese）.

[10]程华，徐政．分布式发电中的储能技术[J]．高压电器，2003，39（3）：53－56．CHENG Hua，XU Zheng．Energy storage for use with distribution power generation[J]．High Voltage Apparatus，2003，39（3）：53－56（in Chinese）.

[11]MILLER T J E.电力系统无功功率控制[M].胡国根，译.北京：水利电力出版社，1990.

[12]毕玉森.低氮氧化物燃烧技术的发展状况[J]．热力发电，2000，29（2）：2-9．BI Yusen．Present status of low-NOx combustion technology[J].Thermal PowerGeneration，2000，29（2）：2-9（in Chinese）．

附录

证明：等效状态评分法和全状态集成法计算设备故障率的结果相同。

如前所述，当p=1时，两者计算结果相同。

当p>1时，对剩余的过程以过程1的K1、C1为基础进行原始状态评分的等效，将式（11）代入式（9）可得

将式（13）代入式（8）可得：

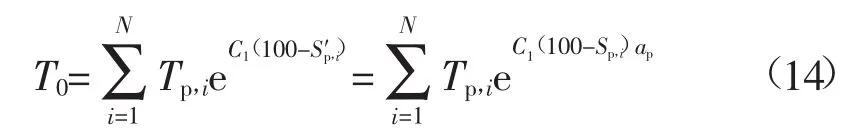
对比式（8）和式（14）可发现：

由式（2）可知

从而由式（16）可得：

将式（15）和式（17）代入式（1）的故障率模型中整理可得：

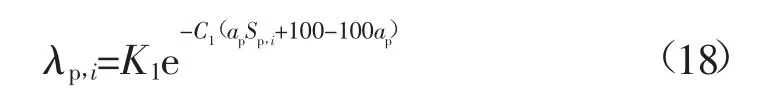
将式（11）代入得：

由此可以推导出利用等效状态评分法求得的设备故障率λ′p，i和全状态集成法求得的设备故障率λp，i相同。证毕。

（编辑冯露）

Calculation of Failure Rate of Power Transmission and Transformation Equipment Based on Condition Maintenance

MENG Zhaojun1，ZHU Xingxing2
（1.NARI Group Corporation，Nanjing 211106，Jiangsu，China；2.College of Energy and Electrical，Hohai University，Nanjing 211100，Jiangsu，China）

In this paper，on the basis of the all-state integration（ASI）method，we propose a new method，namely the equivalent condition score（ECS）method，to calculate the failure rate of the equipment.The proposed method is based on the equivalent condition score model，and parameters of the model vary with the process the equipment has experienced.And through the conversion of the condition scores evaluated after maintenance，we can investigate the effect of maintenance on the failure rate，and then calculate the failure rate of the equipment.The results of the ECS method are the same as those of the ASI method.Compared with the ASI method，the ECS method can simplify the calculation process，and also have more specific physical meaning.

condition maintenance；failure rate；equivalent condition score

1674-3814（2015）06-0015-06

TM614

A

国家高技术研究发展计划（863计划）（2011AA 05A105）；国家电网公司科技项目（计及电网安全稳定性的输变电设备风险评估与运维管理决策技术研究与应用）。

Project Supported by National High Technology Research and Development Program of China（863 Program）（2011AA05A105）；State Grid Corporation of China Technology Project-Research and Applications of Risk Evaluation and Maintenance Decision Management Technologies Considering Power System Stability.

2015-03-03。

孟昭军（1973—），男，博士，研究员级高级工程师，从事电力系统分析与控制、输变电设备状态检修方向的研究工作；

朱兴兴（1990—），男，硕士研究生，从事输变电设备状态检修的研究工作。