一种求解汽车外流场问题的可扩展数值算法

闫争争陈荣亮赵宇波蔡小川，2

1（中国科学院深圳先进技术研究院工程与科学计算研究室 深圳 518055）

2（美国科罗拉多大学博尔德分校计算机系 博尔德 80309）

一种求解汽车外流场问题的可扩展数值算法

闫争争1陈荣亮1赵宇波1蔡小川1，2

1（中国科学院深圳先进技术研究院工程与科学计算研究室 深圳 518055）

2（美国科罗拉多大学博尔德分校计算机系 博尔德 80309）

受外型复杂、雷诺数高等因素影响，汽车外流场流动的数值计算规模巨大且难以精确求解。发展高效并行算法以利用超级计算平台资源来数值求解外流问题成为该领域的研究热点。文章提出一种全隐格式的可扩展并行 Newton-Krylov-Schwarz 算法对某真实汽车的外流场流动问题进行计算。通过与风洞试验以及主流计算流体力学软件的计算结果对比验证了算法的正确性。并行数值计算结果显示，文章的算法在数千处理器规模下仍具有很好的并行可扩展性。

三维非定常不可压缩流动；Navier-Stokes 方程；并行计算；区域分解算法中

1 引 言

在汽车工业中，车体外型的空气动力学分析涉及车辆设计、测试和制造等诸多环节，直接决定了车辆的能耗比、安全性乃至美观性，同时也对乘客的舒适感以及道路周边噪声环境产生重要影响。获取车体外流场流体的流动数据是进行车型气动分析的前提，工程师只有在速度、压力等物理参量的基础上才能通过一系列分析手段得到车型的阻力系数、气动力矩等评价车型的直观数据，因此外流场流动问题对汽车空气动力学研究意义重大。

最初，风洞试验是获取外流场数据的主要技术手段，通过全尺寸或比例模型在风洞中的测试结果来调整实际车型的几何尺寸与构形。根据Buchheim 的经验，开发一款新的车型需要 1000小时的风洞试验［1］，显然这种方法需要非常长的设计周期，严重影响车型定型与市场推广。近二十年来，利用计算机来求解流体流动的控制偏微分方程组，并通过得到的流场来研究流动现象的计算流体力学（Computational Fluid Dynamics，CFD）技术广泛应用于汽车设计领域，现已成为不可或缺的技术手段，其应用程度已经成为评价工程设计先进水平的主要标志［2］。与风洞试验相比，CFD 技术有助于工程师实现数字化、灵活化以及低成本的理想设计模式。

在流体力学中，雷诺数 Re 作为一个无量纲量用来表征流体运动中惯性力与粘性力之比，其值越大表明流体运动中对流越占优，控制方程离散后得到的方程组非线性越强，对求解造成巨大困难。而汽车外流场流动为典型的高雷诺数流动，一般大于 106，采用未添加任何近似流动模型进行直接数值求解方法需要极高的时间、空间分辨率。工程应用中普遍采用近似模拟方法将流体运动加以近似或简化，使之可在高性能工作站（一般为十数核处理器）平台上求解。依据假设状况，近似模型方法可归纳为如下几类：

（1）基于统计理论的雷诺平均 Navier-Stokes方程（Reynolds Averaged Navier-Stokes，RANS）方法［3，4］。该方法是当前工程问题中最常用以及应用最广泛的流动模型，其原理是将流动视为平均流动与脉动流动的叠加，流场中的各参数也表示为两者的叠加值。由于引入脉动量乘积等物理量导致方程组的不封闭，因此需添加湍流模型使方程组可解。通过流体力学理论或者实验数据可得到多种不同的模型，如 k-ε 双方程模型、 k-ω双方程模型、Reynolds 应力模型等，需根据实际情况选择合适的模型进行计算。RANS 方法通过近似使得计算量大为降低，但缺点是模型选择依靠经验、计算仿真度较低。

（2）基于流动分解技术的大涡模拟（Large Eddy Simulation，LES）方法［5，6］。大涡数值模拟来源于对流场中不同尺度的涡的识别与归类。其原理是将流动分解为大尺度和小尺度两种运动：大尺度的漩涡具有各向异性特征，是流动的主要表现；小尺度漩涡主要体现能量的耗散情况。在计算过程只使用直接模拟方法计算大尺度涡的运动，小尺度涡则通过近似模型来模拟。这种方法与 RANS 方法相比虽然增加了计算量但却提高了计算仿真度。

（3）脱体涡模拟（Detached Eddy Simulation，DES）方法［7］。脱体涡模拟结合了雷诺时均方法与大涡模拟的优点，简单而言即是在附面层附近使用 RANS 方法，在其他区域使用 LES 方法，其计算量与计算仿真度介于雷诺平均 Navier-Stokes方程与大涡模拟两者之间。

仿真度与计算能力始终是个不可调和的矛盾，要想达到可信的仿真度就必须细化网格以精确描述流体的流动特征。CFD 技术的核心是求解流体控制方程经有限元等方法离散后所形成的稀疏方程组。实际计算中，该稀疏方程组的规模十分巨大且伴随着强烈的非线性，求解异常困难。近年来，大型并行计算机的出现为计算能力提供了有力的保障，研究适用于求解大规模非线性稀疏方程组的高可扩展并行算法，并使之与计算机硬件资源匹配，已经成为计算机辅助工程领域非常重要的研究方向［8］。

为获取流场的高分辨率数值结果，本文采用未添加流动近似模型的全 Navier-Stokes 方程方法。该方法庞大的计算量对计算机的硬件与算法都有极高的要求。本文基于国家超级计算深圳中心的曙光星云超级计算平台，通过对大规模非线性系统进行高效求解器和预处理技术的研究，提出一种可扩展并行 Newton-Krylov-Schwarz（NKS）算法。非线性方程采用非精确Newton 方法进行求解，在每个 Newton 步，Jacobian 系统通过基于区域分解的限制加性Schwarz 预条件子处理后，使用以广义最小残量（Generalized Minimal RESidual，GMRES）方法为代表的 Krylov 子空间迭代法作为线性求解器进行求解。为验证算法，本文首先对障碍物绕流标准问题进行研究，所获得的流场数值结果与风洞试验数据及商业软件计算结果进行对比。随后，作为应用，我们对某真实汽车的外流场问题进行计算。数值结果显示，本文提出的算法计算所得流场数值相较于采用近似流动模型的 RANS方法所得结果更为精确。算法的并行测试结果显示，本文的算法在扩展至数千个处理器平台时仍具有非常良好的可扩展并行性能。

本文的结构如下：第一节简要介绍汽车外流场的数值模拟技术的现状与趋势；第二节对流体控制方程及本文采取的有限元离散格式进行介绍；NKS 算法描述以及相关数值试验分列于第三、四节；最后在第五节做出总结与展望。

2 流体控制方程及其有限元离散

2.1 流体控制方程

数值模拟技术通过计算流体控制方程以获取流体运动区域的离散解，汽车周围流体流动速度一般低于 0.3 Ma，可视为不可压缩 Newton 流，因此采用三维非定常不可压 Navier-Stokes 方程描述汽车外流场流动：

以及边界条件：

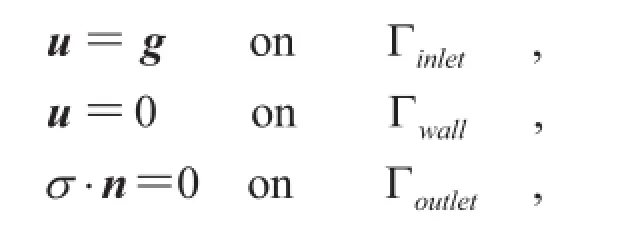
2.2 控制方程离散

为了获取流体流动数值解，数值模拟技术通过将控制偏微分方程按照某种离散格式离散，然后转化为各个计算节点上的代数方程组，最后求解得到各节点上的值来获取整体流场的近似解，因此离散化与代数化是数值计算的前提。对于本文的瞬态问题，偏微分方程的离散在空间和时间上都有体现，选取合适的时空离散格式对后续求解算法有重要影响。

空间离散的具体实现形式分为两方面：在数学上是对控制方程的空间项采用一定数值格式使之代数化；在物理模型上是根据数学离散格式的要求进行计算区域的网格剖分。考虑到高阶的有限元虽然在计算精度上有所提高，但其在离散化后所形成的矩阵中非零元素过多，从而影响算法整体的并行可扩展性。结合并行计算的特点，我们采用低阶的 p1-p1有限元格式对空间进行离散。计算网格主要分为结构化网格与非结构化网格两种类型。结构化网格对复杂几何外形适应性较差，因此难以用于车辆外流场等复杂的实际工程问题。而非结构网格中节点与单元可控性强，可根据问题对网格密度进行优化处理，提高网格的质量，目前已成为诸多工程问题普遍采用的网格类型。

有限维试函数及全函数空间可以表示为：

多数空间离散时通常按照物理量排列，此类按照各相关变量（压力、速度）的排序方式会在结构上影响最终求解的 Jacobian 矩阵，呈现出鞍点结构，不利于并行计算。本文中，空间离散按照单元顺序排列方法构造。此方法作为预条件子，在后续的区域分解过程中将原有整体的鞍点结构分散在局部的子矩阵中，减少子区域间共享的变量数量，从而减少通信量，保证了并行效率。

时间项方面，本文采用了全隐格式进行离散。由于全隐格式减轻甚至消除了 CFL 条件对时间步长的限制，在进行大规模数值计算时具有一定优势。具体地，针对上述不可压缩 Navier-Stokes 方程，选取隐式向后 Euler 有限差分格式对时间项离散，即将控制方程（1）离散为如下非线性代数方程：

其中，Δt为时间步长；S(xn)为在第 n 时间步经空间离散后形成的半离散系统。至此，问题化解为在每个时间步求解非线性方程组：

3 并行 Newton-Krylov-Schwarz 算法

在每个时间步内，经有限元离散后形成的系统（3）规模十分巨大，且因对流占优而具有很强的非线性。求解此类大规模的病态问题时，一般均需借助大型并行计算机及相应的可扩展性算法。实际上，多数基于偏微分方程的工程应用与科学计算问题，如污染扩散模拟、数值天气预报等，最终都会形成稀疏的线性或非线性方程组。由于在现实生活中这些问题多以非线性的方式存在且往往规模巨大，因此大规模稀疏非线性方程组的求解方法成为数值计算领域的研究热点。非线性方程组的求解通常包含线性化、线性求解器构造以及预处理等多个步骤，本文据此进行相关非线性方程组求解算法的研究。

目前非线性方程组线性化方法中最常用且有效的是 Newton 类方法。Newton 类方法具有结构简单、自校正等诸多优点，已广泛应用于工程与科学计算各个领域。Newton 类方法包括精确 Newton方法、拟 Newton 方法以及非精确 Newton 方法三种主要类型。精确 Newton 方法需要对 Jacobian 矩阵进行精确求解，因此该方法收敛速度最快，但当问题规模较大时，整体的计算量非常巨大，计算成本高且计算效果差。Newton 方法一般只要进行若干次迭代即可达到收敛精度，为了保留此优点，虽然可以构造更高收敛阶的方法，但许多数值算法还是在 Newton 方法基础上改进 Jacobian 矩阵处理方式以提高求解的性能。其中，拟 Newton 方法通过将 Jacobian 矩阵近似为易于求解的其他矩阵，从而达到减少整体计算量的目的。某些情况下，拟 Newton 方法中近似矩阵的求解成本依然较高。而非精确 Newton 方法虽然需要求解原始的 Jacobian 矩阵，但是不需要精确求解，而是通过调节求解精度来达到计算量与收敛速度的平衡。

求解大规模稀疏线性方程组分为直接法与迭代法两类。直接法按照元素或行处理矩阵，以矩阵分解或消去为手段，具有高精度、高稳定性等优点，在求解规模较小的问题时能达到快速求解的目的。然而，当计算规模增大时，如浮点运算次数、所需存储量等计算成本开销大幅增加。随着三维有限元网格高分辨率的要求，自由度以千万为量级的问题愈加平常。因此在计算超大规模系统时，直接方法已不现实。而迭代法能够以较小的计算机存储及开销代价求解大规模的问题，且相较而言其在并行求解中比直接法具有更易控制的优点，因此迭代法得到广泛的应用，已经成为求解大规模非线性方程组的不二选择。目前 Krylov 子空间迭代方法具有占用内存小、求解速度快等优点而被广泛作为线性解法器。

无论是在线性还是在非线性迭代法中，预条件子都起到加速收敛的作用，在数值算法构造中占据重要地位。其作用是以较低的额外代价换取迭代次数的大幅降低和求解时间的有效减少，预条件子的构造往往依赖于所研究的物理问题［10］，对预条件子的改进是提高整个数值算法性能的关键。Dryja 等［11］的研究表明，区域分解方法既可以作为迭代法也更适合于作为其他高效迭代求解器的预条件子。同时区域分解预条件子由于其“分而治之”的特点，尤其适合于当前流行的分布式并行计算机环境。

基于上述方法，本文提出了求解汽车外流场问题的 NKS 算法。使用非精确 Newton 算法作为非线性求解器，在每个非精确 Newton 步里使用由基于区域分解方法的 Schwarz 预处理算子来加速Krylov 算法求解 Jacobian 方程。其详细步骤如下：

（1）使用前一个时间步的解作为初始值

（2）对 k=0，1，… 执行以下步骤，直至收敛：

① 构造 Jacobian 矩阵；

在本研究中，我们使用该算法求解 2.2 节中控制方程离散后形成的非线性系统（3）。

本章介绍的算法基于阿贡国家实验室开发的开源可移植并行软件包 PETSc（Parallel Extensible Toolkits for Scientific Computing）［13］实现。PETS基于基础线性代数子程序库 BLAS、线性代数包LAPACK 以及消息传递接口库 MPI 等构成线性求解器、非线性求解器以及时间步进积分器三个主要的组件，为用户提供了包括求解大规模稀疏线性方程组的多种 Krylov 子空间方法在内的丰富的算法以及预条件子，在高性能计算平台上具有强大的偏微分方程数值求解能力。目前 PETSc已经成功应用于优化问题、生物医学、计算流体动力学等多类工程与科学计算问题。

本文的数值算法的应用算例在国家超级计算深圳中心的曙光星云超级计算机上展开。该计算平台的科学计算分区拥有 640 个计算节点，每个节点配置双路六核心 Intel 5650@2.76 GHz 处理器与 24 GB 内存，共计 7680 个 CPU 处理核心，网络互联方式为 InfiniBand4 万兆网络，操作系统为 Linux。

4 数值算例

在本节，我们采用 NKS 算法所获取的结果与风洞试验以及计算流体力学程序包 CFX 的计算结果进行对比来验证算法的正确性。

与大多数计算流体力学程序包采用有限体积方法不同，CFX 采用了基于有限单元的有限体积方法，在保证单元的守恒特性的基础上结合了有限元方法的精确特性。CFX 提供了隐格式的求解技术，改进了“压力项假设-求解-修正压力项”的传统迭代算法，增加了计算的稳定性与收敛速度。为使实验结果具有可比性且有对比价值，NKS 与 CFX 进行数值计算时均采用同样的几何模型、流体材料属性、计算区域、有限元网格以及初始和边界条件。

4.1 障碍物绕流标准问题

为了支持和开展基于高性能计算机的流体数值模拟研究，德国研究基金通过优先支持项目资助了多种典型流动的数值模拟研究工作。通过开展大量的风洞试验获取相关流场信息，为验证数值模拟算法提供了丰富有效的对比数据，障碍物绕流问题便是其中之一。车辆的外部流场属于典型的绕流问题，我们采用 NKS 算法对其中两类绕流标准问题进行计算，所获取的结果与风洞试验以及 CFX 的计算结果进行对比来验证算法的正确性。

4.1.1 障碍物标准绕流问题模型

本小节的数值算例为圆柱体与长方体外部绕流［14］，如图 1 所示。

图1 障碍物标准绕流问题模型及计算区域尺寸Fig. 1 Dimensions of the obstacles and the computational domain

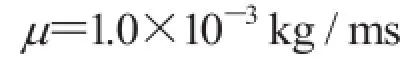
本例中 Newton-Krylov-Schwarz 算法各参数设置如下：线性与非线性相对误差分别设置为1.0×10-4和 1.0×10-6；CFX 中，采用二阶向后Euler 格式对时间项进行离散。残差收敛条件设置为均方根误差设为 1.0×10-6，在 16 核处理器条件下进行计算。

4.1.2 流场数值结果

在外流场分析中，气动力及其系数如阻力系数 Cd、升力系数 Cl等是衡量气动性能的最重要的参数，气动力的计算公式如下：

阻力 Fd：

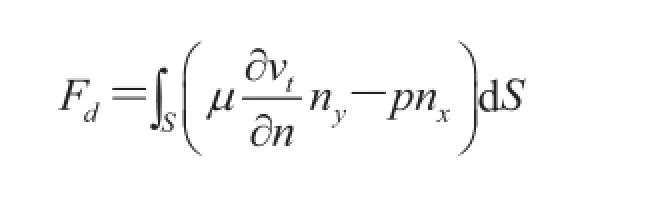
升力 ：

其中，S 为障碍物表面积；nx、ny分别为 S 在x、y 方向的法向分量；vt为速度沿着 S 的切向向量方向的分量。

与阻力及升力相对应的阻力系数 Cd与升力系数 Cl定义如下：

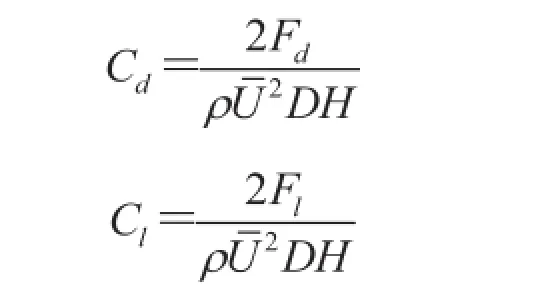
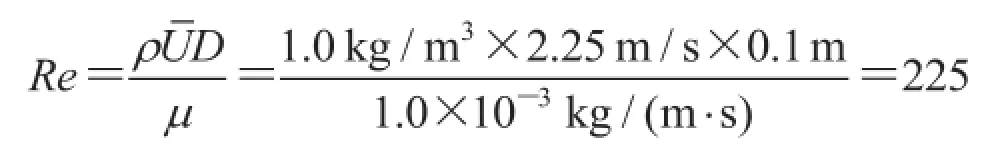
可见标准绕流问题的雷诺数较低。

为了对比其他流场信息，除了气动系数外，我们还在障碍物迎风面及背风面设置两个观测点 a（xa，ya，za）=（0.45，0.20，0.205）与 b（xb，yb，zb） =（0.55，0.20，0.205），使用两点间压力差= P（xa，ya，za，t）-P（xb，yb，zb，t）来观测与对比流场的数值结果。对于两个障碍物算例，本文对比了其稳态与瞬态两种情况，列于表 1。

表1 障碍物绕流测试算例Table 1 Test cases of flow around the obstacles

NKS、CFX 以及风洞（Wind Tunnel，WT）试验对比结果列于表 2。从对比结果可以看出，本文提出的算法与商业软件计算结果接近，同样都在风洞试验所得数据误差范围之内，证明了数值方案以及算法的正确性。

表2 针对障碍物扰流问题 NKS 算法、CFX 以及风洞试验结果对比Tables 2 Comparison of the NKS algorithm， CFX and wind tunnel for the benchmark problems

4.1.3 并行可扩展性结果

本小节给出基于 NKS 算法计算圆柱形障碍物标准绕流问题的并行可扩展性结果。两套不同规模的网格，分别约含 5.1×106个四面体单元（DOF =3.6×106）和 1.3×107个四面体单元（DOF= 9.1×106），被用于可扩展性的测试。取固定时间步长，NKS 算法中线性与非线性相对误差分别设置为 1.0×10-6和 1.0×10-12。为减小计算量，取前 20 时间步数值结果的平均值。

表 3 列出了不同处理器条件下计算的可扩展并行计算数值结果。其中，np为处理器个数；Newton、GMRES 和 Time 分别表示为每个时间步内非线性迭代次数、线性迭代次数以和计算时间（单位为秒）。

表3 障碍物绕流问题中 NKS 算法的并行性能Table 3 Parallel performance of the NKS algorithm for the benchmark problem

为了更加清晰地展示可扩展性性能，本文将并行计算数值结果以加速比的形式列图 2 中。加速比通常用来衡量并行系统或程序并行化的性能和效果。在本文中加速比是指固定计算规模，以最低核数所需计算时间基准，增加并行处理器个数后计算时间与基准时间之比的倒数。 理想加速比是指线性的加速情况。

图2 障碍物绕流模拟中每时间步的平均计算时间及加速比Fig. 2 The average compute time per time step and the speedup for benchmark problem

并行计算数值结果显示非精确 Newton 方法使非线性迭代次数非常少，非线性迭代次数几乎与处理器个数无关。线性迭代次数随核数的增加而略微增加。计算时间与加速比等数值结果显示，针对低雷诺数问题，在 DOF=3.6×106的算例中，当核数小于 1024 时，并行效率在 65%以上；当核数达到 1024 时，计算效率会有所下降。这并不是算法使然，而是由计算规模不足造成的。当进行分区计算时，如果子区域的规模较小，那么在整体求解时间中，子区域间通信时间所占的比例将会提高，导致计算效率降低。整体而言，本文提出的并行 NKS 算法具有非常好的可扩展性，当处理器个数达到 2048 时并行效率仍在 50% 左右。

4.2 汽车外流场问题

4.2.1 汽车几何模型与计算区域

在分析车型空气动力学性能前，首先需要使用数字化建模技术对原始设计车型进行几何建模。本文采用三维 CAD 软件依据某真实车型全尺寸数据进行模型构造。如图 3 所示，整车长 L =4.6 m，车宽 W=2.0 m，车高 H=1.4 m，轴距B=1.6 m。

图3 汽车三维 CAD 模型及计算区域示意图Fig. 3 The CAD model of car and the computational domain

图4 汽车外流计算网格示意图Fig. 4 A view of the inside of the meshed domain

流体取 25℃ 标准大气压下的空气，密度 ρ= 1.185 kg/m3，动力粘度系数 μ=1.831×10-5kg/ms。设进口速度 Vin=30 t，时间步长=0.01 s，计算1 s 内流场的变化情况。算法中的线性和非线性求解器的相对收敛误差分别取为 10-4和 10-6。分别取 =30 m/s 为特征速度，车高 H=1.41 m为特征长度，计算雷诺数

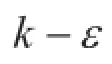
4.2.2 流场数值结果

以阻力系数 Cd为代表的空气动力学系数是影响车型设计的最主要参数，设计人员往往据此来评判车型的能耗比以及气动安全性能。本文中首先对 0～1 s 时间内 NKS 算法与 CFX 计算得到阻力系数 Cd进行比较，瞬态数值结果列于图 5。阻力系数对比图显示，两种算法计算得到的阻力系数基本一致。

图5 汽车阻力系数数值结果对比Fig. 5 The comparison of drag coefficient

随后，我们取 t=1 s 时刻两种算法的流场结果进行比较。首先我们比较了车身表面静压（单位为帕），如图 6 所示。

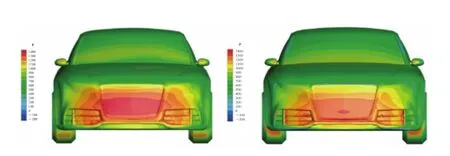
图6 汽车车体前身压力分布对比云图（左：CFX，右：NKS）Fig. 6 The comparison of pressure contours（left：CFX， right： NKS）

静压的大小与分布与汽车所受的气动力直接相关，NKS 与 CFX 的计算结果均显示车身表面静压呈对称分布。静压高值分布于车体前身、前挡风玻璃、后视镜以及车轮的迎风面。车前身其余部分压力稍高于大气压，车体顶部、车窗与车体边缘处静压在较小。

为了更加直观地观测汽车外流场流体流动情况，本文也给出车体对称面 z=0 m 上的二维流线分布。图 7 描述了 NKS 与 CFX 计算的汽车对称面上的涡流结构。其中，NKS 所计算结果中，在车体前部地面、发动机罩与前挡风玻璃交界处，以及尾部地面上有较明显的涡流，车尾区域亦有数个尺度较小的涡流。而 CFX 计算结果中却无法清晰显示，原因是 CFX 采用了基于统计理论的 RANS 流动模型，相同网格尺寸下其计算精度会有影响。两种算法的结果比较显示，未添加近似流动模型的 NKS 算法可以计算得出更详细的流场信息。

图7 车体对称面二维流线图（上：CFX，下：NKS）Fig. 7 Surface streamline patterns on the symmetry plane for the car （upper： CFX， lower： NKS）

4.2.3 并行可扩展性结果

本小节给出基于 NKS 算法求解汽车外流场的并行可扩展性数值结果，实验所取网格自由度约为 1.03×107，Newton 非线性迭代与 Krylov 子空间方法线性迭代收敛误差分别设置为 10-6和10-12，数值结果取前 20 个时间步的平均值。

表4 列出了不同处理器条件下计算的可扩展并行计算数值结果。为了更加清晰地展示可扩展性性能，本文将并行数值结果以加速比的形式列于图 8 中。

表4 汽车外流场模拟中 NKS 算法的并行性能Table 4 Parallel performance of the NKS algorithm for the simulation of flow around car

图8 每时间步平均计算时间与加速比Fig. 8 The average compute time per time step and the speedup for the simulation of flow around car

从并行测试结果可以看到，由于采用了前一时间步的结果作为初始值，每个时间步的非线性迭代次数非常少，非线性迭代次数几乎与处理器个数无关。随着计算核数的增加，线性迭代次数略微增加。计算时间等并行计算数值结果显示，本文提出的算法具有非常好的可扩展性，处理器个数达到 2048 时并行效率仍在 50% 左右。

5 结 论

复杂几何造型、高雷诺数导致汽车外流场的精确数值求解因计算规模巨大、非线性强而极难展开，是目前工程计算领域中非常具有挑战性的问题。本文提出一种并行的 Newton-Krylov-Schwarz 算法来求解控制方程有限元离散后形成的大规模稀疏非线性方程组。基于该算法，本文首先对较低雷诺数的标准绕流问题进行求解，流场结果与风洞试验数据以及 CFX 计算结果进行对比，验证了算法的准确性。随后作为应用，对真实尺寸的汽车外流场流体流动进行数值模拟。流场数值结果以及并行计算数值结果表明，本文提出的算法在数千核处理器条件下仍具有良好的并行可扩展性能。

在本文提出的并行 Newton-Krylov-Schwarz算法中，Newton 型方法严重依赖于初值，选取合适的初值对整体计算的迭代次数与计算时间等并行性能有重要影响［17］。为加快收敛，多水平网格算法是可选择的算法之一，其原理是先在较粗网格获取数值解，再将其插值到较细网格上，作为细网格计算的初值。该算法能够有效地降低非精确 Newton 方法的迭代次数以及各步中的线性迭代次数［18］。因此，下一步研究计划是结合车辆外流场的流动特点，将多水平网格技术应用于大雷诺数非定常不可压缩 Navier-Stokes 方程的求解中，获取更好的并行性能。此外，算法的很多细节，如网格并行分区与管理、通信问题等仍有待于进一步的深入研究。

［1］ 张英朝. 汽车空气动力学数值模拟技术 ［M］. 北京: 北京大学出版社， 2011.

［2］ 阎超， 都彦喆. CFD 技术及其在大飞机研制中的应用 ［J］. 航空制造技术， 2008， 14: 42-44.

［3］ Guilmineau E. Computational study of flow around a simplified car body ［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2008，96（6）: 1207-1217.

［4］ Han T. Computational analysis of three-dimensional turbulent flow over a bluff body in ground proximity ［J］. AIAA Journal， 1989， 7: 1213-1219.

［5］ Krajnović S， Davidson L. Flow around a simplified car， part 1: large eddy simulation ［J］. Journal of Fluids Engineering， 2005， 127（5）: 907-918.

［6］ Howard RJA， Pourquie M. Large eddy simulation of an Ahmed reference model ［J］. Journal of Turbulence， 2002， 3（5）: 1-18.

［7］ Guilmineau E， Chikhaoui O， Deng GB， et al. Cross wind effects on a simplified car model by a DES approach ［J］. Computers & Fluids， 2013， 78: 29-40.

［8］ 邱剑， 顾兆林. 利用高阶分区并行算法实现直接数值模拟 ［J］. 计算力学学报， 2008， 25（1）: 20-24.

［9］ Franca LP， Frey SL. Stabilized finite element method: II. The incompressible Navier-Stokes equations ［J］. Computer Methods in Applied Mechanics and Engineering， 1992， 99: 209-233.

［10］ Knoll D， Keyes DE. Jacobian-free Newton-Krylov methods: a survey of approaches and applications ［J］. Journal of Computational Physics， 2004， 193: 357-397.

［11］ Dryja M， Widlund OB. Towards a Unified Theory of Domain Decomposition Algorithms for Elliptic Problems ［M］. New York: New York University，Courant Institute of Mathematical Sciences，Division of Computer Science， 1989.

［12］ Cai XC， Sarkis M. A restricted additive Schwarz preconditioner for general sparse linear systems ［J］. SIAM Journal on Scientific Computing， 1999，21（2）: 792-797.

［13］ Balay S， Buschelman K， Gropp WD， et al. PETSc Users Manual ［Z］. Argonne National Laboratory，2012.

［14］ Schäfer M， Turek S. Benchmark Computations of Laminar Flow Around a Cylinder ［M］. Vieweg+ Teubner Verlag， Springer， 1996.

［15］ 王夫亮. 侧风作用下的汽车气动特性研究 ［D］.吉林: 吉林大学， 2009.

［16］ Karypis G， Aggarwal R， Schloegel K， et al. ParMETIS home page ［OL］. ［2014-7-9］. http:// glaros.dtc.umn.edu/gkhome/metis/parmetis/ overview.

［17］ Leader JJ. Numerical Analysis and Scientific Computation ［M］. Boston: Pearson Addison Wesley， 2004.

［18］ Smith BF， Bjørstad PE， Gropp WD. Domain Decomposition: Parallel Multilevel Methods for Elliptic Partial Differential Equations ［M］. New York: Cambridge University Press， 1996.

A Scalable Numerical Method for Simulating the External Flows around Cars

YAN Zhengzheng1CHEN Rongliang1ZHAO Yubo1CAI Xiaochuan1，2

1（ Research Centre for Science and Engineering Computation， Shenzhen Institutes of Advanced Technology，Chinese Academy of Sciences， Shenzhen 518055， China ）

2（ Department of Computer Science， University of Colorado Boulder， Boulder， CO 80309， USA ）

The high-fidelity numerical simulation of unsteady flows around cars are a very challenging computational problem because of the huge computation caused by high Reynolds number and complex geometry. In this paper， we presented a scalable parallel Newton-Krylov-Schwarz based fully implicit algorithm for the full unsteady incompressible flows around cars and compared our results with results obtained from commercial CFD software. Our algorithm shows very good parallel scalability on a supercomputer with over two thousand processors.

three-dimensional unsteady incompressible flows； Navier-Stokes equations； parallel computing； domain decomposition method

图分类号 O 246A

2014-04-23

2014-07-09

中国科学院知识创新工程重要方向项目（KJCX2-EW-L01）；广东省科技计划国际合作项目（2011B050400037）

闫争争（通讯作者），博士研究生，研究方向为可扩展并行计算，计算流体力学，E-mail：zz.yan@siat.ac.cn；陈荣亮，助理研究员，研究方向为流体优化算法；赵宇波，正研级高级工程师，研究方向为计算流体动力学数值算法；蔡小川，研究员，研究方向为偏微分方程数值算法与区域分解方法。