基于输出电压校正的混合有源滤波器控制策略

徐永海，温从溪

（华北电力大学 电气与电子工程学院，北京 102206）

0 引言

电力电子装置在电力系统中的应用越来越广泛，由此引起的谐波问题日益严重。安装滤波装置是最常用的减小谐波的方式。混合滤波器结合了无源滤波器（PF）与有源滤波器（APF）各自的优点，具有良好的应用前景［1-7］。

文献［8］提出了一种混合电力滤波器结构，其中PF与负载并联，APF与PF的滤波电抗器并联，该结构能够抑制系统谐振［9-10］，有效减小APF容量，容量减小效果优于APF与PF直接串联的结构［11］，能够有效地应用于大容量场合。针对这种结构的混合滤波器，文献［8］利用比例控制，以系统谐波电流的倍数作为APF输出电压的参考值，文献［9］则将系统电流的倍数作为APF输出电流的参考值，但这2种方法均存在滤波效果与系统稳定性之间相互矛盾的缺陷。文献［11］提出了一种广义积分控制方法，使APF有选择性地进行滤波，提高了谐波滤除率，但动态响应时间较长；文献［12］结合文献［8］和文献［11］给出了一种基于模型的控制方法，相当于是一种广义的比例积分（PI）控制，但控制环节中的PI参数不易确定；文献［13-14］提出了一种有源调谐方法，只采样混合滤波器电流，而不采样系统电流，虽然APF控制不依赖于滤波系统本身之外的电压、电流信息，但对背景谐波的抑制作用较小。

本文提出了一种基于输出电压校正的混合APF控制策略，将APF控制成电压源，在比例控制的基础上，从系统剩余谐波与谐波源产生谐波的相量关系出发，根据系统剩余谐波电流的幅值和初相位，计算出一个正弦信号对APF输出电压参考信号进行校正。采用滑窗迭代离散傅里叶变换（DFT）方法［15］检测系统电流的谐波的幅值和初相位，计算出APF输出电压校正信号的幅值和初相位，仿真证明所提方法参数选择简单有效，具有响应快速、控制误差小的优点，谐波滤除率较高，同时能够在系统中含有背景谐波时达到较好的滤波效果。

1 混合APF的比例控制［8］分析

混合APF结构如图1所示，系统电流h次剩余谐波电流ISh可分为谐波源（系统谐波电压和负载谐波电流）产生的h次谐波电流ISh0和APF产生的h次补偿谐波电流IShAPF，如图2和式（1）所示。

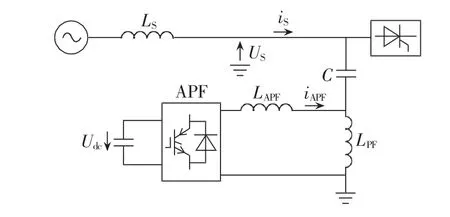
图1 混合APF结构Fig.1 Structure of hybrid APF

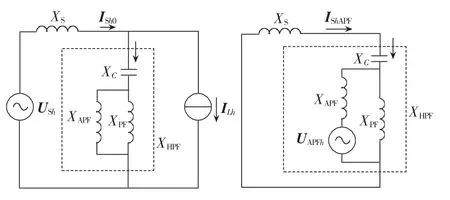
图2 混合滤波器h次谐波等效电路Fig.2 h-order harmonic equivalent circuit of hybrid APF

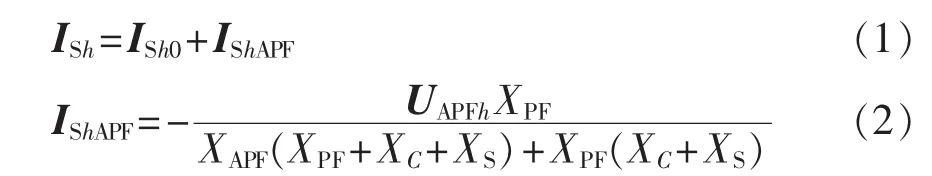
文献［8］提出的比例控制方法是将APF输出谐波电压控制为系统谐波电流的k倍，即给APF的输出电压指令为：

忽略系统电抗、PF和APF输出电感中电阻的影响，假设对于h次谐波，APF输出谐波电压和其产生的补偿谐波电流之间的阻抗呈容性，记式（2）中的阻抗值则根据式（2）和式（3）可得：

根据式（1）可得：

根据式（3）—（5），以逆时针为正方向，可以画出UAPFh、ISh、IShAPF、ISh0之间的相量关系如图 3所示。

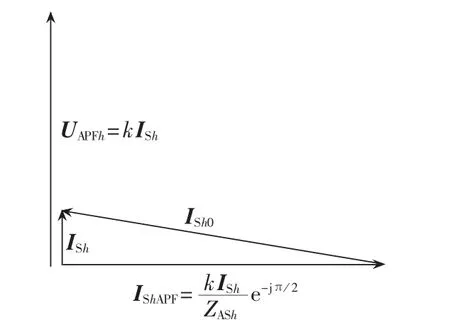
图3 各电流、电压的相量关系Fig.3 Phasor diagram of voltage and currents

根据图3可以计算得到，比例控制下的系统剩余谐波电流满足：

同理可得，在APF输出谐波电压和其产生的补偿谐波电流之间的阻抗呈感性时，比例控制下的系统剩余谐波电流满足：

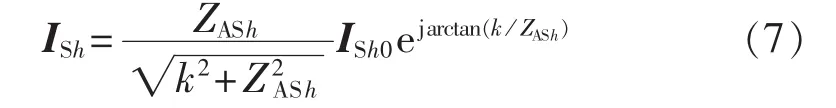
式（6）和式（7）仅在电流方向上有区别，对下文的分析没有影响，因此下文均以式（6）为例分析。从式（6）可以看出，在比例控制下，系统h次剩余谐波的大小取决于比例控制参数k、阻抗值ZASh和谐波源产生谐波电流ISh0的大小，在一定范围内增大比例控制参数k能够减小系统剩余谐波电流，但k增大会使系统稳定性变差；阻抗值ZASh和谐波源产生的谐波电流是无法改变的。

因此，在比例控制的基础上若能控制APF再产生一个与式（6）相匹配的注入供电系统的谐波电流，则能够进一步减小系统剩余谐波电流。

2 基于输出电压校正的混合APF控制策略

2.1 输出电压校正原理分析

在上述分析的基础上，本文提出了基于输出电压校正的控制策略，在比例控制的基础上，在每个工频周期内，以系统剩余谐波电流作为反馈量，计算出一个正弦信号作为下个工频周期APF输出电压的校正信号，以比例控制信号和校正信号之和作为APF输出电压的参考信号，进一步提高系统谐波滤除率。记比例控制信号为UAPFh1，校正信号为UAPFh2，则由UAPFh1和UAPFh2产生的补偿谐波电流为：

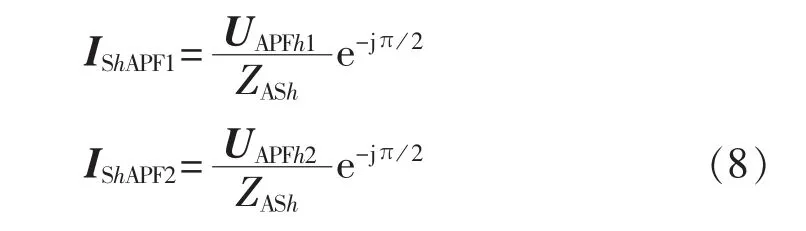
记ISh0′=ISh0+IShAPF2，则式（1）可以转化为：

比例控制信号是随着系统电流谐波的变化而变化的，调节速度快，而校正信号在一个控制周期内是不变的，其产生的APF输出电压相当于一个稳定的正弦电压源，因此ISh与ISh0′之间也满足式（6）关系，即：

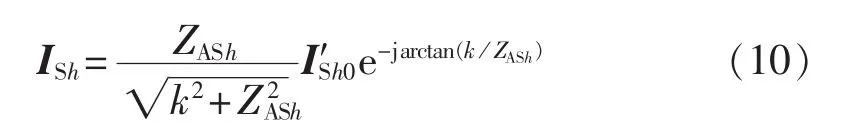
若能够以系统剩余谐波电流ISh作为反馈信号，调整校正信号使得ISh0′减小，则系统剩余谐波电流将能够进一步减小。

以APF投运时刻为0时刻，UAPFh2（i）、IShAPF2（i）和ISh（i）分别表示第i时刻的APF输出电压校正信号、由UAPFh2（i）产生的补偿谐波电流和第i时刻的系统剩余谐波电流。记ISh0′（i）=ISh0+IShAPF2（i），由于第i时刻的系统剩余谐波电流ISh（i）是第i-1时刻APF输出电压作用的结果，因此将式（10）转化成离散形式为：

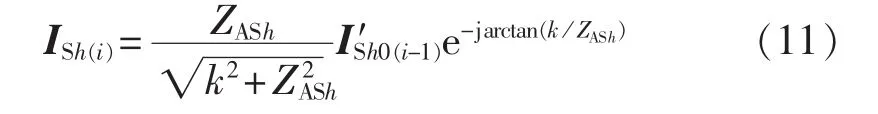
在APF投运时，令UAPFh2（0）=0，则ISh0（0）′=ISh0，利用ISh作为反馈量对UShAPF2进行调节，调节方法如式（12）所示。

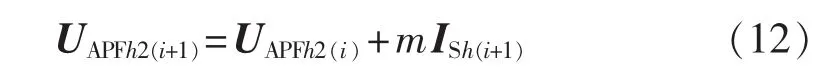
其中，校正参数m为标量常数。结合式（8）、式（11）和式（12）可得：

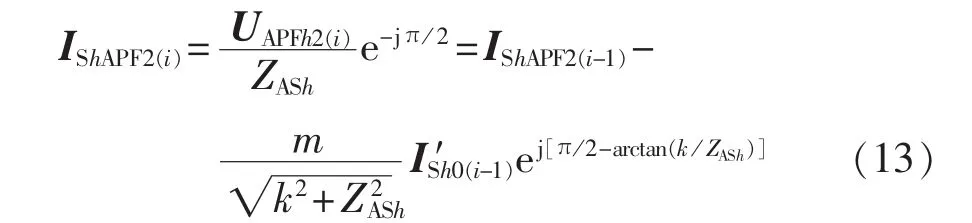
式（13）左右均加上ISh0可得：

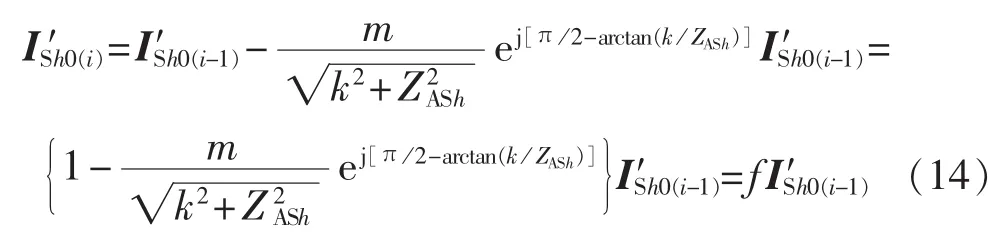
2.2 控制参数的确定

比例控制参数k和校正参数m的选择一方面要考虑滤波效果，另一方面要考虑系统的稳定性。

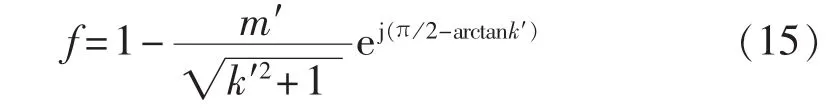
系统稳定性主要受到比例控制参数k的影响，由于时就可以实现系统剩余谐波最终趋近于0，所以在选择参数k的取值时，可首先考虑系统稳定性的要求，而不必过分强调谐波衰减倍数而使稳定裕量变小或导致失稳。比例控制作用下，系统剩余谐波电流与谐波源之间的关系如式（16）所示。

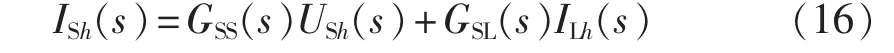
其中，GSS（s）为系统背景谐波与系统剩余谐波之间的传递函数；GSL（s）为负载谐波电流与系统剩余谐波之间的传递函数。

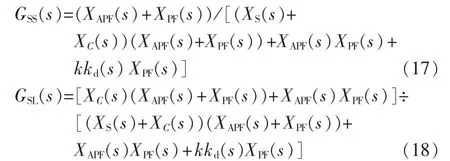
其中，kd（s）为检测和控制过程中的延时，用延时环节e-τs表示［16］。通过式（17）和式（18）的奈奎斯特图［16］可以判断取不同k值时系统的稳定性。在保证足够的系统稳定裕量的前提下，选取合适的k值，从而确定m的取值，即m＝k。

2.3 校正信号的计算

根据式（12）可以通过相量计算得出第i时刻UAPFh2（i）的幅值 Ahi和初相位 θhi的表达式如下：

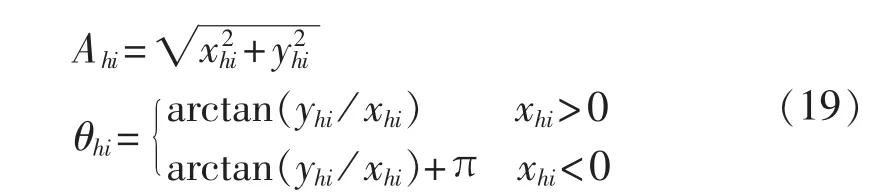
其中，xhi和 yhi如式（20）所示。

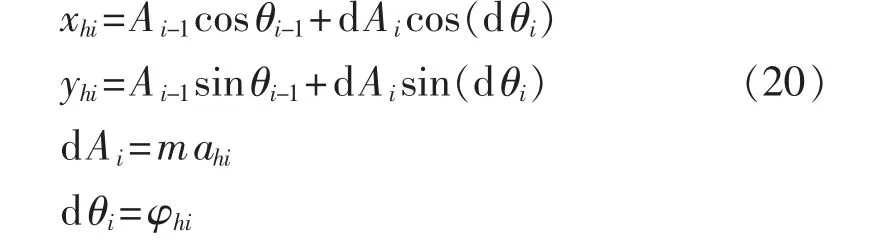
其中，ahi和φhi分别为第i时刻系统h次剩余谐波电流的幅值和初相位。

因此，APF输出电压校正信号UAPFh2的计算过程中需要检测系统剩余谐波电流的幅值和初相位，利用文献［15］提出的滑窗迭代DFT方法能够有效地检测电流中任意次谐波，且具有检测快速、计算量小的优点，该方法对系统h次剩余谐波检测的计算原理如图 4所示，图中 Sah、Sbh方程如式（21）所示，幅值和初相位计算方程分别如式（22）和式（23）所示。

图4 滑窗DFT谐波检测原理Fig.4 Principle of sliding window DFT harmonic detection

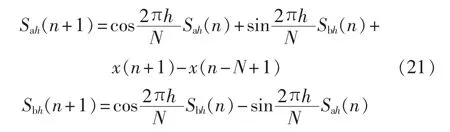
其中，N为一个工频周期电流的采样点数；Sah和Sbh为滑窗DFT的2个迭代过程量；｛x（n）｝为实时采样数据；Sah（1）=x（1）；Sbh（1）=0。

在用文献［15］提出的滑窗迭代DFT方法求出Sah和 Sbh的基础上，利用式（22）和式（23）可以计算出系统h次剩余谐波电流的幅值ah和初相位φh。需要说明的是，系统h次剩余谐波电流的幅值ah和初相位φh只需要在每个控制周期计算一次。

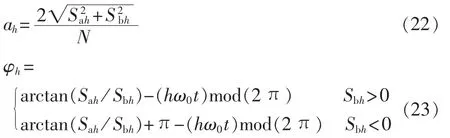
其中，mod表示取余运算；ω0为工频角速度。

因此，根据式（19）—（23）可以计算出 APF 输出电压校正信号。

2.4 控制策略框图

图5 给出了并联混合APF的控制系统框图，包括谐波控制和直流电容电压控制。

图5 并联混合APF的控制系统框图Fig.5 Block diagram of shunt hybrid APF control system

谐波控制部分包括比例控制信号的计算和校正信号的计算：比例控制信号UAPFh1通过将系统电流与基波电流相减所得谐波电流乘以k倍之后得到；APF 输出电压校正信号 UAPFh2利用式（19）—（23）计算得到。

直流电容电压控制部分的输入为电网电压US和电容电压Ud。从文献［10］可以知道APF输出的有功电流仅与APF输出电压中与电网电压相位相差π/2的分量有关，利用直流侧电压与设定值之间的差值通过PI控制器调节这一分量的大小，从而实现直流侧电压的稳定调节。

3 仿真及结果分析

从文献［15］中可知滑窗迭代DFT方法检测响应时间约为滑窗宽度，本文选择滑窗宽度为1个工频周期，因此以20 ms作为控制周期进行控制。利用PSCAD仿真软件，根据图5建立仿真模型，仿真参数：系统线电压有效值380 V，系统电感LS=0.22 mH；负载为三相整流二极管；PF调谐在4.75次谐波处，C=300 μF，LPF=1.5 mH，RPF=0.0471 Ω，品质因数为50；APF直流侧电容Cd=10000 μF，直流电压设定值为150 V，APF输出电感LAPF=1.41 mH，电阻为RAPF=0.05Ω；电流采样频率和PWM载波频率为12800Hz。

3.1 控制参数取值验证

以5次谐波为例，τ取100 μs，选择比例控制参数 k 分别为 15、25、35 和 45 时，GSS（s）和 GSL（s）的奈奎斯特图如图6所示。从图6中可看出只有k=45时系统不稳定。为了保证足够的稳定裕量，选择比例参数k=25进行仿真，同时计算得到满足的校正参数m的取值为［0，50］，因此分别取m为0、5、10、15、20、25、30、35、40、45 进行仿真，比较系统电流5次谐波有效值的变化情况，m=0表示仅加入比例控制。

图6 GSS（s）和 GSL（s）的奈奎斯特图Fig.6 Nyquist diagram of GSS（s） and GSL（s）

仿真时序为：0 s时投运 5次 PF，0.5 s时投运APF，1.5 s时负载电阻从 10 Ω 变为 5 Ω。负载为5 Ω时，负载电流波形及其频谱如图7所示，其主要谐波的含量如表1所示。

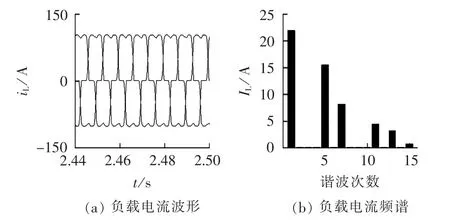
图7 负载电流波形及频谱Fig.7 Waveform and spectrum of load current

表1 负载电流主要谐波含量Table 1 Main harmonic contents of load current

系统5次剩余谐波电流有效值变化曲线如图8所示，2.5 s时系统5次谐波电流含量和滤除率如表2所示。

图8 参数m取不同值时系统5次谐波电流有效值曲线Fig.8 RMS curve of system 5th harmonic current for different m values

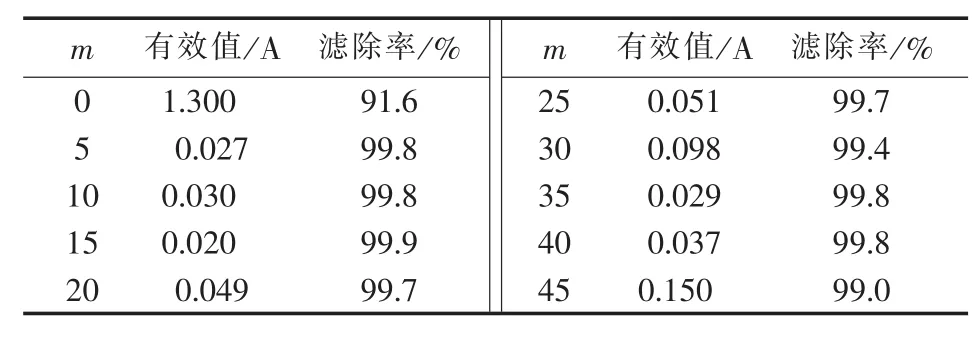
表2 系统5次谐波电流有效值及其滤除率Table 2 RMS and filtration rate of system 5th harmonic current

从图 8（b）—（i）可以看出，若 m 在［5，40］内取值，谐波发生突变时，系统谐波电流能够迅速下降，最终趋近于0，说明所提出方法具有响应快速、控制误差小的优点；从图8（j）中可以看出，当m接近于上限时，谐波曲线出现波动，充分说明了上述理论分析得到的m的取值范围是正确的。从表2中可以看出，对于 m∈［5，40］，谐波滤除率都较高，2.5 s时 APF输出电压校正信号的幅值和初相位已经收敛于一个稳定值，使得系统剩余谐波电流接近于0，体现了所提方法的有效性和正确性。基于仿真结果和理论分析，建议m取值略低于k。

3.2 对背景谐波抑制作用的验证

取m=20，分别在不加入背景谐波和加入3%的5次谐波电压、2%的7次谐波电压、1%的11次谐波电压2种情况下进行仿真。仿真时序如下：0 s时投运5次PF，0.5 s时投运APF，1.5 s时负载电阻从10 Ω 变为 5 Ω。

滤波后系统电流波形如图9所示，各次谐波含量的变化曲线如图10所示，各次谐波的含量和谐波滤除率如表3所示。从图9中可以看出有、无背景谐波2种情况下，系统电流最终的波形都接近于正弦波；加入背景谐波后，在负载发生突变时谐波减小的速度变慢，但最终都趋近于0；从表3中可看出，有、无背景谐波2种情况下，系统电流各次谐波滤除率都较高，有背景谐波时各次谐波电流的滤除率略低于无背景谐波时的谐波电流滤除率。仿真说明背景谐波会使滤波的动态效果变差，但对稳态效果影响不大。

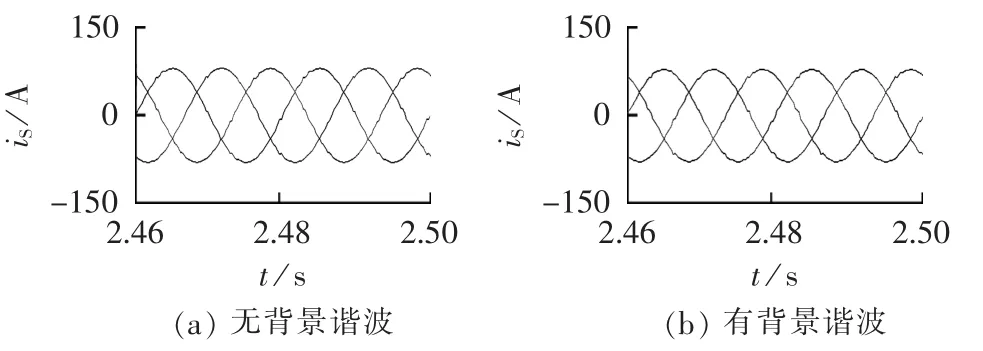
图9 系统电流波形Fig.9 Waveforms of system current

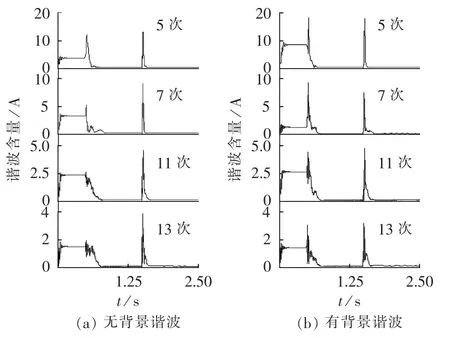
图10 背景谐波对滤波效果的影响Fig.10 Impact of background harmonic on filtering effect

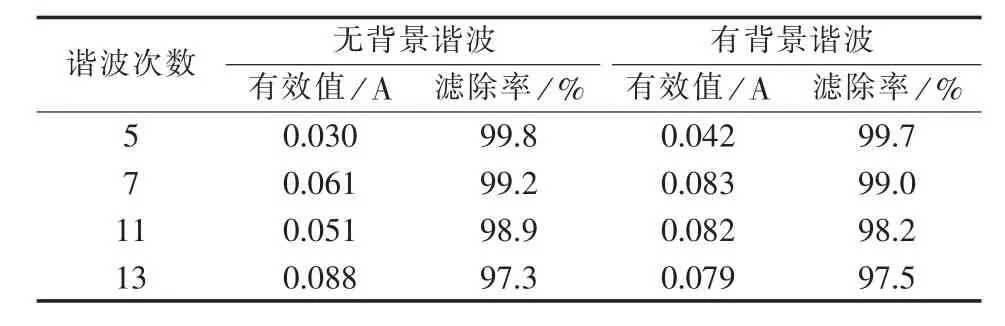
表3 系统电流各次谐波含量及其滤除率Table 3 System current harmonic content and corresponding filtration rate for different orders

实际情况中，负载变化不会太剧烈，因此仿真分析负载变化较小时的滤波情况，仿真时序为：0 s时投运5次PF，0.5 s时投运APF，1.5 s时负载电阻从10 Ω 变为 9 Ω。

滤波后系统电流波形如图11所示，各次谐波含量的变化曲线如图12所示，各次谐波的含量和谐波滤除率如表4所示。从图11中可以看出有、无背景谐波2种情况下，系统电流最终的波形都接近于正弦波；从图12中可以看出有、无背景谐波2种情况下，负载发生较小突变时，系统谐波升高的幅度较小，且在较短时间内会降低到接近于0；从表4中可以看出，有、无背景谐波时，系统电流各次谐波滤除率都较高，有背景谐波时各次谐波电流的滤除率略低于无背景谐波时的谐波电流滤除率。

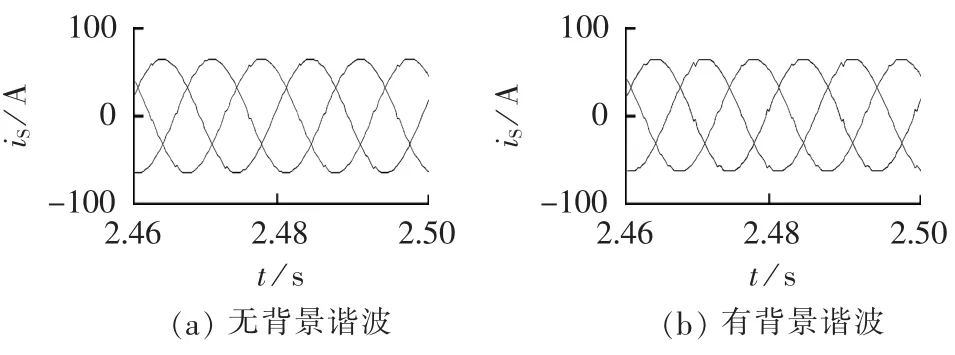
图11 系统电流波形Fig.11 Waveforms of system current

图12 背景谐波对滤波效果的影响Fig.12 Impact of background harmonic on filtering effect

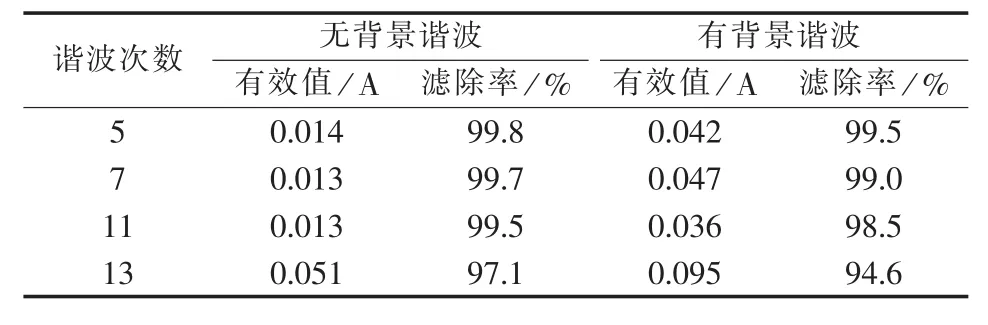
表4 系统各次谐波含量及其滤除率Table 4 System current harmonic content and corresponding filtration rate for different orders

3.3 动态效果改善

负载发生剧烈变化时的滤波动态效果主要体现在谐波电流有效值下降的速度和谐波电流上升的最高值。

从图10中可以看出，负载发生剧烈变化时，各次系统谐波有效值均突然上升，但都会在30 ms左右下降到较小值，如5次谐波有效值最高上升到18 A，30 ms内下降到2 A；7次谐波在30 ms内下降到约1 A，11次谐波在30 ms内下降到0.8 A，13次谐波在30 ms内下降到0.8 A。因此，谐波电流有效值的下降速度较快。

负载发生剧烈变化时各次系统谐波有效值突然上升是不可避免的，其中5次谐波有效值上升最高，影响动态滤波效果，一方面是因为负载5次谐波含量较高，另一方面是因为APF输出电感和混合APF无源部分结合等效于一个调谐次数大于5次的PF，造成系统5次谐波对负载电流的变化很敏感。在公共连接点（PCC）并联一个5次PF可以为负载电流中的5次谐波提供低阻抗通路，减小系统5次谐波对负载电流的变化的敏感程度，同时也能一定程度上改善7、11、13次谐波的滤波效果，从而改善负载动态变化频繁、剧烈场合的应用效果。PCC并联一个5次PF后系统的拓扑如图13所示。

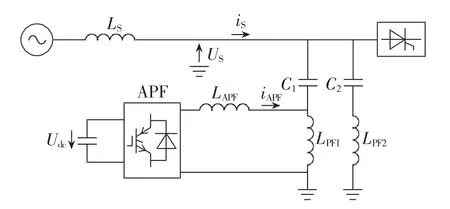
图13 改进的混合APF系统结构Fig.13 Structure of advanced hybrid APF system

根据图 13 进行仿真，取 C1=300 μF，C2=100 μF，2组PF均调谐在4.75次谐波处，品质因数为50，其他条件不变，分别在有背景谐波和无背景谐波下仿真，仿真时序为：0 s时投运5次PF，0.5 s时投运 APF，1.5 s时负载电阻从10 Ω变为5 Ω。仿真结果如图14和图15所示。

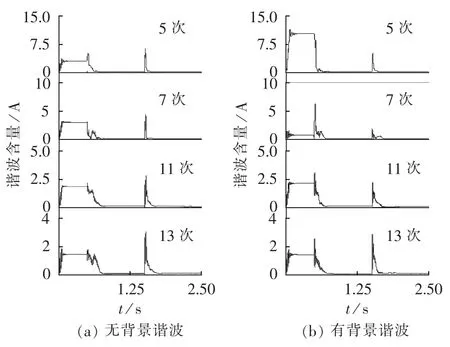
图14 并联5次PF后的滤波效果Fig.14 Filtering effect，with parallel 5th PF

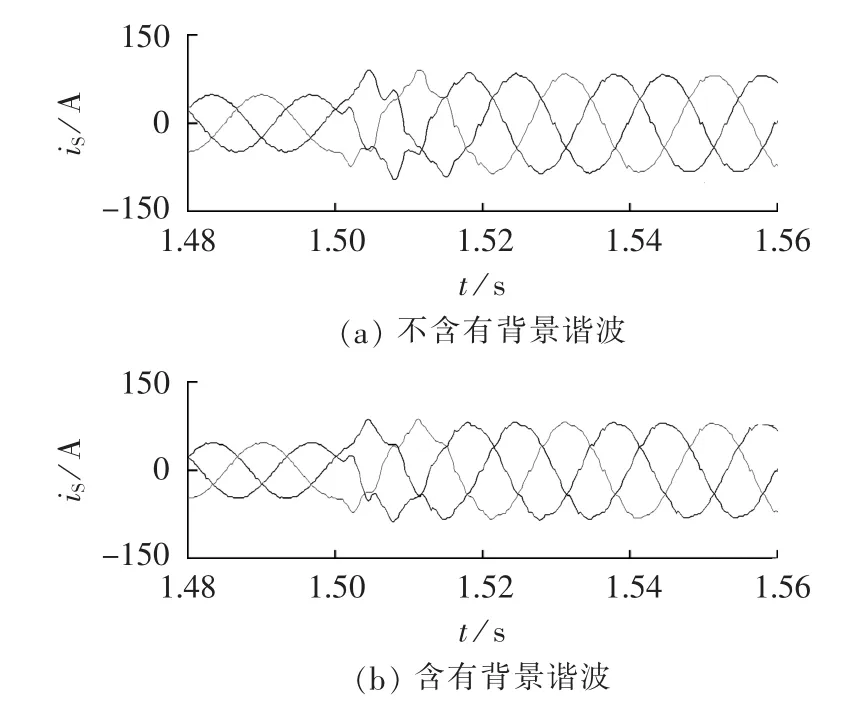
图15 负载突变期间系统电流时域波形Fig.15 Time-domain waveform of system current during sudden change of load

对比图10和图14可以看出并联5次PF后，负载发生剧烈突变时，系统5次谐波电流有效值上升的最大值由原来的18 A变为6 A，7次谐波电流上升的最大值由原来的8 A变为5 A左右，11和13次谐波电流的滤波效果在并联5次PF后也有一定的改善，说明并联5次PF能够改善负载发生剧烈突变时整体的动态滤波效果。因此建议在负载变化剧烈、频繁的场合，并联一组5次PF。

需要说明的是，在含有背景谐波的情况下，APF接入时系统7次谐波电流突然升高到较大值，是因为APF输出电感和PF1构成接近7次的PF，在系统7次背景谐波的作用下产生较大的7次谐波电流。但是APF稳定工作后，不会再出现7次谐波较大的情况。

图15 给出了负载发生突变期间系统电流的时域仿真波形，从波形中可以看出系统电流波形仅在短暂时间内畸变，负载发生突变1个工频周期后系统电流波形就接近于正弦波形。

4 结论

本文提出了一种基于输出电压校正的混合APF控制策略，在比例控制的基础上，给APF输出电压一个确定幅值、相位的正弦校正信号，达到滤除谐波的目的。给出了控制策略的参数确定方法以及校正信号幅值相位的计算方法，通过并联5次PF改善了负载剧烈变化时的动态滤波效果。仿真结果表明，所提出的方法参数选择简单有效，在负载变化时和系统含有背景谐波的情况下都有较好的动态特性和滤波效果。