单部件劣化系统的维修成本优化研究
(中南大学商学院 湖南长沙410083)
一、引言
随着技术的进步,设备变得越来越复杂化,企业花费在设备维修上的成本占企业运营成本的比例也变得越来越大。从单台设备的生命周期成本角度来看,维修成本是全生命周期成本的重要组成部分。因此,优化维修成本对降低企业运营成本、提高企业竞争力和全生命周期成本的优化有很大贡献。
目前检测到系统的状态变得越来越容易和可信,从而视情维修逐渐成为研究的热点。视情维修是通过对设备进行定期或序贯的或连续的检测来获知系统状态,进而安排维修工作以避免产品失效。系统劣化过程是一个随机过程,对于单调和逐渐劣化的随机过程,用Gamma过程描述是最合适的。Gamma过程具有很好的数学特性,是一个具有独立、非负增量的随机过程。Abdel-Hameed提出用Gamma过程作为描述系统发生随机劣化的适当模型,称为 “Gamma磨损过程”。Park、Kong和 Park以 Gamma过程描述系统的劣化过程,以维修费用率最小为目标,建立了检测周期固定的视情维修模型,用解析法求得最优预防维修状态阈值。程志君进一步考虑维修延迟,以系统的平均费用率最低为目标,联合优化检测间隔期和预防维修阈值。李玲等将Gamma过程与几何过程相结合,提出一种加速劣化模型,以系统平均费用率最小为目标,求解最优视情维修策略。Huynha et al.考虑系统的劣化和创伤性事件两种竞争失效模式,以维修费用率最小为目标,建立视情维修的定期检测/更换模型,得到最佳检测间隔期和预防维修阈值。在目前视情维修的研究中,在以维修成本最低为目标时,很少考虑维修时间且没有考虑维修期间内的生产损失。
本文针对连续劣化单部件系统,考虑实际中普遍采用的定期检测,建立了以系统平均维修成本率最低为优化目标,以检测间隔期和预防维修阈值为变量的维修优化模型。在模型中,假设预防维修时间和故障后维修时间服从一般分布,考虑检测成本、预防维修成本、故障后维修成本、维修期间的生产损失和维修延迟的停机损失。
二、模型建立
(一)模型假设与分析
1.将连续两次更新系统至全新状态的期间定为一个周期。
2.用随机变量 X(t)表示系统在时刻 t的劣化状态,若无维修行为,X(t)是连续且单调递增的。当t=0时,X(t)=0,表示系统处于全新工作状态。随机变量 X(0),X(1)-X(0),… ,X(t)-X(t-1)是非负、平稳和相互独立的。
3.对系统采取视情维修策略,在一个周期内进行定期检测,检测间隔期为 T,检测时刻 tk=kT(k=0,1,2…),每次检测成本为Ci,检测时间忽略。
4.当系统状态超过预防维修阈值时,进行预防维修;系统发生劣化故障时,进行故障后维修,均修复如新。其中预防维修时间服从均值为βp的一般分布,故障后维修时间服从均值为βc的一般分布;预防维修成本为Cp,故障后维修成本为Cc,均不包括生产损失。 其中 Ci≤Cp≤Cc,βp≤βc。
5.系统劣化故障需要检测确定,如果发生劣化故障,直至下次检测前系统是失效的,这时单位时间内失效停机的生产损失为Cd。
6.系统维修优化的目标是系统的平均维修成本率最低。
系统存在两个状态阈值L和M,L是劣化故障阈值,一般由制造商给定,M是预防维修阈值。对系统状态进行定期检测,在第k个检测时刻tk检查到的系统状态是 X(tk)。 若 X(tk) 如果预防维修阈值M设置得过低,会使预防维修工作增多,可能造成维修过剩,增加维修成本;设置的过高,可能导致维修不足,发生劣化故障的概率增加,从经济性和安全性来看,都是不应该发生的。同样,检测间隔期设置不当也会造成维修不足或维修过剩。因此,要使平均维修成本率最低,就要找到最优的预防维修阈值M*、定期检测间隔期T*。 图1 系统周期示意图 本文用Gamma过程来描述两次维修行为之间的系统劣化过程。假设连续时间随机过程 {X(t),t≥0}是平稳Gamma过程,则在时刻t劣化水平的概率密度函数是形状参数为αt、尺度参数为β的Gamma密度函数。 Gamma过程是一个非减的连续时间随机过程,随α和β的不同,可以描述系统不同的劣化特征。平均劣化率为 α/β,方差为 α/β2。 设τx表示系统从全新状态到达状态X的时间,则τx的分布函数计算如公式(2)所示: 其概率密度函数为: 由更新定理可知:系统平均维修成本率可以看作在一个周期Γ内的维修成本率,因此系统平均维修成本率C(T,M)可表示为公式(4)。 假设系统在一个周期内检测Nk次后更换,则一个周期的平均长度E[Γ]和平均维修成本E[C]的计算如公式(5)、(6)所示。 其中:Pp是系统在一个周期内发生预防维修的概率,Pc是系统在一个周期内发生故障后维修的概率,βp是预防维修时间的期望,βc是故障后维修时间的期望,P{Nk=k}表示系统在第k次检测时更换的概率,E[Nk]是系统在一个周期内检测次数的期望值,E[d]是系统在一个周期内维修延迟的平均时间。 由公式(4)、(5)和(6)可得到系统平均维修成本率C(T,M),可表示为公式(7): 要找到最优的预防维修阈值M*、定期检测间隔期T*,使系统平均维修成本率C(T,M)最小,建立维修优化方程如公式(8)所示: 由相关的数学知识可知,一个周期内检测次数的期望值E[Nk]如公式(9)所示: 其中,检测k次的概率P{Nk=k}的计算如公式(10): 系统更新可能是由预防维修也可能是由故障后维修引起的,发生预防维修的概率Pp和发生故障后维修的概率 Pc的计算如公式 (11)、(12)所示: 假设系统在两次检测之间的时刻t失效,即(k-1)T<t<kT,则有系统在一个周期内维修延迟的平均时间E[d],计算如公式(13): 将公式(9)至公式(13)代入维修优化方程(8),可得到系统的平均维修成本率 C(T,M)与决策变量(T,M)之间的关系。 参数(α,β)可以通过对系统劣化数据的分析,利用数理统计方法和参数估计得到。在此,假设系统劣化过程服从参数是α=1、β=1的Gamma过程。设定系统的劣化故障阈值L=10,检测费用Ci=1,预防维修成本Cp=10,故障后维修成本Cc=40,维修延迟的单位时间损失Cd=10,预防维修时间的期望βp=0.5,故障后维修时间的期望 βc=1。 表1 不同检测间隔T下的最优预防维修阈值M和平均维修成本率C(T,M) 为使系统的平均维修成本率最低,要找到最优维修策略(T*,M*)。 由于函数 C(T,M)的复杂性,结合实际,对检测间隔期T采用离散值,寻求最优解。首先根据经验得到T的取值范围和增加幅度△T;然后考虑预防维修阈值的约束条件0 将假设的模型参数值代入模型,采用上述算法,取最小检测间隔为1,最大检测间隔为10,考虑实际情况,置增加幅度△T=1。通过Matlab编程计算可得到表1的结果,由表1可观察到最优的维修策略(T*,M*) =(2,5.9994),此时,C(T*,M*)=2.8273。 本文通过寻求最佳维修策略,从定量的角度来优化维修成本。对于连续劣化单部件系统,以Gamma过程描述其劣化过程,假设预防维修时间和故障后维修时间服从一般分布,考虑设备维修过程中的检测成本、维修成本以及由于维修和维修延迟引起的生产损失,在此基础上,以系统的平均维修成本率最低为优化目标,以检测间隔期和预防维修阈值为决策变量,建立了维修优化模型。算例分析证明了模型的可行性。通过该模型,可以找到最优的检测间隔期和预防维修阈值,使系统的平均维修成本率最低,对企业维修成本优化的决策有一定的参考作用。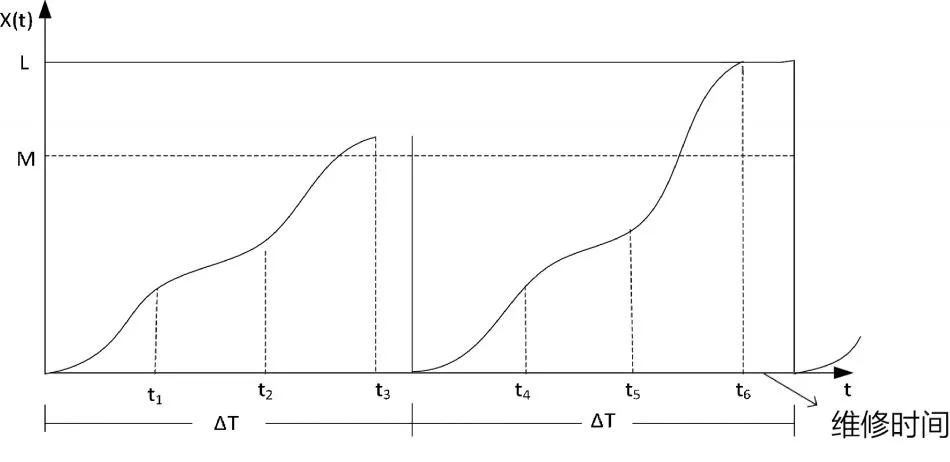
(二)劣化过程
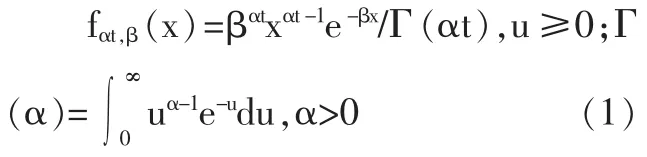

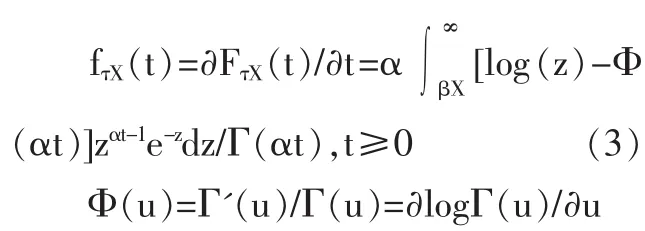
(三)建立系统平均维修成本率模型
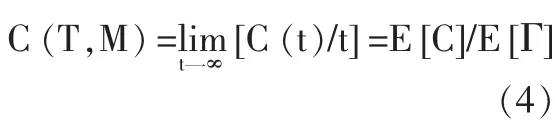
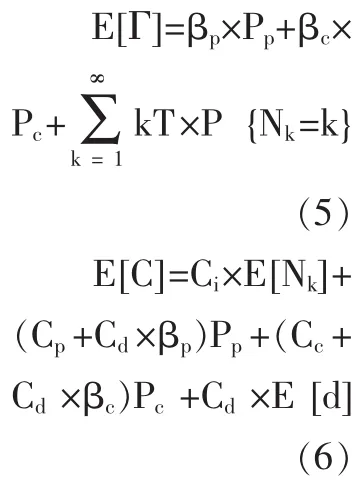
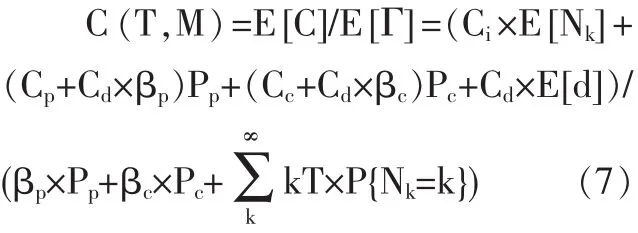
(四)维修优化模型
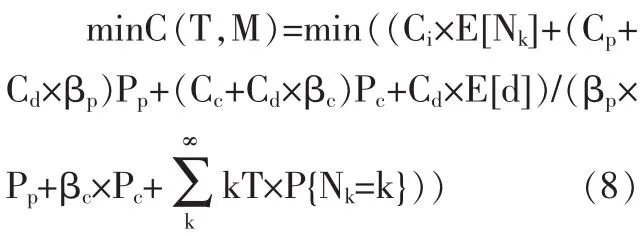
三、模型分析与求解
(一)一个周期内检测次数的期望值



(二)概率 Pp、Pc
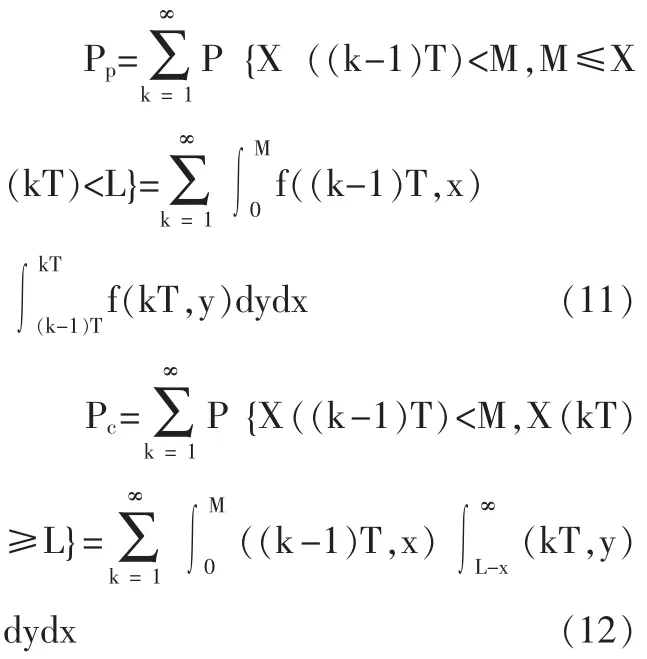
(三)维修延迟的平均时间

四、算例分析

五、结论

