Y/△接线变压器三角形侧环流计算新方法

凌 光，姚文熙

（1.国网绍兴供电公司，浙江 绍兴 312000；2.浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

Y/△接线变压器广泛应用于各电压等级的变电站中，220 kV及以下电压等级多采用三相一体式结构。△侧不能配置绕组电流互感器（TA），因而无法直接获取绕组电流。在计算差流时，只能通过相位补偿来避免产生不平衡电流。目前常用的补偿方式有种。但无论采用何种补偿方式，由于△侧绕组环流的影响，都不能准确计算等效瞬时电感值［1-4］，使得基于此的励磁涌流判据失效，不能准确区分空载合闸和主变故障2种状态，增加了差动保护误动概率［5-9］。

当前已有不少论文提出了计算△侧绕组环流的方法。文献［10-11］根据变压器回路方程，给出Y/△接线变压器环流计算的方法，但需要知道变压器参数。文献［12］提出了一种基于数值积分求得变压器参数、再进一步求取环流的方法，在处理过程中用到了△侧电压；但电压互感器一般装设在母线上，在变压器空投时是无法获取△侧电压数值的。文献［13-14］根据零序电流和环流的比例关系，通过求取比例系数来得到环流，但需要控制合闸角或者较长的计算时间，现场应用困难。

本文根据Y/△接线变压器等效电路的微分方程计算环流，得出△侧环流和Y侧零序电流的比例关系。通过分析三相合闸电流和零序电流的波形特征，确定磁通未饱和部分，得到零序电流和环流的比例系数，从而求得△侧绕组环流。该方法对合闸角无特殊要求，也不需要知道变压器参数，而且在一个工频周期内就能计算出环流，因此能准确计算差流。该方法的应用，有利于差动保护快速准确动作，并有效拓宽了基于等效瞬时电感的励磁涌流判据的应用范围。

1 三角形侧环流计算

Y/△接线变压器等效电路如图1所示。把△侧电压电流换算到Y侧，得到如图2所示的单相等效电路。根据等效电路，从Y侧和△侧分别计算励磁绕组两端电压，设三相电源对称，变压器两侧三相绕组各自对称，得到电压方程。

图1 Y/△接线变压器接线图Fig.1 Wiring diagram of transformer with Y/△ connection

图2 变压器单相等效电路Fig.2 Single-phase equivalent circuit of transformer

其中，RS和LS分别为电源的等效电阻和电感；R1和L1分别为变压器Y侧的各相绕组电阻和漏电感；R2和L2分别为△侧的各相绕组电阻和漏电感。△侧绕组电流可以分解成两部分：一部分提供△侧线电流，三者相加等于0；另一部分等于环流iD，三者相加为3倍环流3iD。假设三相电源对称，则EA+EB+EC=0，而△侧3个线电压之和亦为0，即uab+ubc+uca=0，把方程（1）中3个式子左右两侧相加，整理后得到方程：

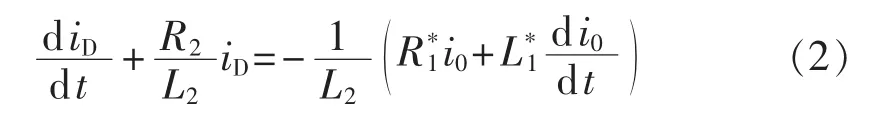
其中

求解上述微分方程，考虑到空载合闸的初始条件iD=i0=0，可以求得环流iD的解析表达式为：

设信号采样周期为ΔT，将式（3）离散化，经过ns个采样周期后，环流应为：

在已知变压器及系统参数，或者根据在线监测获取参数［15］时，可以根据上式准确计算环流，进而求取差流，来判别励磁涌流。若参数难以获取，忽略电阻，令则式（4）可以进一步简化为：

△侧绕组环流和Y侧零序电流成比例，后者根据高压侧电流可以计算得到。因此只要求得比例系数，就可以求取环流。

2 Y侧零序电流和△侧环流比例系数计算

当空载合闸时，由于△侧线电流为0，各相绕组电流就等于环流，即ia=ib=ic=iD。由图2可知，两侧同一相绕组电流的关系是iA=ia+im。当磁通不饱和时，励磁电流im可忽略，于是就有iA=ia，即环流和Y侧电流相等。再通过自产得到该区域Y侧的零序电流，就可以求出两者的比例系数。由于比例系数只跟变压器和系统参数有关，在空载合闸至励磁涌流消失这段较短的时间里，可以认为是不变的，因而在磁通非饱和区求得的比例系数同样适用于磁通饱和区。

根据以上分析，只要确定磁通非饱和区域，就可以根据该区域内的Y侧电流求得比例系数，进而求出环流。在这一区域内，Y侧对应相电流和零序电流成比例关系。文献［13］指出，波形相关度技术可以用来研究2组离散信号x和y的相关程度，用相关系数 ρ表示。设一段时间内采样点数为N，则ρ的表达式为：

当两信号相同或成比例时，ρ的绝对值为1，否则小于1。两信号的相关程度越大，其绝对值越接近于1。在磁通非饱和区域内，对应相电流和零序电流成负比例，其相关系数应该很接近于-1。所以选择合适的窗口长度，计算相电流和零序电流的相关系数，就可以识别非饱和区。本文采用1/4工频周期作为窗口长度，与文献［13］所不同的是，本文不需要控制合闸角，取三相电流分别与零序电流进行相关度计算。只要有一相的非饱和区长度大于窗口长度，就可以求得比例系数。

实际上，在空载合闸于正常系统的情况下，若剩磁大小不超过额定磁通幅值，则三相电流中至少有一相存在1/3周期长度位于磁通非饱和区，这个结论可以得到严格证明。若电源电压为umsin（ωt+α），不考虑电阻影响，则磁通可表示为：

其中，Φm为额定磁通幅值；Φs为剩磁。当磁通大小不超过幅值Φm时，磁通位于非饱和区，满足：

把式（7）代入式（8）并记 β=Φs/Φm（-1≤β≤1），可以得到：

记上式中cos（ωt+α）的上、下限分别为m和n，而余弦值本身的取值区间是［-1，1］，所以 cos（ωt+α）的取值为［n，m］和［-1，1］的交集，如图3中的阴影部分所示。

图3 cos（ωt+α）的取值区间Fig.3 Range ofcos（ωt+α）

由于三相合闸角互差120°，设A相合闸角为α，则B、C相合闸角为α±120°。分析这3个余弦值的绝对值，不难证明最小值总是不超过1/2，即：

因此 cos（ωt+α）的取值区间应包含［1/2，1］，即：

上式ωt的解区间长度为2π/3，为1/3工频周期。 当 cos α＋β＜0 时，应有 cos α＋β≥-3 /2，所以上限 m=1+cos α＋β≥-1/2，因而下式成立：

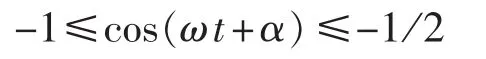
ωt的解区间长度同样为2π/3，所以磁通非饱和区间的长度至少为1/3工频周期。在极个别情况下，剩磁可能超过最大额定磁通，导致非饱和区长度减少。因而取1/4工频周期作为窗口长度，可以保证至少有一相的磁通非饱和区长度大于该数据窗口。

设窗口长度为N，理论上磁通非饱和区对应相电流和零序电流的相关系数ρ应为-1，考虑到零序电流和环流并不是精确的比例关系，取ρ＜-0.99作为判据，并把该段数据记为有效数据，用于计算比例系数。为防止电流过零附近分母过小，使得比例系数误差增大，Y侧相电流和零序电流均取满足条件所有数据的绝对值和，再求比例系数。若满足条件的数据三相都存在，则取数据长度最长的一相，计算得到的比例系数作为最终结果，算法流程图如图4所示。

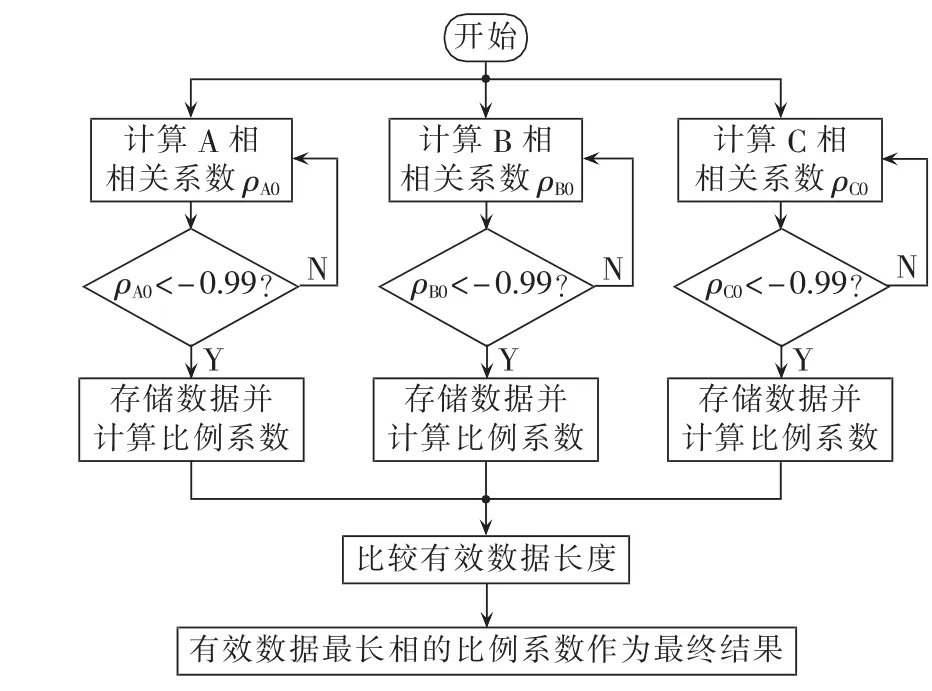
图4 比例系数计算流程图Fig.4 Flowchart of correlative coefficient calculation

设有效数据的起始序号为p，数据长度为x，并假设计算相别为A，那么比例系数k的计算式可记作：

求得比例系数后，就可以根据Y侧零序电流求得△侧环流，最终准确求取差流，从而判断差动保护是否应动作。当变压器空载合闸以及轻微匝间故障时，差动保护反应不灵敏，此时差流的准确计算显得尤为重要。而当Y侧发生接地故障时，相当于电源出口处直接短路，短路电流较大，差动保护能灵敏反应。如图5所示，假设A相接地，图中也给出了TA的位置。

图5 变压器Y侧接地Fig.5 Grounding at Y side of transformer

此时若要计算△侧环流，则要准确获知Y侧的零序电流；但由于接地电流iF的存在，已经不能通过3个相电流TA计算得到，但可通过中性点TA获取零序电流3i0。实际上，此时已无进一步计算环流的必要，因为系统的零序差流已经可以准确获取：

该差流值与△侧绕组无关，与励磁涌流无关，变压器零序差动保护将灵敏动作，切除故障。即使不采用中性点电流3i0，由于故障电流较大，利用或方式补偿计算差流，也能对接地故障有非常灵敏的反应能力，在第一时间出口跳闸。

3 仿真分析

利用MATLAB的Simulink模块建立如图6所示的仿真模型，以验证本文所提出的环流计算方法。Y，d11接线变压器采用三相一体式结构，电压等级为110 kV/35 kV，容量为250 MV·A。Y侧绕组电阻和电感分别是0.002 p.u.和0.08 p.u.，△侧绕组电阻和电感分别是0.002 p.u.和0.08 p.u.，铁芯饱和特性为［0 0；0.0154 1.2；1 1.2613］，仿真频率为 2.5 kHz。

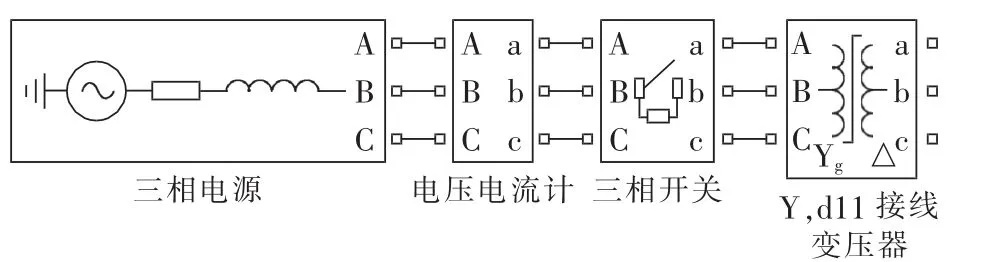
图6 变压器仿真模型Fig.6 Simulation model of transformer

合闸角随机选择，利用式（5）计算空载合闸时△侧的环流，和实际环流进行对比，如图7所示，发现按此式计算得到的环流与实际环流十分吻合，由此证明了式（5）的合理性。

图7 计算环流和实际环流Fig.7 Calculated and real circulating currents

上述仿真结果证明了在空载合闸过程中，参数已知时△侧绕组环流可以准确求取；在更多不知道参数的场合，需要通过文中提出的方法来求取环流。再次进行空载合闸试验，合闸初相角和剩磁随机产生，得到三相电流和环流如图8所示。

图8 三相电流与环流Fig.8 Three phase currents and circulating current

分别计算各相电流和零序电流的相关系数，结果如图9所示，ρA0、ρB0、ρC0分别为 A、B、C 相和零序电流的相关系数。共计算了2个工频周期的数据，相关系数分布一致，所以取1个周期的数据即可完成计算。

图9 三相电流与零序电流相关系数Fig.9 Correlation coefficient of phase current with zero-sequence current for three phases

由图9可知，B相电流的第31～45号采样点所对应的相关系数计算值为-1，如图中虚线框所示。包含计算窗口内的10个采样点，共存在24个采样点对应非磁通饱和区（第22～45号采样点）。根据这24个采样点的电流以及零序电流值，根据式（9）求得比例系数为1.53，按式（5）计算环流，得到计算环流和实际环流，对比如图10所示。

由图10可知，计算环流和实际环流基本吻合，验证了文中提出算法的可靠性。考虑最不利情况，剩磁为100%额定最大磁通，A相合闸角为0°。而且B、C相剩磁为负方向，A相剩磁为正向，进行空载合闸仿真，得到高压侧三相电流和环流，再分别计算各相电流和零序电流的相关系数，结果如图11所示。

图10 剩磁随机时的实际环流与计算环流Fig.10 Calculated and real circulating currents when residual magnetism is random

图11 高剩磁时的相关系数Fig.11 Correlation coefficient when residual magnetism is high

可以发现仍然存在大于数据窗口的区域，在此区域内零序电流和相电流成比例，B相虚线框部分即为符合要求数据。根据文中提出算法计算环流，并与实际环流对比如图12所示，两者基本吻合。

图12 高剩磁时的实际环流与计算环流Fig.12 Calculated and real circulating currents when residual magnetism is high

当变压器空载合闸于匝间故障时，故障相零序电流和环流的比例关系将不成立，但非故障相的比例关系依然成立，仍可以依此计算环流。当匝间故障时，非故障相因为二次负载阻抗变小，磁通更不容易饱和，所以存在更多的有效数据可以用于计算环流。而当三相都不存在有效数据时，说明变压器发生了两相甚至三相短路，这也可以作为保护动作跳闸的一个辅助判据。设A相发生5%匝间故障，把仿真得到的各相电流和零序电流分别计算相关系数，结果如图13所示。由图13可知，B相和C相均存在较大区域数据，和零序电流成比例。针对本次故障，取B相电流第10～40号数据点以及对应的零序电流计算比例系数，并根据算得的系数求得环流，和实际环流相比较，如图14所示。

图13 A相匝间故障时的相关系数Fig.13 Correlation coefficient when inter-turn fault occurs in phase A

图14 匝间故障时的实际环流和计算环流Fig.14 Calculated and real circulating currents when inter-turn fault occurs

由图14可知，计算环流和实际环流基本吻合，所以本算法在变压器内部故障时仍然可以适用，准确求取差流，提高差动保护动作准确率，同时也弥补了差动保护在匝间故障时反应不灵敏的缺点。

4 结语

本文提出了计算Y/△接线变压器△侧绕组环流的一种新方法。先根据变压器等效电路微分方程，推导出△侧绕组环流与Y侧零序电流成比例关系。再从理论上证明了对于任意合闸角，每个周期里至少有一相电流的磁通非饱和区不短于1/3周期。根据这一结论，结合波形相关度理论，识别出磁通非饱和区。然后利用这一区域内的电流数据求得比例系数，进而由零序电流求得空载合闸环流。最后通过MATLAB仿真验证了该方法的准确性。该方法无需已知变压器参数，无需控制合闸角，而且在一个工频周期内即可完成判断，符合现场实际情况和快速动作的要求，具有良好的应用前景。