基于反馈线性化的直流微电网全局稳定方法
杨忠林,查晓明,孙建军,刘 飞
(武汉大学 电气工程学院,湖北 武汉 430072)
0 引言
鉴于一次性化石能源消耗殆尽及生态环境日益恶化,越来越多的国家鼓励发展分布式的清洁可再生能源,如太阳能电池、燃料电池、风力机和小型燃气轮机热电联产等。分布式发电对环境污染少,能就地消化电力,节省输变电投资和费用;但分布式电源单机接入成本高、控制困难,相对大电网是一个不可控源,对电力系统的稳定性有负面影响,限制了其效能的充分发挥。为协调大电网与分布式发电间的矛盾,充分挖掘分布式发电为电网和用户带来的价值和效益,采用微电网形式将分布式电源并入大电网是较为有效的途径[1-4]。根据母线电压的不同,微电网可分为直流微电网和交流微电网。相对于交流微电网,直流微电网具有效率高、控制简单、可靠性高及电能品质好等优点,逐步受到广泛关注[5-9]。但直流微电网中含大量电力电子装置,其特性表现为恒功率负载,可能引起直流微电网母线电压不稳定[10-12]。
目前对直流微电网稳定性的研究文献报道并不多。文献[7]分析了直流级联电力电子系统的稳定条件,并总结了提高直流微电网稳定性的措施。文献[8]把直流微电网看成一个整体,通过增加有源阻尼信号改变大电网接口变换器的等效阻抗,进而提高直流微电网稳定性。而文献[13]提出在负荷点变换器中引入虚拟电容进而提高系统稳定性的方法。以上文献在建立直流微电网的模型时都未考虑微电网中电缆阻抗对稳定性的影响。文献[2]建立了含有电缆阻抗的直流微电网的简化模型,提出了直流微电网稳定的充分条件,但并没有提出改进微电网稳定性的措施。本文应用Lyapunov稳定性理论,通过反馈线性化,克服了直流微电网中恒功率负载的非线性,进而确保了直流微电网的全局稳定。
1 直流微电网的系统模型

图1 直流微电网结构Fig.1 Structure of DC microgrid
典型的直流微电网结构如图1所示[14],其中包含大量的电力电子变换器。源侧AC/DC变换器将直流微电网与大电网连接,稳定微电网母线电压,相当于直流微电网的恒定电压源。而各种发电、储能以及负荷单元也都通过变换器与直流微电网相连。当负荷点变换器工作于恒压模式并且控制性能良好的时候,负荷点变换器及其负载相对于直流微电网为恒功率负载[15-17]。
为分析简便,本文考虑直流微电网的简化模型如图2所示。
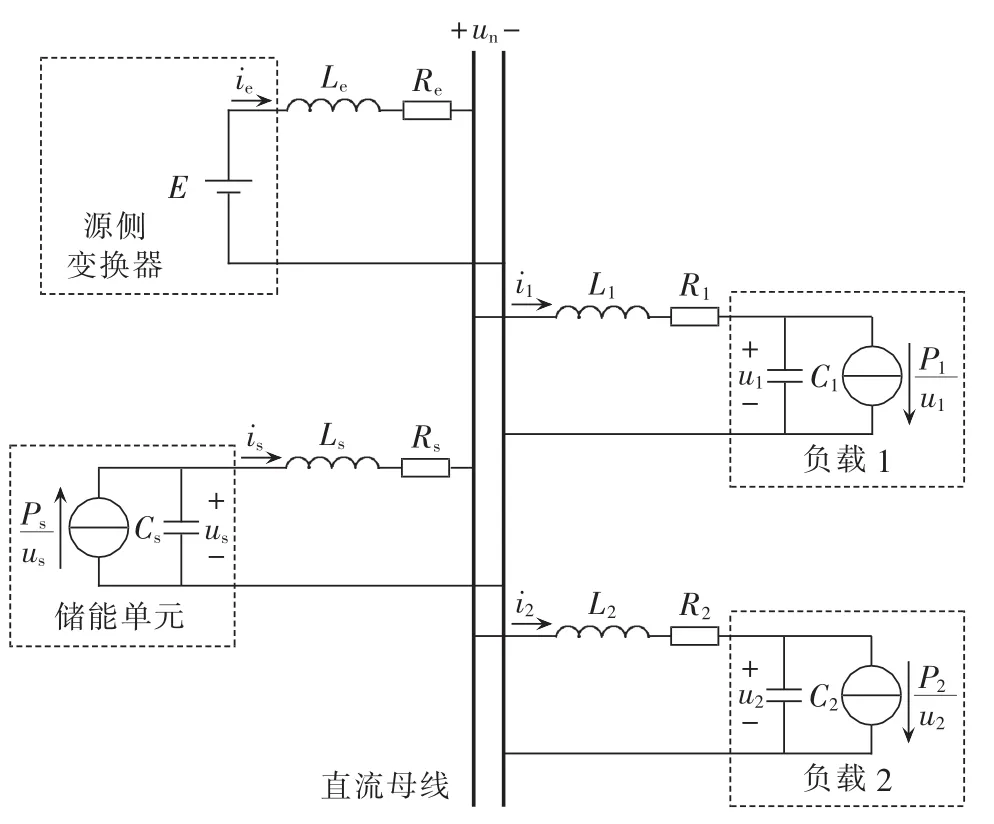
图2 直流微电网的简化模型Fig.2 Simplified model of DC microgrid
该微电网包含2个恒功率负载和1个储能单元,并通过源侧变换器与大电网相连。储能单元采用恒功率控制。由于负载单元、储能单元和源侧变换器并不能总是放置于同一地点,它们之间需要通过长电缆连接,因此必须考虑电缆阻抗对系统稳定性的影响。Le和Re分别为源侧变换器输出电缆的电感和电阻,Ls和Rs分别为储能单元输出电缆的电感和电阻,L1和L2及R1和R2分别为负载输入电缆的电感和电阻,Cs、C1和C2分别为相应变换器的滤波电容,un为直流母线电压。
2 系统的小信号稳定分析
根据电路结构,列写电路方程,可得:

选取 ie、is、i1、us、u1、u2为系统的状态变量,对式(1)整理可得:

系统的平衡点满足以下方程:
其中,U、I为前述相应u、i在平衡点处的稳态值。
对式(2)在其平衡点处进行小信号线性化得:

当系统电路参数及储能单元的输出功率Ps已经确定时,可计算得出系统的特征值,进而判断出系统是否稳定:当A的所有特征值的实部均小于零时,则该平衡点为稳定的平衡点。设系统电路参数如下:E=400 V,Le=17.3 mH,Re=0.4 Ω,Ps=1 000 W,Cs=500 μF,Ls=8.3 mH,Rs=0.2 Ω,L1=40 mH,R1=0.8 Ω,C1=800 μF,L2=19.6 mH,R2=0.42 Ω,C2=1 000 μF。可得系统的稳定区域如图3所示。
如图3所示,当恒功率负载的功率P1和P2较小时,系统是稳定的,但随着恒功率负载的功率逐渐增大,系统就有可能变得不稳定。由此可见,系统的不稳定因素主要是由负载的恒功率特性引起的。

图3 系统的小信号稳定区域Fig.3 Small-signal stable area of system
当储能单元的输出功率改变时,系统的稳定区域随着改变。如图4所示,Ps>0表示储能单元向微电网输出功率;Ps<0表示储能单元从微电网吸收功率。随着储能系统输出功率的增大,系统的稳定区域也增大,储能单元起到增加系统稳定性的功能。

图4 稳定边界随储能单元输出功率的变化Fig.4 Border of stable area for different output powers of energy storage unit
3 基于反馈线性化的直流微电网全局稳定方法
由前面分析可知,随着恒功率负载的功率增大,系统有可能变得不稳定。为了在不改变系统参数的情况下,增大系统的稳定区域,避免出现不稳定的风险,给系统增加一个全局稳定模块是一个很好的解决方法。系统的控制图如图5所示。整个系统的控制分为2层:第一层为变换器的本地控制,维持变换器输出电压的稳定;第二层为全局稳定控制,产生变换器的稳定控制信号P1stab、P2stab及Psstab,这些稳定控制信号仅在系统暂态时具有较大数值,而并不改变系统的平衡点,这将在后面的仿真实验中得到验证。稳定控制信号与系统稳态功率叠加,经变换后得到各个变换的输出电压参考电压。

图5 系统控制图Fig.5 Schematic diagram of system control
为了克服恒功率负载的非线性特性,并保证系统稳定,本文方法将进行非线性反馈,产生稳定控制信号P1stab、P2stab及Psstab,注入到各个非线性单元,使得整个变为线性系统,从而保证系统的稳定平衡点为全局稳定平衡点,而不再是小信号稳定平衡点。为了计算得到稳定控制信号P1stab、P2stab及Psstab,对状态变量进行坐标平移,令:

将式(2)改写为以下形式:

由图4可知,当P1、P2及Ps都为零时,系统稳定,则T-1A2必为Lyapunov方程的解,即对于正定对称矩阵Q,必有正定对称矩阵P,使得:

将式(12)代入式(6)可得:
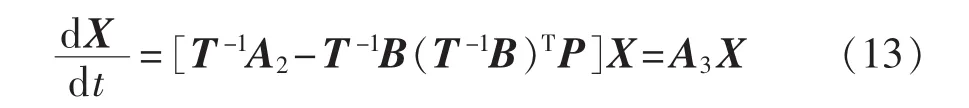
此时整个系统转化为线性系统,并且可以按如下证明系统平衡点为全局稳定平衡点。
由于

其中,“>”表示不等式左边为正定矩阵。
结合式(11)可得:
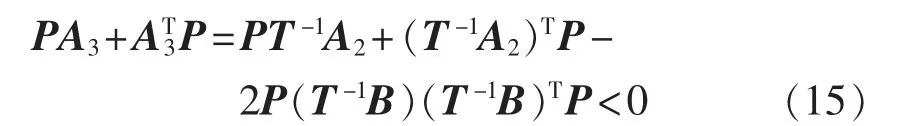
其中,“<”表示不等式左边为负定矩阵。即证明了此时系统全局稳定。
由式(10)整理可得:

4 仿真实验
为了验证前面提出方法的有效性,本文采用MATLAB/Simulink搭建了仿真实验模型,其系统结构如图2所示,系统参数同第2节,变换器的开关频率为10 kHz,Q取10-6I6(I6为6阶单位对角矩阵)。仿真实验结果如图6—9所示。
如图6所示,当系统没有稳定模块,负载P1=3000 W、P2=2500 W时,由式(4)得系统状态矩阵A的特征值为-16.06±j375.25、-1.80±j124.87、-0.80±j195.91,系统处于稳定区域,系统稳定运行。在0.35 s时,负载功率上升至P1=3000 W、P2=4000 W,系统的特征值为-15.63±j375.15、-0.08±j124.47、2.07±j195.76,系统运行于不稳定区域,电压u1、u2发散,并逐渐扩散到直流母线电压un。

图6 负载从P1=3000 W、P2=2500 W跃升至P1=3000 W、P2=4000 W时的系统响应(无稳定模块)Fig.6 System response to load step change from P1=3000 W,P2=2500 W to P1=3000 W,P2=4000 W(without stabilization module)
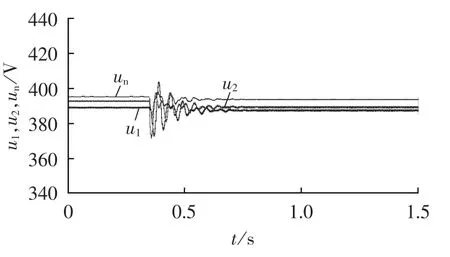
图7 负载从P1=3000 W、P2=2500 W跃升至P1=3000 W、P2=4000 W时的系统响应(有稳定模块)Fig.7 System response to load step change from P1=3000 W,P2=2500 W to P1=3000 W,P2=4000 W(with stabilization module)

图8 负载从P1=3000 W、P2=2500 W跃升至P1=3000 W、P2=4000 W时的稳定功率P1stab(有稳定模块)Fig.8 Waveform of P1stabwhen load changes abruptly from P1=3000 W,P2=2500 W to P1=3000 W,P2=4000 W(with stabilization module)

图9 负载从P1=3000 W、P2=2500 W跃升至P1=3000 W、P2=4000 W时的稳定功率P2stab(有稳定模块)Fig.9 Waveform of P2stabwhen load changes abruptly from P1=3000 W,P2=2500 W to P1=3000 W,P2=4000 W(with stabilization module)
当系统有稳定模块时,在0.35 s时,负载功率上升至P1=3000 W、P2=4000 W,虽然进入了小信号分析的不稳定区域,但系统在反馈控制作用下,由式(13)可得系统的特征值为-11.49±j375.29、-11.05±j125.81、-10.40±j196.79,系统稳定,负载电压 u1、u2及直流母线电压un仍能维持稳定。
负载功率突变前后,稳定功率P1stab、P2stab分别如图8和图9所示。稳定运行时P1stab和P2stab的数值都非常小,并不改变系统的稳态平衡点。即使在暂态过程中,稳定功率P1stab、P2stab的最大值相对于负载消耗功率P1=3000 W、P2=4000 W也是很小的。因此,本文所提出的方法仅需要小的稳定功率就可以确保整个系统的稳定,这是因为稳定模块的输入包含系统的所有状态变量,可以从系统全局的角度产生适当的稳定功率。
5 结论
本文建立了直流微电网的简化数学模型,其小信号稳定性分析强调,负载功率不能过大从而进入不稳定区域,否则将导致系统故障和损坏。为了在不改变系统参数的同时扩大系统的稳定区域,本文提出了一种基于反馈线性化的稳定方法。该方法基于Lyapunov稳定性理论,通过测量系统的状态变量,计算出稳定功率信号,并注入到每个负载的参考功率上,通过反馈控制,使得整个系统线性化,确保了整个系统的全局稳定。该方法不依赖负载的类型,稳定控制器仅依赖系统的网络结构和参数,且可以扩展应用于多电源多负载的系统。仿真实验结果验证了该方法的有效性。

