计及蓄电池使用寿命的微电网经济调度模型

刘春阳 ，王秀丽 ，刘世民 ，祝振鹏 ，吴 雄 ，段 杰 ，侯 菲 ，谢林红

（1.西安交通大学 电气工程学院，陕西 西安 710049；2.北京北变微电网技术有限公司，北京 100093）

0 引言

微电网是一个由多种分布式电源、储能系统和可控负荷组成的相对独立的低压电网，包含并网运行方式和孤岛运行方式［1］。随着能源危机加剧和环境污染日益严重，微电网作为一种新型能源网络化供应和管理技术，受到越来越多的关注。微电网中的储能装置在平衡新能源出力波动、保证电网安全运行、提高供电质量和提高微电网经济性等方面发挥了重要作用。包含储能装置的微电网经济性问题成为近年国内外学者研究的热点。

文献［2-3］涉及考虑蓄电池的微电网经济调度，但没有考虑蓄电池的使用寿命。另外一些文献考虑蓄电池寿命的微电网经济调度，但为简化计算，很多是限定调度周期内蓄电池的循环次数［4-6］，将剩余容量限定在一定范围内［7-8］，或规定寿命为一固定的年数［9］，这仅是对蓄电池寿命的定性认识。国际上在预测蓄电池寿命时，应用较多的是雨流计法计算循环次数［10-13］，但是目前没有任何实验表明雨流计法的正确性［14］，而且雨流计法相对比较复杂，常应用于储能装置的定容和已知运行数据的寿命统计［15］，文献［16］也将雨流计法应用到储能装置定容当中。文献［17］应用帕克特寿命内总吞吐量模型来模拟蓄电池使用寿命，并以此为基础寻找延长电池使用寿命的方法，但是文献中为了去掉寿命累计的后效性，做了一定简化，导致存在一定的方法误差。吞吐量法［18］是对蓄电池实验的总结，吞吐量法认为蓄电池在不同放电深度下，其在寿命内充放电的总电量变化不大，将寿命内总吞吐量看作一个定值，即不同放电深度下的吞吐量的均值。吞吐量法简单易行，满足很多计算的要求，又有实验依据，对于只需要粗略计算的模型是很好的方法。但是实际运行中会有很多因素影响蓄电池的寿命，将影响蓄电池寿命的因素以加权的方式考虑进来，得到改进后的加权吞吐量法，这样在保持吞吐量法简单易行的基础上，使得模型更加准确。

本文以风机、光伏、蓄电池、微型燃气轮机、柴油发电机和燃料电池组成的微电网为研究对象，建立并网运行方式下的微电网经济调度模型。模型中应用加权吞吐量法预测蓄电池的寿命，将蓄电池的寿命因素考虑到微电网的经济调度中。模型以运行成本最小为目标函数，同时考虑功率平衡、备用及不同元件的约束条件，应用混合整数规划算法对模型进行求解。通过算例结果，证明了本文的方法使微电网经济调度更加精确，提高了微电网的经济性。

1 微源出力模型

本节介绍微电网中常用的几种电源出力模型。

1.1 风机模型

风机的出力与风速的关系［19］可以由式（1）近似表示：

其中，vci、vco、vr分别为切入风速、切出风速和额定风速；Prated_WT为风机额定功率。

1.2 光伏模型

在标准测试条件下，光伏发电的出力可以由式（2）表示：

其中，GSTC、TSTC分别为标准测试条件中的太阳辐射照度和电池温度；Gc为工作点的太阳辐射照度；Tc为工作点的电池温度；PSTC为标准测试条件下的光伏额定发电功率；k为功率温度系数。

1.3 微型燃气轮机模型

微型燃气轮机的燃料成本函数如下：

其中，Cnl为天然气价格；L为天然气的热值；PMT（t）为t时刻微型燃气轮机的输出功率；ηMT（t）为t时刻的微型燃气轮机的发电效率；Δt为每个时段的时长。

1.4 燃料电池模型

燃料电池发电的燃料成本函数与微型燃气轮机的相似，成本函数如下：

其中，PFC（t）为 t时刻燃料电池的输出功率；ηFC（t）为 t时刻的燃料电池发电效率。

1.5 柴油发电机模型

柴油发电机的燃料成本与传统火力发电类似，可以表示为柴油发电机的输出功率的二次多项式，其燃料成本可以用下式表示：

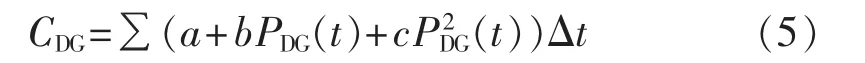
其中，a、b、c为费用函数的系数，可以由厂家提供或者拟合得到；PDG（t）为柴油发电机的输出功率。

1.6 蓄电池出力模型

蓄电池在t时刻的剩余能量跟其前一时刻t-Δt的剩余能量以及其从t-Δt到t时刻的充放电量有关，在充放电的过程中，蓄电池的剩余能量计算公式为：

其中，E（t）、E（t－1）分别为 t、t-1 时刻的蓄电池剩余能量（kW·h）；Pch、Pdh分别为蓄电池的充电功率和放电功率；ηch、ηdh分别为蓄电池的充电效率和放电效率；σ为蓄电池的自放电率。

2 蓄电池的寿命模型

蓄电池的寿命一般是由厂家给出的不同放电深度下的循环次数来表示，蓄电池总的循环次数函数如下：

其中，hDOD为蓄电池的放电深度；a1—a5为由生产厂家提供的参数。

但蓄电池通常会频繁地充放电，不能保证每次的放电深度都是一样的，给计算循环次数带来困难。

吞吐量法是针对蓄电池运行中循环次数难以统计而提出的简单易行的寿命预测方法，其寿命的计算公式如下：

其中，Ethroughput为蓄电池寿命内总的能量吞吐量；Erated为蓄电池的额定容量；ntest为对蓄电池的不同放电深度测试的个数；hDODi为蓄电池第i次测试的放电深度；Ni为蓄电池第i次测试总的循环次数。

其中，不同放电深度的循环次数和对应的总能量吞吐量由厂家给出［20］。

假设蓄电池总的能量吞吐量为一定值，则寿命损耗系数公式如下：

其中，Eloss为计算周期内蓄电池的能量吞吐量，如式（10）所示。

其中，T为计算的时间周期；P（t）为蓄电池在t时刻的充放电功率。

简单的吞吐量法可以粗略地计算出蓄电池的使用寿命，但是实际蓄电池的使用寿命会受到一些因素的影响，经济调度中最主要的影响因素就是蓄电池的荷电状态（SOC）值［21］。蓄电池充或放出相同能量，在荷电状态较低的情况下对蓄电池寿命的损耗较大，在荷电状态较高的情况下对寿命的损耗较小。蓄电池的寿命损耗权重与荷电状态的关系如图1所示［22］。

图1 蓄电池SOC因素的寿命损耗权重Fig.1 Curve of lifetime loss weight vs.battery SOC

从图1可以看出，在荷电状态小于0.5左右时，蓄电池每充或放1 kW·h电能，实际上对电池寿命的损耗要大于1 kW·h；而荷电状态接近1时，其他条件相同情况下，蓄电池每充或放1 kW·h电能，对寿命的损耗在0.5 kW·h左右。2种情况下的寿命损耗权重差距较大。

考虑蓄电池寿命损耗权重之后的蓄电池等效能量吞吐量，如式（11）所示。

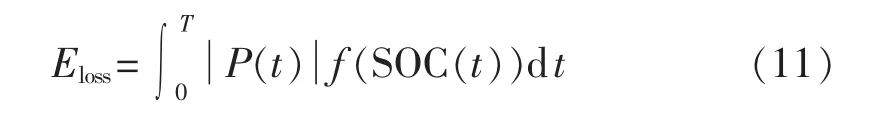
其中，f（SOC（t））为与荷电状态相关的蓄电池寿命损耗权重。

将式（11）代入式（9），即可得到考虑蓄电池荷电状因素的寿命损耗系数公式。

改进后的吞吐量法，在保持原有简单易行的特点外，考虑了影响蓄电池寿命的荷电状态因素，使得模型更加精确，为微电网的经济调度优化提供依据。

3 微电网经济调度模型

本节以费用最少为目标，综合考虑系统和各微源的约束条件，建立了在并网条件下的微电网经济调度模型。

3.1 目标函数

并网条件下微电网模型的目标函数是运行周期内的费用最少，如式（12）所示。

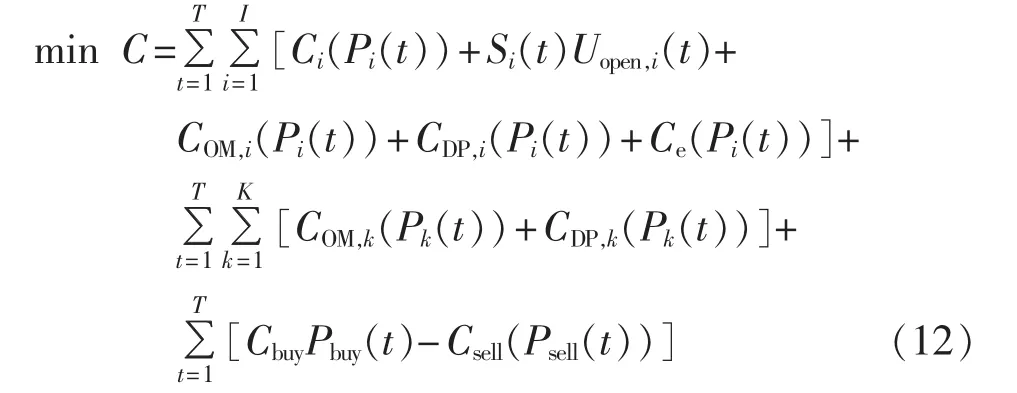
其中，T为调度时间周期；I为可控电源总数；K为储能装置总数；Pi（t）为可控电源出力，Pk（t）为储能装置出力；Ci（Pi（t））为可控电源燃料成本函数，包括微型燃气轮机、柴油发电机和燃料电池；Ui（t）为t时刻可控电源运行的0-1决策变量，0表示不运行，1表示运行；Si（t）为可控电源启动成本；Uopen，i（t）为 t时刻可控电源启动的 0-1 决策变量，1 表示启动；COM，i（Pi（t））、CDP，i（Pi（t））、Ce（Pi（t））分别为可控机组的维护费用、折旧成本和环境成本；COM，k（Pk（t））、CDP，k（Pk（t））分别为储能装置的维护费用、折旧成本；Cbuy、Csell分别为微电网从外部购电和售电的电价；Pbuy（t）、Psell（t）分别为微电网从外部购电和售电的功率。

式中的可控机组维护费用、折旧成本和环境成本的函数见式（13）—（15）。

其中，Caz，i为第i个可控电源的单位容量安装成本的现值（本文所有费用都折算到现值）；ki为第i个微源的容量因数；ni为第 i个微源的使用年限；KOM，i为第i个微源的单位电量运行维护成本系数；Vj为第j项污染物的单位排放费用；Qij为第i个微源单位电量的第j项污染物排放量；m为污染物的种类。

式中的储能装置的维护费用、折旧成本函数见式（16）、（17）。

其中，KOM，k为第k个蓄电池组的单位电量运行维护成本系数；Erated，k、Prated，k分别为第 k 个蓄电池组的额定容量和额定功率；CE，k、CP，k分别为第 k 个蓄电池组的单位容量和单位功率安装成本的现值；Lloss，k为第k个蓄电池组的寿命损耗系数。

3.2 约束条件

3.2.1 功率平衡和备用约束

a.功率平衡约束：

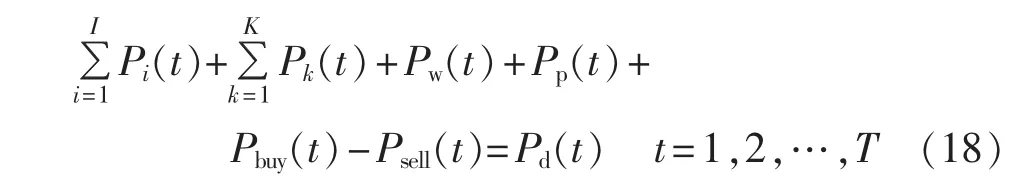
b.备用约束：

其中，Pi（t）、Pk（t）、Pw（t）、Pp（t）、Pbuy（t）、Psell（t）分别为可控机组出力、蓄电池组出力、风电出力、太阳能发电出力和对大电网的购电和售电；Pd（t）为微电网的负荷需求；Rs（t）为微电网的旋转备用需求分别为可控机组出力上限、剩余容量上限、蓄电池最大放电功率、微电网向大电网购电的最大值；Δup，i为可控机组 i的最大向上爬坡率；ηdh，k为第k个蓄电池组的放电效率。

3.2.2 与大电网相关的约束

a.微电网与主网间功率最大容量约束：

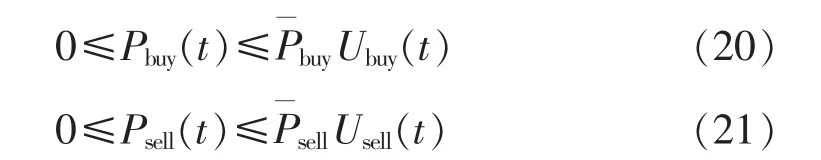
b.购电与售电互斥约束：

3.2.3 与可控机组相关的约束

a.可控电源的输出功率约束：

b.最小停运时间、运行时间约束：

其中，Uopen，i（t）、Uclose，i（t）分别为可控机组 i的开机决策变量和关机决策变量；tMOTi为可控机组i的最小开机时间；tMDTi为可控机组i的最小开机时间；T为调度时间周期。

c.爬坡率约束：

其中，Δdown，i、Δup，i分别为可控机组 i的最大向下和向上爬坡率。

3.2.4 与蓄电池组相关的约束

a.荷电状态约束：

b.满足功率约束：

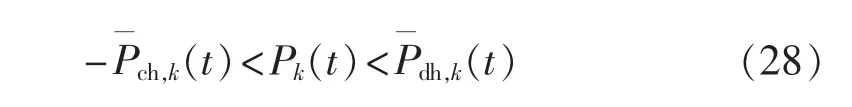
c.周期储能平衡约束：

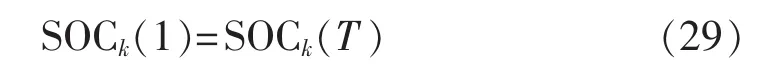
此约束表示，调度周期的始末时刻第k个蓄电池组的荷电状态是相同的。

d.同一蓄电池组的充放电互斥约束：

其中，Udh，k（t）、Uch，k（t）为 0-1 变量，分别表示第 k 个蓄电池组的放电状态和充电状态。

e.不同蓄电池组的充放电互斥约束：

其中，edh，k（t）、ech，k（t）为 0-1 变量；K为蓄电池组的个数。此约束表示当一个蓄电池放电时其他蓄电池组不能充电，反之亦然。

4 模型求解算法

本文应用混合整数线性规划对微电网经济调度进行求解。混合整数线性规划是目前比较成熟的算法，计算时间相对其他算法较少，可以解决相对大型的问题。但是它需要将非线性的问题转化为线性问题来求解，而对非线性约束的处理是混合整数线性规划的难点，本节提出模型中非线性约束的线性化处理方法。

4.1 可控机组出力的处理

可控机组的燃料费用曲线是非线性的，将费用曲线进行分段线性化［23-24］，如图2所示。

图2 费用曲线线性化示意图Fig.2 Schematic diagram of cost curve linearization

如图2所示，可控机组的燃料费用函数C（P）是一个非线性函数，假设将费用曲线分为n段线性的组合，各个分段的分点为P1≤P2≤…≤Pn≤Pn+1，引入一个新的变量zk，将出力P和燃料费用的分段线性函数C′（P）分别表示为式（35）和式（36）。

再次引入一个新的0-1变量yk，其中zk与yk满足下列约束：

4.2 蓄电池寿命损耗处理

为了更准确地计算蓄电池寿命，考虑了蓄电池的荷电状态因素，但是这样就引入了高次变量，见式（11），使得式（17）成为非线性的约束。为了建立混合整数线性规划模型，需要将式（11）进行降次和线性化处理。蓄电池寿命损耗权重示意图如图3所示。

图3 蓄电池寿命损耗权重示意图Fig.3 Schematic diagram of battery lifetime loss weight

从图3中可以看出蓄电池的寿命损耗权重f（SOC（t））是关于蓄电池荷电状态的非线性函数，将之代入式（11）会得到一个至少二次的非线性函数，无法应用到混合整数规划的模型中。为解决该问题，需引入蓄电池寿命损耗权重的累积函数fa（SOC），其公式如下：

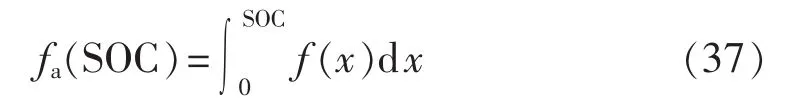
将图3中的蓄电池损耗权重曲线进行累积计算，得到损耗权重曲线的累积曲线，如图4所示。

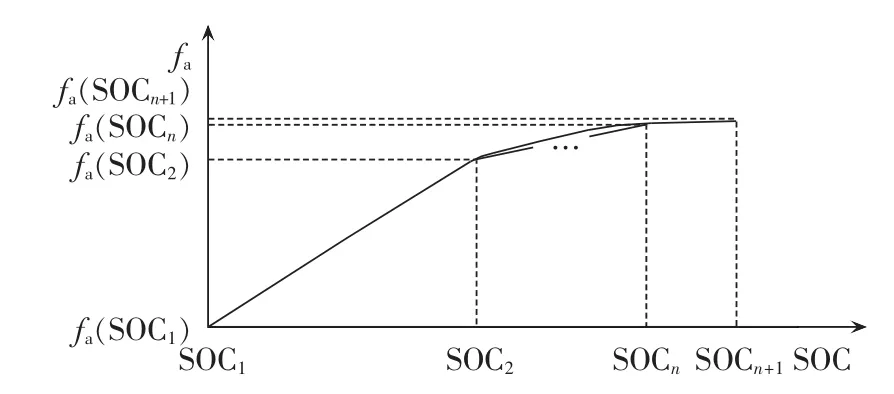
图4 蓄电池寿命损耗权重累积示意图Fig.4 Schematic diagram of cumulative battery lifetime loss weight

应用 4.1节的理论，对图4中的累积曲线进行分段线性化处理，则式（37）的线性逼近函数可以写成：

式（38）、（39）中的参数与式（35）、（36）中的参数处理方式相同。

根据式（38），可以将式（11）写成：

其中，Erated为蓄电池的额定容量；SOC（0）为经济调度之前的蓄电池初始剩余容量。

将式（40）代入式（9）得到的蓄电池寿命损耗函数就是一个一次的分段线性函数，从而将式（17）转化为线性约束。

将微电网经济调度模型中所有的非线性约束进行线性化处理之后，就可以应用混合整数线性规划方法进行求解。目前已有比较成熟的软件（比如LINGO、CPLEX）可以求解混合整数线性问题，本文使用CPLEX对模型进行求解。

5 算例分析

5.1 算例介绍

本文以一个包含风机、光伏发电系统、微型燃气轮机、柴油发电机、燃料电池和蓄电池的微电网为例，进行经济调度计算与分析。

微电网的可控微源基本信息［25-26］如表1所示。可控电源的燃料成本［25-28］曲线如图5所示。微电网中蓄电池的基本参数如表2所示。微电网中的风力发电、光伏发电和负荷预测如图6所示。微电网中采用峰谷平电价，电价如表3所示。假定的污染物排放的征收费用系数［28］如表4所示。

5.2 经济调度结果

在并网运行方式下，得到微电网的经济调度结果如图7所示。

从图7可以看出，风电出力和太阳能发电出力与预测出力曲线一致，说明在已知微电网中风电和太阳能发电日运行成本低，优先发电。微型燃气轮机和燃料电池在谷时段和平时段处于停运状态，在峰时段处于满发状态，说明算例中两者在峰时段的发电成本比大电网低，而在其他时段的发电成本比大电网高。柴油发电机由于发电成本较高，一直处于停运状态，作为微电网的冷备用。蓄电池在谷时段和平时段充电，在峰时段放电，在使成本最优的同时达到削峰填谷的目的。联络线功率是微电网向主网的购售电，由于算例中微电网的负荷比装机容量要大，在一个调度周期内微电网要一直向大电网购电，但是有可控机组和蓄电池的调节，微电网在峰时段的购电减少，微电网整体在大电网中起到削峰填谷的作用。

表1 微电网中的可控微源基本参数Table 1 Basic parameters of controllable microsources in microgrid

图5 可控机组的燃料成本曲线Fig.5 Fuel cost curve of controllable microsources

表2 蓄电池基本参数Table 2 Basic parameters of battery

图6 典型日风力发电、光伏发电和负荷预测Fig.6 Forecasted wind power output，photovoltaic output and load for a typical day

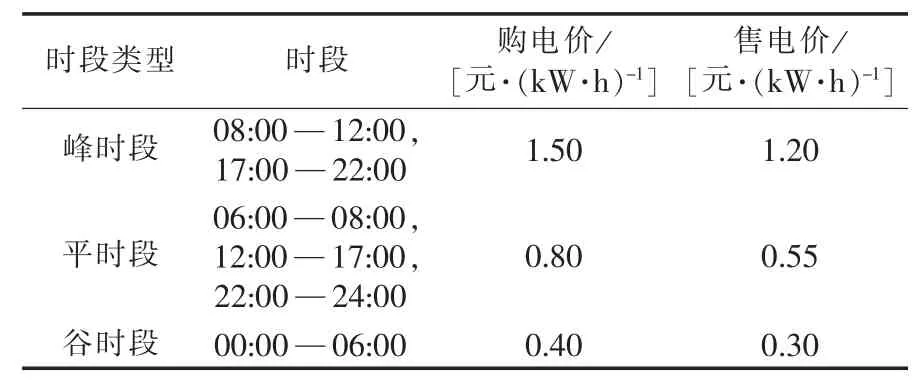
表3 分时段电价Table 3 Tariff of different periods

表4 污染物排放征收费用Table 4 Penalty of different pollutant emissions

图7 微电网并网运行时经济调度结果Fig.7 Results of economic dispatch for grid-connected microgrid

考虑与荷电状态相关的寿命损耗权重之后，得到更加精确的蓄电池模型，对微电网运行提供更准确的依据，最终蓄电池运行的剩余容量变化如图8所示。

图8 考虑和不考虑SOC寿命损耗权重的蓄电池剩余容量对比Fig.8 Comparison of residual battery capacity between with and without consideration of SOC lifetime loss weight

从图8可以看出，考虑与荷电状态相关的寿命损耗权重后，蓄电池的剩余容量整体上比不考虑时要偏高，这是因为在荷电状态较高时，蓄电池的充放电对寿命的损耗相对较小，蓄电池趋向于在高荷电状态状态充放电。

考虑和不考虑荷电状态寿命损耗权重模型的运行成本对比如表5所示，表中不考虑荷电状态寿命损耗权重模型的运行成本实际结果为该模型计算结果考虑蓄电池荷电状态因素后的实际运行成本。

表5 微电网运行费用对比Table 5 Comparison of microgrid operational cost

从表5可以看出，在本文的微电网算例中，考虑荷电状态寿命损耗权重后，微电网各微源的运行费用都有所调整。其中，考虑荷电状态寿命损耗权重模型的蓄电池运行费用比不考虑荷电状态寿命损耗权重模型的计算结果多，结合图8可以得知，蓄电池在高荷电状态时的运行成本较小，按照微电网整体成本最低的原则，在高荷电状态时的充放电会增加，蓄电池的总运行费用会增加。对比不考虑荷电状态寿命损耗权重模型的运行成本计算结果和实际结果可以看出，实际结果中蓄电池的运行费用比计算结果要高，说明不考虑荷电状态寿命损耗权重模型并不精确，由于没有区分蓄电池的荷电状态，蓄电池如果长期在相对低的荷电状态下运行，蓄电池的成本损耗会较高。

考虑荷电状态寿命损耗权重后的模型能更加精确地衡量蓄电池的寿命损耗成本，可以更好地规划蓄电池的运行，使得微电网整体运行费用降低，进一步验证了模型的有效性。

本文算例为一个完整的微电网系统，其中蓄电池的成本为运行成本的一小部分，如果是一个以蓄电池为主体的微电网系统，优化效果会更加明显。

6 结语

本文建立了包含风电、光伏、储能和可控机组的微电网经济调度模型。模型中综合考虑了各单元的燃料成本、启停成本、折旧损耗、维护和环保等因素，将这些因素都折算为成本，这样就可以将一个多目标问题转化为完全以成本最优为目标的单目标问题，模型最终求解得到的是微电网经济调度运行成本的最小值。

微电网模型中考虑了蓄电池的寿命，提出一种加权的吞吐量法来计算寿命损耗，并提出一种可以将之转化为混合整数线性规划问题的方法。文中同时阐述了一种各微源通用的线性化方法。通过这些方法，将微电网模型转化为混合整数规划问题求解。