一种量化评估暂态电压稳定性的指标与方法
侯建兰 ,刘育权 ,谢小荣 ,叶 萌 ,孙英云 ,王 珂 ,张 尧
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.华南理工大学 电力学院,广东 广州 510641;3.广州供电局有限公司,广东 广州 510620;4.清华大学 电机系 电力系统及发电设备控制和仿真国家重点实验室,北京 100084)
0 引言
近年来,国内外发生的电压失稳乃至崩溃事故造成了严重的经济损失和不良的社会影响,对电力系统安全评估提出了新的挑战[1-4]。不少电压崩溃事故源于电力系统在某个运行状态下受到大的干扰后系统电压发生较大偏移,此时由于感应电动机、高压直流(HVDC)装置等具有快速动态响应特性设备的影响导致系统失去稳定[5],属于暂态电压失稳。
目前,国内外学者对电力系统暂态电压稳定性的研究方法主要有扩展等面积法、暂态函数能量法、时域仿真法以及基于风险的评估方法等[6-13]。文献[6]结合时域仿真提出了单机加速面积与减速面积计算方法,并根据临界机组群中单机加速面积与减速面积给出了多机系统等面积稳定判别准则。文献[7]根据带约束动力系统稳定域理论,其受限稳定边界由边界上不稳定平衡点、周期轨和半鞍点的稳定流形以及部分可行域边界构成。根据电力系统结构保持模型,寻找到和故障相关的一个半鞍点,然后以该点能量作临界能量,保证故障后系统满足暂态电压跌落约束。该方法的不足之处在于半鞍点的选取不合适或者所选取能量函数本身的局限性,可能导致分析产生较大误差。文献[8-10]考虑客观运行条件和故障等多种不确定因素的影响,将随机因素与概率分析观点引入暂态分析,提出了基于风险的暂态电压稳定性评估方法,将防止系统暂态电压崩溃而采取的控制措施所造成的控制成本作为系统失去暂态稳定性的严重度。然而该方法包含两方面困难:一方面是预估某特定发电机或负荷停电对应的损失;另一方面在于如何识别预想故障下哪些发电机或负荷会停电以及停电的持续时间。
评估系统暂态电压稳定性的关键在于找出一种合理、实用的评价指标,文献[14]以容易引起暂态电压失稳的电动机电磁转矩-滑差曲线为基础,将故障后的极限切除时间作为系统暂态电压稳定性的衡量指标。由于实际系统中难以获取每一台电动机的电磁转矩-滑差曲线,该方法难以应用于评估实际系统的暂态电压稳定性。
本文以暂态电压稳定的实用判据为基础,提出了评估系统暂态电压稳定性的电压暂降指标,包括单一故障下节点电压暂降指标、多故障集下节点电压暂降指标以及系统电压暂降指标,并给出了将指标应用于实际系统的暂态电压稳定性分析方法。指标的计算可直接利用实际系统运行过程中进行的故障时域仿真结果数据,无需额外的仿真分析。广州电网的算例分析结果体现了不同故障类型、不同负荷模型对系统暂态电压稳定性的影响差异,表明了所提指标应用于评估实际系统暂态电压稳定性的有效性与实用性。
1 电压暂降指标
根据2013年发布,并于同年8月实施的电力系统安全稳定计算技术规范[15]的相关描述,电力系统暂态电压稳定性判据为:在电力系统受到扰动后的暂态过程中,负荷母线电压能在10 s内恢复到0.8 p.u.以上。此外,技术规范建议在实际应用该判据时,可将电压检测点选择在负荷母线处。本文旨在研究电力系统暂态电压稳定性,因此所提量化评估指标不考虑中长期电压稳定。
实用判据包含了故障切除后负荷电压跌落的可接受程度,即低于0.8 p.u.的持续时间不超过10 s。以此判据为基础,提出能够反映电压暂降严重性程度的指标,包括电压暂降严重性指标和电压合格性指标两部分。
1.1 单个故障的节点电压暂降指标
在大扰动故障发生后,系统各母线电压发生偏移,故障切除后母线电压低于限定值的持续时间是衡量故障严重性和系统暂态稳定性的关键所在。设当发生故障 i时节点 j的动态电压为 Ui,j(t),则电压暂降严重性指标 Sei,j、电压合格性指标 Fpi,j分别定义为式(1)和(2):

其中,电压暂降严重性指标Sei,j包含惩罚函数和积分两部分,Di,j为罚函数,对不满足电压稳定判据的惩罚值为p(p>0),其具体取值可根据不同的系统以及时域仿真情况进行调整,取值原则为保证罚函数取值远大于积分项的数值,以明显区分满足与不满足暂态电压稳定判据的节点电压暂降严重性程度,积分项表示低于0.95 p.u.的面积,0.95 p.u.为考虑用电设备允许电压偏移量±5%而设定的负荷侧最低需求电压;t0为故障开始的时间;Δt1、Δt2分别为故障 i时节点 j电压低于 0.95 p.u.、0.8 p.u.的持续时间;电压合格性指标Fpi,j根据暂态电压稳定判据来判断故障条件下节点电压是否合格,若电压合格则取值为1,电压不合格则取值为0。
罚函数的目的是惩罚不满足暂态电压稳定判据的节点,分为合格和不合格2档:若节点j不满足暂态电压稳定判据,即扰动后的暂态过程中负荷母线电压下降持续低于0.8 p.u.的时间超过10 s,惩罚为p;根据暂态电压稳定判据其他情况视为电压稳定,罚函数取值为0。
式(1)表明那些具有长的暂降持续时间和小的暂降幅值的故障具有较高的暂降严重性指标,因而严重性指标能够表征故障的实际影响程度。
定义式(1)和(2)中的节点电压动态 Ui,j(t)可通过时域仿真得到。因此,上述Sei,j的具体实现采用时域仿真得到的数据,其中积分计算也可改为求和公式,即式(1)可等效为式(3):

其中,ΔT为时域仿真计算步长;ki,j(t)=0 表示故障 i条件下节点 j在 t时刻的电压大于 0.95 p.u.,ki,j(t)=1表示电压小于等于0.95 p.u.。
1.2 多个故障集下的节点电压暂降指标
对于系统中的一个节点,不能简单地从一次故障后节点电压恢复情况判断其暂态电压稳定性,需要综合考虑多个典型故障后节点电压恢复情况。因此,需设定一个典型故障集,该故障集包含多个故障,在考虑M个典型故障下,任一节点j的电压暂降严重性指标 Se∑,j和电压合格性指标 Fp∑,j如式(4)所示:

其中,考虑M个典型故障的节点电压合格性指标Fp∑,j是所有故障形势下节点j电压合格性指标Fpi,j的连乘运算,其含义为当且仅当节点j在所有典型故障下暂态电压均合格时满足Fp∑,j=1,只要在某故障下节点暂态电压不合格,则认为该节点暂态电压不合格,此时 Fp∑,j=0;wi为故障 i的权重值,满足式(5)。

故障集中的故障可根据发生概率和严重性,采用不同的权重。例如,若将所给典型故障分为N-1故障和N-2故障,考虑到N-1故障发生的概率比N-2故障大,假设在进行计算时N-1故障的权重设为N-2故障的α倍,前k个为N-1故障,后M-k个为N-2故障,设N-2故障的权重为w2,结合式(5)求解出,则式(4)变形为式(6):

评估系统中各节点的电压暂降严重性程度,可将各节点的电压暂降严重性指标进行排序,Se∑,j越大,说明该母线故障情况下电压暂降越严重,暂态电压稳定性越差。根据Fp∑,j取值评估节点暂态电压是否稳定,取值为1表明该节点暂态电压稳定,反之则不稳定。
1.3 系统电压暂降指标
系统电压暂降指标需要综合考虑系统中需要重点关注的所有负荷节点。因此故障i时系统的电压暂降严重性指标 Sei,∑与电压合格性指标 Fpi,∑以及系统电压合格率 Pri,∑定义为式(7):

其中,电压合格性指标Fpi,∑表示在系统所关注的N个节点中电压合格的总节点数;电压合格率Pri,∑表示电压合格的节点占所关注节点总数的百分比;φj为节点j的权重值,考虑到10.5 kV负荷母线的重要性基本一致,其值取为1/N。
综合所有故障后系统的电压暂降严重性指标Se与电压合格性指标Fp以及电压合格率Pr如式(8)所示:

根据系统的电压暂降指标公式推导可知,电压暂降严重性指标的数值可反映暂态电压稳定性,数值越大,稳定性越差。电压合格性指标能够表示系统暂态电压是否完全稳定,若数值为N,即所有被关注节点暂态电压均合格,则暂态电压稳定,反之则暂态电压失稳。电压合格率表示系统中暂态电压合格的百分数。
与现有的指标[16]相比,本文所提出的指标具有以下优势:
a.可对节点和系统进行电压暂降严重性评估;
b.暂态电压严重性可全面分析综合考虑各种典型故障;
c.通过电压合格性指标明确给出节点和系统暂态稳定与失稳的界限;
d.在同一故障下,可横向比较系统中各节点在该故障下的电压暂降严重性程度;
e.通过比较同一节点在不同故障下的严重性指标,可判断该节点与故障发生点的联系紧密程度,严重性指标数值越大,越容易失稳,表明此故障对所研究节点影响越大;
f.通过比较不同故障形式下的系统电压暂降严重性指标,可评估各类故障对系统的影响程度,系统电压暂降严重性指标越大,说明该故障越容易引起暂态电压失稳或者引起电压失稳的范围越大。
2 暂态电压稳定性评估方法
暂态电压稳定性评估方法包括前期的数据设定、时域仿真分析、电压暂降严重性指标与电压合格性指标计算以及暂态电压稳定性判断。
将电压暂降指标应用于实际电网进行暂态电压稳定性评估的流程如图1所示,具体实施步骤如下。
步骤1:收集电网运行数据,包含系统元件参数、网络拓扑结构信息、负荷情况等。
步骤2:根据实际需要,对所研究电网分析设定运行方式集Os、典型故障集Fs以及节点集Ns。
步骤3:采用PSD-BPA时域仿真分析软件分别对特定运行方式下各故障进行时域仿真分析,记录所研究节点在故障发生后的电压情况。
步骤4:根据故障后节点电压的时域仿真结果,采用MATLAB进行电压暂降严重性指标和电压合格性指标计算。
步骤5:根据电压合格性指标计算结果,判断节点和系统的暂态电压稳定性。

图1 暂态电压稳定性评估流程图Fig.1 Flowchart of transient voltage stability assessment
3 算例分析
3.1 算例简介
为了验证本文所提指标用于评价实际电网暂态电压稳定性的量化性与有效性,算例采用广州电网2016年规划数据。2016年广州电网以北郊、木棉、花都、增城、狮洋和广南6个500 kV变电站作为主要支撑。本文重点研究不同故障类型、不同电动机负荷比例对暂态电压稳定性的影响。
以500 kV线路N-1故障和500 kV线路N-2故障为典型故障进行电网暂态电压稳定性分析。具体为:故障1,北郊—花都线路花都侧发生三相短路,0.1 s后跳单回线路;故障2,花都—从西换流站线路从西侧发生三相短路,0.1 s后断开双回线路。
算例综合负荷模型是感应电动机负荷+恒阻抗负荷,根据构成比例不同分以下几种模型进行仿真分析以及电压暂降指标计算,如表1所示。

表1 不同的综合负荷模型Table 1 Different integrated load models
具体感应电动机负荷参数如下:转子电阻RR=0.02 p.u.,定子电抗 XS=0.18 p.u.,转子电抗 XR=0.12 p.u.,惯性时间常数 TJ=2 s,初始滑差 S0=0.0116 p.u.。
3.2 广州电网暂态电压稳定性分析
3.2.1 时域仿真分析
以广州林和变电站10.5 kV负荷母线为例,采用相同的综合负荷模型,在发生故障1、故障2时其母线电压(标幺值,后同)如图2所示。从图中可知,故障2对林和暂态电压的影响大于故障1,尤其在负荷模型采用55%电动机+45%恒阻抗的综合模型2时差异明显,故障1切除后母线电压最终能恢复到稳态水平,而故障2切除后母线电压一直保持在0.4 p.u.左右,发生暂态电压失稳。

图2 相同负荷模型条件下不同故障时母线暂态电压对比Fig.2 Comparison of transient bus voltage between different faults in same load model condition

图3 相同故障条件下不同负荷模型时域仿真对比Fig.3 Comparison of time domain simulation among different load models in same fault condition
故障1、故障2在表1所述的各种综合负荷模型下的仿真结果图3所示。 其中,图3(a)、(c)分别为故障1、故障2时林和站10.5 kV母线电压,图3(b)、(d)分别为故障 1、故障 2时林和站负荷无功的变化情况。
从图3可看出电动机负荷比例越大,故障后暂态电压降落越严重,由图3(c)可简单判断出在故障2条件下开始引起林和母线暂态电压失稳的综合负荷模型为:55%电动机+45%恒阻抗。
3.2.2 电压暂降指标计算与暂态电压稳定性分析
作为一个大型电网,通过观察每条母线的电压来判断系统暂态电压稳定性不具备可实现性。采用本文提出的单一故障节点电压暂降指标计算方法,以林和10.5 kV母线为例,计算出故障1、故障2时在各种负荷模型下的电压暂降严重性指标,根据经验,在电压暂降指标计算中罚函数取值p=10;采用多故障集下节点电压暂降指标计算方法,计算出综合考虑故障1、故障2时林和10.5 kV母线的节点总指标,且故障1的权重取为故障2的2倍,即式(6)中α=2(下同)。林和10.5 kV母线的电压暂降指标计算结果如表2所示。

表2 林和10.5 kV母线的电压暂降严重性指标Table 2 Voltage sag severity index of Linhe 10.5 kV bus
由于电压暂降严重性指标超过惩罚函数值10的属于暂态电压失稳,因此从表中数据可知,在电动机负荷比例达到55%及以上时,林和10.5 kV母线发生失稳。
按照系统电压暂降指标计算方法算出故障1、故障2在不同电动机比例负荷模型时的系统电压暂降严重性指标、系统电压合格率分别如表3、表4所示。
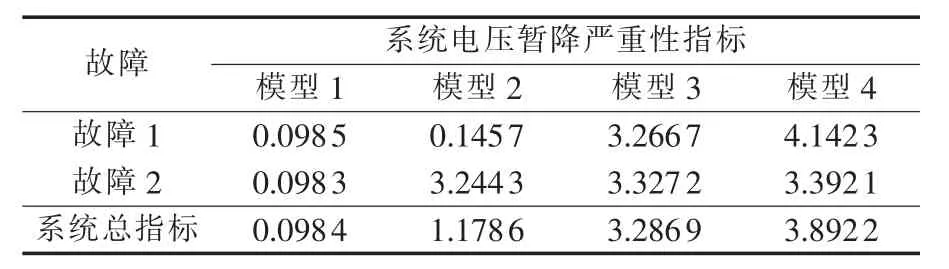
表3 系统电压暂降严重性指标Table 3 System voltage sag severity index

表4 系统电压合格率Table 4 System voltage qualification rate
从表3中数据可知,随着电动机负荷比例的增加系统总电压暂降严重性指标数值增大,表明电动机比例越大越易引起系统暂态电压失稳。由表4可知,系统电压合格率也随电动机比例增加而下降,由此从另一侧面证明了感应电动机负荷对系统暂态电压稳定性的重要影响。
4 结语
为定量评估实际大规模电网暂态电压稳定性,本文提出了基于电压暂降指标的量化评估方法。根据电力行业大扰动下暂态电压稳定判据提出了电压暂降指标,包括电压暂降严重性指标和电压合格性指标,主要用于评价节点或系统在各种故障形式下的暂态电压稳定性,并且可用于研究不同电动机负荷比例对系统暂态稳定性的影响。广州电网综合负荷模型中电动机负荷比例达到55%及以上时,故障切除后系统发生暂态电压失稳。
通过广州电网2016年规划数据的仿真分析与计算,详细说明了本文所提方法具有简洁、定量、准确等优点,适用于工程上快速对电网暂态电压稳定性进行量化评估。

