基于纵向阻抗的双端量故障测距新算法

夏经德 ，张向聪 ，黄新波 ，康小宁 ，邵文权 ，刘毅力

（1.西安工程大学 电信学院，陕西 西安 710048；2.西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

输电线路精确的故障定位可以极大地缩短检修人员的巡线时间，对电力系统的安全稳定和经济运行具有十分重要的意义。因此，故障测距算法成为国内外研究的热点。

现有的故障测距算法从原理上可以分为故障分析法、行波法［1-4］和智能测距算法［5-6］，而从所需的信息来源又可分为单端量法［7-9］和双端量法［10-13］。 行波法可靠性高、稳定性好，但是存在很多尚待解决的技术问题，例如：波头的可靠提取；故障点反射波的识别和标定等。智能测距算法创新性强，但是在原理上还不够完善和成熟，尚不能投入实际应用。单端量法由于信息不足，测距精度始终受到对端系统和过渡电阻的影响。双端量法不受上述因素的影响，测距精度高，受到人们的普遍重视。但是，双端量法也面临着一些亟待解决的问题，例如：双端量法大多计算过程复杂，需要多次迭代［10］和伪根识别［11］；测距精度容易受高压输电线路参数变化的影响［13］等。

针对以上双端量法中存在的问题，本文提出了一种双端量故障测距新算法。该算法在三相线路解耦后的双端口装型等值电路中，利用纵向阻抗与故障距离的关系，建立双端量故障测距方程式，并根据方程式中线路两端的电压、电流故障分量，线路参数以及系统阻抗之间的关系实现故障测距计算，同时能够实时计算出系统阻抗。该算法也能够利用故障前线路两端的电压和电流相量计算出线路阻抗。大量的EMTP仿真结果表明，该算法不受线路参数和系统阻抗变化、故障类型、故障电阻和故障距离的影响，测距精度高，具有较好的稳定性。

1 测距的基本原理

图1为双端电源供电系统故障分量网络中三相线路解耦（详细解耦过程参见文献［14］）后，单相接地故障时的等值电路图。为了提高本文算法的测距精度，本文在故障点两侧采用装型等值电路。

图1 解耦后单相接地故障时的等值电路图Fig.1 Decoupled equivalent circuit diagram of system with single-phase grounding fault

图中，z11和y11分别为故障点左侧装型等值电路中线路单位长度的正序阻抗和正序电纳；z12和y12分别为故障点右侧装型电路中线路单位长度的正序阻抗和正序电纳；ΔUMφ∑和 ΔUNφ∑分别为解耦后线路两端的电压故障分量；ΔIMφ和ΔINφ分别为线路两端的电流故障分量；ΔIMφC和 ΔINφC分别为线路两端流经对地电容支路的电流分别为解耦后线路两侧的正序系统阻抗；-UF和IF分别为故障点等效工频电势和故障电流；U′F为故障点线路上实际工频电压值；RF为故障电阻；D为线路的地理长度；d为故障距离。

图1中，三相线路解耦后两端的电压ΔUMφ∑、ΔUNφ∑分别为：

其中，UM0和UN0分别为故障后线路两端的零序电压；zm和z0分别为线路单位长度的互阻抗和零序阻抗。 式（1）的推导过程见文献［14］。

线路两端流经对地电容支路的电流分别为：

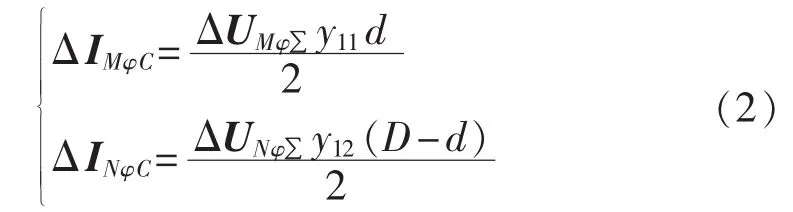
将图1中的并联支路作简化处理：M侧系统阻抗Z′1M和紧邻的并联支路导纳y11d/2并联，并联后的阻抗记为Z″1M；系统阻抗Z′1N和紧邻的并联支路导纳 y12（D－d） /2 并联，并联后的导纳记为 Z″1N；故障点处的3条并联支路组成的含源一端口网络按照戴维南定理等效成电压源和电阻的串联，等效电压源的电压记为-U‴F，故障点处的电压记为U″F，等效电阻记为R′F。简化后得到的等值电路图见图2。

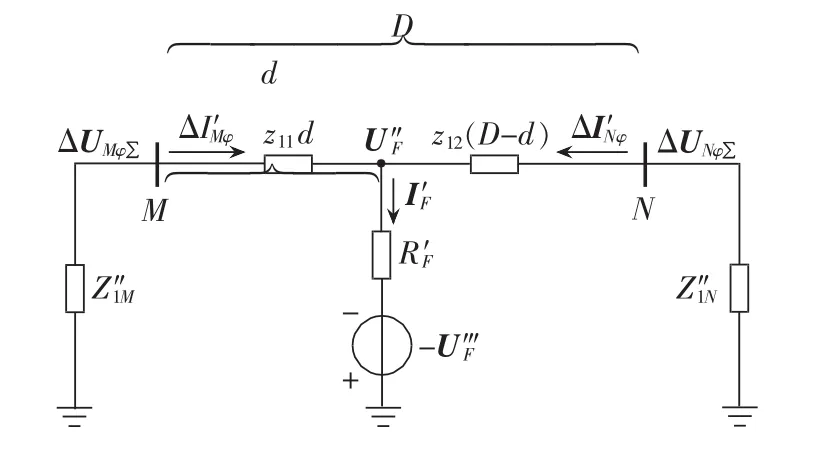
图2 简化后的等值电路图Fig.2 Simplified equivalent circuit diagram

图2中，简化后的等值系统阻抗Z″1M、Z″1N的表达式分别为：

三相线路解耦后线路两端的电压差为：

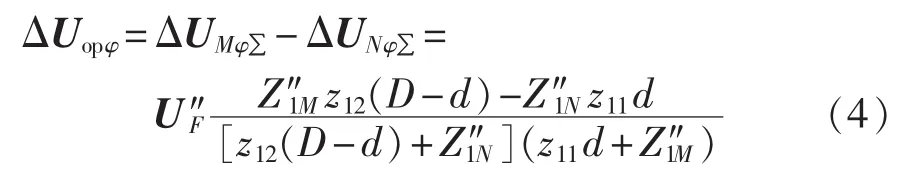
根据基尔霍夫电流定律可知，图2中线路两端的电流分别为：

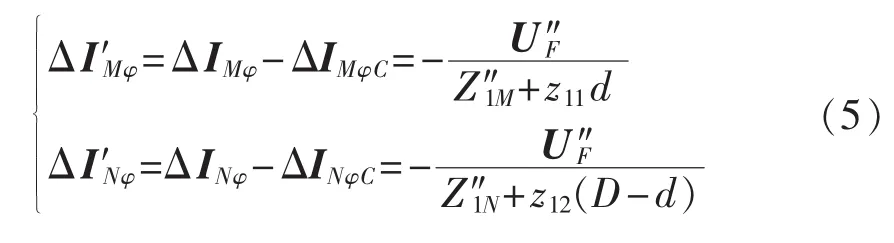
则线路两端的电流和的表达式为：

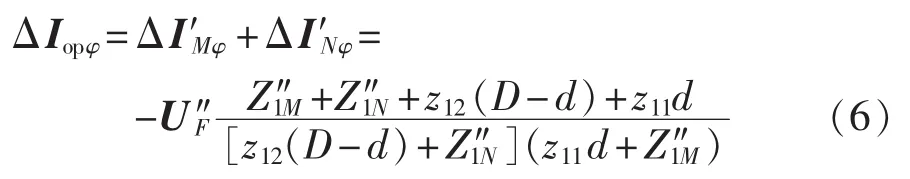
将式（4）和式（6）代入纵向阻抗的表达式，可得双端口Π型等值电路中纵向阻抗的表达式为：

转化式（7）可以求出故障距离的表达式为：

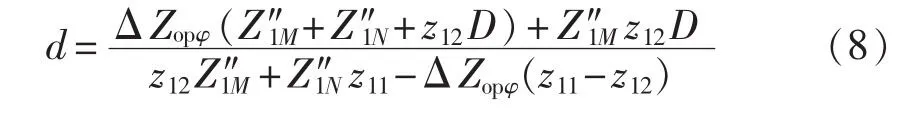
根据式（8）即可以实现故障测距。

2 线路参数计算

由以上测距方程式的推导过程可知，准确的线路参数是实现精确测距的关键。现有的测距算法一般都按照给定的线路参数进行测距计算。而实际上，线路参数不仅会随着环境条件的变化而变化，而且与系统运行情况有关，存在着不确定性，故本节利用故障前的电气数据，通过实时计算的方法获得线路参数。系统故障前的单相线路的等值电路图如图3所示，图中 UM、UN、IM、IN分别为系统正常运行时线路两端的电压和电流；Z为线路阻抗；Y为线路导纳。

图3 单相线路的等值电路图Fig.3 Equivalent circuit diagram of single-phase transmission line

具有分布参数特性的线路两端的电压、电流之间的关系为：

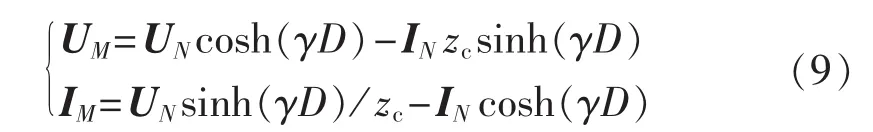
其中，γ为线路的传播系数；zc为线路的波阻抗；D为线路的地理长度。

根据式（9）可得：

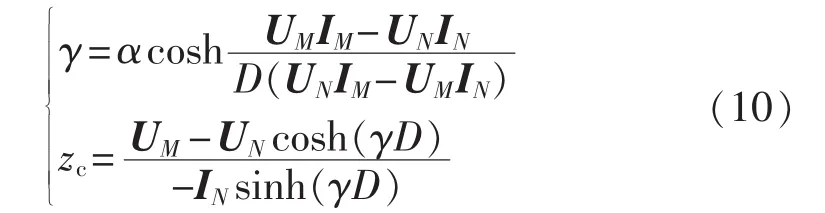
z1、y1分别为分布参数特性下单位长度的线路正序阻抗和正序电纳，则有：

由于本文算法在集中参数线路模型中建立，因此应该利用线路的集中参数进行测距计算，提高测距精度。本节利用修正参数计算方法（公式来源请参阅文献［15］）求得修正后集中参数线路模型中线路单位长度正序阻抗和正序电纳。修正系数如式（12）所示。

其中，r1、x1、b1分别为在线测量的线路单位长度的正序电阻、电感和电纳值；L为要对参数进行集中化处理的线路的地理长度。集中参数线路模型中线路单位长度的正序阻抗和正序电纳为：

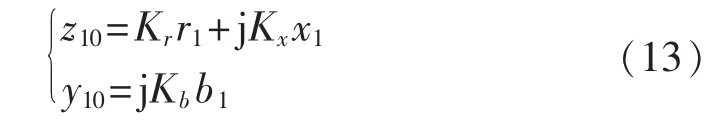
z10、y10即为利用系统正常运行时线路两端的电压、电流相量实时在线测量并对测量结果进行修正的线路参数，它能够反映系统运行方式和运行环境的变化。显然，采用式（12）进行修正后的参数所形成的Π型等值电路，实际上已经考虑了分布电容的影响，使测距结果更加可靠、准确。

3 故障测距算法的实现

根据式（12）和式（13），在已知线路长度 L的条件下，才能求得修正后的线路参数。故只有在某个故障距离d0下，才可以求出图1中双Π型等值电路中的线路参数。本文采用在不考虑线路分布电容的情况下求解d0。

不考虑线路分布电容影响时，纵向阻抗的表达式为：

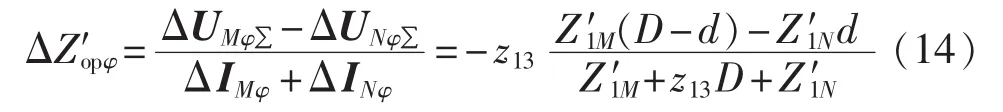
其中，z13为按线路全长修正的线路单位长度的正序阻抗；其他参数参见图1。

根据式（14），不考虑线路分布电容时故障距离d的表达式为：

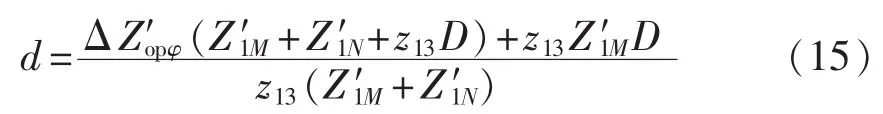
a.利用双端同步相量测量技术，很容易测得线路两端同一时刻的电压和电流，由此可以求得解耦后线路两端测量处电压故障分量 ΔUMφ∑、ΔUNφ∑和电流故障分量ΔIMφ、ΔINφ。然后求得不考虑线路电容时的纵向阻抗的值。

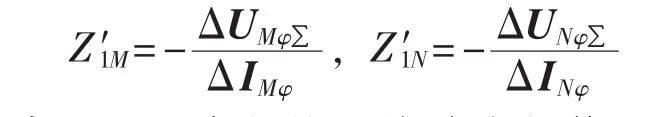
c.令L=D，求得按照线路全长修正的线路单位长度的正序阻抗z13。

d.将求得的单位长度的线路阻抗z13、不考虑线路电容时的纵向阻抗 ΔZ′opφ、系统阻抗 Z′1M和 Z′1N代入式（14），就可以初步求得故障距离d0。

根据初测故障距离d0，修正故障点左侧Π型电路的线路参数，令 L=d0，代入式（12）和式（13）可以求得 z11和 y11；同理，令 L=D-d0，可以求得 z12和 y12。

将 ΔUMφ∑和 ΔUNφ∑的值代入式（2）求得 ΔIMφC、Δ INφC，并代入式（5）求得 ΔI′Mφ、ΔI′Nφ，然后求出考虑线路电容时的纵向阻抗 ΔZopφ。 将 Z ′1M、Z′1N、D 和 d0代入式（3），求得Z″1M和Z″1N的值。将z11、z12、y11、y12、ΔZopφ、Z″1M和Z″1N代入式（8），求出故障距离d。

4 并联电抗器对算法的影响

现代大容量超/特高压电网通常配置一定数量的电抗器以补偿线路电容电流和稳定运行电压。并联电抗器的引入改变了网络结构，会对测距算法产生影响。

图4所示为两端安装并联电抗器的输电线路发生故障时的等值电路图。图中，M侧并联电抗器安装处的电压为ΔUMφ∑，N侧并联电抗器安装处的电压为ΔUNφ∑，则图4可以简化为图5。

图5中，ΔIM″φ和 ΔIN″φ的表达式为：

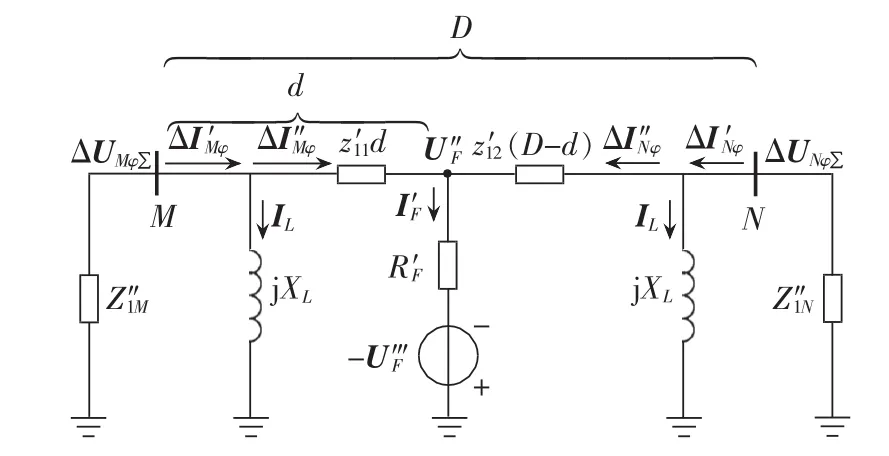
图4 线路两端安装并联电抗器的等值电路图Fig.4 Equivalent circuit diagram of transmission line with shunt reactor at both ends

图5 线路两端安装并联电抗器简化后的等值电路图Fig.5 Simplified equivalent circuit diagram of transmission line with shunt reactor at both ends

显然，并联电抗器的引入对线路参数也产生了影响。输电线路两端安装并联电抗器后，系统正常运行时的等值电路图如图6所示。图中，流入线路中 的电流 I′M和 I′N的表达式为：

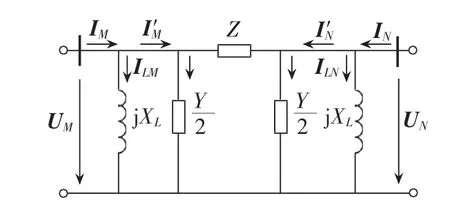
图6 线路两端安装并联电抗器的单相线路的等值电路图Fig.6 Simplified single-phase equivalent circuit diagram of transmission line with shunt reactor at both ends

5 仿真分析

图7为在ATP/EMTP中搭建的线路两端不安装并联电抗器的仿真模型，具体系统参数为：系统电压等级500 kV，输电线路长度l=400 km；M侧系统正序阻抗ZM1=0.1014+j8.0133，零序阻抗ZM0=0.0448+j 2.6878；N侧系统正序阻抗ZN1=1.128+j16.0391，零序阻抗ZN0=0.0896+j5.019；输电线路参数，z1=0.0108+j0.1113，z0=0.07792+j0.2587。 图8为线路两端安装并联电抗器的仿真模型，模型中线路长度和线路参数与图7相同，系统参数变为ZM1=0.1014+j15.9676、ZM0=0.0448+j11.6303、ZN1=1.128+j16.0391、ZN0=0.0896+j13.7118。电抗器的参数为XL=268.89，XN=69.44。以上参数均为标幺值。

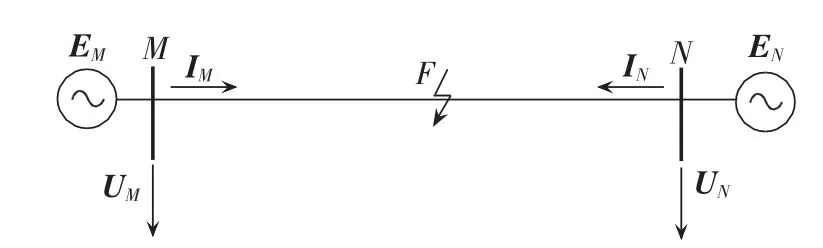
图7 仿真模型图Fig.7 Simulation model

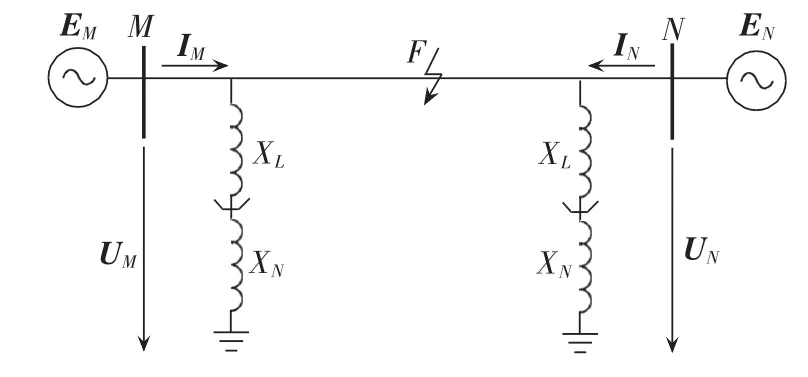
图8 线路两端安装并联电抗器的仿真模型图Fig.8 Simulation model of transmission line with shunt reactor at both ends

采用EMTP进行仿真，数据处理软件为MATLAB。为了验证本文算法的有效性和优越性，本节大部分的仿真结果都以与文献［12］算法对比的形式给出。文献［12］给出的仿真结果都是在Π型电路下仿真得到的，本文的仿真结果在分布参数模型下仿真得到。

为了体现本文测距算法的正确性，图9给出了本文算法在A相单相接地故障、故障距离为350 km时故障距离的计算值变化结果，其横坐标为采样点数，每个采样点计算一个测距结果；纵坐标为故障距离计算值。

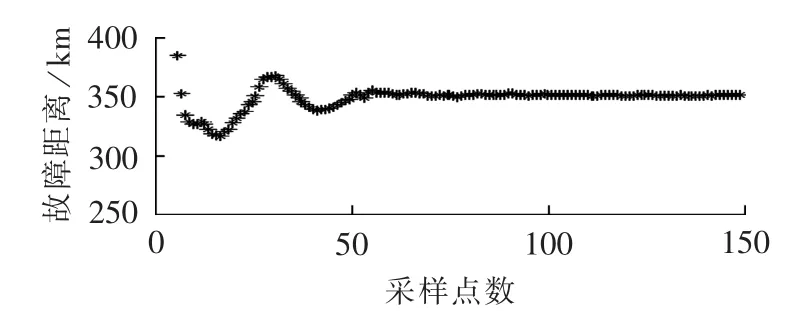
图9 单相接地故障时的故障距离计算值Fig.9 Calculated fault distance for single-phase grounding fault

根据图9，本文算法可以在系统故障后的3个周期以内准确地计算出故障距离，体现了该算法的正确性。

针对本文算法受故障距离、故障类型和故障电阻等参数影响的性能，本文进行了大量的仿真验证，限于篇幅，本节仅列出表1—3的仿真结果。表中，RF为故障电阻，并定义测距的相对误差为：

其中，d为实际的故障距离；d′为仿真故障距离；D为线路地理长度。

表1为文献［12］算法与本文算法在A相单相接地故障时不同故障距离的测距结果和测距误差对比。

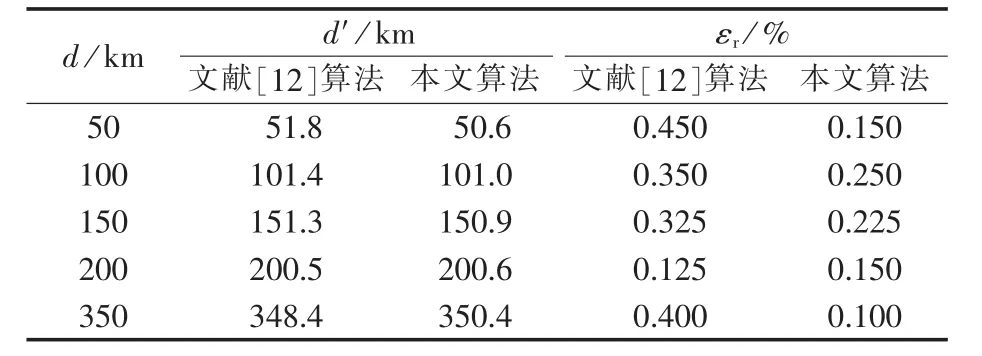
表1 不同故障距离下，2种算法的测距结果和测距误差对比Table 1 Comparison of located fault distance and locating error between two algorithms for different fault distances

根据表1，2种算法都不受故障距离的影响。文献［12］算法测距的最大相对误差为0.45%，平均相对误差为0.33%。本文算法的最大相对误差为0.25%，平均相对误差为0.175%。本文算法对不同的故障距离显示了更高的测距精度。

表2为A相单相接地故障情况下，不同过渡电阻时的测距结果和测距误差对比。

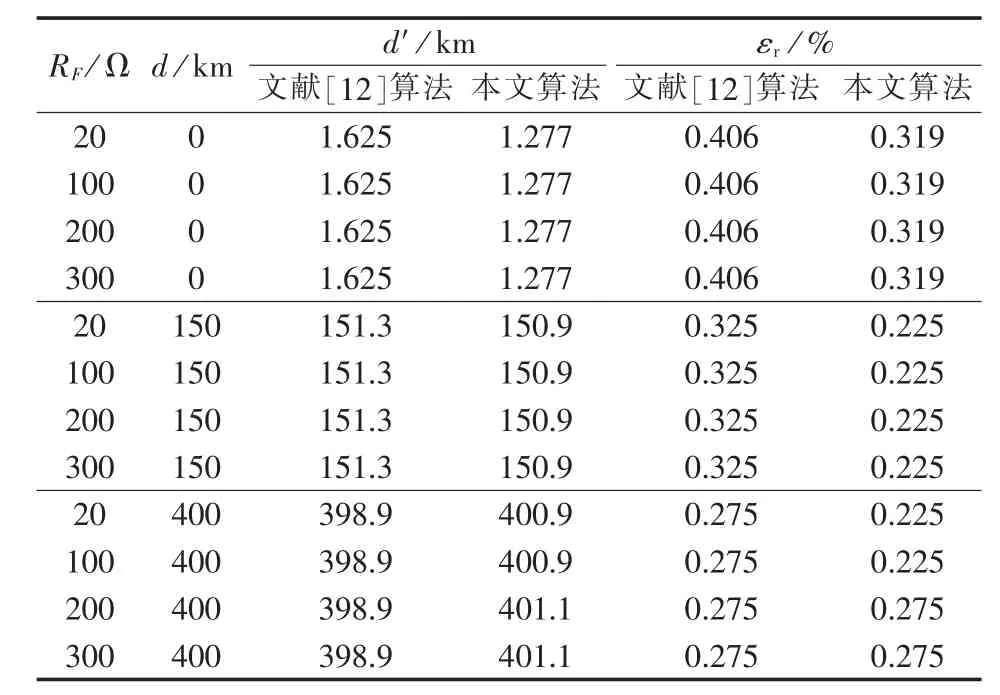
表2 不同故障电阻情况下，2种算法的测距结果和测距误差对比Table 2 Comparison of located fault distance and locating error between two algorithms for different fault resistances

根据表2，文献［12］算法的最大相对误差为0.406%，平均相对误差为0.335%。本文算法的最大相对误差为0.319%，平均相对误差为0.265%。故障电阻不影响2种算法的测距精度，并且本文算法的测距精度更高。从表2还可以看出，长线路高阻抗短路时，无论是近端还是远端，本文算法测距精度都能够满足要求。

表3为文献［12］算法与本文算法在不同故障距离、不同故障类型下的测距结果和误差对比。其中，AG表示A相单相接地；AB表示两相短路；ABG表示两相短路接地；ABC表示三相短路。

根据表3，测距精度基本不受故障距离和故障类型的影响。文献［12］算法测距的最大相对误差为0.458%，平均相对误差为0.388%。本文算法的最大相对误差为0.275%，平均相对误差为0.1596%。本文算法对不同的故障类型显示了较高的测距精度。

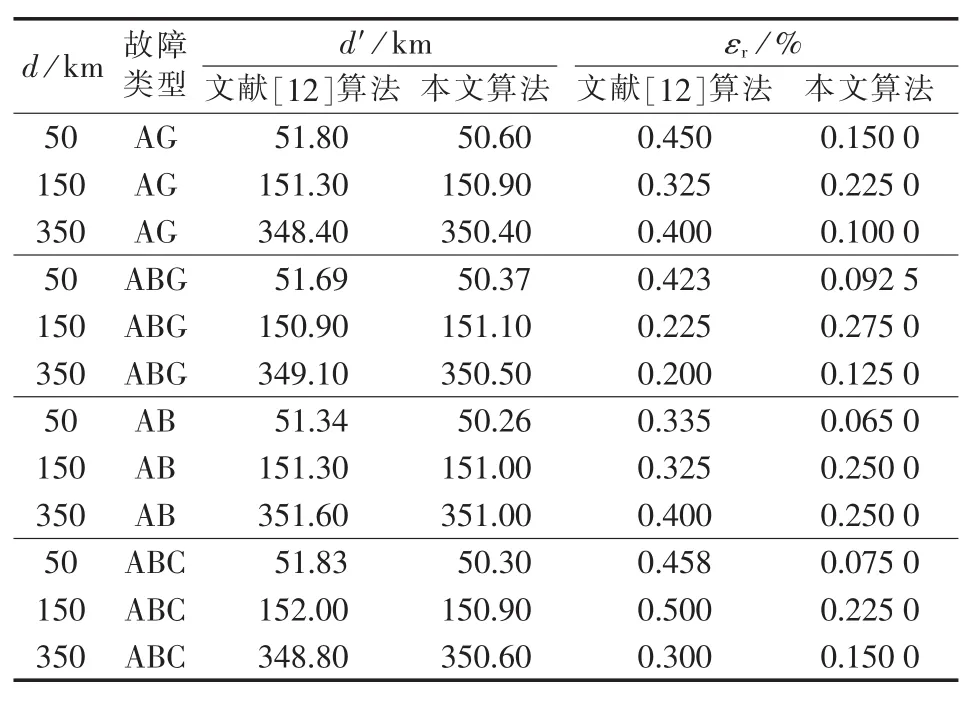
表3 不同故障类型和不同故障距离下，2种算法的测距结果和测距误差对比Table 3 Comparison of located fault distance and locating error between two algorithms for different fault types

表4为本文算法按本文实时计算线路参数方法与给定线路参数在A相接地故障时的测距结果和测距误差对比，2种方式分别记为方式Ⅰ和方式Ⅱ。

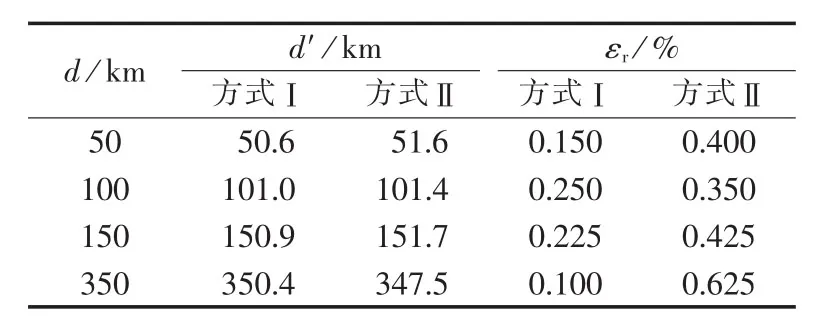
表4 2种方式下测距结果和测距误差的对比Table 4 Comparison of located fault distance and locating error between two algorithms

根据表4，按本文计算线路参数的方法进行故障测距，平均测距相对误差由0.45%减小为0.1813%，提高了测距精度，也能够反映系统运行方式的变化，证明了本文实时计算线路参数方法的正确性和可靠性。

表5为不同线路长度下A相单相接地故障时的测距结果和误差对比。

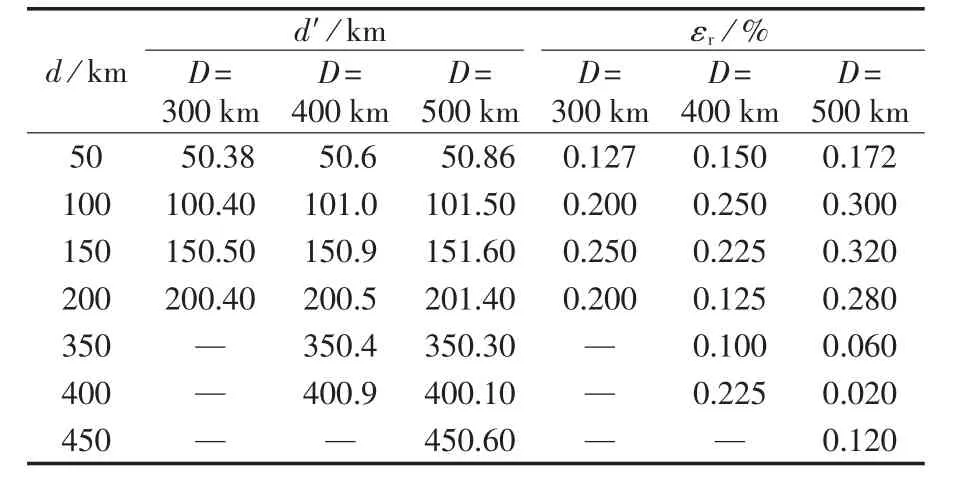
表5 不同线路长度下的测距结果和测距误差对比Table 5 Comparison of located fault distance and locating error between two algorithms for different line lengths

根据表5，在不同线路长度下测距的平均相对误差分别为0.13%、0.179%、0.182%。由此可以看出，测距误差虽然随着线路长度的增加呈增大趋势，但增加的步长在0.1%以下，能够在相当长的线路范围内保证测距精度满足要求。这一方面是由于本文算法在故障点两侧采用装型等值电路，使线路模型与实际模型更接近；另一方面是由于本文算法线路参数是基于线路分布参数模型实时获得并进行修正之后参与计算的，提高了测距精度。

表6为两端安装有并联电抗器的输电线路发生高阻抗短路故障时的仿真结果。

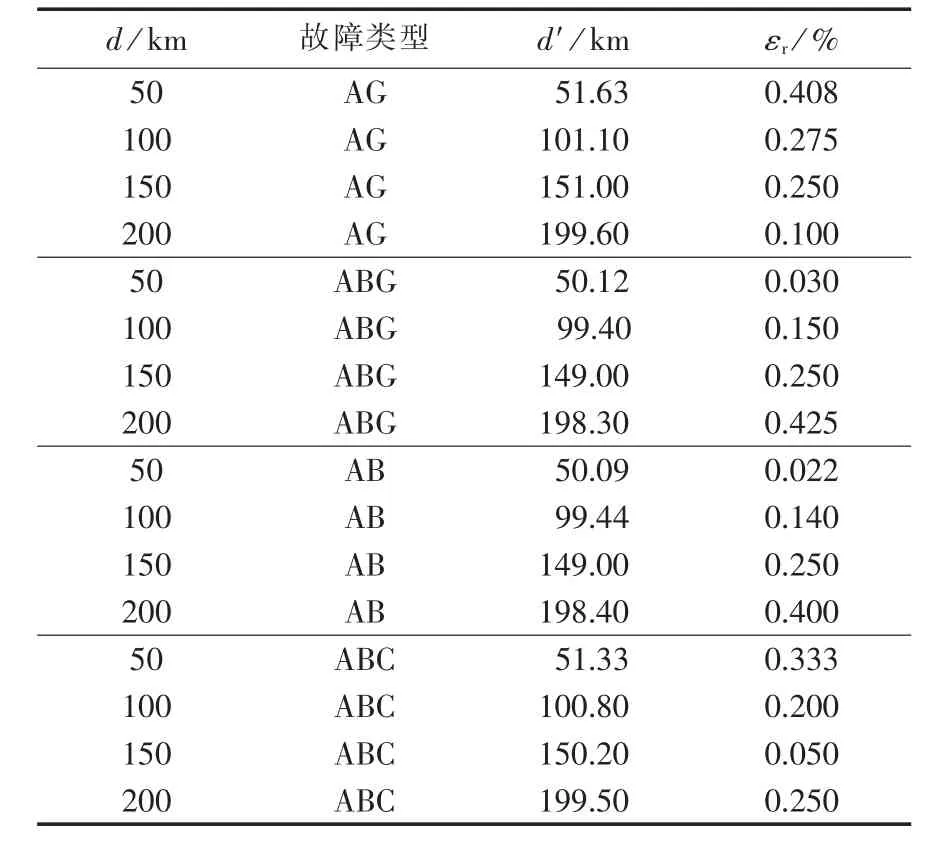
表6 线路两端安装并联电抗器时不同故障类型和不同故障距离下的测距结果和测距误差Table 6 Located fault distance and locating error of transmission line with shunt reactor at both ends for different fault types and distances

根据表6，两端安装有并联电抗器的输电线路发生高阻抗短路故障时，本文算法平均测距误差为0.221%，测距精度满足要求。测距误差有所增大的原因是算法基于工频量对电容电流进行补偿，故障状态下的大量非工频量使测距结果存在补偿误差。

6 结论

本文提出了一种基于纵向阻抗的双端量故障测距新算法，该算法具有以下优点。

a.求解故障距离时，运算量小，不需进行多次迭代和伪根识别，同时考虑了分布电容的影响，测距精度高。

b.能够在线计算出系统阻抗和线路参数，并且对线路参数进行了修正，克服了系统阻抗和线路参数变化对测距结果的影响，提高了测距精度。

c.仿真结果显示，随着线路长度的增加，测距的平均误差依次增大，分别为0.13%、0.179%、0.182%，但是测距精度仍然能够满足工程上的要求，故本文算法应该能够应用于500 km以下的长距离输电线路。而且，测距精度也不受故障类型、故障距离和故障电阻的影响，具有一定的实用价值。

d.输电线路安装并联电抗器时，本算法的测距精度能够满足要求。