考虑风速相关性的多目标电网规划

刘 学 ，李 晖 ，周 明 ，郭 飞 ，李庚银

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.国网北京经济技术研究院，北京 102209）

0 引言

风电具有随机性和波动性，大规模风电并网给电网规划中的潮流计算带来了不确定因素［1］。随着风电并网规模的增大、电网结构复杂度的增强、环保意识的提高，电网规划面临新的挑战，这已经引起国内外学者的广泛关注。文献［2］考虑环保效应，建立了风电接入的多目标电网规划模型，但没有考虑风速之间的相关性。文献［3］建立了基于动态碳排放价格的电网规划模型，但未详细讨论大规模风电对电网规划的影响。文献［4］构建了以投资成本、弃风量和切负荷量之和为目标的双层规划模型；文献［5］建立了输电网规划概率模型。这些研究关注了电网规划的经济性和环保性方面，但在表征电网结构均匀度方面和考虑风速相关性对电网规划的影响方面尚有不足。文献［6］研究了风速相关性对配电网运行特性和风电最大装机容量的影响。在输电网规划方面，对考虑风电出力随机性的概率潮流计算方法［7-9］已有大量的研究，但都是假设各风电节点的注入功率是相互独立的。事实上，地理位置相近的多个风电场之间的风速具有较强的相关性。如果不考虑这种相关性，会导致概率潮流出现较大的误差，使电网规划结果偏离实际情况。目前尚缺乏文献研究风速相关性对电网规划和环境效益的影响。因此，本文基于逆Nataf变换技术建立风速相关性模型，并将其与基于半不变量法的概率潮流结合，分析风速相关性对风电出力、网架结构及环境效益的影响，再进一步结合机会约束规划方法，考虑负荷不确定性进行多目标电网规划方法建模。

电网规划一般为多目标非线性优化问题，传统思路是将多目标转换成单目标问题进行求解［10-12］，涉及到的方法有多目标权重法、模糊集分析方法、分层优化方法、模糊评价法，这些方法可以得到一个最优解，但当涉及目标较多时，其权重选择困难，各个因素难以协调统一，在实际运用中效果不理想，因而直接进行多目标优化的进化算法得到广泛认可，比如遗传算法、粒子群算法、差分进化算法、Tabu搜索法等现代启发式算法均取得了一定效果。但在多目标优化问题的适用性上，还需要进一步研究。

考虑多风电场之间的相关性，本文构建了综合考虑经济性、电网负载均衡度以及环境效益的多目标电网规划模型。以线路的投资成本反映经济性，以线路负载率方差刻画电网负载均衡度，以最小CO2排放量表征环境效益，研究风速相关性对于各目标分量及规划方案的影响。在模型的求解中，采用计及输入相关性的半不变量法求解概率潮流，采用改进非支配排序遗传算法（NSGA-Ⅱ）求解多目标的Pareto最优解集，并以熵的序数偏好方法对最优解集进行排序，得到最终规划方案。以改进的IEEE 24节点测试系统和我国某区域实际系统进行算例分析，结果表明了所提模型和算法的合理性和有效性。

1 考虑风电相关性的概率直流潮流

概率潮流可以很好地处理风机和负荷的不确定性。在电网规划中，将线路的过负荷概率当作一个约束条件，通过控制线路的过负荷概率，来确保系统以一定的概率满足不确定信息下系统安全性的要求。假设发电机出力可调，负荷服从正态分布。

1.1 风速相关性模型

大量的风速实测数据表明，大部分地区的年平均风速分布均符合Weibull分布，故本文以两参数Weibull分布来模拟风速分布。其概率密度函数和概率分布函数表达式［7］分别如式（1）、（2）所示。

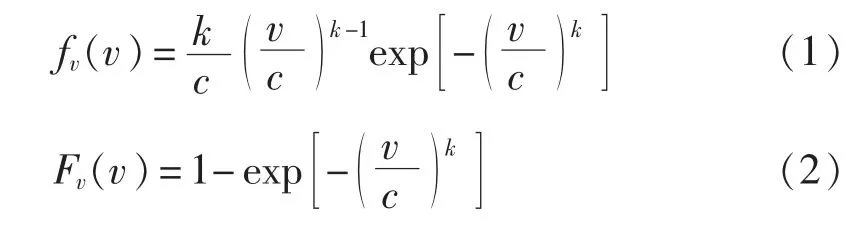
其中，v为风速；c为尺度参数；k为形状参数。

对于已知风速累积分布函数Fv（v）以及相关系数矩阵ρv的情况下，可采用逆Nataf变换生成给定相关系数的风速样本，步骤如下［13］。

步骤1利用蒙特卡洛抽样生成独立标准正态分布变量E的样本Es。

步骤2对相关系数矩阵ρv进行转换，得到相关系数矩阵ρx，其非对角元素由下式求得：

其中，D（ρvij）由 Weibull分布的等效相关系数经验计算公式求得［14］，如式（4）所示。

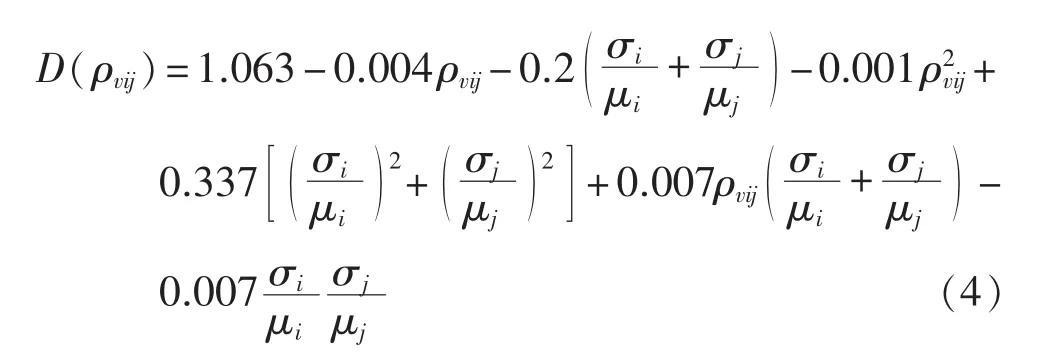
步骤3对ρx进行Cholesky分解得到下三角阵GX，通过式（5）得到相关系数矩阵为 ρx的样本 Xs。

步骤4以等概率转换原则即可生成相关系数矩阵为ρv的风速样本Vs。

其中，F-1（·）表示进行等概率转换；Φ为标准正态分布变量样本的累积密度函数。

1.2 相关性输入变量的处理

由于基于半不变量法的概率潮流要求输入变量相互独立，这就需要将相关的输入变量转换成不相关的输入变量。相关系数矩阵ρ为对称矩阵，则存在一正交矩阵B，使得相关的输入变量p转换成不相关的变量 q［7］。

变量q的相关系数矩阵Cq为单位矩阵I，结合式（7），有：

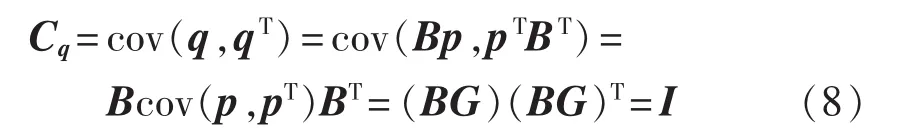
由上式可知B=G-1，代入式（7）中可得：

已知相关输入变量p的基础上，通过式（9）可将具有相关性的输入变量p表示成不相关的变量q的线性组合。

1.3 计及风速相关性的半不变量概率直流潮流

针对电网规划所需的有功功率概率分布，本文采用概率直流潮流。线路上的有功功率与节点注入有功功率之间的关系为：

其中，PL为线路潮流向量；矩阵A为节点注入功率与线路潮流之间的关系矩阵，可以由节点导纳矩阵的虚部阵B直接求得；PN为节点注入功率向量。

计及相关性的半不变量的求取，需要在独立输入变量半不变量求取的基础上，对节点注入功率的m阶半不变量进行修正。

当不同节点的注入功率p1、p2、…、pm具有相关性，并且相关系数矩阵已知时，通过式（9）可以得到不相关的变量 q1、q2、…、qm，再由式（10）将 m 个具有相关性的节点注入功率表示成不相关的变量q1、q2、…、qm的线性组合。这样输入变量不相关，便可得到支路潮流功率的各阶半不变量，进而可采用级数展开方法求取其概率分布。目前，基于半不变量计算输出变量概率分布的级数方法主要有Gram-Charlier级数、Edgeworth级数和Cornish-Fisher级数。其中Cornish-Fisher级数在计算非正态分布变量的概率分布时具有更高的精度［15］，因此，本文采用Cornish-Fisher级数计算支路潮流的概率分布。计及风速相关性的概率潮流具体流程如图1所示。

图1 考虑风速相关性的概率潮流计算流程Fig.1 Flowchart of probability power flow calculation considering wind speed correlation

2 多目标电网规划模型

2.1 多目标优化问题

多目标优化问题一般定义如下：

其中，x为解向量；F（x）为目标函数向量；n为目标函数个数；h（x）为等式约束；g（x）为不等式约束。 一般而言，多目标优化问题没有一个使所有目标函数均为最优的解，因而采用的多是Pareto最优解。Pareto最优解的评价标准由两方面组成：所获得的非劣最优解集应尽可能接近真实的Pareto前沿；所获得的Pareto最优解应沿着Pareto前沿尽可能地均匀分布。

2.2 考虑环境因素的多目标电网规划数学模型

2.2.1 目标函数

本文以单时段静态多目标电网扩展规划为例进行建模。综合考虑电网的投资运行费用、电网负载均衡度，相应的多目标函数如下。

（1）经济性指标。

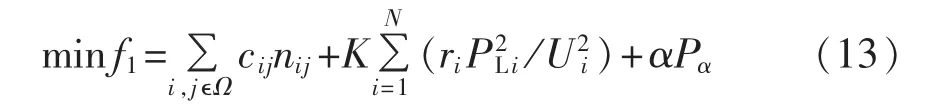
其中，cij为节点i、j之间新建线路的费用；nij为节点i、j之间的线路数量；Ω为新建线路集合；K为年网损费用系数；ri为支路i的电阻；PLi为支路i传输的有功功率；Ui为支路i的电压；α为过负荷惩罚系数；Pα为系统过负荷量。

（2）电网负载均衡度。

电网负载均衡度是指电网中输电线路负载率的分布情况。电网规划中，可能出现个别线路重载或轻载的现象，重载线路会导致电网安全性降低，规划结果滞后；轻载线路会导致电网运行的经济性较差，规划结果超前。因此，在追求经济性的同时，提高电网的安全性、避免规划方案支路中出现重载和轻载尤为重要。本文采用负载率方差作为目标函数，体现支路负荷波动限制，使线路利用率更合理。

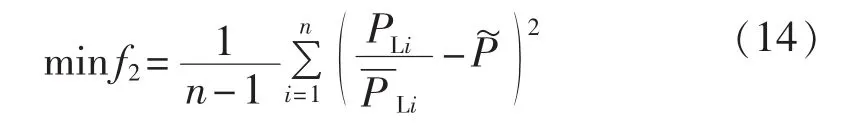
其中，PLi为支路i传输的有功功率为支路 i允许的最大传输功率为支路负载率均值。

（3）CO2排放量。

其中，Ek为第k个发电机发出单位MW功率产生的CO2量；gk为可调发电机的出力。

2.2.2 约束条件

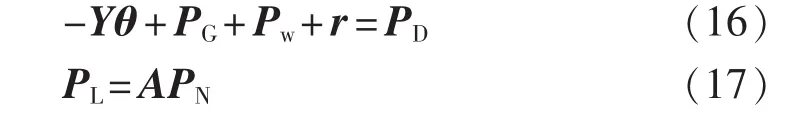
式（16）、（17）为直流潮流约束等式；式（18）为支路潮流约束；式（19）—（22）分别为发电机有功出力约束、风机有功出力约束、切负荷上限约束、可架线路走廊的架线数目约束。

3 改进 NSGA-Ⅱ

3.1 NSGA-Ⅱ及其控制参数的改进

NSGA-Ⅱ是对传统遗传算法的一种改进，是目前最流行的多目标进化算法之一，它降低了非劣排序遗传算法的复杂性，具有运行速度快、解集收敛性好的优点。算法中，变异因子F和交叉因子CR的取值对算法的搜索效率和收敛性影响很大。而NSGA-Ⅱ的进化操作机制采用传统遗传算法的交叉和变异机制，容易产生局部最优以及进化过程不稳定等问题。因此本文采用差分进化算法中的控制参数动态调整策略，增强后期局部搜索能力，从而保证了算法的收敛性，方法如下：

其中，Fmax、Fmin分别为交叉因子的上、下限；CRmax、CRmin分别为变异因子的上、下限；Kn为当前迭代次数；Kmax为最大迭代次数。

3.2 Pareto非支配排序

对于多目标优化问题，不仅要尽可能多地找到Pareto最优解，还需要使Pareto前沿在各个目标空间中均匀分布。NSGA-Ⅱ采用快速非支配排序，对种群进行快速分层，计算同一非支配等级个体的拥挤度并进行选择，使得个体能在Pareto域中均匀分布。另外，通过精英策略扩大了采样空间，保留了父代的优良个体。这样，在准Pareto最优解集中，不仅保持了种群的多样性，还使得个体均匀分布。

3.3 多属性决策方法

多目标优化问题最终得到一组Pareto最优解集，需要根据决策者偏好从Pareto最优解集中选取出一个最优折中解。目前比较常用的一种方案是逼近理想方案序数偏好的方法（TOPSIS）［16］，其目标就是使得所选择的方案与理想方案的差距最小，并且与负理想方案的差距最大。但是权重一般情况下是很难给出的。因此可以采用熵权选取方法。如果指标的信息熵越小，该指标提供的信息量越大，在综合评价中所起作用就越大，权重就应该越高。反之，熵值越大，指标权重应该越小。在信息论中，熵用来衡量不确定性的程度。当变量的不确定程度越大，熵值也就越大。

3.4 基于改进NSGA-Ⅱ的多目标电网规划求解步骤

本文对NSGA-Ⅱ进行改进，采用差分进化算法中的动态控制参数的调整策略。保留了NSGA-Ⅱ中快速非劣排序、个体拥挤度比较以及精英保留策略，使其更适用于求解多目标问题。本文求解多目标电网规划问题的步骤如图2所示。

图2 非支配排序差分进化算法的多目标电网规划流程Fig.2 Flowchart of multi-objective power grid planning based on non-dominated sorting differential evolution algorithm

4 算例分析

首先以IEEE 24节点系统为例进行计算分析。系统中节点数据、支路数据和可扩建走廊数参见文献［17］，该系统有41条支路，10个发电机节点。设定风机参数为：切入风速vci=4 m/s、额定风速vrate=10 m/s、切出风速vco=22 m/s，风电场风速期望值 Ewind=5.4 m/s，标准差 σwind=2.7 m/s。单位长度线路投资费用Cij=80万元/km，功率基准值为100 MW。风电场在节点24、9并网，每个节点并网规模为250 MW，如图3所示。发电机类型如表1所示，并且不同类型的机组具有不同的碳排放强度［17］，如表2所示。

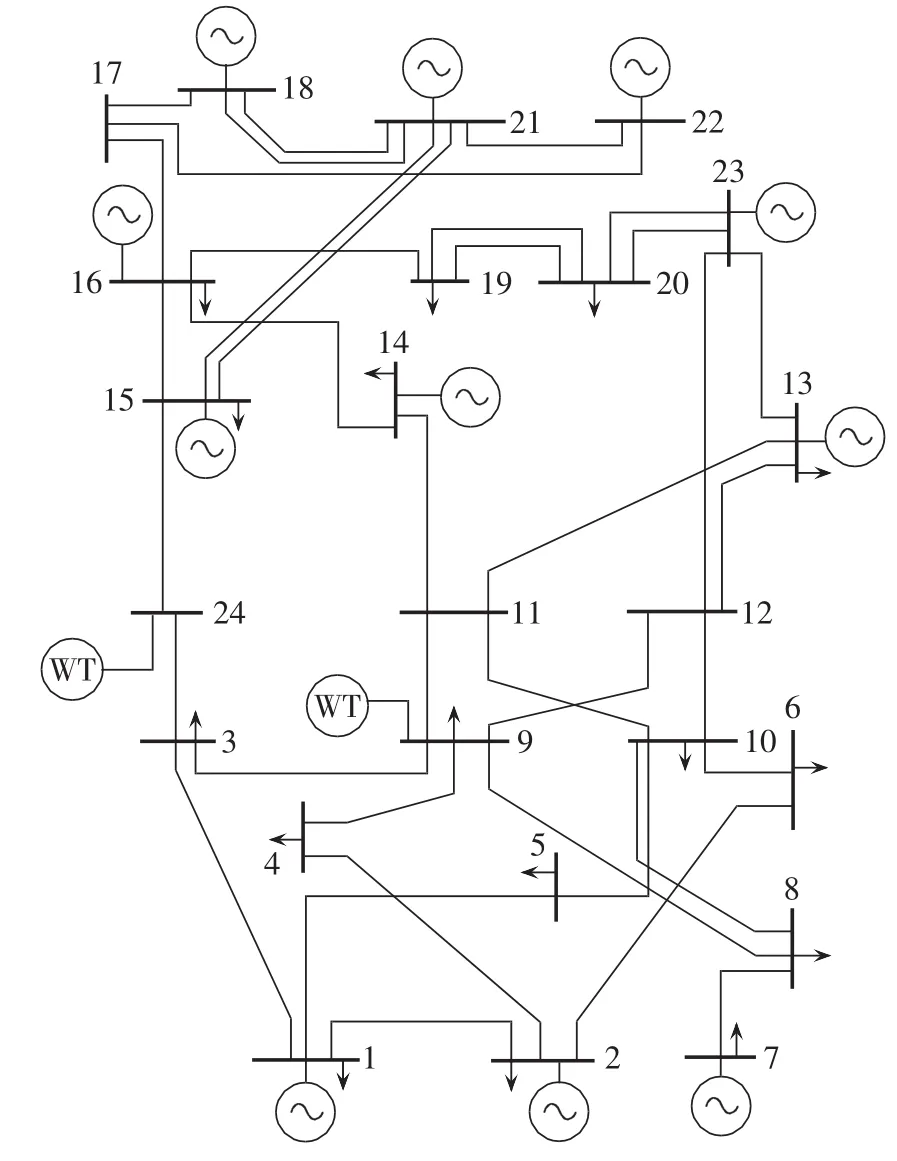
图3 IEEE 24节点风机并网系统图Fig.3 IEEE 24-bus system with grid connected wind turbines

表1 IEEE 24节点系统电源类型Table1 Power source types of IEEE 24-bus system

表2 不同机组的CO2排放强度Table 2 CO2emission intensity of different units

4.1 考虑风电相关性的概率直流潮流分析

图4为3对不同风速相关程度的两风电场总输出功率的频率分布图，图中总输出功率为标幺值。

从图中可以看出，风速相关程度越高，两风电场的总输出功率分布在零出力和最大出力的概率越大。而风速相关程度越低，两风电场的峰和谷到达时间相差越大，零出力和最大出力出现的时刻也相差越大，风电场的总输出功率“叠加”趋势不明显。

本文采用半不变量结合Cornish-Fisher级数展开的方法进行概率直流潮流计算。为了对比，选取蒙特卡洛仿真10000次，得到支路有功功率累积分布函数曲线，选取支路1-5的有功功率累积概率分布曲线为例，结果示于图5，图中支路1-5有功功率为标幺值。曲线对比表明所提方法的计算结果与蒙特卡洛法几乎一致，证明了所提方法有很高的精度。而采用半不变量法时，计算时间为0.1724 s，采用蒙特卡洛法的计算时间为91.3048 s，计算速度得到了大幅提高，提高了运算效率。

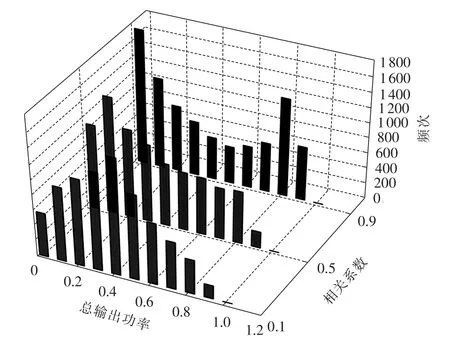
图4 不同风速相关系数下风电场总出力概率分布Fig.4 Probability distribution of total wind farm output for different wind speed correlation coefficients

图5 支路1-5有功功率分布Fig.5 Reactive power distribution of branch 1-5

4.2 考虑风电相关性的优化方案分析

4.2.1 IEEE 24节点测试系统

本文的改进NSGA-Ⅱ参数如下：种群规模NP=100，最大迭代次数Kmax=200，变异因子上限Fmax=0.8，下限Fmin=0.3，交叉因子上限CRmax=0.8，下限CRmin=0.3。

为了描述风电相关性对输电网扩展规划的影响，分别对风电场不相关以及风电场3种不同相关系数的情况进行计算，并以基于熵权的TOPSIS法进行决策，选出最优方案。计算结果如表3所示。

由表3对比可知，随着风电场相关程度越高，风电场的总输出功率分布有“叠加”的趋势，使得在零出力和最大出力的概率增大，风电的波动性越强。随着风电场相关系数的增加，为了保证系统的可靠性，新建线路数量也随之增多，这一特性在风电场并网节点24、9相邻线路尤为明显，表明风电场出力波动性给风电场并网点相邻线路带来更大的风险，需要加强建设。通过增加经济投资，提高电网的可靠性，并达到令决策者满意的水平。在电网负载均衡度方面，风电场相关系数的增加，会使得风电场出力的标准差增大，出力的波动性也愈大，线路的负载率方差也增大。表3中支路最大负载率随着风电场相关系数的增加而增加，而支路最小负载率随着风电场相关系数的增加而减小，说明风电场相关系数越高，风电场出力共同增大或减小的趋势越明显，使得线路最大负载率变高、最小负载率变低，电网负载均衡度变差。从环境层面来看，风电接入会替代相当一部分常规能源，使得CO2单位时间排放量减少，原系统碳排放量为1506.29 t/h，方案1—4减排量分别为 585.16 t/h、586.64 t/h、608.92 t/h、637.96 t/h，能够带来可观的环境效益。考虑风电相关性时，随着网架结构的增强，风电场的出力相应增加，CO2的单位时间排放量有所减少，与不考虑风电相关性时相比差值较大。因此考虑相关性下的环境因素使规划方案数据更为精确，也更贴近于实际情况。

表3 不同风速相关系数下最优规划方案Table 3 Optimal planning scheme for different wind speed correlation coefficients

4.2.2 国内某区域电网某年电网规划方案

进一步将所建模型和算法应用于我国某区域750 kV主干网某年的水平年电网扩展规划中，对其冬季大负荷方式进行验证计算。该区域电网的扩展规划基准年取为2014年，规划期内新增15个电源节点，其中节点 26（JQ）、27（QW）、29（DH）、44（HMB）为千万千瓦级风电基地，装机容量分别为2692 MW、5548 MW、5470 MW、4500 MW。采用基于正态分布的概率模型来表示负荷增长的不确定性。750 kV线路造价为258万元/km，待扩建线路最大回路数为3，算法的种群数为200，最大迭代次数为1000次。

本文采用4种方案研究风电场相关性对于电网规划的影响，方案1—4分别设定各个风电基地为不相关性、弱相关性、中相关性、强相关性，相关系数分别为 0、［0，0.2］、［0.4，0.6］、［0.8，0.95］。其中方案 3在区间［0.4，0.6］的相关系数最为贴近实际情况。各个方案最优规划结果见表4，且各个方案N-1情况下均不失负荷。可看出，方案1—3有共同的最优网架结构，但随着风电基地相关系数的提高，波动性随之提升，一定程度上影响了线路潮流的分布，电网负载率方差增大，电网负载均衡度越来越差。与实际情况最为贴近的方案3对应的网架优化方案结构图参见图6，风电基地附近线路网架均为双回750 kV线路，网架结构坚强。方案4为风电基地强相关情况，为了应对风电基地的强波动性，保证系统不失负荷以及N-1情况下不失负荷，风电基地附近网架进一步加强，相比方案3建设费用增加了16.2594亿元，其网架结构减少了44-45（HMB-JJM）的1条线路，增加了44-46（HMB-JJH）2条线路，使走廊输电容量提升，且形成环网，形成更坚强的网络结构，保证了大量风电功率的输送。各风电基地的强相关性，使风电基地出力的波动性趋于一致，相互叠加，线路最大负载率变大，最小负载率略有变小，电网的负载均衡度变差。

随着风电场相关系数的增大，支路负载率分布范围呈增大的趋势，但支路平均负载率却增长不明显，这是由于负载率高的支路基本为风电基地相邻线路，数量不多，而其余大部分线路的负载率均处于较为理想状态。以上对比说明，风电接入规模越大，风电场地理位置越集中，风电出力的波动性就越大，电网潮流也会大范围波动，成为重点加强区域。

从环境层面来看，前3种方案线路结构一致，虽然风电出力的波动性增加，但风电出力的期望值基本不变，其碳排放量相差不大。随着风电相关性进一步增强，方案4中风电场相邻的线路结构发生改变，网架更加坚强，使得风功率的送出能力增加，系统CO2的排放量大为降低。因此综合考虑风电的相关性，规划数据能够更贴近实际，为规划人员提供准确的数据基础。

从算法方面，对外部解进行分析，利用本文的改进NSGA-Ⅱ和NSGA-Ⅱ分别独立运算50次。每个子目标在每一代均会产生一个外部解。统计2种算法50次运算后得到的外部解对应的目标分量平均值，绘制进化曲线如图7所示。

表4 规划方案及指标对比Table 4 Comparison of grid planning and indexes among four schemes

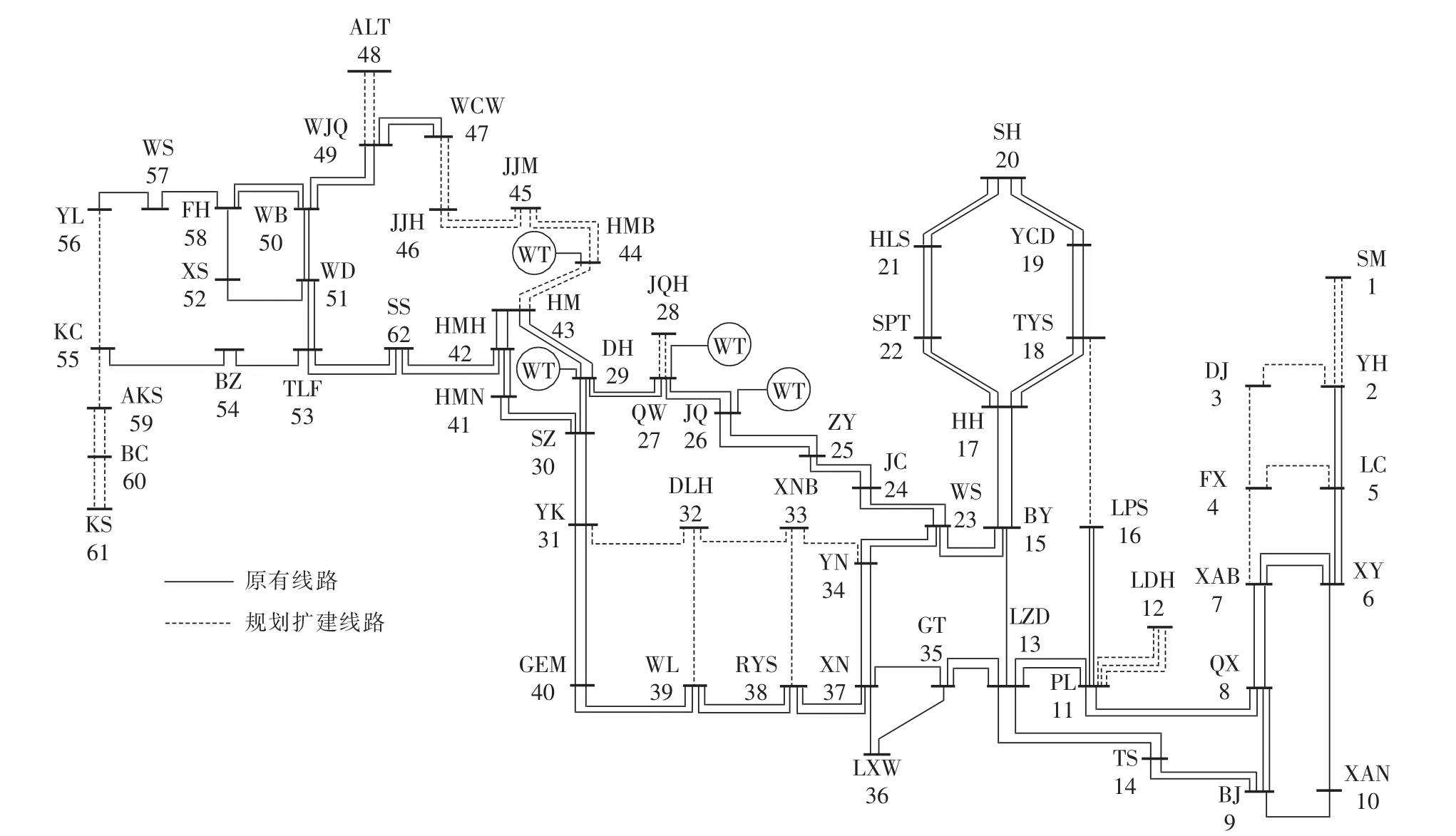
图6 方案3对应的2020年国内某地区750 kV电网方案图Fig.6 2020’750 kV grid scheme corresponding to scheme 3 for a region in China

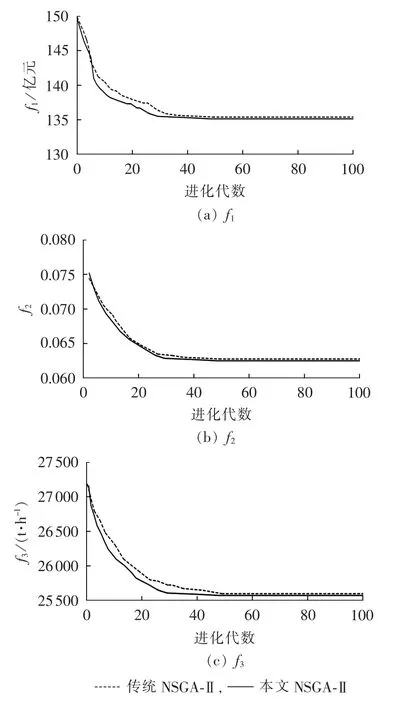
图7 不同目标函数2种算法的收敛速度Fig.7 Convergence speed of two algorithms for different objectives

从图7的对比可以看出，改进的NSGA-Ⅱ有较强的搜索能力，在5～10代以后收敛速度明显提高，并且从整体上来看，本文算法的稳定性和搜索能力都要优于传统算法，整体效果较好。

5 结论

本文建立了考虑风速相关性的半不变量法概率直流潮流计算模型；综合考虑投资经济性、电网负载均衡度、最小CO2排放量3个指标，构建了多目标电网规划模型，并给出了改进的NSGA-Ⅱ。IEEE24节点和实际算例验证表明：所给出的计及风速相关性的半不变量法概率直流潮流计算方法计算量小、计算速度快；多目标电网规划结果可以有效地反映不同风速相关系数下经济性、电网负载均衡度、环境因素三者之间的关系及变化趋势，能够从经济性、安全性以及环保多角度给出更均衡的规划方案。