基于市场的中长期电力消费需求预测

傅守强，汪莹，刘素伊，叶承晋，刘畅，刘洋，岳云力，游沛羽（.国网冀北电力有限公司经济技术研究院，北京00055；.国网北京经济技术研究院，北京0005；.浙江大学电气工程学院，浙江杭州007；.国家电力调度控制中心，北京000）

基于市场的中长期电力消费需求预测

傅守强1，汪莹2，刘素伊1，叶承晋3，刘畅4，刘洋1，岳云力1，游沛羽2
（1.国网冀北电力有限公司经济技术研究院，北京100055；2.国网北京经济技术研究院，北京100052；3.浙江大学电气工程学院，浙江杭州310027；4.国家电力调度控制中心，北京100031）

中长期电力消费需求与市场发展密切相关，目前的电力需求预测方法对市场的关注度远远不够。文中从市场着眼，建立基于宏观经济、产业结构和终端能源结构等市场因素的电力消费需求预测模型。将经济增长构成要素分为投资、消费、出口3个方面，运用向量自回归（VAR）模型表征电力消费的时间序列与经济指标时间序列的关系。采用灰色理论常见模型GM（1，1）的精确形式DGM（1，1）模型对分产业用电量进行预测。根据马尔可夫预测无后效性的特点，建立最优化模型求取预测年份的终端能源概率。采用残差均方根来反映预测模型对历史数据的拟合程度，确定各预测方法权重，进行组合预测。文中以某省电力消费数据为实例，预测该省中长期电力需求，并通过校验证明了方法的准确性。

电力需求预测；经济增长因素；产业结构；终端能源结构；VAR模型灰色理论；马尔科夫过程残差均方根

中长期电力需求预测是指未来3～5年甚至更长时间段内的预计电力消费量，是电网改造和扩建工作远景规划的重要依据[1]。综合国内外对电力系统长期负荷预测的研究，当前采用的预测技术和模型主要分为传统方法、经典方法、智能方法三大类[2]。方法不同，但大多单纯地依靠电力需求历史数据进行预测，而对经济发展、国家政策等市场因素关注度不够；个别方法考虑了市场的因素，但仅仅用单一经济指标来反映，模型过于简单粗糙，预测精度不高[3-9]。

本文将电力消费的市场影响因素分为宏观经济发展、产业结构调整、终端能源消费结构3个方面，提出了基于市场的电力消费需求预测，采用多种方法建立电力需求与这3方面市场因素的模型，并进行了组合预测。

1　基于市场的中长期电力消费需求预测模型的建立

1.1基于经济增长的VAR模型

根据经济学理论，可将经济增长构成要素分为投资、消费、出口3个方面，形成3个时间序列变量。采用向量自回归（VAR）模型[10]能较好的解决多个时间序列变量的分析预测问题。

在VAR模型基础上探究电力需求与经济三大增长因素是否具有长期均衡关系，分析经济增长各个因素对电力消费的影响机理和影响程度，进而建立电力需求的预测模型。

1.1.1单位根检验

非平稳序列需要通过单位根检验，证明其为n阶单稳序列之后，方可建立VAR模型。单位根检验的常见方法是ADF检验。具体方法是估计回归方程式：

式中，p为滞后阶数；ut为残差。a为常数项；δt为时间趋势项，这两项是否为0可以通过观察时间序列曲线是否存在偏离0的位置随机波动或具有线性趋势来判定。

该检验的零假设为H0∶η=0；备择假设为H1∶η＜0。通过检验η的估计值η赞是否不拒绝原假设，进而判断一个高阶自相关序列是否存在单位根。如果单位根全部落在单位圆内，则说明序列稳定。若序列是不平稳的，还需对其差分后进一步检验，直到拒绝原假设，来确定该序列的单整阶数。

1.1.2VAR模型

VAR（p）模型的数学表达式是：

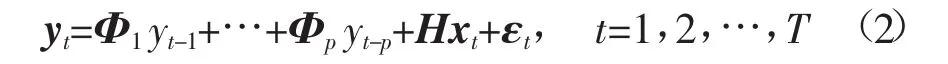
式中，yt为k维内生变量列向量；xt为d维外生变量列向量；p为滞后阶数；T为样本个数。k维矩阵Φ1，…，Φp和k×d维矩阵H是待估计的系数矩阵。εt是k维扰动列向量。

VAR模型中的一个重要问题是滞后阶数的确定。常用AIC信息准则和SC准则、LR（似然比）检验等方法确定VAR模型滞后结构。本文采用AIC信息准则和SC准则，计算方法可由下式给出：

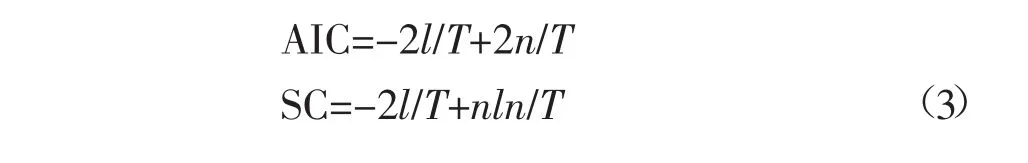
其中，n=k（d+pk）是被估计的参数总数。假定服从多元正态（高斯）分布计算对数似然值l：

AIC和SC信息准则要求它们的值越大越好[11]。

1.1.3协整检验

虽然经济变量本身是非平稳序列，但其线性组合却可能是平稳的。这种平稳的线性组合被称为协整方程且可被解释为变量之间的长期稳定的均衡关系。适用于VAR模型的协整检验是基于回归系数的Johansen协整检验[12]。协整的定义如下：

k维向量yt的分量间被成为d，b阶协整，记为yt～ CI（d，b），如果满足：1）yt～I（d），要求yt每个分量满足yit～I（d）；2）存在非零向量β，使得β′yt～I（d-b），0＜b≤d。则简称yt是协整的，向量β又称为协整向量。

对于式（2）中的VAR模型，若y1t，y2t，…，ykt都是非平稳的I（1）变量，则将式（2）经过差分变换以后，可以得到下面的式子：

由于I（1）过程经过差分变换将变成I（0）过程，即上式中的Δyt，Δyt-i（j=1，2，…，p）都是I（0）变量构成的向量，那么只要∏yt-1是I（0）的向量，即y1，t-1，y2，t-1，…，yk，t-1之间具有协整关系，就能保证Δyt是平稳过程[13]。用具有协整关系的表达式即可进行电力需求预测。

协整检验结果需要通过检验确定协整方程的数量[14]。检验的方法包括：迹统计量、最大特征值统计量以及根据MacKinnon-Haug-Michelis提出的临界值所得到的P值[15]。

上述步骤可总结流程如图1所示。

1.2基于产业结构发展的灰色理论模型

基于产业结构发展预测电力需求，需要分别对各产业的用电量情况做预测，这在实际中常常采用产值单耗法进行预测。

各产业单位增加值电耗和各产业增加值的变化数据，既含有已知信息又含有未知或非确定信息，对这样的系统进行预测，更适合采用在一定方位内变化的、与时间有关的灰色理论模型进行预测。

根据预测年产值单耗指标和各产业的国内生产总值目标，分别计算出各产业预测年的耗电量，然后与居民生活消费电量相加，便得到电力需求预测值。相应的公式为：

图1　基于经济增长的VAR模型预测流程图Fig.1　Forecasting flow chart of VAR model based on economic development

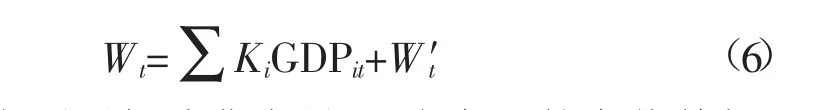
式中，Wt为预测年消费电量；Ki为产业的产值单耗；GDPit为产业预测年的产值（以不变价格计算）；W′t为预测年居民生活消费电量。

GM（1，1）模型是一种最常用的灰色预测模型。其建模的实质是确定微分方程的系数，将时间序列转化为微分方程，通过灰色微分方程可以建立抽象系统的发展模型。

深度学习应用研究（#1、#4、#5、#7聚类） 基于学科教学的深度学习研究主要集中在如何在课堂教学上开展深度学习。2015年，余胜泉通过学习原平台，创造出一门师生互教互学的课程，通过生成性教学目标、开放性教学活动等方式，激发学生参与教学的热情，提升学生的认知投入水平，促进学生深层次学习，并培养学生的创新意识[7]。张国荣在2016年运用翻转课堂教学模式开展教学实践研究，利用课堂中“教师主导作用，学生主体作用”的教学理念，调动学生的自主性，引发学生发现问题、解决问题的能力，从而促进学生深度学习[8]。

本文采用的模型

称为模型DGM（1，1），是GM（1，1）模型的离散形式[16]。DGM（1，1）模型全面符合灰色预测模型的建模机理，可以解释原GM（1，1）模型从离散形式到连续形式转变问题，是其精确形式，能有效解决中长期预测时GM（1，1）模型精度降低的问题。

方程中系数β1，β2按最小二乘法求：

式中，

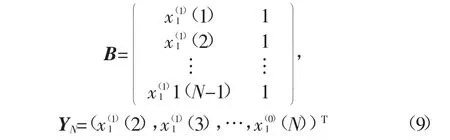
对其还原得：

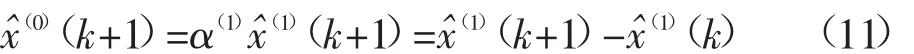
1.3基于终端能源结构的马尔科夫过程模型

1.3.1马尔可夫过程

设随机过程{X（t），t∈T}的状态空间为I。如果对时间t的任意n个数值t1，t2，…，tn，n≥3，ti∈T，在条件X（ti）=xi，xi∈I，i=1，2，…，n-1下，X（tn）的条件分布函数与在条件X（tn-1）=xn-1下X（tn）的相等，即：

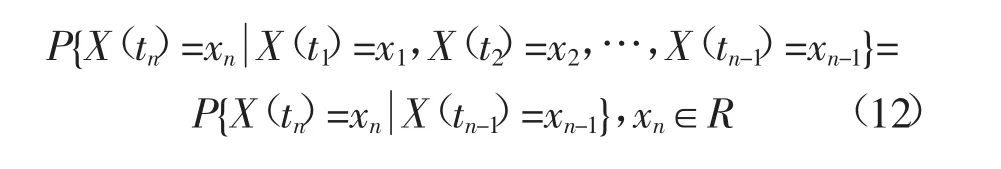
则称过程{X（t），t∈T}具有马尔可夫性或无后效性，并称此过程为马尔科夫过程。

1.3.2转移概率矩阵

马尔科夫过程可用条件概率来描述。为了方便，将当前时刻的状态记为xi，下一时刻的状态记为xj，则条件概率的公式可写为：

式中，Pij是过程从状态xi到状态xj的转移概率。如果在一次状态转移中转移概率与t时刻无关，且为一常数，即：

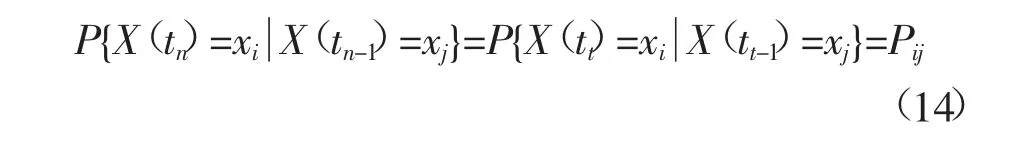
则称此马尔科夫过程为时间齐次的。在能源结构的研究中，只涉及离散的齐次马尔科夫过程。由转移概率组成的矩阵P（m，m+n）=（Pij（m，m+n））称为马氏链的转移概率矩阵[18]。由于在时刻从任何一个状态xm出发，到另一状态xm+n，路径必然经过x1，x2，…，xn中的一个或若干个，所以：

即转移概率矩阵的每一行元素之和等于1。当转移概率的步长为1时，称转移概率矩阵为一步转移概率矩阵，记为：

写成递推关系为：

用马尔可夫预测模型来预测能源结构未来状态的具体步骤为：确定系统状态；确定一步转移概率矩阵；利用公式求解某一状态下的概率；求解平衡状态的概率，对预测结构进行分析。在马尔可夫预测模型中，关键是一步转移矩阵的确定。

设S（t）=（pt（1），pt（2），…，pt（n））是时刻t系统在n个状态下的概率向量t=1，2，…，m，设一步状态转移概率矩阵为P=（pij）n×n。实际上由于客观环境的变化，相邻时刻的一步转移概率矩阵并不完全相同，因此与S（t）P 之间总存在误差。为了获得最精确的一步转移概率矩阵，本文采用最优化的思想，即在m个时刻中要使实际状态的概率向量与理论计算的状态概率向量的误差平方和达到最小为准则，建立如下最优化模型：

此问题可转化为二次规划的标准形式，可利用二次规划优化方法求解。

2　基于残差均方根的组合预测模型

为综合基于宏观经济增长、基于产业结构发展、基于终端能源结构3个单项预测法，将各方法预测结果选取适当的权重进行加权平均进行组合预测。组合预测最重要的问题是确定各种单项预测法权重{li}，i=1，2，…，n。本文采用残差均方根来反映预测模型对历史数据的拟合程度。第i种预测方法的残差Si可表示为：

式中，Xij为采用第i种预测方法得到的第j年的预测数据；xj为第j年的实际数据；m为历史数据的总年份。为避免人为协调目标时产生的主观性差异，采用基于残差均方根的客观赋权方法。设序列{Si}，i= 1，2，…，n表示每种预测方法的残差均方根，则第i种预测方法的权重为：

在确定权重之后，组合预测在第j时刻（j=m+1，m+2，…，M）的预测值，可表示为：

采用残差均方根法既可以确定各预测模型的权重，又可以考量模型对历史数据拟合的准确度。

3　实例分析

本文以中国某省份1995—2012年的电力消费及相关市场因素数据作为历史数据，预测2013—2020年电力需求，并以2013、2014年的实际数据校验预测精度。相关数据取自该省统计年鉴。

3.1基于经济增长的预测

用全社会用电量代表电力需求，经济增长的三大因素——投资、消费、净出口则分别用全社会固定资产投资额、社会消费品零售总额与净出口额这三个指标表征，样本期间均为1995—2012年。为消除原始数据的异方差性，取这些数据的增长率分析。

使用ADF检验法进行单位根检验，根据所得根落在复平面单位圆内外的情况判断序列的稳定性。结果如图2所示。

图2　AR特征多项式单位根的分布情况Fig.2　Distribution of unit root of the AR characteristic polynomial

检验结果表明：当滞后阶数为一阶时，特征多项式的根都落在单位圆内，满足建立VAR模型的要求。因为进行协整检验时对数据进行了差分变换，所以协整检验模型的滞后阶数为VAR模型滞后阶数减1[11]。利用迹统计量和最大特征值法做协整检验。两种方法得出的结果均表明：假设无协整方程的概率小于5%，故全社会用电量和全社会固定资产投资额、社会消费品零售总额、净出口额数据序列存在协整关系，协整关系式即可以用作预测方程。

根据该省社会经济发展规划，预估2013—2020年三个经济表征指标增长率，进而得到全社会用电量增长率。电力需求预测值如表1所示。

表1　某省电力消费需求预测值Tab.1　Electricity requirement forecasting of one province亿kW·h

3.2基于产业结构发展的预测

本节应用产值单耗法时统一把该省各年GDP值归算为以同一年为基准的实际GDP值。根据1995— 2012年各产业消费电量，结合归算GDP值计算得到该省一、二、三产业单位产值电耗统计数据。对各项序列指标建立离散灰色预测DGM（1，1）模型，得到2013—2020年各产业的单位产值电耗预测值。结合社会经济规划中各产业的增加值预测值，与产值单耗相乘即为各产业预测用电量。

为了保持方法的一致性，对于居民的电力需求仍采用离散灰色预测模型。结合各产业用电量可得全社会电力需求的预测结果如表2所示。

表2　某省电力消费需求预测值Tab.2　Electricity requirement forecasting of one province亿kW·h

3.3基于终端能源结构的预测

由马尔科夫过程的定义可得：2013—2020年终端能源结构分别为：S（16）P，S（16）P2，…，S（16）P9。将S（16）和P代入求得该省终端能源消费结构见表3。

分析历史数据，该省单位能耗按着相对均匀的下降速度，则根据“十二五”期间单位能耗降低18%的总体目标，平均每年单位能耗下降3.6%。设“十三五”期间产值单耗仍按照此速度下降。按照该省社会经济发展规划中确定的年均7%增长速度可推算出2013年至2020年GDP预测值，结合单位产值能耗预测值可得预测期内逐年总能耗数据。该省能源结构一直非常稳定，终端能耗在总能耗中所占比例保持在66.125%±1.085%区间内。设定预测期内该省终端能源消费量占全社会能源消费总量的比重为66.125%。标准煤和电量的换算比为1.229 t/万kW·h。

表3　某省能源的终端占有率预测值Tab.3　Occupancy rate forecasting for main sorts ofenergy end-use of one province

3.4组合预测

由预测模型得到3种方法对历史数据的拟合，采用残差均方根法确定各方法权重，得到组成预测法对历史数据的拟合。比较各预测方法误差如表5所示。

表4　基于终端能源结构法预测结果Tab.4　Electricity requirement forecasting based on energy end-use structure

表5　各预测方法误差Tab.5　Error of each forecasting methods

经组合模型，预测误差大幅缩小。可见组合预测是提高预测方法精度、增强预测方法适用性的有效途径。得2013—2020年间该省电力消费需求预测结果如表6所示。

表6　某省电力消费需求预测Tab.6　Electricity requirement forecasting of one province亿kW·h

该省2013、2014年实际电力消费量分别为3 453、3 506亿kW·h，预测值与实际值的误差分别为0.53%、2.84%。本预测方法在对电力消费需求进行中远期预测时具有误差小、精度高的优点。

4　结论

中长期电力需求与市场关系密切，在预测的过程中要给予高度重视。本文做了以下几方面工作：

1）建立了基于市场的负荷预测数学模型，从宏观经济、产业结构、终端能源结构3个维度多种方法对电力消费需求预测进行研究。

2）通过校验历史数据，采用残差均方根法确定各预测模型的权重，进行组合预测，提高精度。

3）以某省实际数据为例，预测2013—2020年电力需求，并对比2013、2014年实际值，验证精确性。

本文提出的模型对中长期电力消费需求预测具有普遍借鉴意义，可作为参考加以推广。在今后的研究中，应更全面考量影响电力需求的各种市场因素，明确相关变量的选取方式，并提高对经济指标分析预测的科学性。

[1]KANDIL M S，EL-DEBEIKY S M，HASANIEN N E. Overview and comparison of long-term forecasting techniques for a fast developing utility:part I[J].Electric Power Systems Research，2001，58（1）:11-17.

[2]卢建昌，赵磊，牛东晓，等.电力负荷预测技术及其应用[M].北京:中国电力出版社，2009.

[3]毛李帆，江岳春，龙瑞华，等.基于偏最小二乘回归分析的中长期电力负荷预测[J].电网技术，2008（19）:71-77. MAO Lifan，JIANG Yuechun，LONG Ruihua，et al.Medium-and long-term load forecasting based on partial least squares regression analysis[J].Power System Technology，2008，32（19）:71-77（in Chinese）.

[4]康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨[J].电力系统自动化，2004（17）:1-11. KANG Chongqing，XIA Qing，ZHANG Boming.Review of power system load forecasting and its development[J]. Automation of Electric Power Systems，2004，28（17）:1-11（in Chinese）.

[5]朱凤娟，王主丁，陆俭，等.考虑小区发展不均衡的空间负荷预测分类分区法[J].电力系统自动化，2012（12）:41-48. ZHU Fengjuan，WANG Zhuding，LU Jian，et al.Disequilibrium development areas based classification and subarea method for spatial load forecasting[J].Automation of Electric Power Systems，2012，36（12）:41-48（in Chinese）.

[6]周德强.改进的灰色Verhulst模型在中长期负荷预测中的应用[J].电网技术，2009（18）:124-127. ZHOU Deqiang.Application of improved gray verhulst model in middle and long term load forecasting[J].Power System Technology，2009，33（18）:124-127（in Chinese）.

[7]周湶，任海军，李健，等.层次结构下的中长期电力负荷变权组合预测方法[J].中国电机工程学报，2010（16）:47-52. ZHOU Quan，REN Haijun，LI Jian，et al.Variable weight combination method for mid-long term power load forecasting based on hierarchical structure[J].Proceedings of the CSEE，2010，30（16）:47-52（in Chinese）.

[8]龙瑞华，毛弋，毛李帆，等.基于诱导有序加权平均算子和马尔可夫链的中长期电力负荷组合预测模型[J].电网技术，2010（3）:150-156. LONG Ruihua，MAO Yi，MAO Lifan，et al.A combination model for medium-and long-term load forecasting based on induced ordered weighted averaging operator and markov Chain[J].Power System Technology，2010，34（3）: 150-156（in Chinese）.

[9]SOYTAS U，SARI R.Energy consumption and GDP: causality relationship in G-7 countries and emerging markets[J].Energy Economics，2003，25（1）:33-37.

[10]高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社，2009:568.

[11]钟志威，雷钦礼.Johansen和Juselius协整检验应注意的几个问题[J].统计与信息论坛，2008（10）:80-85. ZHONG Zhiwei，LEI Qinli.Some notes on johansen and juselius cointegration test[J].Statistics and Information Forum，2008，23（10）:80-85（in Chinese）.

[12]HERRERIAS M J，JOYEUX R，GIRARDIN E.Shortand long-run causality between energy consumption and economic growth:evidence across regions in China[J]. Applied Energy，2013，112（0）:1483-1492.

[13]赵会茹，杨璐，李春杰，等.基于协整理论和误差修正模型的电网投资需求预测研究[J].电网技术，2011（9）: 193-198. ZHAO Huiru，YANG Lu，LI Chunjie，et al.Research on prediction to investment demand of power gridBased on co-integration theory and error correction model[J].Power System Technology，2011，35（9）:193-198（in Chinese）.

[14]ENDERS W.Applied econometric time series[M].John Wiley&Sons，2008.

[15]OUéDRAOGO I M.Electricity consumption and economic growth in burkina faso:a cointegration analysis[J].Energy Economics，2010，32（3）:524-531.

[16]谢乃明，刘思峰.离散GM（1，1）模型与灰色预测模型建模机理[J].系统工程理论与实践，2005（1）:93-99. XIE Naiming，LIU Sifeng.Discrete GM（1，1）and mechanism of grey forecasting model[J].System Engineering-Theory&Practice，2005（1）:93-99（in Chinese）.

[17]刘殿海，杨勇平，杨昆，等.基于马尔科夫链的能源结构与污染物排放预测模型及其应用[J].中国电力，2006（3）:8-13. LIU Dianhai，YANG Yongping，YANG Kun，et al.Forecasting model and its application of energy structure andpollutant emission based on markov Chain[J].Electric Power，2006，39（3）:8-13（in Chinese）.

[18]黄银华，彭建春，李常春，等.马尔科夫理论在中长期负荷预测中的应用[J].电力系统及其自动化学报，2011（5）:131-136. HUANG Yinhua，PENG Jianchun，LI Changchun，et al. Application of markov theory in mid-long term load forecasting[J].Proceedingsof the CSU-EPSA，2011，23（5）: 131-136（in Chinese）.

（编辑黄晶）

Forecasting Medium and Long Term Electricity Requirement Based on Market

FU Shouqiang1，WANG Ying2，LIU Suyi1，YE Chengjin3，LIU Chang4，LIU Yang1，YUE Yunli1，YOU Peiyu2
（1.Economic Research Institute，State Grid Jibei Electric Power Company Limited，Beijing 100055，China；2.State Power Economic Research Institute，Beijing 100052，China；3.College of Electrical Engineering，Zhejiang University，Hangzhou 310027，Zhejiang，China；4.National Electric Power Dispatching and Control Center，Beijing 100031，China）

The medium and long term electricity consumption has a close relationship with the market development.The existing forecasting methods for electricity requirement，however，pay little attention to the market.With focus on the market，this paper establishes forecasting models based on macro economy，industry structure and energy end-use structure.Economy development is characterized by investment，consumption and export.The Vector Autoregression（VAR）model is employed to certify whether there is a long term cointegration between electricity requirement and economy indexes.This paper applies Grey theory to predict each industry separately.The DGM（1，1）model，which is the precise form，is used instead of the common model GM（1，1）.The Markov Prediction is suitable for the energy end-use structure.The paper sets up the optimization model and obtains energy probability. This article applies residual root mean square method to confirm the weight of each model.According to the electricity requirement of one province，codes are written to predict electricity requirement during the period of 2012 to 2020.And the real data are compared to certify the accuracy of the whole model.

electricity requirement forecasting；elements of economy development；industry structure；energy end-use structure；VAR model；Grey theory；Markov process；root mean square residual

1674-3814（2015）07-0074-07中图分类号：TM714

A

2014-12-15。

傅守强（1986—），男，硕士研究生，研究方向为电力系统评估、规划，电力市场与电力经济和电气设计；

汪莹（1990—），女，硕士研究生，研究方向为电网规划、电力经济和无功优化；

刘素伊（1979—），女，硕士研究生，副高级工程师，研究方向为输变电工程设计、技术经济；

叶承晋（1987—），男，博士研究生，研究方向为新能源发电系统、短路电流、电力系统优化；

刘畅（1988—），男，硕士研究生，研究方向为电力系统规划、电力系统调度；

刘洋（1989—），女，硕士研究生，研究方向为电力经济与企业管理；

岳云力（1987—），男，硕士研究生，研究方向为输电网规划；

游沛羽（1987—），男，硕士研究生，研究方向为输电网规划。