自动重合闸重合于永久性故障对电力系统暂态稳定的影响

白宪庆，刘劭玮，李宝昕（.辽河油田公司，辽宁盘锦400；.重庆大学，重庆400044；.国网陕西省电力公司经济技术研究院，陕西西安70065）

自动重合闸重合于永久性故障对电力系统暂态稳定的影响

白宪庆1，刘劭玮2，李宝昕3
（1.辽河油田公司，辽宁盘锦124010；2.重庆大学，重庆400044；3.国网陕西省电力公司经济技术研究院，陕西西安710065）

在电力系统网络暂态能量函数的基础上，根据暂态能量在网络中的分布与系统稳定性之间的关系，提出了永久性故障重合闸优化时间范围。通过对多机系统的仿真表明，在该时间范围重合闸可以改善电力系统暂态稳定性。

暂态稳定；永久性故障；重合闸；暂态能量

现场自动重合闸多采用继电保护跳闸切除故障后，延时一段固定的时间，再次重合断路器的方法。若是瞬时性故障，重合成功，系统进入新的正常运行状态。若重合于永久性故障对系统的暂态稳定会构成很大的威胁。如果能够采用某些切实可行而又行之有效的措施，使得即使重合于永久性故障，也不会加剧第一次故障造成的系统摇摆，最好还能对其有一定的阻尼作用，这样就会变不利为有利，从而更大程度地发挥重合闸的作用。文献[1]通过对单机无穷大系统的分析指出，在最佳时刻重合于永久性故障，不但不会引起系统失稳，反而会阻尼系统的振荡。而对于在故障后回摆中失稳的系统，在最佳时刻重合于永久性故障还可能保持系统稳定。文献[2-3]通过理论分析表明，无论是瞬时性还是永久性故障，都存在阻尼系统摇摆的重合时机，在这个时机重合不仅不会加剧摇摆，反而可以有效地阻尼系统的摇摆。文献[4]从理论上分析了重合闸对系统稳定性的影响，指出系统运行方式和接线方式经常变化，重合闸的最佳时刻也是变化的。文献[5]建立了分析重合闸时刻对电力系统稳定性影响的数学模型，使用能量函数导出瞬时性故障与永久性故障的最佳重合条件。文献[6-8]建立了多机系统以惯性中心为参考的暂态能量函数，根据瞬时性和永久性故障的不同给出了最佳重合的系统能量函数表达式，但在实际的电力系统中，难以实时采集到全系统的数据，能量函数的计算及在线分析十分困难。

本文基于多机系统的网络暂态能量函数[9]，根据电力系统的暂态能量变化特点，结合暂态能量在网络中的分布与系统稳定性的关系，从系统局部能量出发，针对永久性故障，分析了不同时间重合闸对电力系统稳定性的影响，提出了在优化时间范围重合闸可以改善电力系统暂态稳定性抑制系统振荡。

1　网络暂态能量函数

多机系统的网络暂态能量函数是在保留输电网络拓扑结构基础上推导出来的。如果某系统中有m台发电机，l0个支路，n0个母线节点，则网络中有n0－m个负荷节点。如果在原网络上增加代表发电机内电势的虚构节点，连接于发电机的内电抗，则形成系统的增广网络，则增广网络有n=m+n0个节点，l= m+l0个支路。

如果发电机采用经典模型，忽略调节器的作用，考虑负荷的频率特性，即：

式中：PDi为节点i的负荷；P0Di为节点i的负荷稳态初始值；Di为负荷频率调节效应系数；ωi为节点i的频率。

则系统的网络暂态能量函数可表示为系统动能与系统势能两部分之和，即

系统的动能表示为

式中：Mi为发电机的转动惯量；ωi为发电机的角速度。

系统的势能表示为

对于网络中任意一支路或割集k的暂态势能表示为

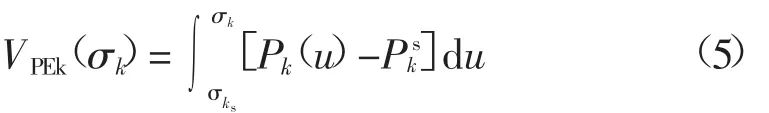
式中：σk为支路或割集k两端相角差；σks为支路或割集k相对于故障后的稳定平衡点的两端相角差；Pk（σk）为支路或割集k的有功功率；Psk为支路或割集k相对于故障后的稳定平衡点的有功功率。

若以支路或割集两端相角差变化轨迹的任意点σ0为参考点，则网络中任意一支路或割集k的暂态势能表示为

式（2）、（3）和式（4）表明，系统的暂态能量由系统的动能和势能两部分组成，其中，系统的动能为全系统各单台发电机动能总和，系统的势能可表示为增广网络中所有支路的势能总和。不论在故障结束后网络结构是否变化，以及系统是否稳定，全系统总的暂态能量（动能和势能之和）沿故障后轨迹保持守恒。系统的动能和势能进行等量交换，系统的势能分布于增广网络中的所有支路。式（5）、（6）表明：支路的暂态势能VPEk（σk）不仅与t时刻的σk值以及t时刻以前的σk值变化状态有关，而且还与参考点处的暂态势能的值有关。

暂态能量在系统中某一环节的分布与系统的暂态稳定性有着密切的关系，当系统遭受故障冲击时，将被注入新的暂态能量，并分布于包括发电机及网络的整个系统中。故障冲击越严重，被注入新的暂态能量就越多。若新注入的暂态能量能被系统网络完全吸收，则系统保持稳定。否则，由于系统中某一局部能量的过分集中将导致系统在相应于网络中的某一割集上失去稳定，这个被“撕裂”的割集被称为临界割集[9]。暂态能量在网络中某一局部的严重冲击是导致系统失稳的重要原因，该网络局部的脆弱性对系统的稳定性十分关键。如果采取有效的方法提高该网络局部的强壮性，将能很大程度上改善系统的暂态稳定性。

2　永久性故障不同时间重合闸对电力系统稳定性的影响分析

以图1所示的系统为例，如果在子系统A、B间双回联络线之一l1发生永久性故障，故障线路l1第一次切除时间为tc，然后在tc′时刻重合该线路，在ts′时刻再次切除该线路。在这一故障序列中，该割集共经历3种不同的状态，图2（a）、2（b）、2（c）为永久性故障时对应于不同的重合闸动作时间的包含故障线路的脆弱割集有功功率随两端相角差的变化曲线。其中：1-6分别为1-σmin；2-σo；3-σc；4-σ′c；5-σ′s；6-σmax；Pk1（σk）、Pk2（σk）、Pk3（σk）分别为故障前、故障后、故障线路切除后割集断面的有功功率相对于割集间两端相角差的变化曲线，Psk为故障线路切除后割集断面的有功功率相对于割集间两端相角差的变化曲线。

割集在故障前稳定运行在曲线Pk1（σk）上，σko处，故障后运行于曲线Pk2（σk）上，σc处故障切除，此时该割集承担的暂态能量的大小为A。故障线路切除后运行于曲线Pk3（σk）上，至σkmax处，承担的暂态能量值为［B1+B2］。运行点沿Pk3（σk）回摆至σkmin处，承担的暂态能量值C。运行点沿Pk3（σk）向点σko′方向回摆，进入第二个振荡周期。由于振荡过程总有能量损耗，如果故障支路没有电气操作且割集两端相角差未被“撕裂”，则割集将沿曲线Pk3（σk）往复振荡，最后停留在σko′点上运行。

图1　网络中临界割集的示意图Fig.1　The diagrammatic sketch of critical cutest in the network

图2　不同重合闸时间割集功角特性曲线Fig.2　The curve of rotor angle of cutest at different recosing time

如图2（a）所示，在割集两端相角差达到最大值σkmax后开始减小至新的稳定平衡点σko′的过程中重合于永久性故障。设点σks′对应的时刻为永久性故障最佳重合闸时刻，选择σko′再次切除故障，在σkmax→σko′变化过程中割集所承担的暂态能量值分别用B2与D表示。

点σks′为参考点，即

根据式（6）得包含故障线路的脆弱割集所承担的暂态势能B2与D分别为：

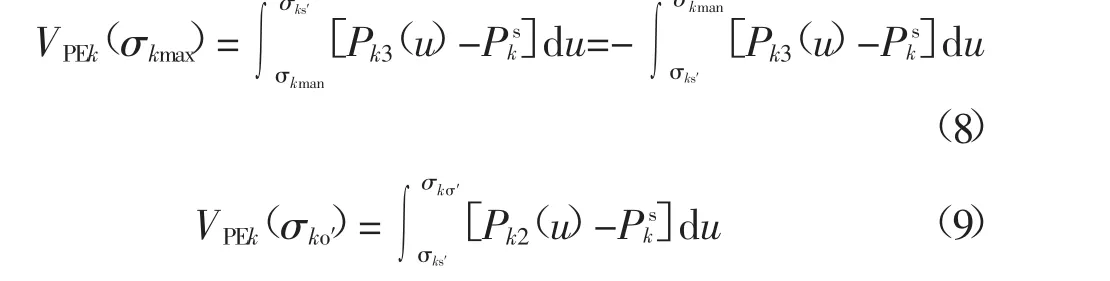
该割集最后一次操作后所受到的暂态势能表示为

如果控制重合闸时间使得包含故障线路的脆弱割集所承担的暂态势能B2与D相等，则该割集最后一次操作后所受到的暂态势能冲击为零。所求的重合闸时刻ts′为永久性故障最佳重合闸时间。此法只能离线计算。使式（10）所示的网络暂态能量函数为零值的时刻是重复出现的，因此最佳重合闸时刻不是唯一的。

图2（b）所示为故障条件不变，故障第二次持续时间不变条件下，如果在σk达到σkmin处，开始进入第二次振荡过程中，在点σko′再次重合于永久性故障，故障后沿Pk（2σk）运行，该割集新的注入暂态能量为D。此时该割集总的暂态能量为［A+D］。增加了暂态能量对该割集的冲击，恶化系统的暂态稳定水平。在此情况下再次重合故障跳闸后系统是否稳定很大程度上取决于再次切除故障的速度。

如图2（c）所示，在σk达到σkmax后并减小至σko′处重合于故障，在σk首次达到最小值时再次切除故障线路，则新注入的暂态能量D起阻尼作用，故障线路切除后沿Pk（3σk）运行，该割集最后一次操作后所承担的暂态势能为E。与故障切除后不重合割集承担的暂态能量［B1+B2］相比，E小于［B1+B2］，这种重合闸时间选取在改善电力系统暂态稳定性方面可达到很好的效果。

3　仿真与分析

为了验证本文提出的永久性故障情况下不同时间重合闸对电力系统稳定性有不同的影响，而在优化时间范围重合闸可以改善电力系统暂态稳定性的正确性，对NEW ENGLAND 10机39节点系统在发生永久性故障的情况下，不同重合闸时间进行仿真计算。NEW ENGLAND 10机系统见图3。

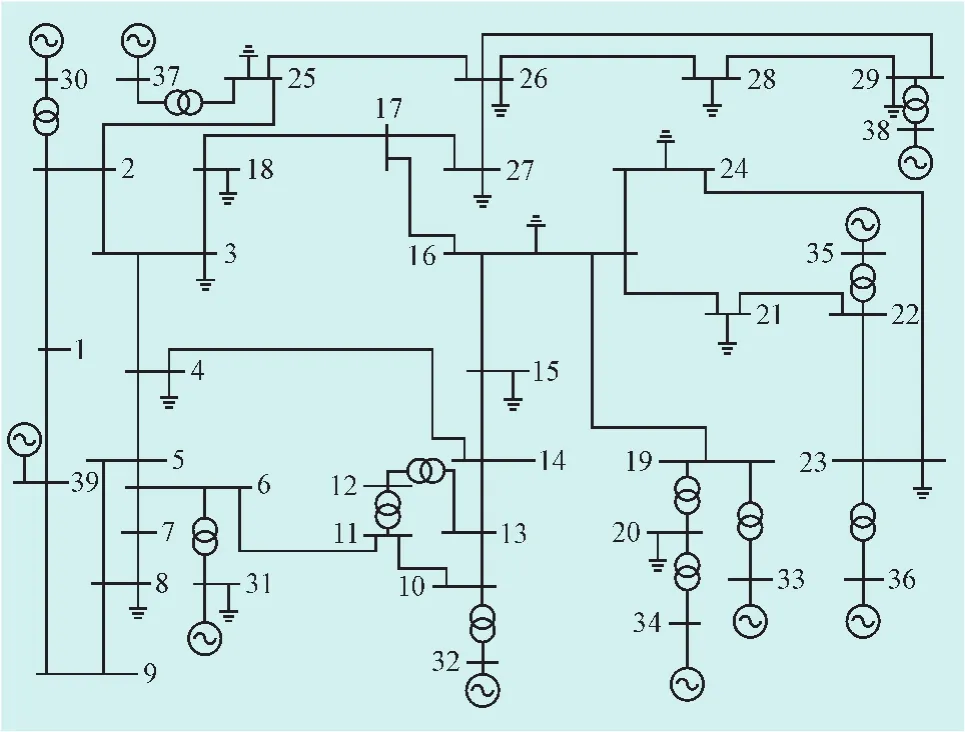
图3　NEW ENGLAND 10机系统Fig.3　NEW ENGLAND 10 Generator of power system

若三相永久性故障发生在2-1支路，0.1 s故障线路切除，则{2-1，8-9}构成网络的一个脆弱割集。经仿真计算表明，在割集{2-1，8-9}两端相角差达到最大值后开始减小至最佳重合闸时刻重合，在新的稳定平衡点再次切除故障线路，即1.84 s再次重合，1.95 s再次切除故障，割集{2-1，8-9}所承担的暂态能量最小。在故障条件不变，故障第二次持续时间不变的条件下，在割集{2-1，8-9}两端相角差回摆至最小值处，并在两端相角差增大至新的稳定平衡点再次重合永久性故障，即在3.07 s再次重合，3.18 s再次切除故障，割集{2-1，8-9}所承担的暂态能量最大。而在割集{2-1，8-9}达到新的稳定平衡点1.95 s再次重合，重合后在割集{2-1，8-9}两端相角差首次为最小值2.05 s再次切除故障，可有效减少割集承担的暂态能量。由图4不同重合闸时间割集{2-1，8-9}暂态势能分担量变化曲线可见，在1.84 s重合闸割集{2-1，8-9}承担的暂态能量最小，此时刻为最佳重合闸时间，与计算结果相符。比较在线路不重合以及重合闸时间分别整定为3.07 s、1.84 s以及1.95 s时，发电机功率、动能、相平面图变化曲线以及割集{2-1，8-9}暂态势能变化幅度，由图5—8表示。

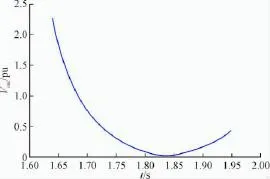
图4　不同重合闸时间割集{2-1，8-9}暂态势能分担量变化曲线Fig.4　Variation of shared potential transient energy of cutest{2-1，8-9}at different recosing time

图5　不同重合时间发电机30-39间功率变化曲线Fig.5　Generator 30-39 power curve at different recosing time

图6　不同重合时间发电机30-39间动能变化曲线Fig.6　Generator 30-39 kinetic energies curve at different recosing time

图7　不同重合时间发电机30-39间相平面图Fig.7　Generator 30-39 Angular velocity against rotor angle curve at different recosing time

由仿真结果可知，当重合闸时间分别整定为1.84 s及3.07 s时，与不重合闸相比，对系统暂态稳定性的影响截然相反，即在割集{2-1，8-9}承担的暂态能量最小时刻1.84 s重合闸显著平抑了后续摆的振荡，提高了系统的暂态稳定水平。而在割集{2-1，8-9}承担的暂态能量最大时刻3.07 s重合闸，将进一步加剧系统后继摆的振荡，恶化系统的暂态稳定性。在割集{2-1，8-9}到达新的稳定平衡点时刻1.95 s重合，可以有效平抑系统后续摆振荡，提高系统稳定性。

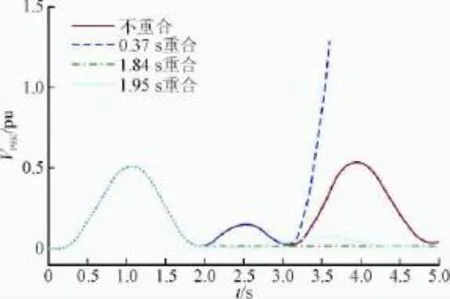
图8　不同重合时间割集{2-1，8-9}暂态势能变化曲线Fig.8　The curves of potential transient energy of cutest {1-2，8-9}at different recosing time

4　结论

通过对电力系统的暂态能量变化特点的分析，结合暂态能量在网络中的分布与系统稳定性的关系，从系统局部能量出发，验证了发生永久性故障采用不同时间重合闸对系统有不同的影响，当系统发生永久性故障并切除故障线路后，在相角差增大的过程中重合闸会加剧系统局部能量的不平衡，恶化系统的暂态稳定水平。提出存在永久性故障最佳重合闸时刻，即故障线路切除后包含故障线路的割集最后一次操作所承担的暂态势能冲击为零的时刻。此法只能离线计算。提出了重合闸优化时间范围，即永久性故障的最佳重合闸时间与割集新的稳定平衡点之间的时间范围。当系统发生永久性故障并切除故障线路后，包含故障线路的割集在两端相角差减小的过程于重合闸优化时间范围内重合，在该割集两端相角差首次为最小值再次切除故障。这种再次故障重合时间与再次切除时间相配合在改善电力系统暂态稳定性方面可达到很好的效果。

[1]王梅义，吴竞昌，蒙定中.大电网系统技术[M].2版.北京:中国电力出版社，1995:164-255.

[2]BAHBAH AMR G，GIRGIS Adly A.An investigation on the effect of line reclosing on transient stability assessment for multi-machine power systems[J].IEEE，1999，28（9）: 1082-1087.

[3]BO Z Q，AGGARWAL R K，JOHNS A T.New concept in transmission line reclosure using high-frequency fault transients[J].IEE Proc-Gener TransmDistrib，1997，144：351-356.

[4]张保会，袁越，薄志谦.最佳重合闸时间及其整定计算[J].中国电力，1995，28（2）:12-16. ZHANG Baohui，YUAN Yue，BO Zhiqian.Optimal reclosing time and its setting calculation[J].Electric Power，1995，28（2）:12-16（in Chinese）.

[5]ZHANG Baohui，LI Yinghui.The mathematical model for analysis the effects of reclosure interval time on power systemstability[C]//IEEEPowercon’98International Conference，Beijing，China，1998:1130-1134.

[6]袁宇春，张保会，钱国明.多机电力系统中重合闸最佳时刻的研究-第1部分瞬时性故障最佳重合闸时刻的研究[J].电力系统自动化，1998，22（4）:16-18. YUAN Yuchun，ZHANG Baohui，QIAN Guoming.Study on the optimal reclosing time in multi-machine power system:part one study on the optimal reclosing time at instantaneous fault[J].Automation of Electric Power Systems，1998，22（4）:16-18（in Chinese）.

[7]袁宇春，张保会，阎海山.多机电力系统中重合闸最佳时刻的研究-第2部分永久性故障最佳重合闸时刻的研究[J].电力系统自动化，1998，22（6）:46-48. YUAN Yuchun，ZHANG Baohui，YAN Haishan.Study on the optimal reclosing time in multi-machine power system: part two study on the optimal reclosing time at permanent fault[J].Automation of Electric Power Systems，1998，22（6）:46-48（in Chinese）.

[8]YUAN Yuchun，ZHANG Baohui，WU Qingfang.A method for capturing optimal reclosing time of transient fault[C]// Powercon’98，Beijing，China，1998:1138-1142.

[9]CAI Guowei，MU Gang，LIU Zhuo.The trajectory based network transient energy evaluation and its application to enhancementoftransientstability[C]//Powercon’98，Beijing，China，1998:1369-1370.

（编辑冯露）

The Influence on Automatic Reclosing on Permanent Fault on the Transient Stability of Power Systems

BAI Xianqing1，LIU Shaowei2，LI Baoxin3
（1.Liaohe Oilfield Company，Panjin 124010，Liaoning，China；2.Chongqing University，Chongqing 400044，China；3.State Grid Shaanxi Economic Research lnstitute，Xi’an 710065，Shaanxi，China）

On the basis of network transient energy function，the relationship between the distribution of transient energy in network and system stability，the reclosing time range of permanent fault was proposed in this paper.Within which time，the stability of system transient state could be improved in the simulation of multi-machine system.

transient stability；permanent fault；reclosing；transient energy

1674-3814（2015）07-0069-05中图分类号：TM762.2

A

2015-03-15。

白宪庆（1976—），女，硕士研究生，工程师，研究方向为电力系统；

刘劭玮（1994—），男，大学本科，研究方向为电力系统；

李宝昕（1987—），男，大学本科，助理工程师，研究方向为电力系统。