基于模糊隶属度的电力系统抗差估计

陈妤，陈胜，郭晓敏，刘晓宏，黄文进（.河海大学能源与电气学院，江苏南京00；.盐城供电公司，江苏盐城400）

基于模糊隶属度的电力系统抗差估计

陈妤1，陈胜1，郭晓敏2，刘晓宏2，黄文进2
（1.河海大学能源与电气学院，江苏南京211100；2.盐城供电公司，江苏盐城224002）

提出了一种电力系统模糊自适应抗差估计（fuzzy adaptive robust estimation，FARE）方法。计及了量测权重的不确定性，以连续的模糊隶属度评价测点的优劣，很好地解决了测点非优即劣的问题，以最小化测点劣质性的加权模糊隶属度之和为优化目标，采用原对偶内点法（Primal-Dual Interior Point Method，PDIPM）求解，并且实现了对量测粗差的自适应。多个IEEE标准算例以及波兰系统的仿真测试结果表明，该方法具有良好的抗差性能。

权重不确定性；模糊隶属度；抗差估计；原对偶内点法

作为能量管理系统（energy management system，EMS）的基石，电力系统状态估计根据遥测的生数据，估计出电力系统的实时运行状态[1-2]。传统的加权最小二乘[3-4]（weight least squares，WLS）的估计精度易受不良数据的影响[5]，一种实用的处理方法是在状态估计之前添加不良数据检测辨识程序[3]，最大正则化残差检测是最常用的不良数据检测辨识方法，但这种处理方法不足之处在于涉及了大量矩阵求逆计算，即便采用高效的稀疏技术，其计算复杂度也随着量测规模等比例增长。

相比而言，抗差估计器以一定的估计准则，在估计过程中实现了对不良数据的自适应，无需额外的不良数据检测辨识程序，因而引起了国内外大量学者的研究。抗差估计器包括加权最小绝对值[6-7]（weighted least absolute values，WLAV）、非二次准则[8]、指数目标型[9-10]、最大合格率[11]等。但现有抗差估计、不良数据监测辨识理论粗糙地将量测量分为2类：优质量测和劣质量测，这种对量测量非优即劣的区分显然是不够合理的[12]。

本文提出一种电力系统模糊自适应抗差估计（fuzzy adaptive robust estimation，FARE）方法，首先以连续的模糊隶属度函数评价测点的相对优劣性，避免了测点非优即劣的问题；其次考虑到随着设备的老化、运行环境的时刻变化，仪表的量测精度难以持续保持稳定，对量测仪表进行重新校核必须付出很大的经济代价，因而很难系统地重新校核量测仪表，也就是说，量测方差是随时间变化的，难以精确估计，即量测权重存在不确定性。本文基于测点模糊隶属度在线修正量测标准差，实现了对量测粗差的自适应，以最小化测点劣质性的加权模糊隶属度之和为优化目标，采用原对偶内点法[6，13]（primaldual interior point method，PDIPM）求解。多个IEEE标准算例以及波兰系统的仿真测试结果，验证了本文方法的有效性。

1　电力系统模糊自适应抗差估计

1.1测点优质性的模糊隶属度

电力系统状态估计量测方程为

式中：x为状态向量；设系统节点数为n，则x包含节点电压的幅值和相角，其维数为2n-1；z为m维量测向量；h（x）为量测函数向量；e为量测误差向量，且假设量测误差服从正态分布。

状态估计的残差方程为

式中：r为m维残差向量；x*为状态量x的估计值。

则对于第i个测点，若其估计残差ri很小，则可认为该测点为优质测点；反之，若其估计残差ri很大，则可认为该测点为劣质测点。由于各个测点的量测精度不同，定义σi为测点i的量测标准差，因而以测点的加权残差的σi/ri大小区分优劣测点更为合理。

定义事件y为测点的优劣，若集合Y包含了所有事件y，那么元素y与集合Y的关系可用一个特征函数——隶属度函数v（y）表示，对于经典的数据集合理论，有：

但实际测点的优劣只是相对的概念，即不存在绝对的优与劣，相比于经典的数据集合理论，模糊集合允许隶属度取[0，1]上的任何值，本文选取连续可微的钟形隶属度函数，对于第i个测点，其劣质性的模糊隶属度函数为

式中：a、b为大于0的模糊隶属度特征参数。

采用钟形模糊隶属度函数后，测点的相对优劣隶属度问题很好地被归一化到区间[0，1]上，很好地解决了测点非优即劣问题。

1.2基于测点优质性模糊隶属度的状态估计模型

以加权最小二乘（weighted least squares，WLS）为主的电力系统状态估计算法以最小加权残差平方和为优化目标，类似地，本文基于测点优质性的模糊隶属度，以最小化测点劣质性的加权模糊隶属度之和为优化目标，提出如式（5）所示的优化模型：

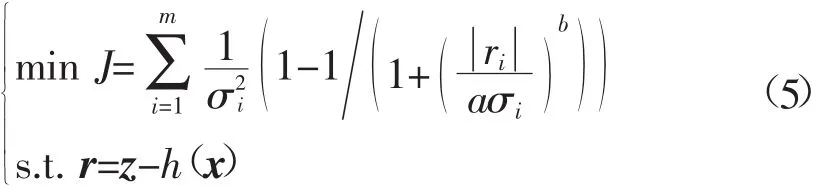
1.3量测权重的不确定性

目前，国内外绝大多数状态估计算法均是假设量测方差σ2已知，而在实际工程中，大规模电力系统中存在众多量测仪表，对量测仪表进行重新校核必须付出很大的经济代价，因而很难系统地重新校核量测仪表；此外，随着设备的老化、运行环境的时刻变化，仪表的量测精度难以持续保持稳定[14]。也就是说，量测方差是随时间变化的，难以精确估计，即量测权重存在不确定性。文献[15]中基于WLS以连续多个断面的量测残差离线估计量测权重，但在当网络拓扑改变以及固定时间窗口下，需在线更新权重，且需要专门的不良数据检测辨识程序事先剔除不良数据，大大增加了状态估计算法的计算时间。而国内实际系统的状态估计一般主观设置各量测的权重因子，调试及维护复杂，且主观设定的权重因子未必与实际量测方差吻合。

为此，本文基于测点模糊隶属度修正量测标准差，即对于求解式（5）过程中的第k+1次迭代，令：

量测标准差修正函数f（v）应遵循2个准则：

1）当测点模糊隶属度vi接近1时，此时该测点为优质测点，应保持近似不变。

2）当测点模糊隶属度vi接近0时，此时该测点为劣质测点，应增大σi，即出现量测粗差时，应降低该测点在迭代中的权重，减小其对状态估计结果的影响。

基于1）、2）准则，可选取修正函数f（v）=1－（1/v）1/b。

本文所述算法在考虑测点优质性模糊隶属度的基础上，实现了对量测粗差的自适应，故将该算法称为模糊自适应抗差估计（fuzzy adaptive robust estimation，FARE）。

2　基于原对偶内点法FARE模型求解

由于直接求解目标函数的不可微性，难以直接求解式（5），参照文献[3-4]中对的处理方法，引入m维非负松弛因子l、u，则式（5）可等价为

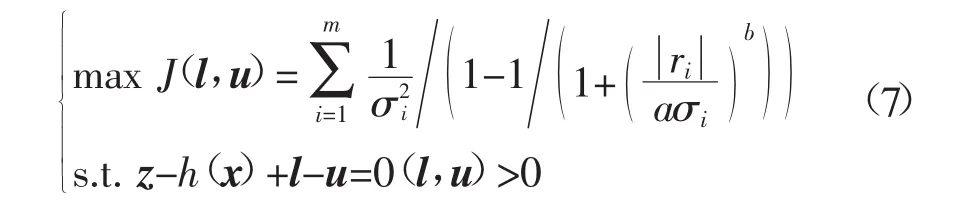
式（7）属于最优潮流问题，现代内点法[3-4]具有收敛性好，计算速度快，受初值影响小，适于求解大规模问题等优点，因而选用原-对偶内点法求解式（7）。

引入m维非负松弛因子l、u，则优化目标可等价为

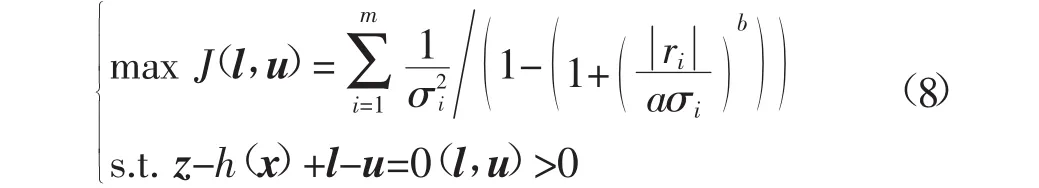
将式（8）中的等式约束设为障碍函数，可得拉格朗日函数：

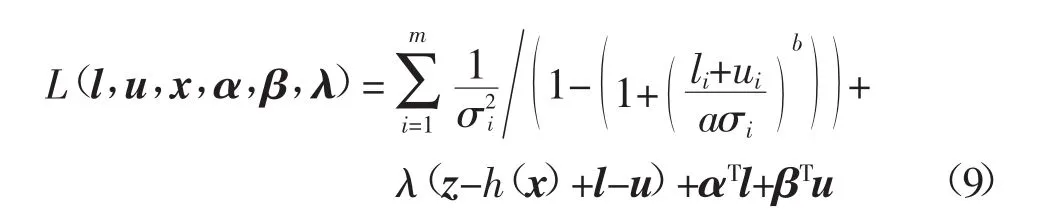
式中：λ、α、β为m维拉格朗日乘子，即对偶变量；l，u为原变量。

求解其KKT条件可得：

KKT条件为非线性方程组，可用牛顿-拉弗森法求解，将其线性化后得到修正方程组：

式（16）—式（21）可写成矩阵形式：

计算对偶间隙Gap=αTl+βTu及扰动因子μ=δGap/ 2m。此外，为了保证松弛因子恒为非负，依据式（23）—式（26）原、对偶变量的迭代步长（θr，θD）:

修正原、对偶变量：

修正量测标准差：σ（k+1）=σ（k）（1/v）1/b。

重复式（22）—式（26）修正过程，直至对偶间隙Gap达收敛精度或迭代次数超过设定的最大迭代次数。

3　算例分析

本文的测试算例包括IEEE14、30、57、118节点，波兰2383、2746节点（以WP-2383，WP-2746表示），量测数据由严格潮流结果添加随机量测误差得到，考虑量测标准差的不确定性，电压量测标准差服从[0.002，0.005]的均匀分布，功率量测标准差服从[0.004，0.010]的均匀分布。量测冗余度[2]介于3.5～ 4.5之间。并且随机添加10%的不良数据，不良数据在量测数据的基础上加减[5，20]倍的最大量测标准差。

为验证本文提出的FARE算法的优越性，将FARE与以往提出的状态估计算法，包括WLS、WLAV[6]、QL[3]进行抗差性能比较。WLS、WLAV、QC算法的电压量测权重取4，有功、无功量测权重取1。对于FARE算法的量测标准差初值σ（0），由于式（6）的修正是使σ在迭代中逐步增大，故σ（0）的选择应小于实际可能的量测标准差，本文电压量测σ（0）取0.001，有功、无功量测σ（0）取0.002；模糊隶属度参数取a= 2.5，b=3。

3.1不良数据辨识性能及残差污染测试

3.1.1残差污染及残差淹没

在单个不良数据的情况下，基于WLS的不良数据检测与辨识程序可能检测出不止一个可疑数据，即除了不良数据点的残差超过门槛值外，一些正常测点的残差也超过门槛值，即“残差污染”现象；而在多个不良数据下，残差污染将更为严重，甚至出现“残差淹没”现象，即不良数据点不能呈现任何残差特征。同时，当杠杆量测点的量测为不良数据时，更易出现残差污染及淹没现象，对状态估计的影响更大。

3.1.2杠杆量测的定义及辨识

对于WLS算法，其估计残差r与量测误差e关系为

式中：S为残差灵敏度矩阵；W为权重矩阵；H为量测雅克比矩阵。

如果对于第i个测点，其残差灵敏度矩阵对角元素Sii很小，则测点i的残差不能真实反映量测误差，即该测点是杠杆量测点。此外，杠杆量测的存在与量测的冗余度k軈相关，且当Sii<1－2时，可认为测点i是杠杆量测点。

在量测配置、网络拓扑相对固定的情况下，量测雅克比矩阵H受运行状态影响较小，因而杠杆点主要取决于系统本身的性质，可根据WLS算法离线辨识杠杆量测点。

3.1.3算例测试

假设由WLS离线辨识的杠杆量测点为集合N，非杠杆量测点为集合M，某个测点为不良数据记为事件l。为更好地测试杠杆量测点出现量测粗差下，各种状态估计算法的性能，不良数据测点按式（29）原则随机选取：

事件a：不良数据点为杠杆量测点；事件b：不良数据点为非杠杆量测点。则式（29）使得事件a发生的概率为事件b发生概率的3倍。

为比较各种算法的不良数据辨识以及抵御残差污染淹没的性能，在量测真值、量测标准差真值已知的情况下，定义：

以IEEE14、IEEE118为测试算例，依照式（29）的准则随机添加不良数据，4种状态估计算法下τ的百分比分布如图1、图2所示。

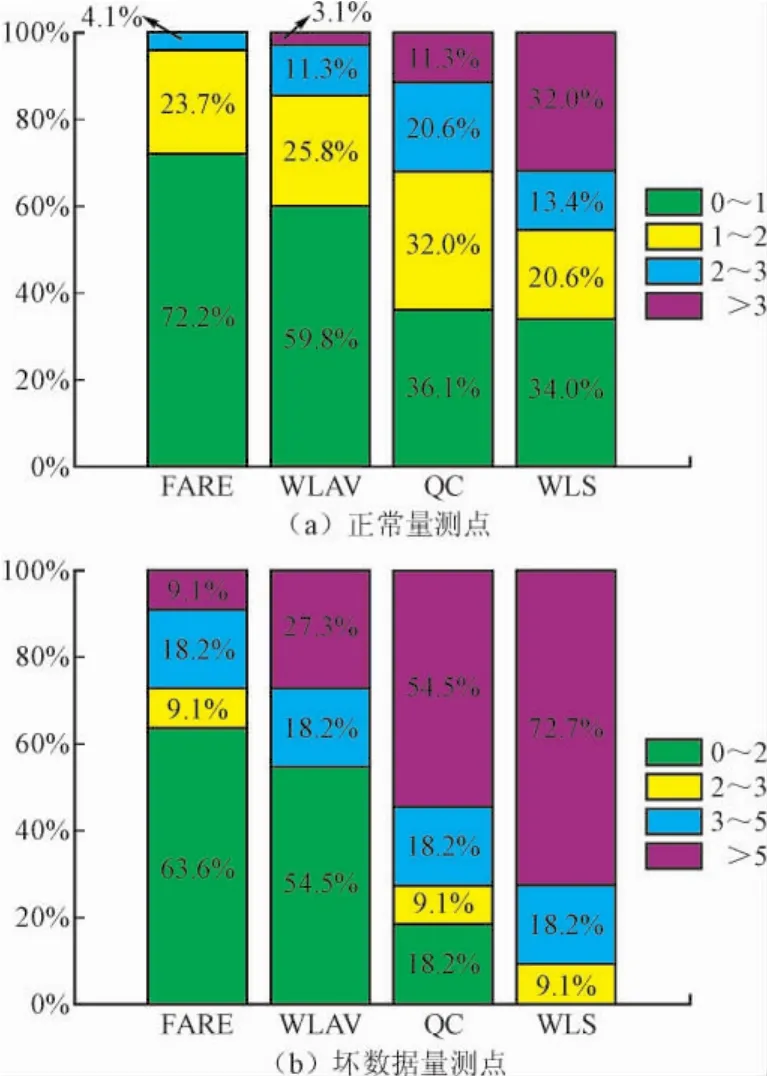
图1　IEEE14节点不同状态估计算法下τ百分比分布Fig.1　The percentage distribution of τ by different methods for IEEE14-node system

由图1与图2可知，WLS算法估计下的τ>3的百分比在20%以上，而量测不良数据比例仅为10%，这说明出现了很严重的残差污染淹没现象，因而基于WLS的QC算法也很难有效辨识不良数据及抵御残差污染淹没。相比于WLAV、QC、WLS算法，FARE算法估计下τ的分布主要集中于0～2之间，且τ>5的比例明显少于其余3种算法，因而FARE算法下的量测估计值更接近于量测真值，有着很好的不良数据辨识及抵御残差污染淹没性能。

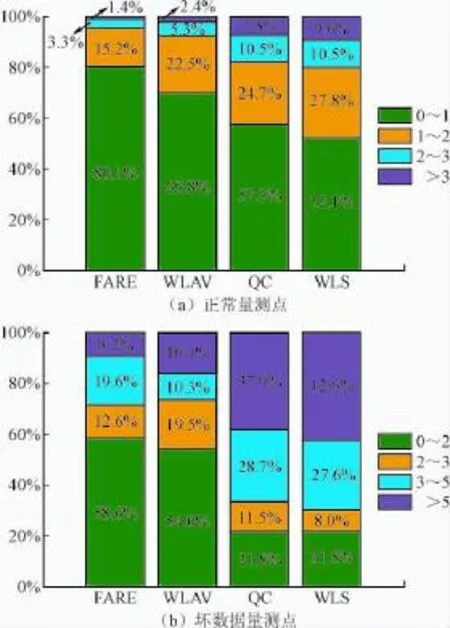
图2　IEEE118节点不同状态估计算法下τ百分比分布Fig.2　The percentage distribution of τ by different methods for IEEE118-node system

3.2抗差性能与收敛性能测试

采用以下3个指标来评价不同状态估计算法对状态量的估计性能。

1）电压幅值的均方误差：

式中：Vi为节点电压幅值的真值，V为节点电压幅值的估计值。

2）电压相角的均方误差：

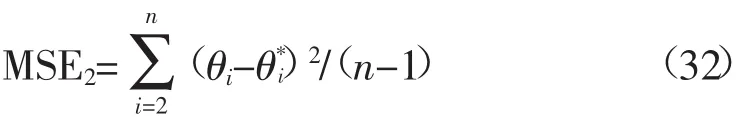
3）量测量估计准确度。实际运行中，除了对系统状态量的估计，用户更关心对量测量的估计效果，因此定义式（33）指标来评价不同状态估计算法对量测量的估计性能（实际系统以合格率评判量测量的估计性能）：

在6个测试算例均含10%不良数据的情况下，4种状态估计算法的评价指标如表1和表2所示。

在各测试系统含10%不良数据时，从表1、表2的测试结果可以看出：

1）状态量的估计性能方面，比较表1中MSE1和MSE2的大小，可知各算法对状态量的估计性能为FARE>WLAV>QC>WLS，且FARE明显优于其余3种算法。此外，FARE算法对电压相角的估计性能要好于对电压幅值的估计性能。

2）量测量的估计性能方面，比较表2中MSE3的大小，FARE对量测量的估计性能稍好于WLAV，QC次之，WLS最差。

3）收敛性能方面，WLS、QC以牛顿法求解，QC在WLS的基础上包含了不良数据检测辨识的功能；WLAV和FARE均以内点法求解。从表2中的迭代次数可看出，WLS收敛性能最优，其余3种算法收敛性能相近，且FARE的收敛性能要稍好于WLAV。

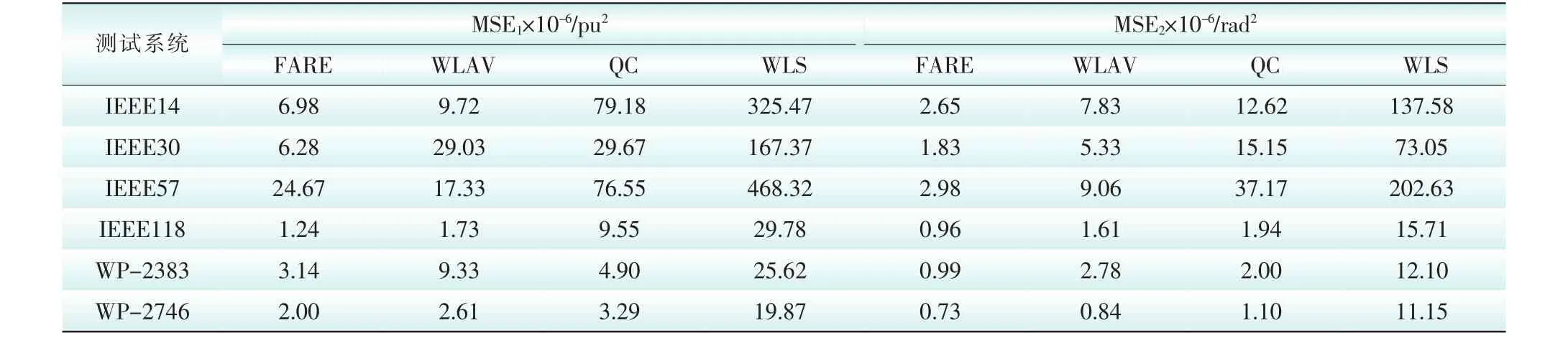
表1　含10%不良数据下不同估计算法的MSE1及MSE2指标性能Tab.1The performance of MSE1and MSE2by different algorithms with ten percentage of bad data

综合1）—3）的比较，WLS虽有最佳的收敛性能，但抗差性能薄弱；其余3种算法收敛性能相近，但FARE的抗差性能明显优于WLAV、QC，因而在本文选取的状态估计算法中，FARE是最优质的电力系统状态估计算法。

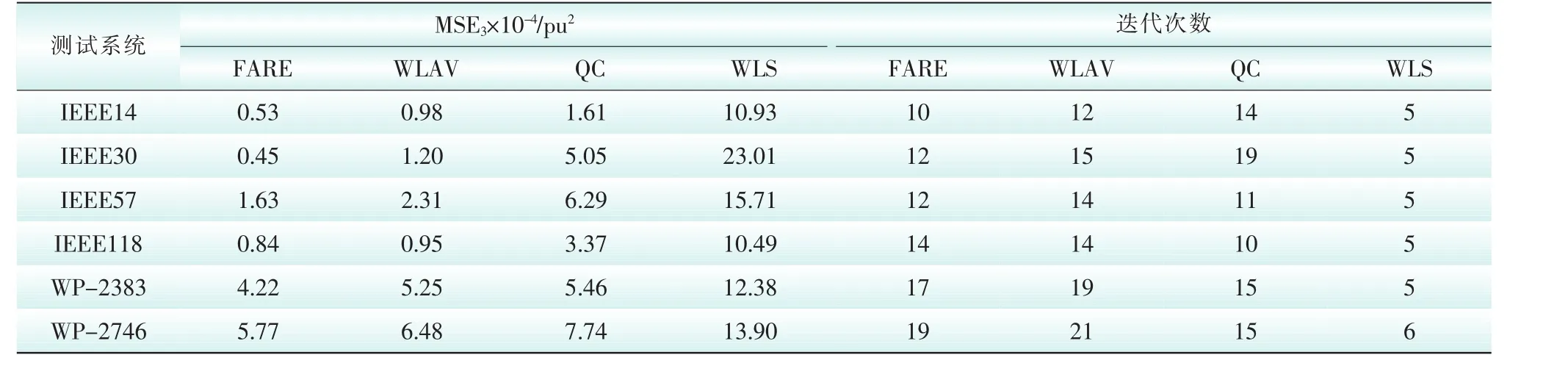
表2　含10%不良数据下不同估计算法的MSE3指标性能及迭代次数Tab.2The performance of MSE3and times of iteration by different algorithms with ten percentage of bad data

4　结论

本文提出的算法以模糊隶属度定量评价测点的相对优劣性，避免了测点非优即劣的问题，且基于测点的模糊隶属度自动更新量测权重，实现了对量测粗差的自适应，有着良好的抗差性能。本文所提方法的特点：

1）无需进行不良数据校验，无需主观设定权重，易于调试与维护。

2）在迭代的过程中依据模糊隶属度自动辨识不良数据，实现对量测粗差的自适应，其状态估计结果主要受优质量测影响。

3）如果在连续多个断面下，某个测点的量测权重均远小于其余测点，则该测点的量测仪表很可能损坏或数据传输通道出现故障，因而该方法易于查找出量测中的故障。

[1]田江，钱科军，梁锋．分布式状态估计技术在智能变电站的应用[J]．电网与清洁能源，2013，29（9）：27-31．TIAN Jiang，QIAN Kejun，LIANG Feng．Application of distributed state estimation in smart substations[J]．Power System and Clean Energy，2013，29（9）：27-31（in Chinese）．

[2]冯永青，刘映尚，吴文传，等．电力系统状态估计调试方法研究[J]．南方电网技术，2007，1（1）：46-51．FENG Yongqing，LIU Yingshang，WU Wenchuan，et al． Study on maintenance methods of power system state estimation[J]．Southern Power System Technology，2007，1（1）：46-51（in Chinese）．

[3]ABUR A，EXPOSITO A G．Power system state estimation：theory and implementation[M]．Florida:CRC Press，2004．

[4]李虹，李卫国．基于提高系统可观测性和状态估计精度的PMU配置[J]．华北电力大学学报，2011，38（1）：31-34．LI Hong，LI Weiguo．A new method of PMU placement for improving network observability and state estimation precosion[J]．Journal of North China Electric Power University，2011，38（1）：31-34（in Chinese）．

[5]孙国强，卫志农，周封伟．改进迭代自组织数据分析法的不良数据辨识[J]．中国电机工程学报，2006，26（11）：162-166．SUN Guoqiang，WEI Zhinong，ZHOU Fengwei．The applicationofISODATAtobaddatadetectionand identification based on genetic algorithms[J]．Proceedings of the CSSE，2006，26（11）：162-166（in Chinese）．

[6]WEI H，SASAKI H，KUBOKAWA J，et al．An interior point method for power system weighted nonlinear L1 norm static state estimation[J]．IEEE Trans on Power Systems，1998，13（2）：617-623．

[7]颜全椿，卫志农，孙国强，等．基于多预测-校正内点法的WLAV抗差状态估计[J]．电网技术，2013，37（8）：2194-2200．YAN Quanchun，WEI Zhinong，SUN Guoqiang，et al．A robust WLAV state estimation based on multiple predictorcorrector interior point method[J].Power System technology，2013，37（8）：2194-2200（in Chinese）．

[8]郭伟，单渊达．M估计方法及其在电力系统状态估计中的应用[J]．中国电机工程学报，2000，20（9）：26-31．GUO Wei，SHAN Yuanda．M-estimation and its application in power system state estimation[J]．Proceeding of the CSSE，2000，20（9）：26-31（in Chinese）．

[9]吴文传，郭烨，张伯明．指数型目标函数电力系统抗差状态估计[J]．中国电机工程学报，2011，31（4）：67-71．WU Wenchuan，GUO Ye，ZHANG Boming．A robust state estimation method with exponential objective function[J]．Proceedings of the CSSE，2011，31（4）：67-71（in Chinese）．

[10]郭烨，张伯明，吴文传．指数型目标函数电力系统抗差状态估计的解法与性能分析[J]．中国电机工程学报，2011，31（7）：89-95．GUO Ye，ZHANG Boming，WU Wenchuan．Solution and performance analysis to a robust state estimation method with exponential objective function[J]．Proceedings of the CSSE，2011，31（7）：89-95（in Chinese）．

[11]董树锋，何光宇，孙英云，等．以合格率最大为目标的电力系统状态估计新方法[J]．电力系统自动化，2009，33（16）：40-43．DONG Shufeng，HE Guangyu，SUN Yingyun，et al．A novel method for power system state estimation with maximum good measurement rate[J]．Automation of Electric Power Systems，2009，33（16）：40-43（in Chinese）．

[12]黄知超，谢霞，王斌．结合模糊综合评判与决策的电力系统状态估计[J]．电力系统保护与控制，2015，43（7）：65-69．HUANG Zhichao，XIE Xia，WANG Bin．Power system state estimation combined with fuzzy comprehensive evaluation and decision-making[J]．Power System Protection and Control，2015，43（7）：65-69（in Chinese）．

[13]周寅飞．基于内点法和离散粒子群算法的输电网参数辨识[J]．江苏电机工程，2014，33（1）：22-25．ZHOU Yinfei．A hybrid strategy based on interior point method and DPSO for electricity transmission network parameter estimation[J]．Jiangsu Electrical Engineering，2014，33（1）：22-25（in Chinese）．

[14]AL-OTHMAN A K，IRVING M R．Uncertainty modelling in power system state estimation[J].Generation，Transmission and Distribution，IEE Proceedings IET，2005，152（2）：233-239．

[15]ZHONG S，ABUR A．Auto tuning of measurement weights in WLS state estimation[J]．Power Systems，IEEE Transactions on，2004，19（4）：2006-2013．

（编辑董小兵）

Power System Robust Estimation Based on Fuzzy Membership

CHEN Yu1，CHEN Sheng1，GUO Xiaomin2，LIU Xiaohong2，HUANG Wenjin2
（1.College of Energy and Electrical Engineering，Hohai University，Nanjing 211100，Jiangsu，China；2.Yancheng Power Supply Company，Yancheng 224002，Jiangsu，China）

This paper proposes a Fuzzy Adaptive Robust Estimation（FARE）method.The method judges the quality of measurements based on the continuous fuzzy membership function considering the uncertainty of the measurements’weights to avoid the judgment that regards a measurement as either god or bad，and the optimal objective lies in the minimal sum of weighted fuzzy membership，which is solved by the Primal-Dual Interior Point Method（PDIPM，and the self-adaption to the gross errors is realized too.Simulated results on several IEEE standard systems and a polish system indicate that the method proposed in this paper has a robust performance against gross errors.

uncertainty of the measurements’weights；fuzzy membership；robust estimation；PDIPM

1674-3814（2015）07-0013-07中图分类号：TM711

A

国家自然科学基金资助项目（51277052）；国家电网公司科技项目“基于EMS的电网参数辨识及抗差状态估计研究”。

Project Supported by National Natural Science Foundation of China（51277052）；State Grid Corporation of China.

2015-03-17。

陈妤（1993—），女，本科，从事电力系统分析与控制方面的研究；

陈胜（1990—），男，硕士研究生，从事电力系统状态估计，优化潮流方面的研究。