彩色图像3D-DCT的熵编码方法研究

杨树媛，纪朝凤（新疆农业大学计算机与信息工程学院，乌鲁木齐830052）

彩色图像3D-DCT的熵编码方法研究

杨树媛，纪朝凤
（新疆农业大学计算机与信息工程学院，乌鲁木齐830052）

在彩色图像的三维离散余弦变换压缩体系中，交流系数游程编码后存在大量的长零游程，传统的JPEG基于（Run，Level）统计进行熵编码，压缩性能较差；通过对交流系数分布的研究，提出基于（Run Level，Level）的联合概率分布进行熵编码的改进方法，该方法码表简单，且可直接复用JPEG码表，有很大潜力应用于更高维的视频图像变换压缩领域。另外，根据非零系数的分布特点和编码效率分析，对密集区和疏散区域采用不同的编码方法。实验结果表明，在相同的PSNR下，较JEPG基线标准有11%的码流节省。

游程编码；熵编码；3D-DCT；图像压缩

0　引言

在彩色图像压缩领域，三维离散余弦变换（Three Dimensional Discrete Cosine Transform，3D-DCT）被认为是运动补偿的替代技术[1]，它利用RGB三帧的相关性（例如相同的纹理和相同的灰度、梯度），采用沿着帧方向的一维DCT的方法，来替代传统图像压缩标准中的色空间转换方法，以此消除色空间冗余。

JPEG对交流（Alternating Current，AC）系数编码的主要方法是：首先进行游程编码（Run Length Coding，RLC），然后将游程编码后的（Run，Level）数对进行霍夫曼熵编码（Entropy Coding，EC），即RL-EC方法，这里Run指的是连续零系数的长度，Level是非零系数幅值的数量级。关于RL-EC的改进算法，国内外已经进行了大量研究。针对连续的非零系数进行编码时，码流长度将会增加的问题，Tian提出了将非零AC系数的密集区和疏散区进行不同编码的思路[2]；基于当扫描位置不同时，系数分布的概率统计模型也是不同的现象，Lakhani提出了一种建立最优霍夫曼码表的方法[3]。跟传统的单上下文模型相比，姜提出了一种基于联合上下文模型的新方法[4]。

上文中的熵编码方法都是适用于基于2D-DCT算法编码器的，在3D-DCT中，存在一个新问题：游程编码后，出现更多的长零游程，并且游程长度大于15的非常普遍。针对这一问题，Fryza[5]将JEPG中的码表进行了扩展；对于游程长度大于15的零游程，邹[6]创建了一个额外的码表对其进行编码；但是，这两种方法的码表都太大了。很显然，改变编码模型是解决问题的关键。因此，在彩色图像的3D-DCT压缩系统中，本文提出了基于（Run Level，Level）的统计性进行熵编码的改进算法（IRL-EC）。该算法有许多优点：易于理解、码表开销适中、编码形式与RL-EC相似。另外，还根据扫描后非零系数分布的不均匀性，对不同区域的采用不同的编码方法。

1　彩色图像的3D-DCT压缩系统介绍

1.1彩色图像的三维建模和分块

一幅大小为M×N的彩色图像，它是由M×N大小的R、G、B三种颜色分量的灰度图像组成，则彩色图像的三维建模如图1所示，沿着x轴的方向为高度维，沿y轴方向为宽度维，沿z轴方向为帧维，则可以得到一个M×N×3的关于彩色图像像素值的三维模型。类似于JPEG，为了减少计算量，提高编解码速度，将M×N×3的三维模型统一分割为8×8×3的三维块依次进行3DDCT。

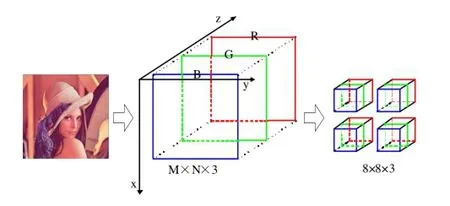
图1　彩色图像的三维建模和分块

1.23D-DCT

M×N×3大小的彩色图像三维块的3D-DCT定义为：

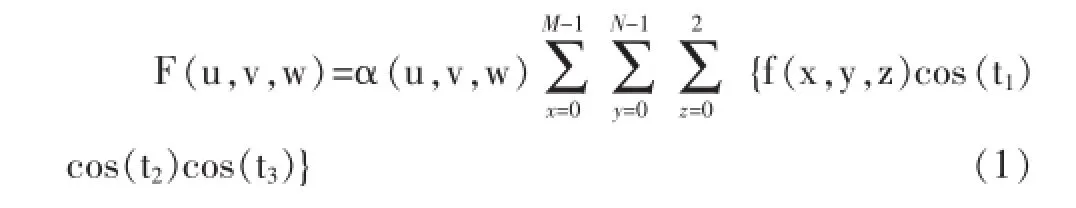
相应3D-IDCT为：

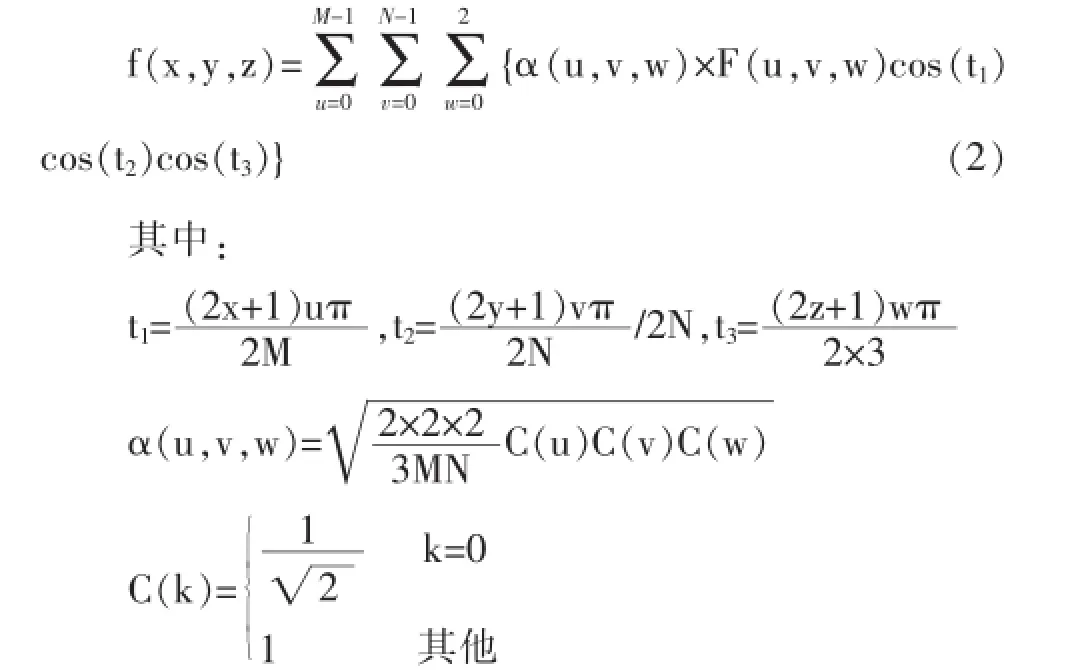
f（x，y，z）是变换前的第z个颜色分量帧内的灰度值，x=0，1，…，M-1，y=0，1，…，N-1，z=0，1，2；

F（u，v，w）为相应变换后的第w个DCT块内的系数，u=0，1，…，M-1，v=0，1，…，N-1，w=0，1，2。本文中M=N=8。

1.3量化和扫描

变换后主要能量都集中在低频区域，且人眼对于高频系数不敏感，定义三维量化矩阵如下：

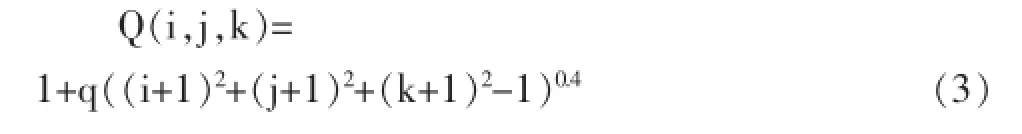
其中:

i∈[0，M-1]，j∈[0，N-1]，k∈[0，2]。q是量化因子，改变q的值就得到不同的量化级数。量化值在低频区域较小，随着（i，j，k）的增加而增大。扫描采用将JPEG中ZigZag扫描扩展到三维的方式。

2　熵编码

和JEPG一样，对DC系数的熵编码，首先进行无损预测编码，然后进行变长编码。另外，如果当前编码块左侧或上面块的直流系数为0，当前块的直流系数也很可能为0。由此，本文建立了两种码表，来基于上下文进行自适应编码。

DC编码格式：（Level）B（Amplitude）B

其中Level是DC系数的数量级，（Level）B是Level对应的二进制码字，（Amplitude）B是DC的幅值对应码字，假设Level是l，幅值为A，当A≥0时，码字是A对应二进制值的最后l位；当A＜0时，码字是|A|-1对应的二进制值的后l位。

2.1IRL-EC

RL-EC和IRL-EC的游程编码格式对比如下：

RL-EC：（Run，Level）

IRL-EC：（Run Level，Level）

其中，Run Level表示游程长度的数量级。

RL-EC和IRL-EC的熵编码格式如下：

RL-EC：（Run，Level）B（Amplitude）B

IRL-EC：（Run Level，Level）B（Run Length）B（Amplitude）B

其中，（Run，Level）B和（Run Level，Level）B分别是（Run，Level）和（Run Level，Level）对应的二进制码字，（Run Length）B是零游程长度对应的码字，假设Run Level是Rl，Run Length是A，当Rl=0或者Rl=1时，就不需要将游程长度进行熵编码，因为此时A=Rl；当Rl＞1时，码字是A-2Rl-1的二进制值的后Rl-1位。一个8× 8×3三维子块，Run Length的变化范围是[0，191]，相应Run Level的范围是[0，8]，而较JPEG码表，Run的变化范围为[0，15]，可见本文方法的码表小得多。

图2为在量化因子q分别为15、25、35、45时，经IRL-EC编码所得的（Run Level，Level）数对的概率统计柱状图。可以看出无论量化级是多少，较短的Run和较小数量级的Level出现的频率都更高，该统计特性和JPEG中RL-EC编码是类似的，因此本文直接复用JPEG根据（Run Level，Level）联合概率分布生成的码表。

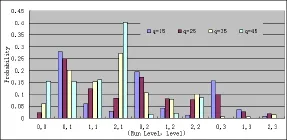
图2　 不同量化级时的（Run Level,Level）概率分布图

2.2码长分析

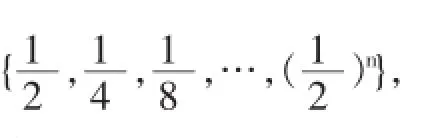
根据游程编码后（Run，Level）的统计规律，Run不变，随着Level的增大，（Run，Level）出现的概率逐渐降低。假定同一Run，不同Level的（Run，Level）的概率为{Pn}，则（Run Level，Level）具有相似的统计规律，因此概率也为{Pn}。如果Run是l，Run Level是k，采用RL-EC的平均码长（λl）和IRL-EC的的平均码长（λk）定义如下：

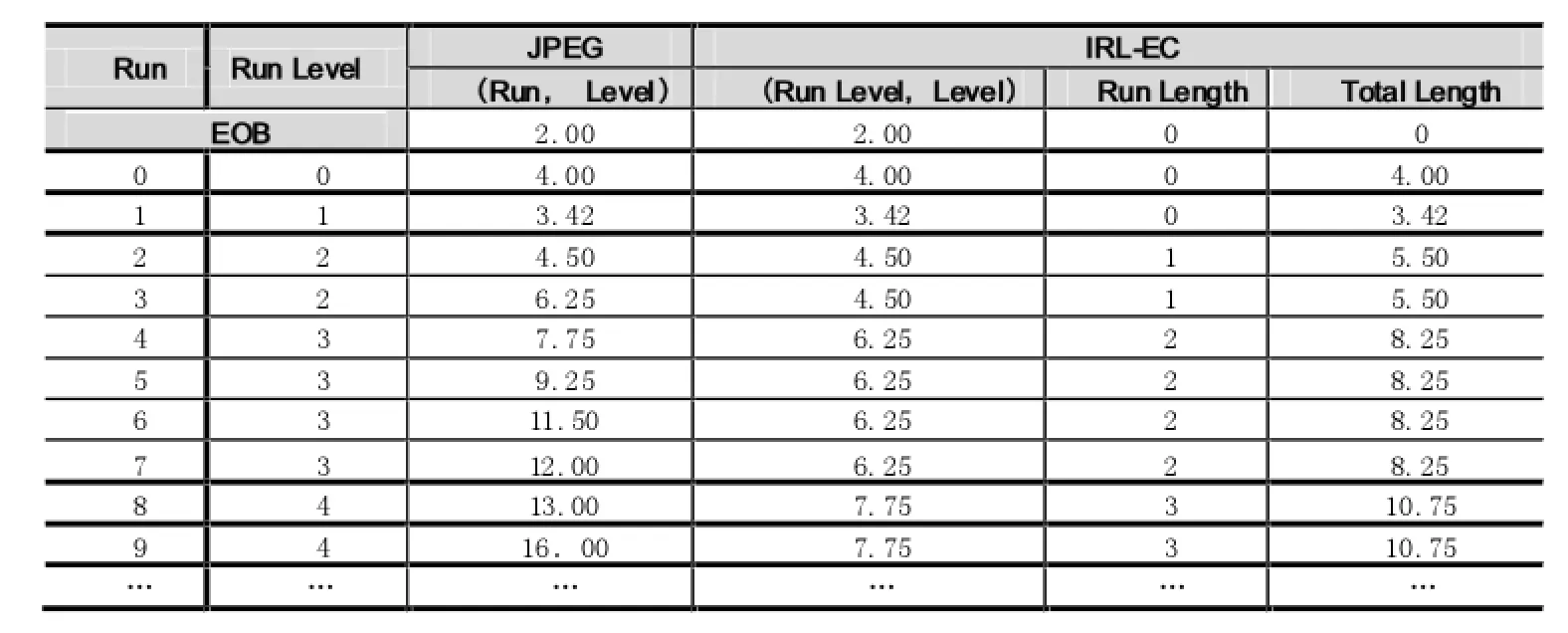
表1　平均码长对比

式中，Pn和λn分别是Level为n时，（l，n）数对出现的概率和对应的二进制码长。

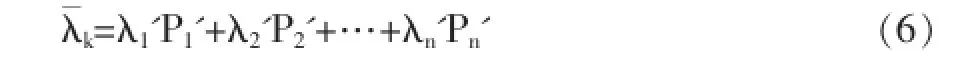
式中，Pn'和λn'分别是Level为n时，（k，n）数对出现的概率和对应的二进制码长。

JPEG算法与IRL-EC算法的平均码长对比结果如表1所示。可以看出，当游程长度大于4时，本文方法具有明显优势。由于编码后非零系数密集区的游程一般较短，疏散区的游程较长，因此可采用分段混合编码的方法，对于密集区采用JPEG中的RL-EC编码方法，疏散区采用本文提出的IRC-EC编码方法。

将疏散区和密集区分割的位置定义为断点，为了便于解码，EOB即（0，0）被视为断点的标识，其表示一种熵编码方法的结束和另一种熵编码方法的开始。由于最佳断点的选取不是本文的研究重点，本文断点位置选取为第10个AC系数处，即前10个系数采用RLEC编码，其余系数采用IRL-EC编码。

3　仿真结果和分析

实验选取标准图像数据库中的彩色图像，其大小为256×256，峰值信噪比（Peak Signal to Noise Ratio，PSNR）用来作为图像质量的客观评价标准，使用压缩比（Compression ratio，Cr）表示原图像和压缩后文件大小的比值。表2是本文方法和JPEG基线压缩系统[7]对比结果。其中比特率的节省率Sr计算定义如下：

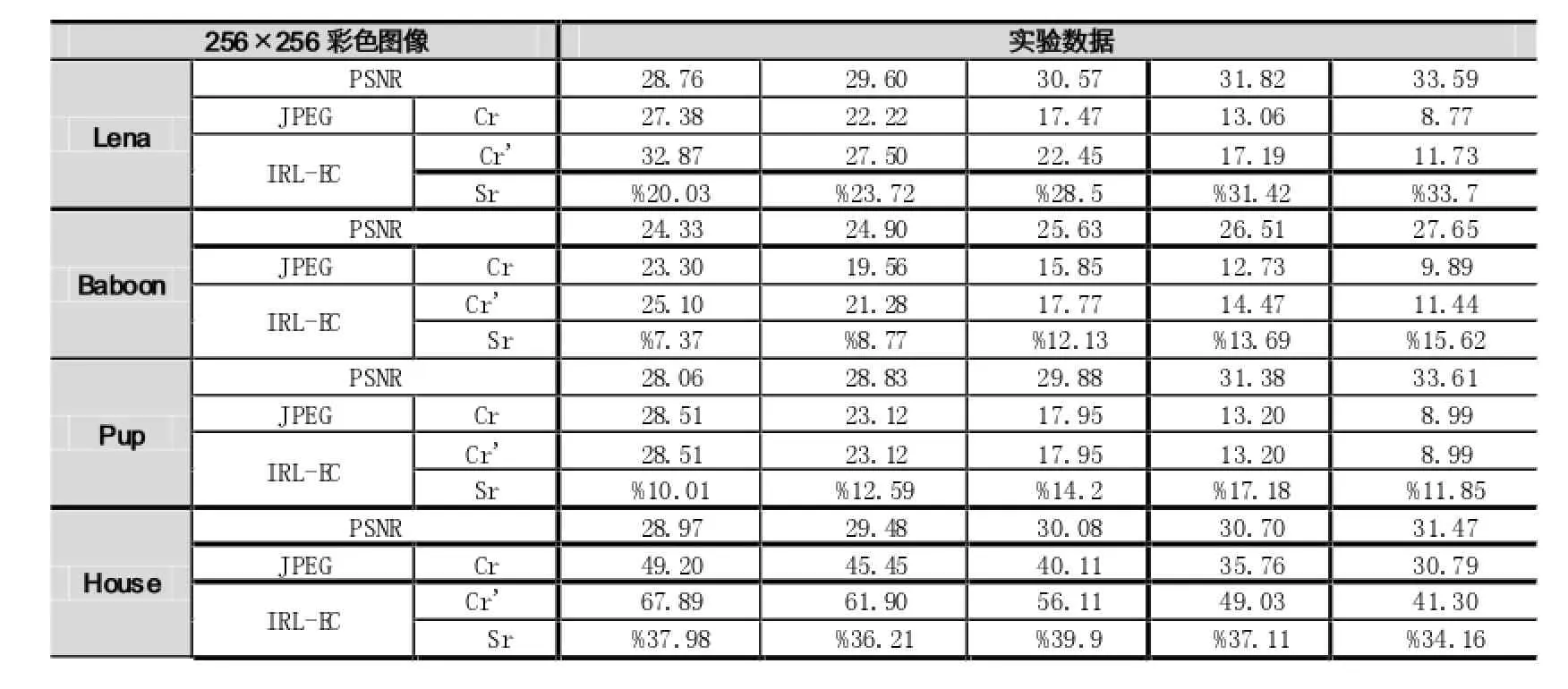
表2　本文方法和JPEG的图像压缩结果对比

其中Cr和Cr'分别表示采用JPEG和IRL-EC所得的压缩比。

从表2中可以看出，PSNR越大，文中方法的优点越明显，这是因为此时量化级较小，扫描系数中有较多的非零系数，长零游程出现的频率更高。

4　结语

本文是3D-DCT在图像压缩领域的进一步研究，基于扫描后系数中存在大量的长零游程这一特性，本文提出了一种改进的熵编码方法。当前，3D TV和3D手机等技术的快速发展应用，文中方法有广阔的发展空间应用于视频图像的多维变换压缩系统中。

[1]Natarajan T，Ahmed N.On Interframe Transform Coding.IEEE Transactions on Communication，1977，25（11）:1323-1329.

[2]Tian D，Chen W H，Chang P S，et al.Hybrid Variable Length Coding for Image and Video Compression.IEEE International Conference on Acoustics，Speech and Signal Processing，2007:I-1133-I-1136

[3]Lakhani G.Optimal Huffman Coding of DCT Blocks.IEEE Transactions on Circuits and Systems for Video Technology，2004，14（4）: 522～527

[4]姜丽丽，赵德斌.基于复合上下文的自适应熵编码器设计与实现[J].计算机应用于软件，2007，24（6）：98～100

[5]Fryza T.Properties of Entropy Coding for 3D DCT Video Compression Method.17th International Conference on Radioelektronika，2007:1～4

[6]邹鑫馨.基于3D-DCT的视频编码实现[D].电子科技大学硕士学位论文，2009

[7]黎洪松.数字图像压缩编码技术及其C语言程序范例[M].学苑出版社，1994

Run Length Coding;Entropy Coding;3D-DCT;Image Compression

Research on Entropy Coding of Three Dimensional DCT of Color Image

YANG Shu-yuan，JI Chao-feng
（College of Computer and Information Engineering，Xinjiang Agriculture University，Urumqi 830052）

In the compression system of three dimensional discrete cosine transform,there are lots of long zero run-lengths of alternating current coefficients,which are encoded by run length coding,traditional entropy coding method in JPEG based on the statistics of（Run,Level）is not suitable.By path of the study of distribution of AC,proposes the improved entropy coding algorithm based on jointly probability of（Run Level,Level）,the size of code table is moderate,code table in JPEG is multiplexed,and there is great potential in the higher dimensional transform compression field of video image in further.According to the non-uniformity of non-zero coefficient and the analysis of coding efficiency,the scattered and clustered areas of non-zero coefficients are coded with different methods.The experiment results show that,when the peak signal and noise ratio is the same,there is 11%code rate savings compared with the Baseline of JPEG standard.

1007-1423（2015）14-0062-05

10.3969/j.issn.1007-1423.2015.14.015

杨树媛（1984-），女，甘肃白银人，硕士研究生，讲师，研究方向为多媒体信息处理、软件开发

纪朝凤（1985-），女，新疆塔城人，硕士研究生，讲师，研究方向为电子信息技术

2015-03-19

2015-04-29