管道解耦计算正确性论证

陈星文

(上海核工程研究设计院工艺系统所，上海200233)

管道解耦计算正确性论证

陈星文

(上海核工程研究设计院工艺系统所，上海200233)

抗震分析中，核电厂、火电厂及各种石油化工厂房中的某些重要管道（如核电厂中的主管道）需做动力学时程分析，分析所需的位移时程来源于建筑厂房的抗震分析。从建筑厂房抗震模型得到的位移时程能否作为管道分析唯一的边界条件？是否应当在输入时程数据的同时，再考虑厂房的刚度对计算结果的影响？基于结构力学和有限元的基本理论，对上述计算方法的正确性做理论推导，并通过有限元实例进行静力工况和动力工况的计算验证。

时程分析；解耦；刚度

0　引言

核电厂、火电厂及各种石油化工厂房是由构筑物、管系、设备等组成的十分复杂的系统（图1，图2所示）[1~2]，在抗震分析过程中，不可能建立一个完整的，十分细致的厂房整体分析模型。因此，为了对电厂各个部件进行全面、可靠、细致和有效的抗震分析，必须将厂房各个部分分解成若干抗震子系统，很多子系统再分为更小的子系统，然后逐步依次进行抗震分析。

以管道抗震分析为例，核电厂、火电厂及各种石油化工厂房中，都存在着大量的管道来传递水、石油等介质，这些管道通过管道支撑伸根在建筑厂房中。抗震计算分析中，不可能将所有的管道与建筑厂房完全耦合计算，而需要通过解耦的方式来逐步完成计算。通常情况下，一般的管道抗震分析都采用响应谱的计算方法，但对于一些特殊的重要的管道（如核电站的主管道）或者需要精确分析的管道，需要采用时程分析方法。管道时程分析方法的设计输入为从厂房抗震分析中得到各管道支撑点的位移时程。

以图3所示的管道分析模型为例，该管道在抗震分析时，采用时程分析方法[3]，其设计输入时程数据为从厂房模型抗震分析中得到的各支撑点的位移时程。将该位移时程施加给图3所示的管道分析模型，即可完成管道的抗震分析。

图1　某核电厂整体示意图

图2　建筑厂房中管道图

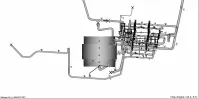
图3　管道计算模型示意图

根据管道的解耦计算过程，从主模型（厂房模型）中得到的解耦点的位移时程数据或载荷时程数据是子模型分析唯一的边界输入条件。这唯一的边界输入条件是否能够完全反应主模型中的相关因素，需要进行论证。因此，专家研究讨论时，就提出了以下的问题：

（1）从厂房模型得到的管道支撑处的位移时程，能否作为管道分析唯一的边界条件？是否应当在输入时程数据的同时，再考虑厂房的刚度对管道分析的影响？

（2）从厂房分析中得到的管道支撑点载荷，能否作为管道分析的唯一边界条件？支撑点载荷与管道的受力状态是否存在一一对应的关系，对于不同的管道变形状态，是否存在有同样的支撑载荷的情况发生？

1　解耦合理性的计算实例论证

为验证本文第一节所提出的两个问题，本节建立了两个简单的有限元模型，分别如图4和图5所示。其中，图4为主模型示意图，图5为将主模型从节点1和节点14解耦，所得到的子模型示意图。通过这两个相对简单的有限元模型的计算结果对比，可以作为主模型和子模型解耦计算准确性的一个辅证。

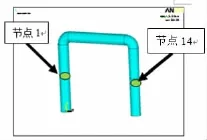
图4　主模型示意图

图5　子模型示意图

1.1静力计算工况

首先进行静力工况下的计算验证。图6为静力计算的主模型示意图。该模型由管道单元组成，管道单元为150×6的圆管。模型中施加任意的载荷，本例中施加的载荷为：22节点施加三个方向各0.01mm的线位移，10节点加100N向上的载荷。18节点完全约束，位移为0。通过求解，可以得到节点1和节点14的位移值和节点反力。

将图6所示的主模型从节点1和节点14断开，即得到图7所示的子模型示意图。子模型根据解耦点的加载形式，分为两种情况。一是给节点1和节点14施加从主模型中得到的位移值，再在10节点施加相同的100N向上的载荷，如图8所示。另外一种情况是，给节点1和节点14施加从主模型中得到的载荷值，10节点施加相同的100N向上的载荷。其模型如图8所示。

图6　主模型示意图

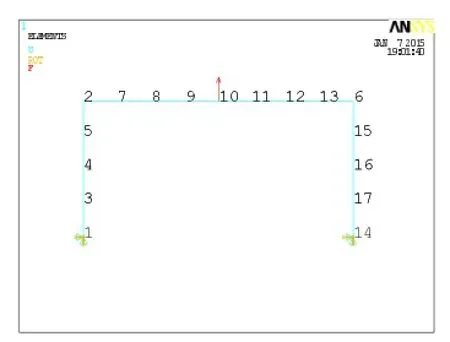
图7　子模型示意图（约束点边界条件为位移）

图8子模型示意图（约束点边界条件为节点载荷）

图8列出了上述三个模型中1~6号单元起始点所有6个方向的载荷，通过对比可以发现，三个模型计算的结果完全相同。其他单元的计算结果页完全相同，这里不再一一列出。

1.2动力计算工况

针对1.1节相同的模型，在主模型（图6）22节点处施加一位移时程，以模拟地震激励载荷，18节点仍为完全约束，位移为0，在节点10附加一100kg的质量点，以模拟结构的动力效应。节点22的输入位移时程如图10所示。通过主模型，求解到节点1和14的位移时程及力时程，将其施加在图7和图8所示的子模型中。

图9　主模型与子模型计算结果对比

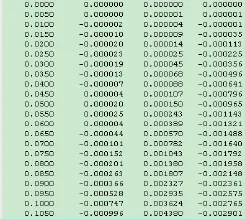
图10节点22位移时程

图11列出了主模型和子模型的动力计算结果。通过对比可以发现，主模型11节点和子模型中的11节点的位移响应完全相同。

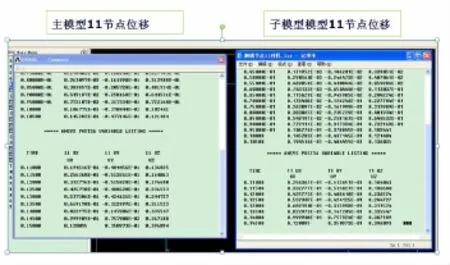
图11　主模型与子模型动力计算结果对比

2　解耦合理性的理论论证

结构的动力学计算方程如公式（1）所示[4]:

式中：K为结构的刚度矩阵，Δ为结构的位移矩阵，C为结构的阻尼矩阵，M为结构的质量矩阵，F为结构所受到的外载矩阵。

首先对结构的刚度矩阵进行相关的计算。设主模型共有n个自由度，则主模型的刚度矩阵如式（2）所示：

式中，刚度系数Kij为J方向自由度的单位位移在i方向自由度所产生的载荷。刚度系数Kl1至Klk为将要解耦的节点的自由度。

解耦点施加位移的子模型的刚度矩阵如公式（3）所示[5]，由于从主模型中删除掉了一些单元和节点，因此，假设其共有n-m个自由度。

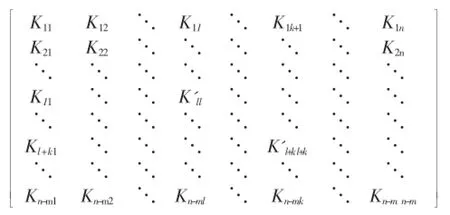
上式中的刚度系数与主模型中的刚度系数唯一的不同的是Kll'至K'l+kl+k。其代表的是解耦点的刚度系数。

Δl至Δ1+k为解耦点的节点位移，在Δl至Δ1+k相等的前提下，需论证公式（2）和公式（3）能够求得相同的解。

对公式（1）进行相应的推导计算，整体刚度矩阵中删掉不包含在子模型的自由度，得到公式（4）的刚度矩阵方程。

其他的系数与公式（2）完全相同。

Klr至Kl+ks为与解耦自由度相连，但不在子模型中的自由度在解耦点的刚度系数。

删掉公式（4）中的L至K行，再将刚度矩阵中的L至K列移到公式的右边，可得公式（5）的刚度方程。

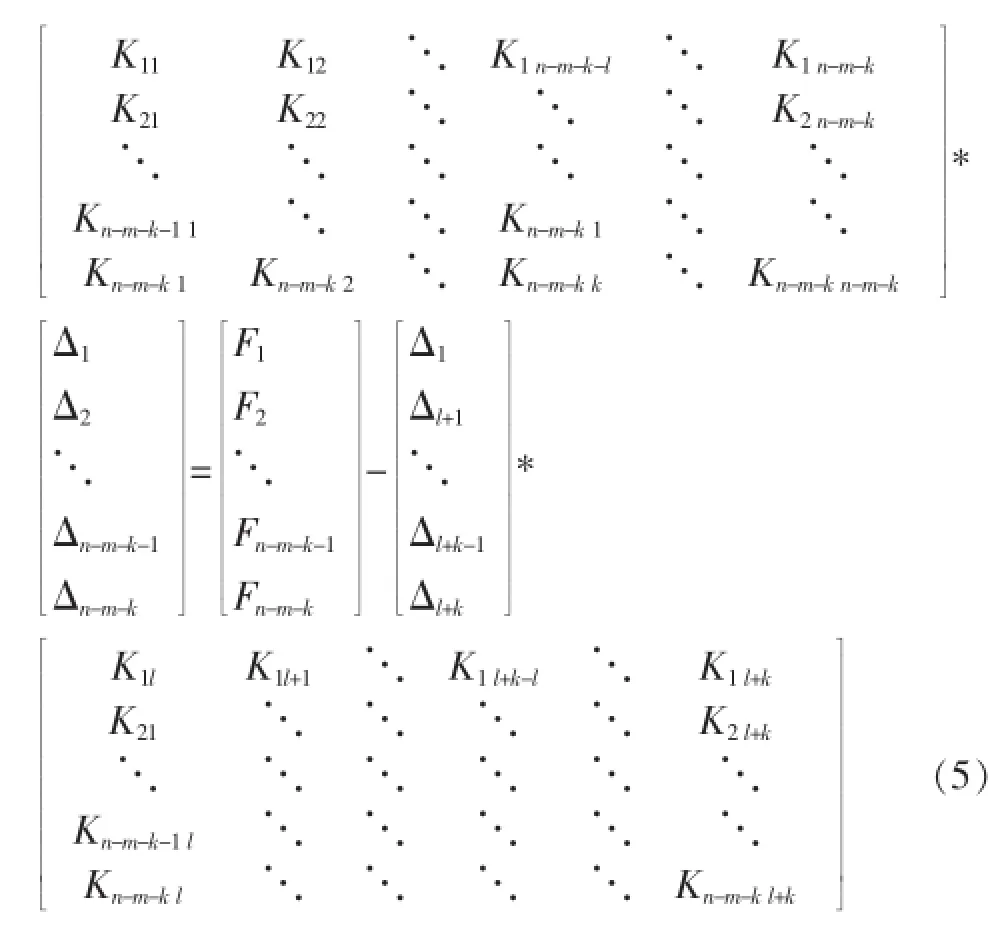
对子模型的刚度矩阵采用同样的计算方案，即删掉公式（3）中的L至K行，再将刚度矩阵中的L至K列移到公式的右边，同样可得公式（5）的刚度方程。

对于公式（5）中各个矩阵的意义[6]，阐述如下：

①方程左边的第1部分为子模型，除解耦点外的所有自由度的刚度矩阵，此部分矩阵，对于子模型与主模型是相同的。

②方程左边的第2部分为子模型需求解的节点自由度位移。

③方程右边的第一部分为子模型中，除解耦点外各个自由度接点上所承受的外载荷，此部分矩阵子模型与主模型相同。

④方程右边的第2部分为解耦点自由度的位移，即解耦点处施加的边界条件，此部分内容从主模型中提取，施加在子模型上，所以子模型与主模型中此部分内容相同。

⑤方程右边的第3部分为解耦点自由度对子模型中其他自由度的刚度系数，由于在解耦点赋予了同样的边界条件，所以此部分矩阵也不变。

因此，对于公式（5）中的各矩阵，子模型和主模型中的元素完全相同，主模型和子模型也必然求得相同的结果。

解耦点施加节点支反力的子模型的刚度矩阵如公式（6）所示：

小k为与解耦点相连接的不属于子模型中的单元刚度矩阵中的系数。

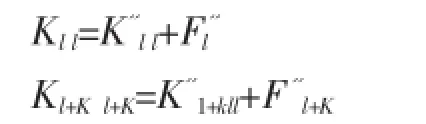
将公式（6）中的Fl''和F''l+K移至公式的左边，即可得到与公式（4）完全相同的方程。从而，可以得到结论，主模型与子模型所求解的结果完全相同。

另外，在动力学计算过程中，需考虑惯性对结构的影响，即需要考虑质量矩阵对方程的影响。而质量矩阵无论采用协调质量矩阵还是集中质量矩阵，在子模型输入边界条件一致的情况下，均能够与主模型求得完全一致的解。其推导过程与刚度矩阵相似，这里不再详述。

3　核电厂中某系统管道解耦计算结果对比

图12（a）是核电厂汇总某系统耦合钢结构模块和管道的主模型示意图，图12（b）为解耦后的管道子模型计算模型，其边界条件为从图12（a）模型中得到的回路支撑点位移时程。通过对两个模型所求得计算结果的对比，可以验证上述理论的准确性。表1列出了两个模型计算得到的相同支撑的最大载荷，通过载荷的对比可以发现，两者计算结果基本一致，误差较小。

表1　两种模型计算结果对比

图12　某系统耦合钢结构模块和管道的模型示意图

4　结语

本文针对管道计算的解耦计算问题，做了理论论证和有限元算例，得到了如下结论：

（1）主模型解耦点的位移可以作为子模型分析唯一的边界条件，不论是静力计算还是动力计算。子模型分析时，只需施加解耦点的位移，不需要再考虑其他的因素（前提是子模型中的单元与主模型施加同样的载荷）。

（2）主模型解耦点的载荷也可以作为子模型分析唯一的边界条件。子模型分析时，只需施加主模型中解耦点的载荷，不需要再考虑其他的因素（前提是子模型中的单元与主模型施加同样的载荷）。

本文所得到的结论适用于所有设备和管道的计算分析。

[1]林诚格.非能动安全先进核电厂AP1000[M].北京:原子能出版社,2008：5~82

[2]希年臧,申世飞.核电厂系统及设备[M].清华大学出版社.2003：280~290

[3]ASME锅炉与压力容器委员会核动力分委员会.ASME III-核设施部件建造规则[M].上海科技文化出版社，2004:NB-3600

[4]朱伯芳.有限单元法原理与应用[M].2版.北京:水利水电出版社，1998:33~95

[5]ANSYS Company.ANSYS 12.1 HELP[Z].USA:ANSYS Company,2009

[6]龙驭球，包世华，匡文琦等.结构力学教程[M].北京:高等教育出版社，1999：215~435

Correctness Proof of Pipeline Decoupling Calculation

CHEN Xing-wen

（Design of Institute，Shanghai Nuclear Engineering Research,Shanghai 200233）

In the process of seismic analysis,time history analysis is needed for some important piping systems in the nuclear power and thermal power plant.The time histories are from the seismic analysis of civil structure,and are the only inputs for the piping seismic analysis. Puts forward a question that whether should consider some other factors from the structure besides the displacement time histories,for example,the stiffness of the concrete.Through the research,illustrates that the displacement or force time history from the structure or main model can be the only inputs for the piping or sub_model analysis.

Time History Analysis;Decouple;Stiffness

1007-1423（2015）11-0032-06

10.3969/j.issn.1007-1423.2015.11.006

陈星文（1983-），男，山东青岛人，硕士研究生，工程师，研究方向为固体力学

2015-03-03

2015-03-11