运算律应该怎么教学
俞正强

不管是学生还是教师,都觉得运用乘法分配律很难,差错很多,因此,有许多学生很怕简便运算。这很令教师困惑:原本可以减轻计算负担的运算定律为何却成为学生的负担?下面我们以“乘法分配律”为例,讨论运算律应该怎么教学。
一、理解:算律是算法的“窍门”
计算教学的目标可以概括为四个字:又对又快。当将算律与算法放在一起时,相对而言,算法解决的是“对”的问题,而算律解决的是“快”的问题。算律是对算法的熟能生“窍”。因此,算律源于算法的运用。所以,算律的教学应该从算法的运用开始。为此,“乘法分配律”的教学应该有这样的流程。
流程一:练习,看谁算得又快又对。(独立完成)
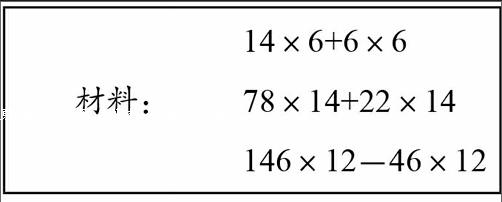
14×6+6×6
78×14+22×14
146×12– 46×12
……
设计意图:这些题目,学生在计算时会有以下两种方法。
方法1:按照“先乘除后加减”的算法进行计算
14×6+6×6
=84+36
=120
方法2:按照“几个几加几个几一共几个几”的意义理解进行计算
14×6+6×6
=20×6
=120
就当下的学生而言,对混合运算的算法,教师是教过的。但运用乘法意义来做这题目,则是学生自己的“调皮”,或者说是“窍门”。
流程二:讨论,怎样算得又对又快?
问题:我们能改变运算顺序吗?
结论:14个6加6个6一共是20个6。
设计意图:学生对乘法分配律的理解,在小学二年级算两位数乘一位数的时候,就已经蕴含其中了。
12×3→10×3+2×3=36
当时的理解是10个3加2个3一共是12个3。因此,学生理解14个6加6个6是20个6是很自然的事。也就是说,学生将这一类题目的运算顺序加以改变,十分自然。
流程三:讨论,我们改变运算顺序跟这些题目有关吗?是不是所有题目都可以改变运算顺序呢?
材料: 14×6+6×6
78×14+22×14
146×12-46×12
结论:运算特征: 乘 加(减) 乘 a×b±c×b
数字特征:有一个相同数 b
两个凑整数 a±c为一整数
设计意图:教师提供的这组练习题有两个特征:运算特征与数字特征。当满足这两个特征时,可以先加减后乘,这样就把运算律的前提条件给明确了。
流程四:判断这样算法,是又对又快吗?
① (25+14)×4 ② (15+45)×3
=25×4+14×4 =15×3+45×3
=100+56 =45+135
=156 =180
问题1:先算括号里面再算括号外面,这两道题目都没有先算括号里面,可以吗?
问题2:改变运算顺序的目的是什么?哪道题目的算法满足这个目的?
设计意图:几个几加几个几等于共有几个几,反之,共有几个几可以分为几个几加几个几。改变运算顺序的目的是为了又对又快,于是得出我们认可并推荐的“窍门”,将其命名为乘法分配律。
(a±b)c=ac±bc
流程五:练习(略)
二、讨论:算律是“规律”的运用
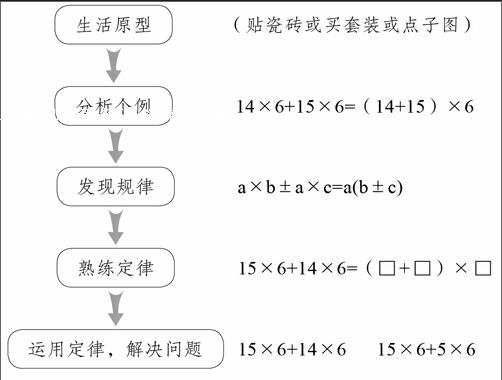
目前,教材基本上把算律归为“规律”,其基本流程如下。
与该流程相类似的在小学数学教学中通常限于“数学好玩”或“数学广角”等材料中,比如“打电话”。
我们可以比较打电话与乘法分配律两个教学内容,打电话需要分析个例发现规律,以解决比较繁杂的问题,这是正确的。但乘法分配律这个算律如果称之为规律,可以用意义来理解,不需要发现。把乘法分配律作为问题解决来教学,是在把简单问题复杂化。
三、推而广之:加法交换律应该怎么教学
一次,有位同事问:加法交换律的生活原型是什么?想了许久,也想不出加法交换律的原型。在去听课的过程中,发现有的教师会请两位学生到讲台上来,问其他学生:这是谁和谁?
然后将两位学生交换位置,问:这又是谁和谁?
学生回答:是谁和谁。
教师问:有没有变化?
学生回答:没有变。
教师又说:这是不是说明位置变了,大小没变啊?
学生回答:是的。
听了这个原型,心里有一种说不出的味道,书上是这样设计的:
一问:2+8=10
二问:8+2=10
三问:同学们,有什么发现吗?
问题是,2+8=8+2,这需要发现吗?难道不发现就不能知道2+8=8+2了吗?
那么,正确的呢?自然应从算法入手。
流程一:练习,看谁算得又对又快?
8+6+2
7+9+3
11+5+9
流程二:交流,谁算得又对又快?
从左到右依次计算→先凑整再相加。
流程三:讨论,这样改变运算顺序的理由是什么?
都是合并(加法意义)。
流程四:结论,连加算式中,如果能凑整,可以改变顺序,交换位置,即两个加数交换位置,和不变。
四、比较:差别在哪里
我们来比较两种教学流程所呈现的教学意义上的差别,如表1所示。
表1 两种教学流程呈现的教学意义上的差别
两种主张:对于知识而言,学生最终要记住ab±ac=a(b±c),并运用它以达到简便运算的目的,差别不大。但对知识的获得过程,两种主张的差别是巨大的。
本文主张要使学生深刻地认识到,算律脱胎于对算法的灵活运用,而灵活运用的依据是对运算意义的理解。教材主张的特征是割裂了算律与算法之间的密切联系,使之成为一个独立于算法的规律,把一个自然而然的“窍门”变成隆重的问题解决。
以上思考,仅供大家参考。
(责任编辑:孙建辉)

