基于子空间方法的风机齿轮箱故障预测算法

赵洪山，郭 伟，邵 玲，张兴科

（1.华北电力大学 电气与电子工程学院，河北 保定 071003；2.泰州供电公司，江苏 泰州 225300）

0 引言

风力发电是当前发展最为迅速的一种绿色能源，据中国风能协会的数据统计，2012年底我国风电并网总装机容量60.83 GW，跃居世界第一；发电量为100.4 TW·h，已经超过核电的98.2 TW·h，成为继煤电和水电之后的第三大主力电源。风电场一般坐落在广阔的偏远地区，受到恶劣的自然环境因素影响，再加上风机自身制造工艺和技术发展的不完善，这些因素都会增加风电机组发生故障的风险，且维修时往往很困难，造成风电场后期的运行维修费用居高不下。据统计，对于一台设计寿命为20 a的750 kW风机，它的运行和维修费用将占整个发电成本的 25%～30%，占其投资费用的 75%～90%[1]。

作为风机传动系统的关键部件，齿轮箱的任务是将风轮在风力作用下所产生的动力传递给发电机。虽然风机齿轮箱的制造工艺已较为成熟，故障率不高，然而一旦故障其修复过程很复杂，是造成风电机组停机时间最长的故障之一[2-3]。齿轮箱的故障一般是由轮齿损坏和轴承磨损造成的，在其故障发生之前，会有一段渐变的发展过程，在这个过程中会出现一些故障征兆信号。如果能提前识别出这些故障征兆，尽早采取措施，就可以避免演变为严重故障。

振动分析是一种有效的状态检测方法，尤其对于旋转机械设备[4]。如广泛应用于齿轮箱、轴承等风机部件振动故障检测的频谱分析[5]、小波变换[6]和Hilbert-Huang 变换[7-8]等时频分析技术，其中 Hilbert-Huang变换在处理旋转机械振动信号上要比前2种方法更为有效，但其缺点是耗时长[9]。另外，还有一些基于模型的故障诊断算法，如隐Markov模型[10-11]、支持向量机[12]和神经网络算法[13]等，它们一般都需要从振动信号中提取特征，并对数学模型进行训练，以实现对振动趋势的预测和故障识别。在过去的二十多年里，子空间识别方法应用于振动信号故障分析的发展也很快[14-15]，特别是对建筑物[16]和旋转设备[17]等都有较多的应用，但目前用于风电机组振动信号故障预测的研究还较少。该方法的特点是，直接在时域里分析数据建立模型，并识别相应的参数，不仅具有良好的数值稳定性和简易性，而且状态空间方程的形式非常适合于预测、滤波、估计和控制[18]。

1 问题的描述

子空间方法是一种利用已知数据建立多变量的线性状态空间模型的黑盒子识别方法，非常适合于振动信号的建模分析。随机子空间的线性状态空间模型描述如下：

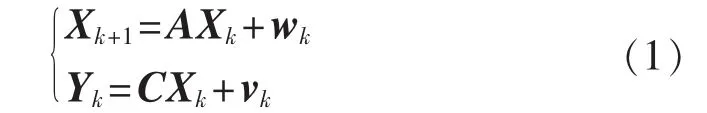
其中，Xk∈Rn和Yk∈Rl分别为在离散时刻k的状态量和系统的输出量；wk∈Rn和vk∈Rl分别为系统噪声和测量噪声，一般为不可观的向量；A∈Rn×n为系统矩阵，描述系统的动态行为；C∈Rl×n为系统输出矩阵。

本文利用子空间方法进行基于振动信号的风电机组齿轮箱故障预测。其基本思路为：首先，建立形如式（1）所示的齿轮箱随机状态空间模型；然后，利用正常运行振动监测数据估计线性模型的参数矩阵A和C，并计算出系统稳态运行时矩阵A的特征值，将其作为齿轮箱线性动态系统的参考特征值。当齿轮箱稳态运行时，由实时振动数据计算出的特征参数，与系统矩阵A的参考特征值误差很小；而当齿轮箱处于异常状态时，求得的系统矩阵A的特征值会偏离参考特征值，这样就可以实现对齿轮箱异常状态的识别。当特征值较多时，为避免对每个特征值都进行比较，定义了均方根误差这个总体评价指标，通过该指标可以从数值上直观识别出齿轮箱的故障状态。

2 随机子空间识别算法

2.1 正交投影

定义由量测量组成的分块Hankel矩阵Y：

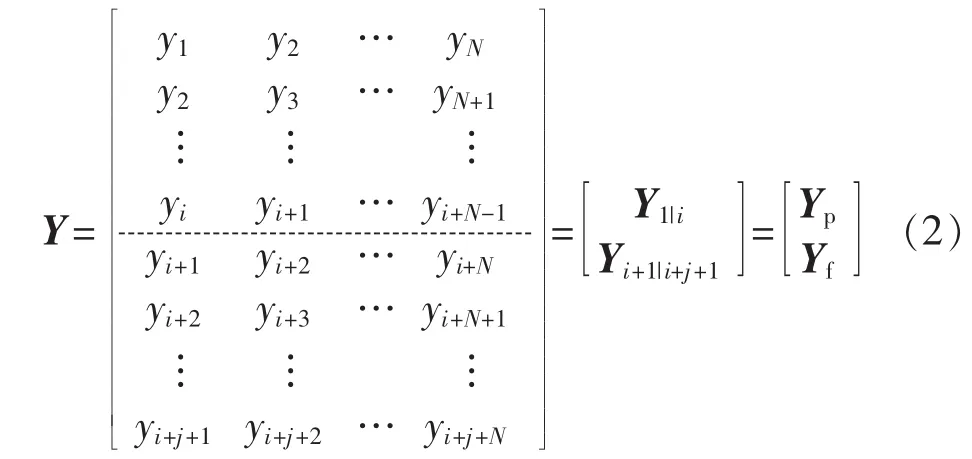
其中，｛yk｝k=1，…，i+j+N为系统的 i+j+N 个测量输出；Yp和Yf均为分块Hankel矩阵，其下标分别表示历史测量值和未来测量值；i和j+1分别为历史测量和未来测量形成分块矩阵的行数，一般不小于系统模型最大阶数 n，min｛i，j+1｝≥n；矩阵 Yp的维数为 i×N，矩阵Yf的维数为（j+1）×N，N≫max｛i，j+1｝。

对Y进行重新分块，如式（3）所示。

其中，Y+p为Yf的第1行移到了Yp的末行之后的矩阵；Y-f为Yf去掉了第1行后的矩阵。

将Yf正交投影到Yp的空间上，则正交投影Pm可以定义为：

其中，表示求Moore-Penrose逆。

同样对于式（3），将 Y-f正交投影到Y+p的空间上，则有正交投影Pm-1为：

2.2 奇异值分解

对投影矩阵Pm进行奇异值分解，则有：

其中，U1=[u1，…，un]和 V1= [v1，…，vn]为酋矩阵，分别包含了 n 个左右奇异值向量；S1=diag｛σ1，…，σn｝为对角矩阵，σi为 S1的第 i个奇异值；U0、V0和 S0为零矩阵。

由文献[19]可知，投影矩阵Pm也可以写成可观矩阵Γm和卡尔曼滤波状态序列的乘积，即：

同样，投影矩阵Pm-1也可以写成如下形式：

其中，Γm-1为Γm去掉最后一行CAm-1后的矩阵。

由式（6）、（7），则可得到可观矩阵 Γm和状态量X^m的表达式：

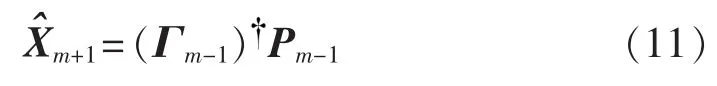
2.3 估计系统矩阵A和输出矩阵C

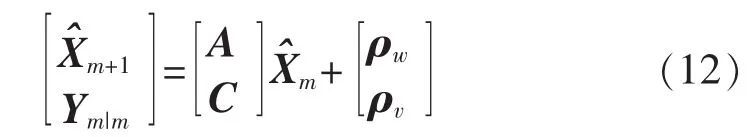
其中，ρw和 ρv为残差向量，与不相关。

利用最小二乘法，定义目标函数为残差，当目标函数最小时，则可以估计出系统矩阵A和输出矩阵C为：

至此，就由已知的观测量Y，得到了随机线性状态空间方程（1）。

3 基于振动数据的风机齿轮箱故障预测

3.1 齿轮箱线性状态空间模型的确立

对于风电机组齿轮箱，由式（4）—（13）可以获得其随机子空间模型。在该过程中，由于利用投影矩阵的定义式（4）和（5）求其值，涉及大维数的矩阵运算，计算量很大。为了避免由定义直接计算投影矩阵Pm，下面给出了简化计算方法。

首先，对量测量 Hankel矩阵式（2）和（3）分别进行LQ分解，得：

然后，计算出 Yp、Yf、Y+p和 Y-f，分别代入投影矩阵的定义式（4）和（5），进行推导得到：

利用式（16）、（17）取代式（4）、（5）计算投影矩阵，也可以避免矩阵的求逆运算。

由于Q1是行正交矩阵，所以矩阵L21的奇异值分解与Pm的奇异值分解具有相同的可观矩阵Γm，证明如下。

投影矩阵为：

其中，Q1为正交阵。

投影矩阵又等于可观矩阵和状态序列的乘积：

若直接对投影矩阵进行奇异值分解，则：

其中，U、V为正交阵；S为对角阵。

联立式（18）—（20）得式（21）：

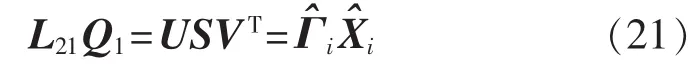
令可观矩阵为：

对式（21）等号两边右乘 QT1，则式（21）转化为：

令 U1=U、VT1=VTQT1，则式（23）变为：

显然U1是正交阵，由于：

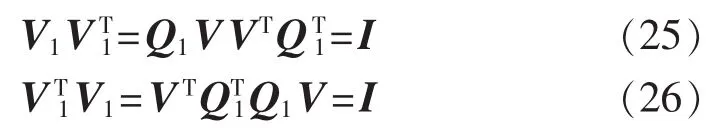
则V1是正交阵；式（24）是关于L21的奇异值分解。令可观矩阵为：则式（22）与式（27）相等，即可观矩阵是相等的。

对L21进行奇异值分解，则有：

因此，利用式（28）可以得到与式（9）相同形式的可观矩阵Γm，而对于状态量，则有：

将可观矩阵Γm上移1行即可获得可观矩阵Γm-1，再利用投影矩阵式（17），可以计算出式（11）的状态量m+1。因此，根据2.3节可以得到齿轮箱随机状态空间模型为：

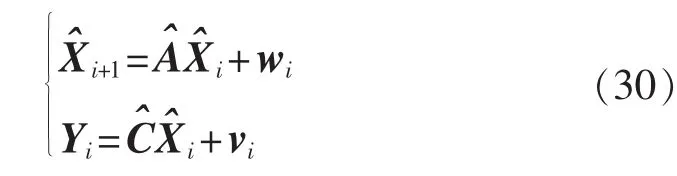
其中，Yi为由振动传感器采集到的振动数据，传感器配置个数决定了Yi的维数；为由2.2节计算出的状态量；与分别为由式（13）计算出的齿轮箱振动状态空间方程的系统矩阵和输出矩阵，是一个方阵，其阶数由奇异值矩阵S1确定，的列数与相同，行数等于振动传感器的个数；wi和vi为噪声。

3.2 齿轮箱故障预测

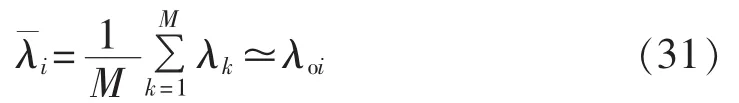
为了有效利用随机子空间模型，需要确定其计算方法的稳定性。判断原则为，即所求系统矩阵的所有特征值均在单位圆以内，则说明该随机模型是稳定的，反之则不稳定。

为了便于比较，引入均方根误差（RMSE）作为评价齿轮箱状态的指标。由于特征值可能为复数，因此定义该指标为：

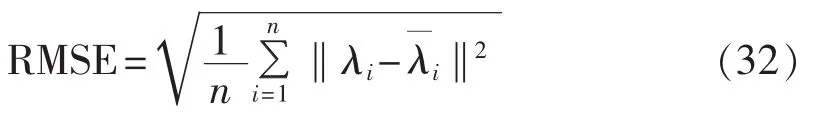
其中，n为系统阶数；λi为由实时振动数据求得的特征值。

3.3 预警值与门槛值的确定

通过定义预警值与门槛值这2个阈值，利用RMSE进行判断，来实现齿轮箱的故障告警和识别。

通过对风电机组齿轮箱振动监测数据进行统计特性分析可知，实时求得的特征值λi散落在参考特征值的附近，误差较小；并对每个实特征值、每个复特征值的实部和虚部与相应的参考特征值的残差进行分析，由分析可知，每个特征值的残差皆为正态分布：

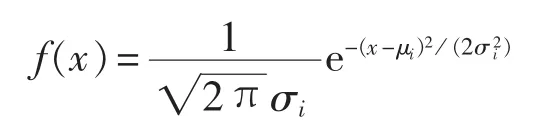
其中，μi为齿轮箱振动信号子空间模型特征值残差的均值；σi为其标准差。因此，可利用统计过程控制（SPC）原理[20]定义齿轮箱故障判别的 2个阈值。

根据SPC原理，服从正态分布的特征值的残差上下限为 si=μi±mσi（m=2，3）。 利用该限值定义齿轮箱故障判别指标RMSE的预警值和门槛值。m=2时，R*定义为预警值，当RMSE超过该值，意味着将要出现故障；而m=3时，R*为故障门槛值，当RMSE超过该值时，则认为已经故障。

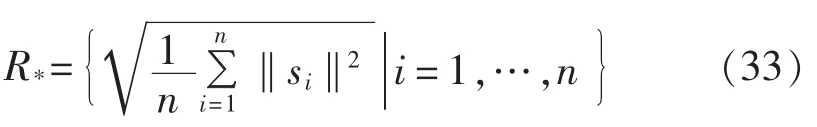
因此，根据实时数据不断计算系统矩阵的特征值和相应的RMSE值，并与所设阈值进行比较，进而可以评估出齿轮箱的运行状态。

4 算例分析

为了充分验证该方法的有效性，对一个实际发生齿轮箱断齿故障的风电机组的振动监测数据进行研究分析。首先，利用该风机齿轮箱故障之前近半年的振动监测数据建立其随机子空间模型，分段计算系统矩阵 A^k；然后，利用所提方法识别系统参考特征值λi；定义齿轮箱故障的判别函数，并确定出相应的阈值，进而就可以实现对齿轮箱的故障预测，具体计算过程如图1所示。

图1 基于子空间方法的风机齿轮箱故障预测算法Fig.1 Gearbox fault prediction algorithm based on subspace method for wind turbine

风电机组容量为1.5 MW，齿轮箱传动结构为2级行星齿轮+1级平行轴，齿轮箱传动比率为100.48；所安装的传感器为加速度传感器，采样率为12 kHz，所采集到的振动信号为相应的加速度信号，单位为m／s2，所分析的正常和异常振动数据如图2所示。

算法中每一段数据窗口的选择应尽可能足够长，以满足子空间方法的参数识别有效性。对该风机齿轮箱的振动监测数据，窗口长度选为6000，其中Hankel矩阵 Yp为 7×5994维矩阵，Yf为 7×5994维矩阵。对形成的测量矩阵进行LQ分解，得到子块矩阵L21，然后利用式（28），对矩阵 L21进行奇异值分解，从而可以确定齿轮箱的随机子空间模型的阶数n为 3，其对应的参考特征值i（i=1，2，3）为：

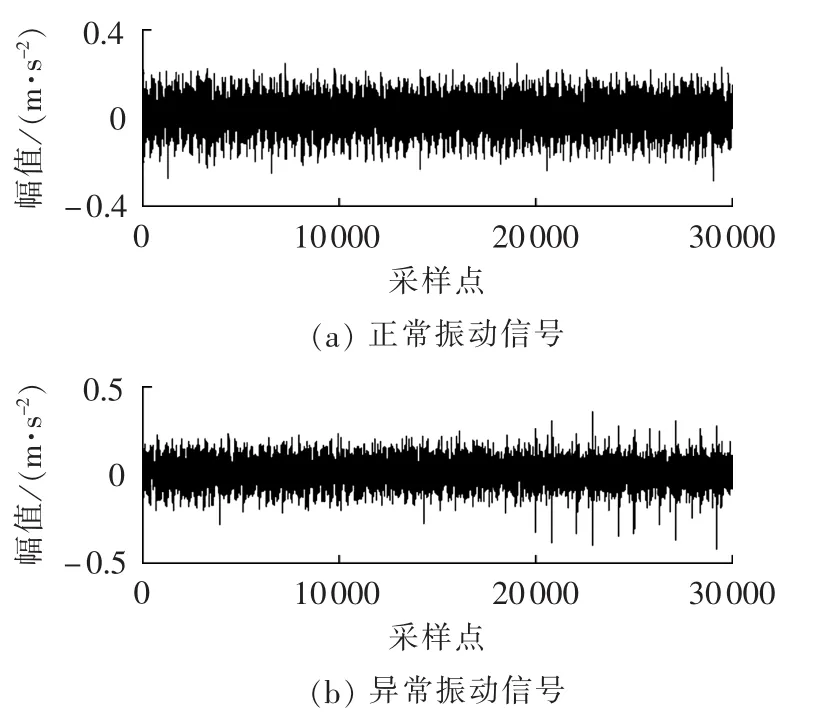
图2 正常与异常状态下的振动信号Fig.2 Normal and abnormal vibration signals

图3给出了参考特征值的分布。从图中可以看出3个参考特征值都分布在单位圆内，说明识别出的齿轮箱随机子空间模型是稳定的。利用稳态运行时的振动采样数据，代入齿轮箱故障判别模型，实时计算出的特征值与参考特征值之间的误差非常小，说明该风机齿轮箱的运行状况很好，是健康的。

图3 齿轮箱正常状态下的参考特征值分布Fig.3 Distribution of reference eigenvalues of gearbox operating in normal state

分析图2中的异常振动信号，其由正常数据和故障数据构成，并从故障前一段时间的振动监测数据开始分析，进行齿轮箱子空间模型的参数计算。通过故障判别指标的计算结果发现，其中1个实数特征值变化不大，但另外2个复特征值逐渐偏离其各自的参考特征值，而且变化趋势逐渐增大，但仍然位于单位圆内。图4给出了各个特征值的演变过程。

为了更加清楚地说明齿轮箱状态的变化过程，利用定义的综合指标分析齿轮箱故障发生的过程。通过对长时间稳态运行的齿轮箱的振动数据的分析，可以计算出各个稳态特征值与相应参考特征值残差的均值μi和标准差σi，并利用SPC原理确定其残差的上下限为 si=μi±mσi，具体计算结果见表1。 再将si代入式（33）中，则可以得到RMSE指标的预警值为0.0084、门槛值为0.0126。

图4 齿轮箱异常状态的特征值分布图Fig.4 Distribution of eigenvalues of gearbox operating in abnormal state

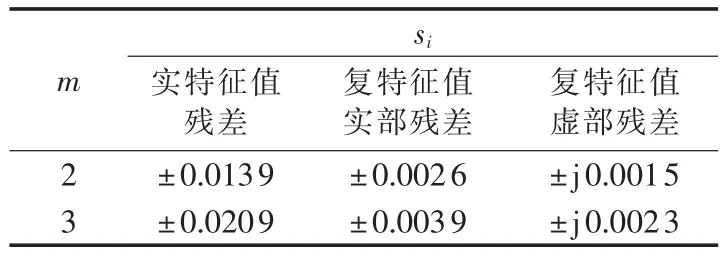
表1 特征值残差上下限Table 1 Upper and lower limits of residual errors of eigenvalues

图5给出了齿轮箱稳态运行时的RMSE指标变化过程（图中每次仿真对应波形上的1个点，图6中同），RMSE值均在预警值以下范围内变化，说明了齿轮箱处于正常运行状态。

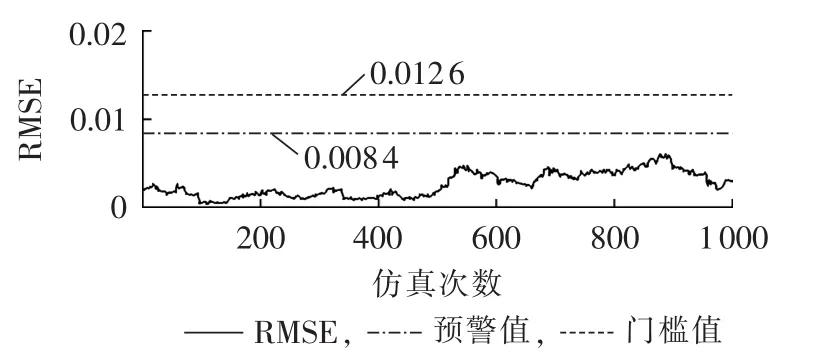
图5 齿轮箱正常状态下的均方根误差变化曲线Fig.5 Curve of RMSE of gearbox operating in normal state

图6 齿轮箱故障过程中的均方根误差变化曲线Fig.6 Curve of RMSE of gearbox operating in abnormal state

图6为齿轮箱故障过程中的RMSE。从图6可以看出，对应图4中的特征值与参考特征值，RMSE出现了越过预警值的情况，甚至最后越过了门槛值。在刚开始的一段RMSE值变化也不大，均在预警值以下，但随着特征值点的发散，RMSE值越来越大；大约在第609个点，曲线越过了预警值0.0084，说明齿轮箱存在异常，有故障的趋势；在第669个点以后，曲线增长到0.0126附近，并且在门槛值附近波动；从第788个点以后迅速上升，且完全越过了门槛值，并且在越限以后曲线继续上升，此时可以认为齿轮箱已经故障。故应该在第609个点到第669个点之间发出预警信号，提醒运行人员采取应对措施。

5 结论与展望

本文提出了一种子空间识别算法，用于仅有观测量已知的风机齿轮故障预测。该算法利用了几何投影的概念，通过投影的行空间可以确定系统的状态量i；通过投影的列空间可以确定系统的可观矩阵Γm；通过对投影矩阵的奇异值分解可以确定系统的阶数n，进而可以确定系统矩阵的维数，并计算相应的特征值和RMSE指标，以实现齿轮箱运行状态的评估。

通过对振动数据的仿真分析，可以得出以下结论：首先，由该随机子空间算法识别出的随机状态空间模型具有良好的稳定性；其次，当已知参考特征值后，可以用其作为评判齿轮箱状态的一个直观参考；最后，引入了RMSE指标对各个特征值的分布情况进行定量评价，当齿轮箱处于不同运行状态时，通过该故障预测算法给出的相应RMSE变化趋势，可以对齿轮箱进行故障预测，给现场监测和制定检修计划提供一定的指导，在提高风电机组的经济性和可靠性方面具有重要意义。

本文所提方法虽然能够预测出故障的发生，但在识别出具体故障方面还需要完善。将继续从两方面对该算法进行深化研究：一是研究子空间算法中特征值与故障类型之间的关系；二是研究子空间与频谱分析相结合的故障预测方法，以实现风电机组齿轮箱的故障识别。