定子双绕组风力感应发电机优化设计方法
韩 力,罗张尧,2,金 钊,袁 春,卢 彬,潘小兵
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.国家电网重庆市电力公司万州供电分公司,重庆 404000;3.重庆通信学院 军用特种电源军队重点实验室,重庆 400035)
0 引言
定子双绕组感应发电机DWIG(Dual stator-Winding Induction Generator)是一种励磁无功连续可调的新型交流电机,它不仅继承了笼型转子感应电机结构简单、运行可靠、维护方便等优点,而且克服了传统感应发电系统电力电子装置容量和体积大、谐波成分大等缺陷,在独立电源和风力发电领域具有广阔应用前景[1-3]。
目前,DWIG在电磁设计及无功功率容量优化方面已取得了一定的研究成果[4-7]。励磁变换器容量对风力DWIG系统成本和体积有重要影响,而控制绕组电流在发电机变速运行过程中的最大值反映了励磁变换器的容量[4]。为此,文献[4-5]通过励磁电容的优化选取,实现控制绕组电流在整个变速范围内的最大值最小,以达到励磁变换器容量最小化的目的,但研究是在电机本体参数固定不变的情况下进行的。然而,对DWIG电机本体参数和励磁电容进行一体优化的文献还不多见。文献[6]和[7]分别采用粒子群优化 PSO(Particle Swarm Optimization)算法和改进的遗传算法GA(Genetic Algorithm),对应用于独立电源系统的DWIG进行了优化设计,但该研究主要针对额定转速及以上且输出功率保持恒定的工况进行的,未讨论额定转速以下的工况。此外,文献[6]中的PSO算法具有容易早熟收敛的缺点,文献[7]从自身参数调整的角度出发进行GA改进,这不能较大程度地改变GA收敛速度慢的缺点;其次,文献[6]、[7]的优化变量个数分别仅有7个和9个,相对较少。因此,有必要针对风力DWIG进一步开展电机本体参数和励磁电容一体优化的研究。
随着优化技术的发展,PSO算法以其概念简单、收敛速度快、易于编程等特点在电机优化设计中应用广泛。然而,该算法存在早熟收敛的问题,尤其在复杂多峰问题中表现较为明显[8]。在对PSO算法进行的各种改进中,混合算法成为改进研究中很重要的一个分支,具有较高的研究价值和较好的应用前景[9]。与此同时,近年来基于Memetic思想的算法研究成为进化计算的一个研究热点[10],它体现了一种更为广义的混合优化思想,从一定程度上对现有混合算法的研究思路进行了补充和完善[11]。相对于传统两两优势互补相结合的思路而言,它提供了一种更为广阔的综合算法思路。基于该思想,可进一步开展对DWIG优化算法的研究工作。
为此,本文以笼型转子结构的DWIG为研究对象,首先分析风力DWIG的特点,其次根据风力发电的特点建立优化设计模型,然后基于Memetic算法思想提出具有向成功和失败双重学习能力的遗传-粒子群综合算法GPSMA(Genetic-Particle Swarm Memetic Algorithm),最后运用GPSMA对一台18.5kW的DWIG样机进行优化设计,并对优化方案进行分析。
1 风力DWIG的特点
1.1 系统结构及输出功率特点
风力DWIG系统主要包括DWIG本体、风力机、齿轮箱、励磁变换器和励磁电容、整流桥等其他辅助设备,系统结构如图1所示。该发电系统既可直接为直流负载供电,也可通过逆变器为交流负载供电。DWIG的转子为普通笼型转子结构,但其定子上有2套极对数相同的绕组:一套为功率绕组,输出端接负载;另一套为控制绕组,接有静止的励磁变换器,由变换器提供DWIG所需的励磁无功功率,采用一定的控制策略,可有效调节功率绕组使之输出恒幅值的电压。
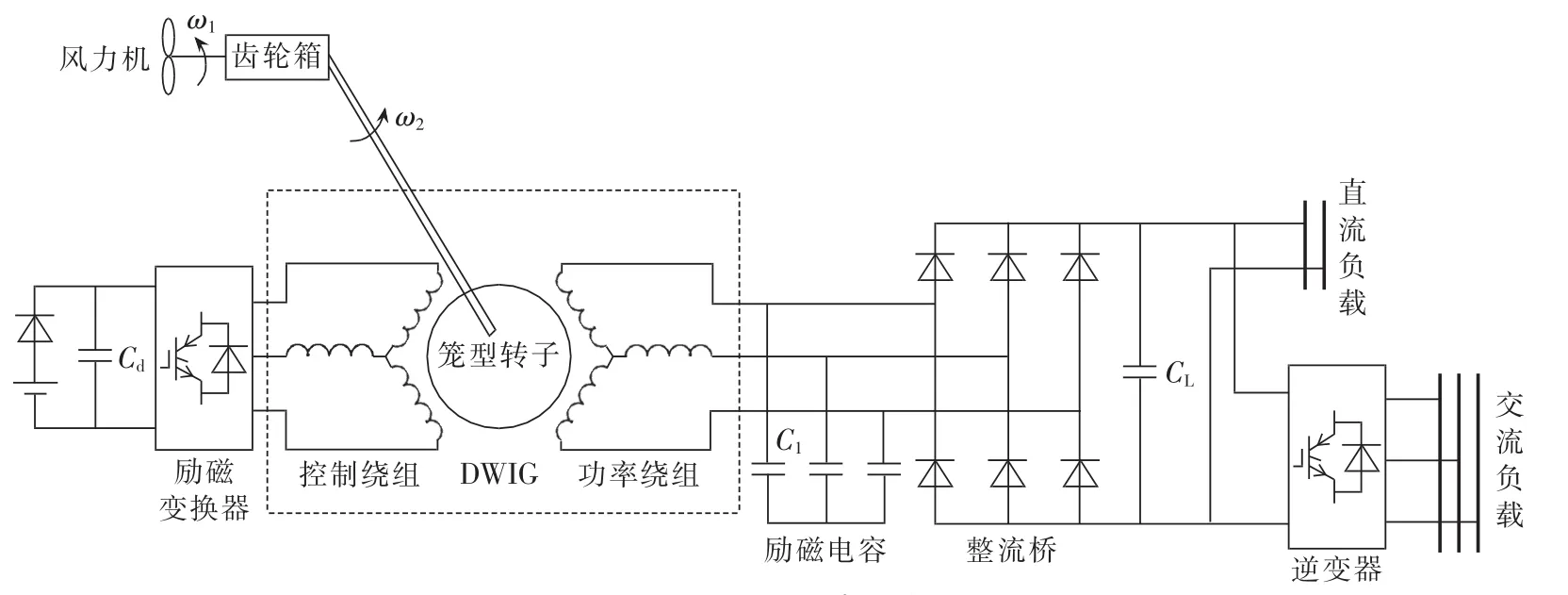
图1 DWIG系统结构Fig.1 Structure of DWIG system
针对变速运行的风力DWIG系统,假设在额定风速以下,采用最大风能追踪控制策略来实现风能的最大捕获;在额定风速以上,采用变桨距角控制策略来限定风力机的输出功率,从而使DWIG输出功率P2保持恒定[12]。参考文献[5]中DWIG输出功率的变化规律,当转速n小于额定转速nN时,DWIG的P2与n3近似成正比关系;当n大于nN时,P2维持额定输出功率P2N不变。设DWIG的转速范围为1100~2000 r/min,额定转速为 1500r/min,额定功率为 18.5kW,在理想控制策略下的DWIG输出功率曲线如图2所示。
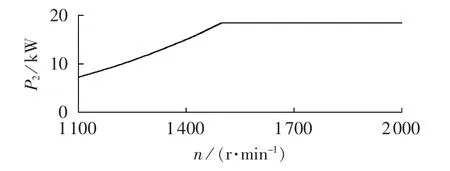
图2 DWIG输出功率与转速关系Fig.2 Relationship between output power and speed of DWIG
1.2 电磁设计特点
由于DWIG结构和普通笼型转子感应电机结构类似,其电磁设计可参考常规感应电动机的电磁设计流程,但也具有其自身特点。
a.电动势系数的计算。DWIG感应电动势要大于电动机运行时的值,且电动势系数会随工作点的不同而发生变化。在迭代计算时取大于1的值,一般在1.05~1.1范围内。
b.功率绕组电流的计算。与同步发电机不同,DWIG功率绕组电流大小是未知的,它与负载电流及流过励磁电容的电流有关。本文通过下式来确定功率绕组电流及功率因数。

其中,Ip和Ipl、Ipc分别为功率绕组电流及其有功、无功分量;φp为功率绕组的功率因数角;IL和φL分别为负载电流和负载功率因数角;ω为功率绕组电流角频率;C1为励磁电容;Up为功率绕组电压。
c.控制绕组电流的计算。DWIG通过对控制绕组电流的控制来实现励磁无功的调节,达到功率绕组恒压输出的目的。因此,控制绕组电流值对恒压输出性能有直接影响。另外,控制绕组电流值也是励磁变换器容量选取的重要依据。所以,控制绕组电流的计算具有重要意义,它体现了DWIG励磁无功调节的特点。文献[13]对不同负载下的控制绕组电流计算方法进行了推导,得到:
其中,Em和Xm分别为激磁电动势和激磁电抗;Ic为归算到功率绕组侧的控制绕组电流;Xp和Rr、Xr分别为功率绕组漏抗及归算到功率绕组侧的转子电阻、漏抗;s为转差率;当 Ip呈容性时“∓”中取“-”号,当 Ip呈感性时“∓”中取“+”号。
d.转差率的计算。与感应电动机不同,处于发电状态的DWIG转差率为负值,迭代计算时可预取为 -0.02~-0.01范围内,其计算方法可参考下式[13]:

其中,Pe为电磁功率。
e.定、转子槽型及绕组布置。定子采用圆底槽,其中嵌放功率绕组和控制绕组。为降低功率绕组漏抗,将功率绕组放置于槽上层。转子为普通铜条笼型转子结构,采用梯形槽。
基于以上分析,通过Visual Basic 6.0平台编制DWIG电磁设计程序,其流程如图3所示。在电磁设计中,以Y180M-4感应电动机为原型,得到一台18.5 kW的DWIG初始设计方案,如表1所示。

图3 DWIG电磁设计流程图Fig.3 Flowchart of DWIG electromagnetic design
1.3 励磁电容对风力DWIG的影响
由式(1)、(2)可知,控制绕组电流与励磁电容、电机本体参数均紧密相连,在优化设计中应充分考虑。在表1中初始方案所给发电机本体参数的基础上,当励磁电容取不同值时,得到的控制绕组电流随转速的变化曲线如图4所示。控制绕组电流为正时表示补偿无功,为负则表示吸收多余无功。在整个变速运行区间内,控制绕组电流的最大值Ic(max)和最小值Ic(min)分别出现在最低转速和最高转速处。
在励磁电容 C1由 150 μF变化到 350 μF的过程中,控制绕组电流的最大值Ic(max)由32.1 A减小到18.5 A,控制绕组电流的最小值 Ic(min)由 9 A变化到 -8.3 A。 即 Ic(max)随 C1增加而减小,当 C1增加到一定程度使得 Ic(min)小于 0 时 ,随C1增加而增大。为了使励磁变换器的容量最小,意味着整个变速范围内应使最大值最小。结合图4及其数据分析可见,当改变励磁电容 C1使得到满足时,可实现整个变速范围内经过励磁变换器的最大电流值最小。综合考虑励磁电容变化对励磁变换器容量和电机性能影响,本文选取C1=300 μF作为DWIG优化设计初始方案中的励磁电容的参考值。
2 DWIG优化设计模型
DWIG的优化设计属于强耦合、非线性、多峰值的复杂优化问题。针对风力DWIG的特点,其优化设计模型可表示为:

表1 设计方案对比Table 1 Comparison of design schemes

图4 控制绕组电流随转速变化曲线Fig.4 Curve of control winding current vs.speed for different excitation capacitances
其中,f(X)为目标函数;X 为优化变量;gi(X)为约束函数;m为约束条件个数。
2.1 优化目标
考虑到风力DWIG需满足在变速范围内控制绕组电流小[6]、效率高的要求,本文分别选取变速范围内控制绕组电流最大值最小、额定效率ηN最高作为优化目标。
a.以控制绕组电流为优化目标。
为了实现励磁变换器的容量最小,应满足Ic(max)=。当把发电机参数和励磁电容进行整体优化时,控制绕组电流的变化规律仍与上述情况一致。因此,在DWIG的优化设计中,可选取控制绕组电流作为优化目标函数,如式(5)所示。

b.以额定效率为优化目标。
由于优化目标是求额定效率的最大值问题,为便于求解,本文将其转换为最小值问题的求解,因此优化目标函数取为额定效率ηN的负数。通过该优化目标的选取,可提高DWIG的额定运行效率。

2.2 优化变量
为了提高优化效果,应尽可能多地考虑对发电机性能影响较大的设计变量。经综合分析,本文选取DWIG的铁芯长度 Lt、定子内径 Di1、气隙长度 δ、功率绕组每线圈匝数Np、控制绕组每线圈匝数Nc、功率绕线径dp、控制绕组线径dc、定子槽肩宽b11、转子槽肩宽 b12、定子槽高h21、转子槽高h22、定子槽底半径r21、转子槽底宽b22以及励磁电容C1共14个参数作为优化变量。
2.3 约束条件
电机优化设计的约束条件主要指电机的制造工艺限制和技术性能要求,主要包括结构参数约束和性能参数约束两大类。参考其他类型电机的设计数据和经验[14],并结合DWIG的自身特点,本文约束条件设置如下。
a.定、转子齿磁密 Bt1、Bt2及轭磁密 Bj1、Bj2限定为0.8~1.6 T,气隙磁密 Bδ限定为 0.5~0.8 T。
b.功率绕组输出功率P2满足图2的变化规律。
c.功率绕组电流密度Jp限定为4~6.5 A/mm2。考虑到变速运行时,某一转速下可能只需很小的控制绕组电流即可实现恒压输出,因此控制绕组电流密度Jc限定为0~6.5 A/mm2;转子导条和端环电流密度 Jb、Jr分别限定为 2~5 A /mm2和 0.9~4 A /mm2。
d.槽满率Sf限定为70%~80%。
e.由于部分优化变量是离散的,如铁芯长度、线圈匝数、绕组线规等。在优化过程中,这部分变量需按照离散变量的最小单位或相关要求进行转换。本文中,铁芯长度最小单位取5 mm,线圈匝数最小单位取1,绕组线径则转换成标准线规。
f.为保证经过优化设计的DWIG有较高的效率,本文在以控制绕组电流为优化目标时,限定最低额定效率为89%。
3 GPSMA
3.1 PSO算法
Kennedy等人于1995年提出了PSO算法的最初版本,其后Shi等人引入了惯性权重对算法进行了改进,形成了当前的标准版本[15]。
假定粒子群由N个粒子组成,粒子的信息用D维向量表示,第 i个粒子位置表示为 xi=(xi1,…,xid,…,xiD)T,速度为 vi= (vi1,…,vid,…,viD)T,个体极 值pbesti=(pbesti1,…,pbestid,…,pbestiD)T,全局极值 gbest= (gbest1,…,gbestd,…,gbestD)T。
在每次迭代计算过程中,粒子速度和位置分别按照式(7)、(8)进行更新。
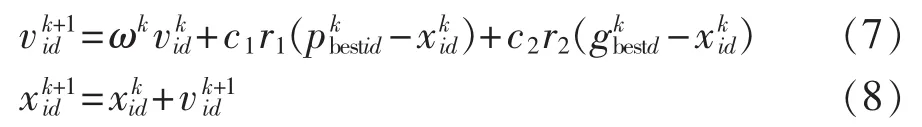
其中,k为当前迭代次数;r1和 r2为[0,1]之间的随机数;ωk为第k次迭代的惯性权重;c1、c2分别为个体学习因子和社会学习因子;vkid、vk+1id和xkid、xk+1id分别为第k次和第k+1次迭代时第i个粒子速度和位置的第d维分量;为第k次迭代时第i个粒子个体极值点位置的d维分量;为第k次迭代时粒子群的全局极值点位置的d维分量。
3.2 GPSMA思想
由于PSO算法具有收敛速度快的优势,本文以PSO算法为主体构架展开综合算法的探讨,期望获取能较好克服早熟收敛缺陷且收敛速度较快的Memetic算法。
PSO算法基于“个体认知”和“向群体中优秀个体学习”的思想去寻找最优解,因此收敛速度快的同时也就容易丢失种群的多样性。而GA具有的遗传操作中的交叉和变异操作能较好地保持种群的多样性;但单纯引入交叉、变异操作虽然可增加种群多样性,但也可能破坏优秀个体。因此,本文提出的算法宜选取一定量的优秀粒子直接进入下一代;与此同时,虽然实际中大多强调向优秀个体(成功经验)学习的重要性,但不能否认,在成长过程中也同样需要从失败中获取经验教训。例如爱迪生从多次失败的实验中积累经验,终于成功发明了灯泡,为黑夜带来了光明。鉴于此,本文提出的GPSMA可引入该思想,对于适应度值较差的粒子,采用从失败中获取经验的方法,使其远离粒子自身和整个群体曾找到的最差位置。
文献[16]指出,在实际中由于食物匮乏或过于拥挤等原因,将使觅食的鸟群不断进行分散和重组。据此,该文提出了振荡参数策略OPS(Oscillating Parameter Strategy),该策略通过对PSO算法惯性权重及学习因子的振荡,使全局搜索和局部挖掘在整个优化过程中交替进行。试验证明,该策略能从一定程度上增强算法的全局搜索和局部挖掘能力。结合生物背景,本文提出的GPSMA也可借鉴这一思想,对收敛过程中的惯性权重和学习因子进行振荡操作。
综上所述,现提出具有双重学习能力的GPSMA思想如下:以PSO算法构架为主体,在运算过程中引入遗传操作,为防止遗传操作对优秀个体的破坏,选取部分优秀粒子直接进入下一代;与此同时,对适应度值较差的个体,采用向失败学习的策略,这样可实现粒子群向成功和失败的双重学习功能,达到开发较差个体“潜力”的目的。从理论上分析,上述操作能在保证下一代粒子质量的同时减少粒子陷入局部最优的可能。在算法参数调整方面,采用OPS加强算法的全局搜索和局部挖掘能力。
3.3 GPSMA模型
GPSMA流程描述如下:
a.根据给定变量的初始范围,初始化粒子群P,随机产生每个粒子的初始速度和位置;
b.计算每个粒子的适应度值,确定粒子群中的个体最优值和全局最优值;
c.若满足终止条件则寻优结束,否则继续;
d.将粒子群P中的N个粒子按式(9)—(13)进行交叉、变异操作,生成新个体并保存到数组Q1中,单次迭代中共进行N/4次遗传操作,共生成N/2个新粒子;
e.将P中适应度值较差的N/2个粒子保存到数组 Q2中,让 Q2中粒子按式(14)、(15)向失败学习;
f.将Q1、Q2中粒子合并为种群P1,此时P1中粒子数与原种群相同,为N;
g.计算P1中粒子适应度值,并选取P1中适应度值较好的N/2个粒子替换原粒子群P中适应度值较差的N/2个个体;
h.对粒子群P按式(16)—(18)更新粒子的惯性权重和学习因子,按式(7)、(8)更新粒子速度和位置;
i.跳转至步骤b,继续寻优直到满足终止条件为止。
在迭代过程中,交叉运算按式(9)—(11)进行,变异运算按式(12)、(13)进行[17]。
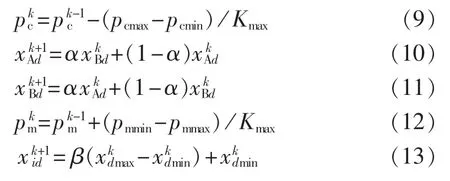
其中,pc、pcmax和pcmin分别为交叉概率及其初值和终值;Kmax为最大进化代数;xAd和xBd分别为交叉操作的两个体的d维分量;α、β均为[0,1]之间的随机数;pm、pmmin和pmmax分别为变异概率及其初值和终值。
记个体最差值为 pworsti=(pworsti1,…,pworstid,…,pworstiD)T,全局最差值为 gworst= (gworst1,…,gworstd,…,gworstD)T,较差粒子更新过程如下[18]。

每次迭代过程中的 OPS 如下[16]:

其中,ωmax、ωmin分别为每个振荡周期的惯性权重初值和终值;c1k、c2k分别为第k次迭代时个体学习因子和社会学习因子;c1max、c1min分别为每个振荡周期的个体学习因子初值和终值;c2min、c2max分别为每个振荡周期的社会学习因子初值和终值;mod为取余运算;KSI是每个振荡周期的迭代次数。
在迭代过程中,惯性权重和学习因子的振荡情况如图5所示。

图5 PSO参数振荡过程Fig.5 Oscillation of PSO parameters
3.4 性能比较
为了验证GPSMA的有效性,选用4个典型的Benchmark函数对其进行分析。表2给出个4个函数的定义及搜索空间,表中D为变量维数,各函数的全局最优值均为0。

表2 测试函数Table 2 Benchmark functions
在此基础上,选择实数编码遗传算法RGA(Realcoded Genetic Algorithm)、标准PSO算法、带振荡参数策略的粒子群优化(OPS-PSO)算法与GPSMA进行性能比较。参考文献[16],各算法参数设置见表3。

表3 不同算法参数设置Table 3 Parameter settings for different algorithms
考虑到DWIG的优化变量有14个,为了对比分析GPSMA的有效性,这里研究维数D=20情况下不同算法的收敛性。由于遗传操作主要是保持种群的多样性,本文赋予较大的交叉和变异概率;由3.3节的算法流程可知,GPSMA在1次迭代中对N个粒子进行了2次适应度值评价操作,而其余3种算法则仅对N个粒子的适应度值评价了1次。为保证对不同算法性能评价的公平性,在4种算法总评价次数相同的情况下来探讨不同算法的寻优效果,即GPSMA的迭代次数为其余3种算法的一半。另外,对于简单函数f1(x),试验中,除RGA之外,其余3种算法在评价次数为1500次时均能达到较好的寻优效果。但本文为评价次数的表示方便,各算法对函数f1(x)的迭代次数设置分别与其余3个测试函数相同。
分别对4个测试函数进行30次试验,GPSMA的终止条件为达到最大迭代次数3000,其余3种算法的终止条件为达到最大迭代次数6000。试验结果如表4所示。由此可见,对于函数f1(x),除了RGA,其余3种算法在达到相应迭代次数之后表现都不错,虽然GPSMA的各项指标均低于PSO算法和OPS-PSO算法,但从优化结果的数量级而言,其寻优效果与PSO算法、OPS-PSO算法近似;对于函数f2(x),GPSMA和OPS-PSO算法的各项指标均在较大程度上优于RGA和PSO算法,虽然GPSMA的最优解比OPS-PSO算法略差,但平均解和最劣解均优于OPSPSO 算法;对于函数 f3(x)和 f4(x),GPSMA 的各项指标明显优于其余3种算法,RGA次之,PSO算法和OPS-PSO算法最差。

表4 不同算法的寻优效果Table 4 Optimization effects of different algorithms
综上所述,GPSMA对于多峰复杂函数 f3(x)、f4(x),其寻优效果相比另外3种算法都有较大程度的提高。这主要是由于保持种群多样性的遗传和向失败学习的操作能较好地帮助该算法跳出局部最优陷阱。数值试验较为客观地验证了GPSMA的有效性。因此,GPSMA更适用于具有多变量、多峰值、非线性的DWIG优化问题的研究。
4 优化设计实例
根据DWIG优化设计模型,利用DWIG电磁设计程序与GPSMA,得出DWIG优化设计程序,其流程如图6所示。

图6 DWIG优化设计程序流程图Fig.6 Flowchart of DWIG optimal design
在此基础上,对表1中初始方案所示18.5 kW的DWIG样机进行优化设计。假设DWIG变速范围为1100~2000r/min,在理想控制策略下输出功率满足图2所示的变化规律,转速变化过程中负载功率因数cosφL=0.95(滞后)保持不变,输出电压 400 V,杂散损耗和机械损耗之和保持252 W不变。GPSMA参数设置时,除D=14外,其余参数设置与表3相同。优化设计终止条件为:目标函数值的误差连续50次迭代小于0.1%或单次优化中迭代次数大于1000。
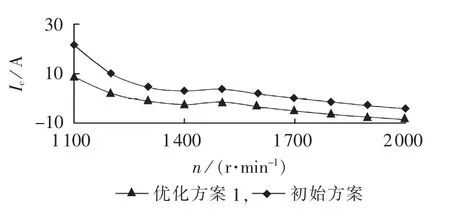
图7 不同设计方案下控制绕组电流随转速变化曲线Fig.7 Curve of control winding current vs.speed for different schemes

图8 不同设计方案下效率随转速变化曲线Fig.8 Curve of efficiency vs.speed for different schemes
由表1可知,各套方案均满足约束条件,且性能参数都在合理范围之内。相对于初始方案,优化方案1中的最大值减小了62.7%,优化方案2中额定效率提高了0.94%。
由图7可知,优化方案1在最低转速和最高转速时的控制绕组电流绝对值相等,且在整个变速范围内的最大值较小。由于励磁变换器容量与输出总功率的比值等于控制绕组和功率绕组的容量比,参考文献[19]的方法,2套绕组的容量比可采用下式进行估算。

据此计算出初始方案和优化方案1的容量比Kv分别为72.8%和26.5%,由此可知,优化方案1较好地达到了减小励磁变换器容量的目的。此时,励磁变换器容量约为额定输出功率PN的31.2%。文献[5]对一台37kW的DWIG经过励磁电容的优化选取之后,励磁变换器容量与输出功率之比为31%,本文结果与之基本相当,从而间接验证了本文优化模型与设计方案的正确性和有效性。
由图8可知,优化方案2在每个转速下的效率均高于初始方案,整个变速范围内效率的平均值相对于初始方案提高了1.4%。在转速增加的过程中,效率呈先增大后减小的趋势,这与文献[12]实验测得的结果一致,从而间接验证了本文研究结果的正确性。
5 结论
在兼顾励磁变换器容量与额定效率的情况下,本文从励磁电容和电机本体参数一体优化的角度出发,分析并建立了DWIG的优化设计模型,分别以控制绕组电流最小、额定效率最高为优化目标,提出了14个优化变量,并给出了相应的约束条件。同时,提出了一种适用于多变量、强耦合、非线性、多峰值函数优化的GPSMA,并通过数值试验验证了该算法的有效性。最后,采用该算法对一台18.5 kW的DWIG样机进行了优化设计,相对于初始方案得到如下结论:优化方案1控制绕组电流最大值减小62.7%,2套绕组的容量比由72.8%降低到26.5%;优化方案2额定效率提高了0.94%,变速范围内效率的平均值提高了1.4%。下一步的工作是准备通过实验来进一步验证模型和算法的正确性。

