正项级数比较判别法中“参照级数”的碎片化*

闻道君，陈义安(重庆工商大学数学与统计学院，重庆400067)

正项级数比较判别法中“参照级数”的碎片化*

闻道君，陈义安
(重庆工商大学数学与统计学院，重庆400067)

在MOOC模式下将无穷小量的阶与无穷级数比较判别法的极限形式结合起来，通过无穷级数通项对应的等价(或同阶)无穷小量、高阶无穷小量和低阶无穷小量来寻找适当的“参照级数”，解决了正项级数比较判别法的碎片化与知识系统性问题，并举例说明该方法在判定无穷级数收敛性方面的的有效性.

正项级数;比较判别法;无穷小量;p－级数;收敛;MOOC;知识碎片化

最近，MOOC(Massive Open Online Course，大规模公开在线课程，中文又称“慕课”)以一种引人瞩目的方式成为世界高等教育领域的热词和流行语，活跃于各大纸质媒体大学的版面上，刮起了一轮席卷全球的线上教育热潮.“MOOC”以世界一流大学最优质的教学资源为基础，以现代最先进的信息技术为支撑，以微视频、学习大数据、个性化学习等最新的教学理念为指导，以“短视频(一般10 min左右)+交互式练习(interactive exercises)”为基本教学单元的知识点/知识体组织模式和学习模式.这就要求将知识的颗粒度做到比较小，便于“碎片化”学习，也有利于学生记忆与理解.这些“碎片化”的基本教学元素构成了一个动态可控的有机体，使得各种优质的学习材料在在线学习过程中被及时调动起来，学生对学习进度具有一定的主动性和控制权.同时，MOOC课程的学习者很可能是社会上的海量人群，不具有校内课堂教学秩序的节奏性、可控性和相对独立性.课程的教学体系的改革和知识“碎片化”方式也必须面对这一开放性的学习对象，研究课堂教学知识的“缺失”到“价值回归”，探寻将“专业知识”转化为面向学生“教学知识”的方法，以及如何将知识“碎片化”，并防止“碎片化”导致的学术严谨性不足，确保课程知识系统化教学目标的完成就显得举足轻重.

另一方面，高等数学是高等院校的公共基础课程，几乎涉及高等院校的所有学科和专业，无穷级数是高等数学中的重要组成部分.关于正项级数的敛散性的判别方法主要有比较判别法、比值判别法和根式判别法，其中应用最广泛的是比较判别法及其极限形式，这也是高等数学教学的重点和难点.运用正项级数比较判别法或其极限形式，最困难的是寻找一个适合的“参照级数”，并通过其已知的收敛性进一步判定原级数的收敛性［1－4］.由于比较判别法中包含了两类失效的情形，即通项比收敛级数更大的和比发散级数更小的级数是无法判定其收敛性的，但是这并不意味着无穷级数的收敛性不能确定，很可能是因为选择了不适当的级数进行比较，所以“参照级数”的选择在无穷级数收敛性的判定中就显得至关重要了.根据多年的教学经验，通过引入等价无穷小量的方法寻找有效的“参照级数”，在一定程度上解决了比较判别法的碎片化与系统性问题.同时，当等价无穷小量的获得变得比较困难时，可进一步借助高阶无穷小量、低阶无穷小量和p－级数、几何级数对无穷级数的收敛性进行判定，极大地简化了无穷级数的比较判别法极限形式的理解和应用.

1　预备知识

定义1设实数序列u1，u2，u3，…，un，…，称u1+u2+u3+…+un+…为常数项无穷级数，简称级数，记为，其中称un为通项或一般项.如果un≥0，称为正项级数;级数的前n项和Sn=u1+u2+u3+…+un，称为级数的部分和.

引理1［1，2］(收敛的必要条件)设无穷级数收敛，则limun=0.n→∞

引理2［1，2］(比较判别法)设为正项级数，且满足un≤vn(n=1，2，..)，则

引理3［1－3］(比较判别法的极限形式)设为正项级数，且，则

2　教学难点及方法

3　应用举例

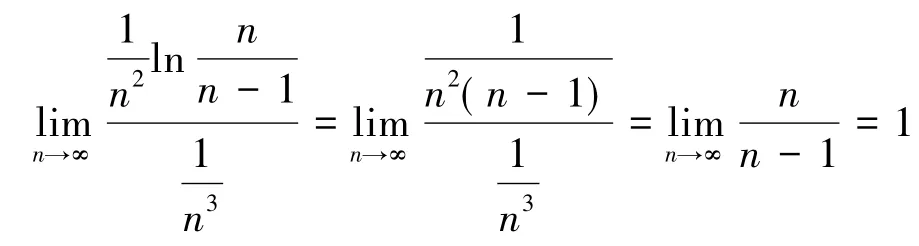
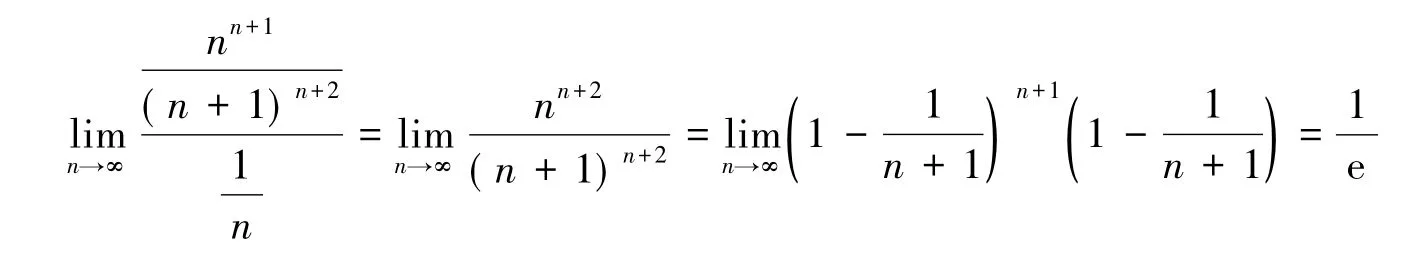
解由于

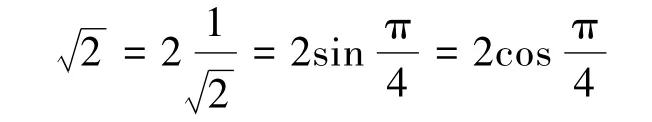
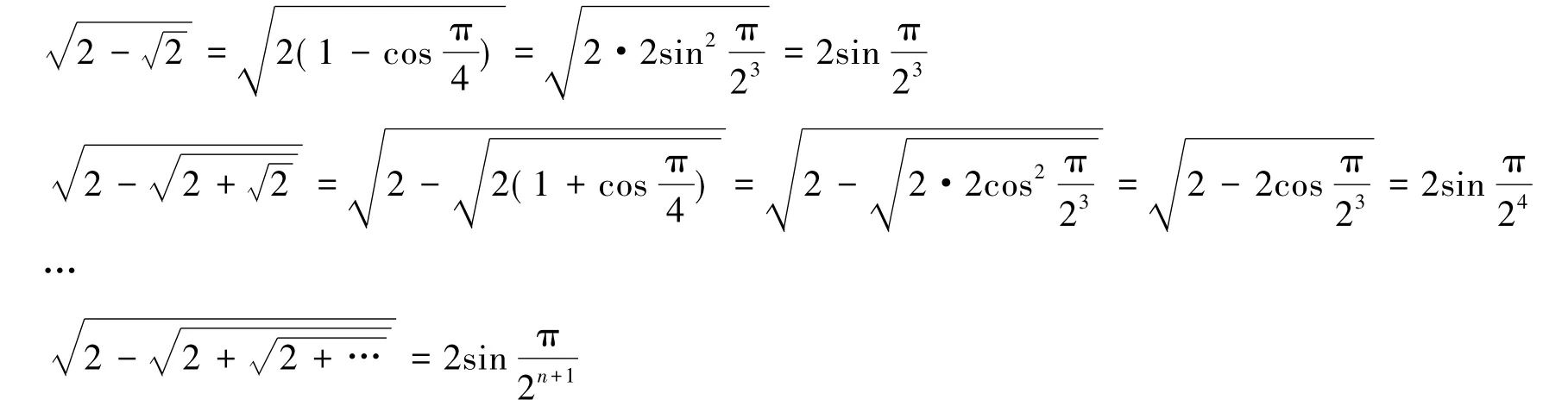
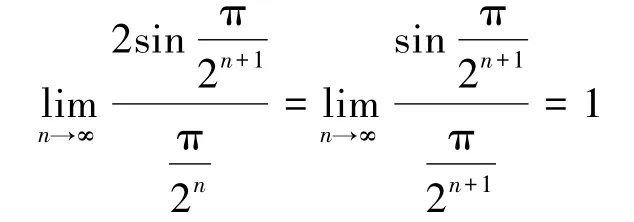
［1］龚德恩，范培华.微积分［M］.北京:高等教育出版社，2008

［2］陈修素，陈义安，雷澜，等.微积分(下册)［M］.北京:高等教育出版社，2011

［3］陈文灯，袁一圃，俞元洪.高等数学复习指导［M］.北京:北京理工大学出版社，1992

［4］陈传璋，金福临，朱学炎，等.数学分析［M］.2版.北京:高等教育出版社，1995

［5］闻道君，龚黔芬.Simpson不等式的改进及其应用［J］.数学的实践与认识，2010，40(21):159-162

［6］闻道君，陈义安，唐艳.高等院校经管类专业的数学教学方法研究［J］.重庆工商大学学报:自然科学版，2011，28(4): 413-416

［7］李红婷.高师“数学教学论”课程建设的反思与重构［J］.西南师范大学学报:自然科学版，2010，35(6):196-200

［8］江蓉，王守中.矩阵的秩在线性代数中的应用及其教学方法的探讨［J］.西南师范大学学报:自然科学版，2012，37(8): 175-180

［9］闻道君，唐艳，陈义安.支架式教学:一个重要极限的抽象方法究［J］.重庆工商大学学报:自然科学版，2014，31(10):78-80

Fragmentization of“Reference Series”of Comparing Discriminant Methods for a Positive Term Series

WEN Dao-jun，XIA Li，CHEN Yi-an
(College of Mathematics and Statistics，Chongqing Technology and Business University，Chongqing 400067，China)

This paper combines the order of infinitesimality with the limiting form of comparing discriminant methods for a positive term series under themodel of MOOC.A proper“reference series”is found by equivalent(or same order)infinitesimality with original series，or high-order or low-order infinitesimality respectively which general term corresponds to.The problem of fragmentization and knowledge systematicness of the comparing discriminantmethods for a positive term series is solved.Moreovr，the effectivity of this method is illustrated by some instances in discriminating the convergence of infinite series.

positive term series;comparing discriminant methods;infinitesimality;p-series;convergence; MOOC;knowledge fragmentization

0173.1;G420

A

1672－058X(2015)09－0071－05

10.16055/j.issn.1672－058X.2015.0009.018

2014－12－26;

2015－03－09.

重庆市高等学校教学改革研究项目(143059);重庆市教育科学规划课题(2014－GX－097);重庆工商大学教育教学改革研究项目(130224).

闻道君(1975-)，男，四川内江人，硕士，副教授，从事不动点理论与经济数学基础课程的教学研究.