从三个角度考察柯西不等式

咸伟志(重庆师范大学数学学院，重庆401331)

从三个角度考察柯西不等式

咸伟志
(重庆师范大学数学学院，重庆401331)

柯西不等式是高等数学中的重要不等式，它在解析几何、数学分析与高等代数这3门数学专业主干基础课程中均有渗透.从这3门课程的角度，分别给出柯西不等式的不同形式和证明过程，并简要地阐述它们的联系，最后做出小结.

柯西不等式;数量积;定积分;欧氏空间;内积

解析几何、数学分析和高等代数是大学数学类专业的3门主干基础课程，即通常所说的“三高”课程.虽然“三高”课程的理论不同，处理问题的思想方法也不同，但它们也能相互联系，相互渗透，从不同的角度诠释同一件事物，如点到平面的距离公式［1］.事实上，著名的柯西不等式是一个很好的例证，尽管它在“三高”课程中的表现形式不同，证明方法不同，但本质上具有很强的联系和一致性，下面将分别论述.对于柯西不等式的3种形式，其证明过程所涉及的内容均作为预备知识提出，不再赘言.

1　解析几何的角度

1.1相关预备知识

定义1［2］两个向量和的模和他们夹角的余弦的乘积叫做向量和的数量积，记.特别地

定理1［2］(数量积的坐标表示公式)在直角坐标系O－xyz中，向

1.2柯西不等式在解析几何中的形式及证明

注1:令a3=b3=0，则得到形式Ⅰ的二维形式.

形式Ⅰ的证明从三维空间向量的角度使得对柯西不等式有了较为直观的理解.事实上，受形式Ⅰ的启发，利用数学归纳法，可得到解析几何角度下不等式的推广形式:

证明①当n=1，2，3时，结论已成立.

②假设当n=k(k≥3)时，结论成立.

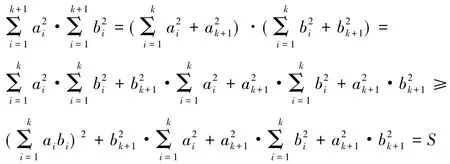
而

综上可得，当n=k+1时，结论亦成立.

2　数学分析的角度

2.1相关预备知识

定理2［3］(定积分的相关性质)设f(x)和g(x)在［a，b］上可积，有

注2:对于二重积分和三重积分，单调性和线性性仍然成立.

定理3［3］若矩形D=［a，b;c，d］，二元函数

2.2柯西不等式在数学分析中的形式及证明

形式Ⅲ设f(x)和g(x)在闭区间［a，b］上可积，则

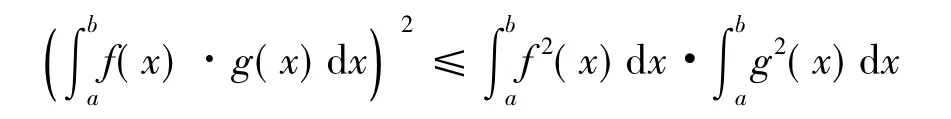
当且仅当f(x)=μg(x)(或g(x)=λf(x))时，等号成立.

当且仅当f(x)·g(y)=g(x)·f(y)，即f(x)=λg(x)(或g(x)=λf(x))时，等号成立.

3　高等代数的角度

3.1相关预备知识

定义2［4］设V是实数域R上的线性空间，在V上定义了一个二元实函数，称为内积，记作(α，β)，如果它具有以下性质:对α，β，γ∈V，k∈R，有

①(α，β)=(β，α);

②(kα，β)=k(α，β);

③(α+β，γ)=(α，γ)+(β，γ);

④(α，α)≥0，当且仅当α=0时等号成立.

这样的线性空间V称为欧几里得空间，简称欧氏空间.

定义3［4］非负实数称为向量α的长度，记为|α|.

3.2柯西不等式在高等代数中的形式及证明

证明若α=0，结论显然成立.若α≠0，作γ=tα+β，则由内积定义2的第④条，有(γ，γ)≥0，即(tα+β，tα+β)=(α，α)t2+2(α，β)t+(β，β)≥0.令f(t)=(α，α)t2+2(α，β)t+(β，β)，则f(t)是关于t且恒大于等于零的二次函数，所以Δ=(2(α，β))2－4(α，α)·(β，β)≤0，即(α，β)2≤(α，α)·(β，β)，两边开方，得|(α，β)|≤|α||β|.当α，β线性相关时，等号显然成立;反过来，当等号成立时，有Δ=0，所以二次函数f(t)有两个相同的根，即存在t使得f(t)=(γ，γ)=0，由第④条等式的成立条件可知，存在t使得γ=tα+β=0，即α，β线性相关.

综上，|(α，β)|≤|α||β|，当且仅当α，β线性相关时，等号成立.

4　三个角度下的柯西不等式之间的关系

4.1高等代数中的形式具有高度的概括性

事实上，不同形式下的柯西不等式均统一于欧氏空间两向量的内积运算之中.

在线性空间Rn中，对于向量α=(a1，a2，…，an)和β=(b1，b2，…，bn)可定义内积(α，β)=a1b1+a2b2+…+ anbn，则Rn就是一个欧氏空间.

注3:①不难发现，数量积是特殊的内积，故通常解析几何教材中，又将数量积称为内积.

②正是由于欧氏空间中柯西不等式的成立，才得以定义欧氏空间中两向量的夹角＜α，β＞=arccos，这为三维几何空间夹角的由来提供了理论基础.

在闭区间［a，b］上所有可积函数所构成的线性空间中，函数f(x)和g(x)可定义内积(f(x)，g(x))，则该线性空间就构成了一个欧氏空间.

综上，形式Ⅱ和形式Ⅲ可看做是形式Ⅳ的特殊形式.

4.2由解析几何角度下的推广形式证明数学分析中的形式

证明先引入引理A

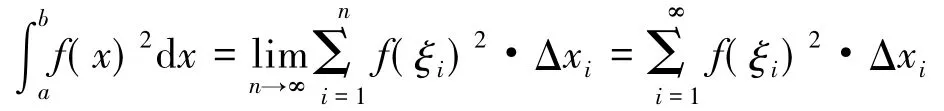
同理

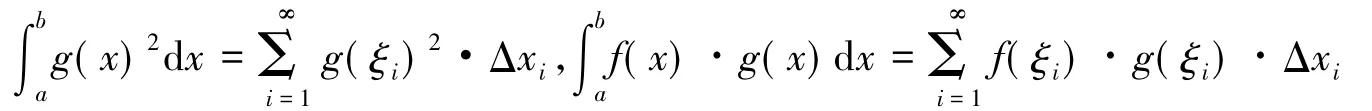
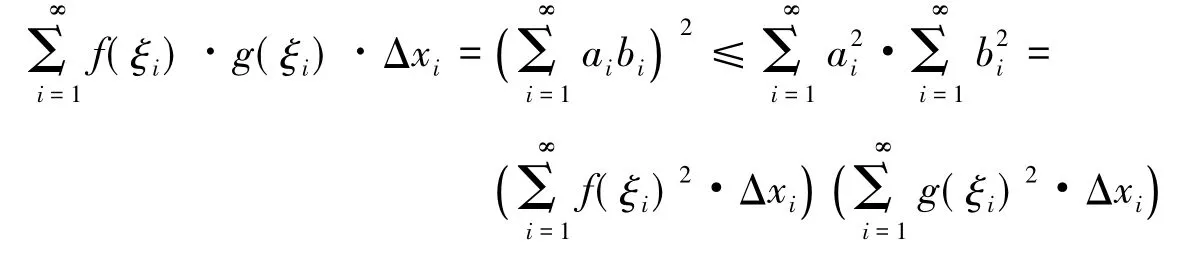
即

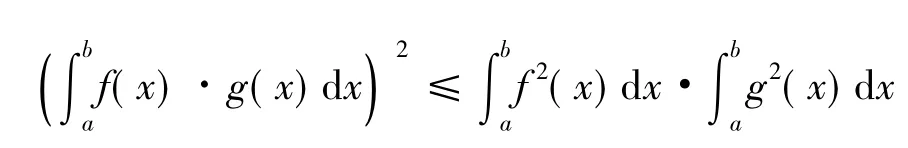
4.3用数学分析的知识证明解析几何角度下的推广形式

尽管形式Ⅱ是受形式Ⅰ的启发，对n利用数学归纳法所得到的解析几何角度下的推广形式，但该形式也可利用数学分析中的相关知识进行证明.

定理4［5］(凸函数的判别法)设f(x)在区间I上二阶可导，则f(x)在I上为凸函数的充要条件是f″(x)≥0.

定理5［5］(Jenson不等式)f(x)在I上为凸函数的充要条件是:对有如下不等式(1)成立:

下文将利用以上两个定理4，定理5，证明形式Ⅱ.

证明考察函数f(x)=x2，f″(x)=2＞0，由定理4知，f(x)=x2是R上的凸函数.

5　结语

在“三高”课程中，解析几何是借助坐标系用代数方法解决几何问题的学科;数学分析主要研究的是函数，研究函数的性质、微分和积分等内容，它往往通过函数模型来解决问题;而高等代数所讨论的是代数系统及其上的运算，如多项式环、线性空间等，它的特点是概念的高度抽象性和定理的高度概括性.一般而言，高等代数与解析几何的关系显得较为紧密，它们本质上是“数”与“形”的互动关系，高等代数中的理论可在解析几何中寻找模型，解析几何中的内容需依靠高等代数中的理论来支撑.

所举的柯西不等式在三个角度下的形式和证明以及它们的相互联系充分反映了数学思维的多样性与一致性，正所谓“殊途同归”.在“三高”课程的学习过程中，应经常反思三者的联系渗透之处，找出类似于柯西不等式这样的例子，并从三者不同的视角加以研究，以加深对例子本身以及“三高”课程的理解.

［1］咸伟志.从三个角度证明点到平面的距离公式［J］.重庆工商大学学报:自然科学版，2014，31(9):27-30

［2］吕林根.解析几何［M］.4版.北京:高等教育出版社，2006

［3］北京大学数学系几何与代数教研室前代数小组.高等代数［M］.3版.北京:高等教育出版社，2003

［4］欧阳光中.数学分析［M］.3版.北京:高等教育出版社，2007

［5］刘三阳.数学分析选讲［M］.北京:科学出版社，2007

Make a Thorough Inquiry for Cauchy Inequality in Three Views

XIAN W ei-zhi
(School of Mathematical Sciences，Chongqing Normal University，Chongqing 401331，China)

Cauchy inequality is one of themost significant inequalities in highermathematics.The inequality seeps in analytic geometry，mathematical analysis and higher algebra which are three main courses for the college studentsmajored in mathematics.This paper proves different forms of Cauchy inequality from the perspective of the three courses and explores the relations among them.Finally the papermakes a brief summary.

Cauchy inequality;scalar product;definite integral;Euclidean space;inner product

O122.3

A

1672－058X(2015)09－0033－06

10.16055/j.issn.1672－058X.2015.0009.009

2014－12－07;

2015－01－16.

重庆市重点实验室专项基金项目(CSTC2011KLORSE01).

咸伟志(1994-)，男，江苏南京人，从事数学与应用数学研究.