基于字典基函数框架的纤维方向分布模型重建

吴 烨 冯远静 李 斐 高成锋

(浙江工业大学信息工程学院, 杭州 310023)

基于字典基函数框架的纤维方向分布模型重建

吴 烨 冯远静*李 斐 高成锋

(浙江工业大学信息工程学院, 杭州 310023)

脑白质纤维方向分布模型重建是脑纤维成像的重要过程之一, 为纤维束跟踪提供精确的纤维方向估计。传统方法的约束条件往往依赖于先验的纤维方向信息, 限制了计算效率与精度的提高。提出一种基于字典基函数框架的纤维方向分布函数(fODF) 估计方法, 在单位球面上建立均匀的字典基函数分布, 构造基于字典基函数的球面反卷积模型，直接通过非负最小二乘方法求得基函数系数, 避免伪峰与复杂的算法以及更高阶的大规模病态逆问题的计算，使得纤维方向分布的稀疏性和非负性可以通过几个基函数的加权和很容易地表示。模拟磁共振数据与临床脑部数据的实验结果显示，该方法在同等条件下与目前流行的Super-CSD和QBI方法相比，计算复杂度大大降低, 计算时间仅为Super-CSD的1/3; 角度分辨率扩大到20°以内(其中, Super-CSD为40°, QBI为60°)。由于该方法简单高效, 角度误差不会随角度等参数的变化而跳变，也因为角度分辨率和角度误差性能的提升, 使得纤维方向的错误重构概率降低到8%以下，可为纤维跟踪技术提供精确的局部纤维走向。

字典基函数; 球面反卷积; 纤维方向分布; 方向分布模型

引言

人脑是世界上最复杂的系统之一,大约由1 000亿个神经元和100万亿条神经联络通路组成[1]。尽管相关的科学研究不断深化,但诸如阿尔兹海默症、帕金森综合症、孤独症、癫痫病、精神分裂症以及创伤性脑损伤等神经类疾病的根源仍然无法解释。2013年初,欧盟、美国等先后启动了脑研究计划,旨在从时间和空间上展示复杂的神经环路之间的相互作用和连通关系,脑科学的研究达到了一个前所未有的高度[2]。在大脑微结构成像中,扩散加权磁共振成像(diffusion weighted magnetic resonance imaging,DW-MRI)基于磁共振成像(magnetic resonance imaging,MRI)技术,是目前唯一有效的脑部结构无创检测技术。DW-MRI在常规MRI序列扫描的基础上,在Cartesian坐标系的3个正交方向施加两组巨大的对称梯度脉冲信号,用来反映水分子的扩散运动[3]。脑纤维成像技术以DW-MRI为基础,旨在准确地对大脑功能区的纤维束分布进行重构及成像分析。

目前,纤维跟踪技术是唯一的一种能在活体无创条件下获得脑纤维走向的方法,其基本思想是利用大脑体素内水分子扩散的各向异性对临床数据进行方向分布的建模,精确计算纤维在体素中的扩散方向,利用纤维跟踪算法对ROI内的纤维方向进行连接[4]。其中,扩散张量成像(diffusion tensor imaging,DTI)技术标定了脑白质水分子的扩散运动状态,是目前纤维重构中最常用的纤维方向估计模型[5-6],其基本思想是用一个二阶张量来描述纤维方向分布情况。正因为如此，DTI方法无法描述脑纤维存在的诸如交叉、分叉、扇形和瓶颈型等复杂结构。高角度分辨率成像(high angular resolution diffusion imaging,HARDI)技术的出现，成功地弥补了DTI成像的不足。现有的HARDI方法主要包括以扩散谱成像(diffusion spectrum imaging,DSI)[7],Q-ball成像(Q-ball imaging,QBI)[8]、高阶张量(high order tensor,HOT)[9-10]、球面反卷积(spherical deconvolution,SD)[11-12]为主导的多纤维重建方法。广义上讲,这些方法通过计算纤维方向分布函数 (fiber orientation distribution function,fODF) 建立扩散模型。其中,DSI方法将扩散函数(水分子的位移概率密度函数)表示为扩散信号在Q空间的傅里叶变换,通过扩散信号直接计算得到扩散函数，但是对采样的敏感程度和采样方向数要求较高,难以应用于实际临床中; Q-ball成像是一种相对于DSI来讲比较成熟的多纤维成像方法,通过测量扩散信号的FRT变换(funk radon transform,FRT)得到水分子的位移概率密度函数与零阶贝塞尔函数加权卷积后的径向积分[13],虽然成功地降低了采样时间,但对纤维方向的估计存在一定的随机性,这是因为QBI得到的扩散函数被一个零阶贝塞尔函数调整过,扩散函数极值频谱拓宽,纤维方向不明确,水分子的位移概率密度函数与纤维方向之间的关系并没有得到证实,所以得到的纤维方向并不一定与真实纤维方向一致; SD模型将扩散信号表示为纤维方向分布函数与单条纤维响应函数的卷积[11]，不需要任何的先验信息就能够准确地重构出脑白质纤维走向,但该模型直接从原始信号中通过反卷积得到,必然涉及高度病态性的高维逆问题计算,所以对噪声较为敏感; CSD技术[14]在原有的球面卷积方法中引入了迭代非负约束的优化过程,提高了角度纤维识别能力,抗噪性显著提高,但容易产生伪峰现象[15],且随着阶数的提高重建的稳定性大大降低,因此无法稳定重建小角度的纤维分叉。

近年来，随着信息技术进入大数据时代,磁共振数据也进入了高维高密度层次。虽然高精度的磁共振数据为精确重构复杂的脑纤维网络带来了可能,但同时也带来了数据分析上更大的挑战[16],纤维方向分布的群体建模过程变得相当复杂。传统的用提高阶数和复杂的数值优化算法来逼近纤维分叉角度的精确识别,显然无法满足临床应用的需要。笔者提出了一种基于字典基函数框架的纤维方向分布重建方法,建立了字典基函数的球面反卷积模型。用球面字典基的简单加权形式，避免了伪峰与复杂的算法,避免了更高阶的大规模病态逆问题的计算。在单位球空间上，建立基函数字典来搜索纤维方向的最优稀疏分布,以更小的计算量和更精确的角度分辨率为纤维跟踪技术提供纤维的精确走向。该方法分别在模拟磁共振数据与临床脑部数据中验证了可行性与高效性。

1 字典基函数框架的纤维方向分析

1.1球面反卷积模型

(1)

由于受数据采集噪声大等因素的影响,纤维方向分布带有一定的扩散性。纤维方向分布的计算依赖于大规模的病态逆问题。为了使重建的纤维方向分布更接近于真实的纤维方向,减少这种大规模的逆问题对重建的影响,笔者提出一种利用字典基函数框架来实现纤维方向分布的重建方法。

1.2方向基函数框架的纤维方向分析

单位时间内,水分子沿纤维方向的各向异性扩散呈现近纺锤体分布[19],通过基函数拟合离散fODF，可以直观地表示纤维方向的扩散分布特性。但是，纤维的线性走向对水分子扩散各向异性存在约束限制,使得真实纤维方向信息多数仅集中于fODF极值的邻域范围。2012年，在MICCAI会议中，Merlet等将该现象称为“纤维方向的稀疏性分布”[20]。目前,尽可能地提高有效纤维方向信息的比例,是构建高分辨率纤维方向分布的途径之一。

假设式(1)中所有非共线的纤维之间相对独立,那么可以将体素内的所有纤维主方向fri表示为

(2)

为了表示纤维在球面每个方向上的可能性分布,建立了一种预先定义的基函数字典(f1,f2,…,fm)近似模型(见图1)。那么，纤维方向分布模型可以表示为一组基函数字典(f1,f2,…,fm)的线性加权组合，即

(3)

式中,ω=[ω1,ω2,…,ωm]T是加权向量。

字典基函数是构成纤维方向的所有可能性分布的一组基。通过在球面上均匀采样m个离散点，可以得到均匀分布的单位向量υ，那么所建立的基函数字典均匀分布在整个Q空间上。

图1 一种字典基函数在单位球面空间的方向分布Fig.1 The orientation distribution of a dictionary basis funtion on a unit sphere

1.3字典基函数的建立

在数学分析中,正矢函数通过纬度来精确计算球面点距离,重新定义了余弦函数的球坐标形式,常用于航海中,尤其在小角度和短距离的计算上尤为适用。正矢函数可定义为

vercosin(θ)=1+cosωθ(θ∈[0,2π])

(4)

式中，ω∈+是周期参数,vercosin(θ)∈[0,2]在极坐标下是一个原点对称函数。

ϑ(γ,υ))

(α∈+,ϑ∈[0,π]

(5)

式中，ϑ(γi,υj)∈[0,π]是单位重建向量γi∈S2与单位基准向量υj∈S2的相对夹角α∈+是一个微调参数。

为了提高纤维方向分布的极值比例,使其具有更强的各向异性表现能力,拓展了函数的表示形式，有

Γμ(γ,υ)=Ζ·(1+αcos2ϑ(γ,υ))μ

(α,μ∈+ϑ∈[0,π])

(6)

式中，Ζ是归一化参数。

Γμ(γ,υ)中小于1的方向将通过幂运算而衰减,这提高了模型的径向紧凑程度,使得各重建点的fODF值比例更加鲜明(见图2)。

图2 正矢函数在球坐标下的分布。(a)μ=1；(b)μ=5；(c)μ=20Fig.2 The distribution of versine function on spherical coordinate. (a)μ=1；(b)μ=5；(c)μ=20

2 算法实现

2.1字典基函数框架的球面反卷积模型

在单位半球面上均匀采样m个重建向量υj。令γ←υ， 那么方向分布函数可以表示为

(7)

沿梯度方向,g的扩散衰减信号在方向υ上可以表示为

(8)

式中,系数ω是唯一的未知量,那么式(8)可以表示为线性方程,即

S=Aω+η

(9)

因为重建向量的采样数n远高于磁共振数据的梯度方向的采样数m，假定问题式(9)有无穷多解,然而所寻求的是在可行范围内符合纤维方向分布的最优解。此外,为了减小噪声η对重建的影响,可以将式(9)转化为能量方程来求解，即

(10)

2.2数学模型求解及特性分析

纤维沿扩散方向的稀疏分布和纤维方向的非负扩散是两大不可否认的物理性质。因此,有理由相信: 尽可能地平衡纤维方向的稀疏性与非负性的相对约束，是实现高角度分辨率纤维交叉的条件。在球坐标下，建立了纤维方向的字典空间,通过少量的加权系数来重建纤维方向的扩散模型(见图3)，避免求解时的强制稀疏约束。考虑到纤维方向的非负性约束,通过非负最小二乘法，得到与纤维主方向最接近的字典基函数，有为了提高fODF计算的精确性,通常会遍历整个球面进行球面向量的积分运算。但是，对连续球面充分采样是不可能的，且连续球面的积分过于复杂。笔者采用一种离散近似的方法,对单位正20面体进行∂次细分，获得(10×4∂+2)个重建向量(见图4)。细分次数越高，离散误差越小，但运算时间将延长。离散误差虽无法忽略，但通常限制在一定范围内的角度误差是允许的。例如，四次分形获得2 562个单位重建向量κi，令γ←κ,有

(11)

图3 模拟50°纤维分叉的fODF重构,在每个采样方向上的字典基函数所对应的加权系数ω的分布情况,由于研究的均匀采样是无序采样,因此横坐标仅表示每个采样方向对应于采样方向组中的位置。 (a)μ=50; (b)μ=100Fig.3 The weighted coefficients ω of corresponding basis function along each sampling direction for simulated 50° crossing fiber. Abscissa indicates the position of each sampling direction in the whole sampling group for the unordered uniform sampling. (a)μ=50; (b)μ=100

(12)

式中，ωi是式(11)的解。

通过灵活的基函数来提高纤维方向信息的比例,从而消除不必要的纤维存在,是一种间接但高效的方法,称之为字典稀疏性。利用字典基函数框架建立纤维方向分布模型,可以避免对复杂数值优化算法的需求,从而大幅降低计算时间。

图4 模拟50°纤维分叉重构。(a)2 562个均匀采样的重建方向中重构fODF的结果,白线为真实纤维方向; (b)重构的fODF的极值方向Fig.4 Simulate the reconstruction of fiber cross of 50°. (a) The fODF reconstruction from 2 562 uniform sampling directions,the white line is the real fiber direction; (b)The extremum direction of fODF

2.3实验方法

根据Söderman提出的方法[21]产生模拟加权磁共振信号，有

(13)

在模拟数据实验中,信号S通过以下方式添加Rician的随机噪声，即

(14)

式中，ζ1,ζ2～N(0,δ2)，δ=S0/SNR。在实验中,每次计算100次取平均结果。

临床数据实验利用3-T GE系统从51个梯度方向采集真实人脑数据,其中包括50个轴向切片,每个切片层的体素分辨率为256像素×256像素,b=2 000 s/mm2。在临床数据的实验中,主要关注的是重构的角度分辨率与重构的效率。

方法的实现主要分为6个步骤。

步骤1:在单位半球上均匀采样321个单位向量υ∈321×3；

步骤2:构建单位球上均匀分布的字典基函数；

步骤3:按本文2.1节和2.2节求解体素的基函数系数；

步骤4:4次分型单位正20边形,采样2 562个顶点向量κ∈2562×3；

步骤5:按本文2.2节计算纤维方向分布F∈2562；

步骤6:按每个fODF对应的向量κ进行拟合,得到每个体素的纤维方向分布模型。

2.4评价标准

本研究的目标之一是提高纤维方向的重建正确性，文献[22-23]中广泛使用了以下度量指标来评估纤维方向重建的效率与纤维方向的准确性。

1)错误纤维方向的概率: 量化一个体素内实际的纤维束数量M的先对重构准确度，有

(15)

为了真实反映算法的有效性，通常对同一模拟数据多次计算求平均值，或在某一真实区域内求得平均体素的Pd。

2)角度误差: 量化体素中重构的纤维方向角的精度，角度误差可计算为

(16)

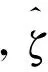
最终的值是每一个重构的纤维方向与标准方向对比后得到的误差平均值。其中，极值方向的检测是通过一个局部最大值搜索过程，仅考虑纤维方向附近在一个15°圆锥范围内的方向,因为这种评价标准对于小的交叉角度并不敏感，通常在30°～90°的范围内进行评价。另外，fODF值小于最大值得10%的识别为伪方向,要将其过滤。

3 结果

3.1模拟数据实验结果

纤维方向分布函数值可以看作是每一个重建方向上纤维方向分布的可能性,在真实纤维方向分布的主方向上fODF值最大。图5显示，当纤维交叉角度很小时，fODF的极值方向通过指数μ的提高将逐渐分离;当纤维交叉角度较大时，fODF的极值将通过μ的提高而逼近纤维的真实方向，这能够有效地减小角度误差。从图5(a)中可以看出,当交叉纤维无法重构时,fODF将集中于两个方向的中间,这在纤维跟踪时很容易被误判为单纤维,因此对基函数加幂将使得基函数更细致化,使得在加权重构时能够更精确地获得纤维方向分布模型。

图5 fODF在单位球面上的映射分布,彩色部分(从蓝色到红色)表示fODF的映射值(从0到1),白线表示纤维的真实方向。 (a)交叉角=15°,μ=10; (b) 交叉角=15°,μ=20; (c) 交叉角=15°,μ=50; (d) 交叉角=90°,μ=10; (e) 交叉角=90°,μ=20; (f) 交叉角=90°,μ=50Fig.5 fODF mapped on unit sphere,where the color part (from blue to red) indicates the mapping of fODF value (from 0 to 1),white line represents the real direction. (a)Cross=15°, μ=10; (b)Cross=15°, μ=20; (c)Cross=15°, μ=50.(d)Cross=90°, μ=10; (e)Cross=90°, μ=20; (f)Cross=90°, μ=50

准确重建fODF是纤维跟踪的前提,而估计的纤维方向通常因为误差和计算精度等因素难以达到理想的纤维方向分布,如图5红色中心的邻域周围,这样的误差在很小范围内是允许的。在图6中，分别对不同角度的纤维交叉重构,并计算了角度误差(见图7)。其中，Super-CSD[24]是Tournier[14]在CSD方法基础上不断优化而形成的一套比较完善的球面反卷积方法,是目前效果最好的方法之一,并广泛用于纤维跟踪技术中; QBI方法具有较高的计算效率和较低的重建误差,具有广泛的应用。

实验显示，DB-SD在角度分辨率上高于其他两种方法,对于35°以下的小角度纤维也能稳定地重建,更重要的是所有的角度误差均能够保持在6°以下。随着μ的提高，角度误差在很小的范围内产生波动,这是因为纤维信息比例的不断增加使得角度误差也愈加明显,但仍然能够保证在很小的角度误差范围内。图6 (d)显示，由于阶数的提高、待求解的未知系数增加，使得Super-CSD方法变得不稳定；对于DB-SD,由于字典基函数加权系数的稀疏性,只需要少量的未知系数就能够完整地重构,因此降低了因病态问题而引起的重构不稳定性。

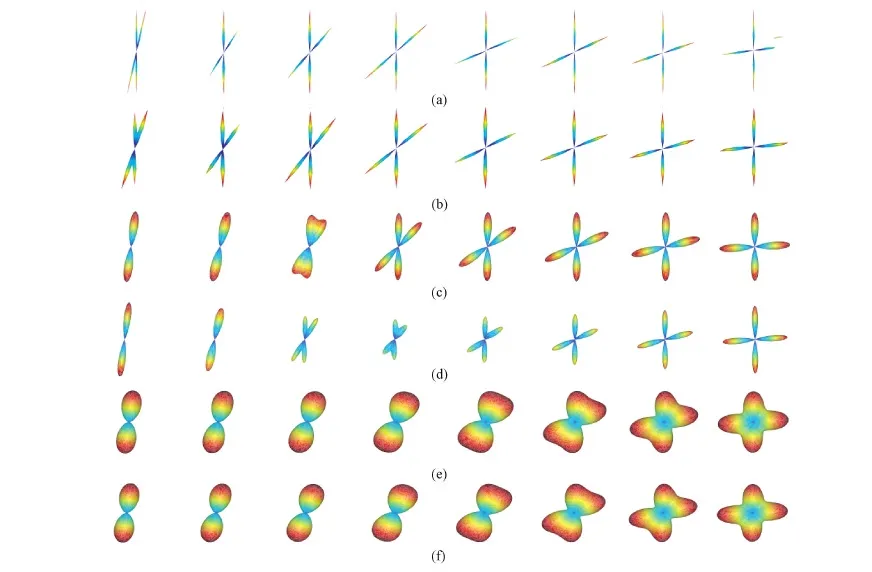
图6 模拟数据fODF的重建结果,其中SNR=40,从左到右依次表示模拟纤维交叉角度从15°～85°(间隔10°)。(a)DB-SD μ=20; (b)DB-SD μ=50; (c)Super-CSD 阶数=12; (d) Super-CSD阶数=16; (e)QBI阶数=12; (f) QBI 阶数=16Fig.6 The reconstruction results of fODF of simulated data, where SNR=40, from left to right were represented the fiber cross angle from 15 degree to 85 degree(interval 10 degree). (a)DB-SD μ=20; (b)DB-SD μ=50; (c)Super-CSD order=12; (d) Super-CSD order=16; (e)QBI order=12; (f)QBI order=16

图7 模拟数据纤维方向分布重建结果的角度误差(其中SNR=40)Fig.7 The angular error of the fiber orientation distribution reconstruction from simulated data. SNR=40

图8是一组不同信噪比下的纤维方向错误重构概率的对比实验，其中Super-CSD和Qball方法的阶数设置为14阶; 实验中的DB-SD方法设置μ=20。实验分别对同一角度测试100次，累计这100次的重构结果取平均值测试。实验显示,本方法具有稳定高效的纤维方向重构效果,这是因为DB-SD方法在提高角度分辨率的同时并未增加系数计算的复杂度,可以大大提高重建的稳定性,在不同SNR下均能保持较高的重建效率。图9是一组不同敏感系数和不同噪声共同影响下的各角度重建误差的实验。实验显示，当敏感系数较低时(见图9中的(a)和(b)),信号本身重构的难度增加,使得Q-ball方法的角度误差普遍较大,这种情况下纤维的重建效果均不佳,纤维重建的结果并不可信; Super-CSD方法在纤维交叉角度低于45°时角度误差较大,随着角度的增加反映出了误差逐渐下降,随着误差的增加也反映出了Super-CSD具有一定的抗噪性,但在100次的同等条件重建下,稳定性仍然较低; DB-SD方法虽然在图9(a)的35°时反映出了角度误差约为10°,但总体角度误差均较低,随着噪声等级的变化,依然能够保证稳定性与较低的角度误差。当敏感系数较高时(见图9中(c)和(d)),Q-ball方法在交叉角度较大时重建的稳定性较好; Super-CSD方法虽然在角度误差上与DB-SD方法相当,但稳定性却弱于本方法。事实上,敏感稀疏与噪声是临床数据应用时重要的影响参数之一,既要保证不同参数下重建的相对稳定，更要保证误差较低。

图8 模拟数据下不同信噪比的纤维方向的错误重构概率。(a) SNR=10; (b) SNR=40Fig.8 The probability of false fiber detection of simulated reconstruction with different SNR. (a) SNR=10; (b) SNR=40

图9 模拟数据下不同信噪比与敏感系数影响的纤维方向分布重建结果的角度误差的均值和标准差。(a) b=1 000 s/mm2, SNR=10; (b) b=1 000 s/mm2, SNR=40; (c) b=3 000 s/mm2, SNR=10; (d) b=3 000 s/mm2, SNR=40Fig.9 The mean and standard deviation of the angular error in orientation reconstruction with different SNR and sensitivity coefficient from simulated data. (a) b=1 000 s/mm2, SNR=10; (b) b=1 000 s/mm2, SNR=40; (c) b=3 000 s/mm2, SNR=10; (d) b=3 000 s/mm2, SNR=40

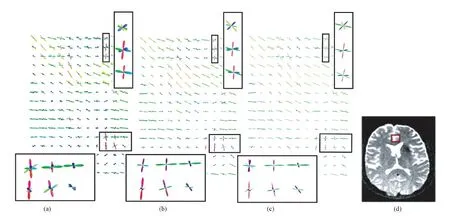
图10 扣带与扣带回皮质相交区域的纤维方向重建实验对比,其中颜色表示纤维主方向在RGB规则上的映射。 (a)Super-CSD方法,球谐阶数=12; (b)DB-SD方法,μ=20; (c)DB-SD方法,μ=50; (d)人脑冠状面切片的DW-MRI图,灰度颜色映射为FA值的大小,其中白色表示各向异性较大的区域Fig.10 The reconstruction of the intersection redion of cigulum and cingulate cortex with different methods,where the color representation mapping fiber main direction in RGB rules. (a)Super-CSD method,where SH order=12; (b)DB-SD method, where μ=20; (c)DB-SD method, where μ=50; (d) the human brain coronal sections in the lower left corner, gray value indicates the size of FA values, and white part said the area where a large anisotropy

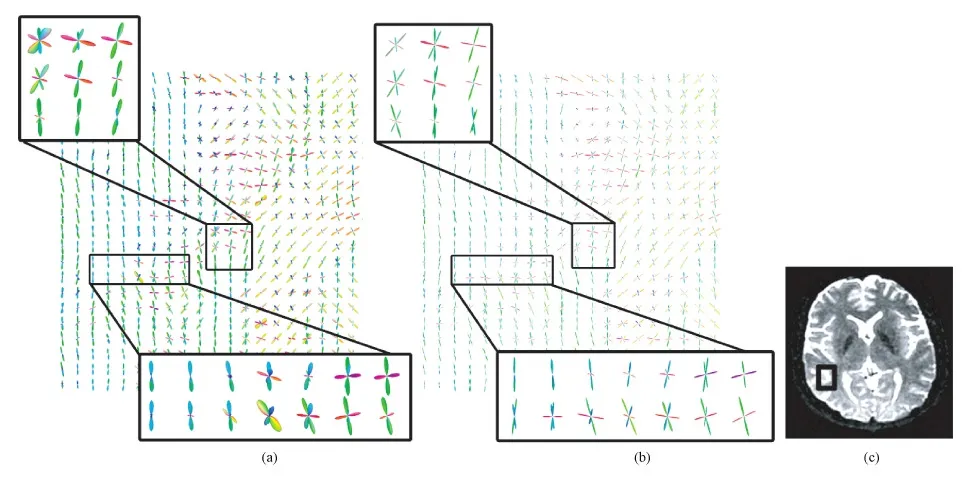
图11 下胼胝体与下扣带相交区域的纤维方向重建实验对比,其中颜色表示纤维主方向在RGB规则上的映射。 (a)Super-CSD方法,球谐阶数=12; (b)DB-SD方法,μ=20; (c)人脑冠状面切片的DW-MRI图,灰度颜色映射为FA值的大小,其中白色表示各向异性较大的区域Fig.11 The comparison of fiber direction reconstruction in the intersection region of the corpus callosun and cingulun,where the color representation mapping fiber main direction in RGB rules, ROI schematic representation the human brain coronal sections, gray value indicates the size of FA values. (a)Super-CSD method, where SH order=12 (b)DB-SD method, where μ=20;(c) The human brain coronal sections in the lower left corner, gray value indicates the size of FA values, and white part said the area where a large anisotropy

从本质上来看，Super-CSD使用复杂的球谐函数作为基函数,利用Tikhonov正则化方法来诱导负方向的消除。从计算效率来看,笔者使用简单的球面正矢函数作为基函数,并未使用复杂的数值逼近算法。Super-CSD的角度分辨率的提高依赖于阶数的增加,但从实验中可以看出,Super-CSD方法在高阶非常不稳定; 而QBI方法的角度分辨率较低,无法很好地重构60°以下的纤维交叉,随着阶数的增加,也并未改善其重建精度。因此，从角度分辨率和计算效率来说，本方法都优于目前常用的Super-CSD方法和QBI方法,具有很好的临床应用前景。

3.2临床数据实验结果

由于QBI方法的角度分辨率低等原因，实际数据仅与重建效果较好的Super-CSD方法对比。给出了DB-SD方法与Super-CSD方法在分数各向异性(fractional anisotropy,FA)背景下的纤维束交叉区域矢状切面的纤维方向重建实验结果。其中,图10的ROI区域为上扣带与扣带回皮质的相交区域附近,图11的ROI区域为下胼胝体与下扣带的相交区域附近。

由图10中扣带与扣带回皮质相交区域的多纤维交叉可见,不同方向的多纤维经过区域,DB-SD方法都能够很好地识别，尤其在绿色部分,纤维的方向保持一致,更符合纤维的真实分布；在图11中，横向扣带穿过胼胝体纤维,DB-SD方法很好地还原了这一事实,并且在下胼胝体与下扣带相交区域,DB-SD方法表现出了高角度分辨率的优势。另外,随着基函数的幂μ提高,重构的角度误差降低，角度分辨率提高,然而增加的计算量是否会提高重构的时间,笔者做了一组对比实验。其中，∂是采样重建向量的分形次数(见表1)。实验分别对其中一层的256体素×256体素进行实验,计算单个体素重构的平均时间(ms)。从表格可以看出,μ的提高对算法本身的重构时间并未造成太大的影响,这是由于每个体素使用同样的字典基函数分布,不同的是基函数所对应的加权系数,因此在对体素地群体重构时,并不需要反复计算每个体素的基函数分布,而只需一次计算。另外,由于基函数的加权稀疏的稀疏性,使得DB-SD方法通过几个简单的基函数加权叠加就可以获得很好的纤维方向分布。更值得一提的是，传统方式提高阶数增加了未知系数的维度，使得重构的复杂度大大增加,而DB-SD方法的系数维度仅与球面基函数分布的个数相关。这样,DB-SD相比其他方法可以大大地降低计算的复杂度,因此减少了重构时间。那么,应用时可以在保证稳定的前提下，适当地提高μ来重构高角度分辨率的纤维。

表1每个体素中纤维方向重建的平均时间

Tab.1Themeantimeneededforfiberdirectionreconstructioninsinglevoxelwithdifferentmethod

分型次数平均重建时间/sDB-SDSuper-CSDμ=10μ=50μ=100阶数=12∂=313.513.413.635.7∂=413.714.014.036.8∂=515.615.915.943.5

4 讨论和结论

近年来,随着脑研究计划在全球范围内的开展,大脑成像技术取得了巨大进步。对于大脑微结构和纤维群体成像而言,纤维跟踪技术将临床医学与信息技术结合,旨在揭示复杂脑网络的微结构信息。随着信息技术的大数据时代到来,给体素建模和数据分析带来了更大的挑战。纤维方向分布模型重建的精度与效率的平衡，是整个脑纤维成像的难点之一。针对这一问题,本研究设计了一种字典基函数框架下的纤维方向分布模型重建算法,在单位球下构建基函数分布框架,实现了对不同的纤维方向分布，仅需少量的加权系数就可以快速重建。实验结果显示,DB-SD方法确实能够在角度分辨率和计算效率中展示出优势。目前,纤维方向分布模型重建有3种思路: 一种是通过Q空间的信号变换，还原纤维方向分布模型,如Q-ball; 另一种是通过球面反卷积方法,从信号中还原fODF,如CSD; 还有一种则是多峰函数拟合的方式。本研究的基本思路介于后两种思路之间。首先,本研究采用了一种简单的双叶函数，建立单位球上的字典基函数分布; 其次,本研究使用球面反卷积模型，计算字典基函数的加权系数,通过简单的非负最小二乘方式，就可以获得稀疏的字典基函数表示的纤维方向分布模型。从图1的三维字典基函数分布可以看出,均匀的球面采样所构造出的字典基函数分布是均等的。为了突出纤维的主方向信息,本研究通过加幂的方式集中纤维方向(见图5)，随着幂的增加,fODF在单位球面上的映射分布更加集中于纤维的真实方向。虽然幂的增加带来了一定的计算量,但DB-SD方法的加权系数是稀疏的(见图3),这在计算中大大降低了基函数拟合的复杂度。本研究的一个特点是：利用简单而高效的方式，获得高角度分辨率、低重构误差的纤维方向分布模型。从图6中可以看出,DB-SD方法具有很好的稳定性,并且对于小角度的纤维分布能够很好地重构。衡量纤维重构算法的重要指标之一是角度误差,从图7～9中可以看出,由于100次重构中纤维角度产生了不同程度的变化,因此平均角度误差也反映出DB-SD方法相比其他两种方法具有更好的稳定性。相比模拟数据的实验环境,实际数据具有更多的不确定因素和复杂性,如图10、11所示。由于每个体素是独立建模,在不考虑先验条件下,实际数据的高角度分辨率很难保证。但在实验中,DB-SD方法相对于Super-CSD方法,大大地提高了角度分辨率,更加适应整体的纤维束走向。

同时,本实验结果也表明:一方面,多峰函数拟合往往过于复杂，并且很难保证效率和稳定性; 另一方面,纤维束本身具有一定的走向性约束,无论使用任何重构方法都应该符合整体的纤维束走向。但在图10中,DB-SD方法在单条纤维束中也可能产生多纤维,这是由于实际数据中纤维往往具有不可预测的分支。

本研究提出了一种基于字典基函数框架的fODF估计方法,建立了字典基函数的球面反卷积模型。用球面字典基的简单加权形式，避免了伪峰与复杂的算法,避免了更高阶的大规模病态逆问题的计算。纤维方向分布的稀疏性和非负性可以通过少量的基函数的加权来得到,实验测试表明，笔者提出的DB-SD方法更加逼近纤维的真实方向,角度分辨率大幅提高,以小范围的角度误差稳定识别出小角度的纤维分叉。DB-SD方法在计算时间、角度分辨率和角度误差等方面都优于现有效果较好的Super-CSD方法和QBI方法。将进一步促进纤维跟踪技术在临床中应用。

[1] 梁夏, 王金辉, 贺永. 人脑连接组研究: 脑结构网络和脑功能网络[J]. 科学通报, 2010 (16): 1565-1583.

[2] 朱丽君, 朱元贵, 曹河圻, 等. 全球脑研究计划与展望[J]. 中国科学基金, 2013,27(6): 359-362.

[3] Mori S, Crain BJ, Chacko VP,etal. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging[J]. Anuals of Neurology, 1999,45(2): 265-269.

[4] Mori S, van Zijl P. Fiber tracking: principles and strategies-a technical review[J]. NMR in Biomedicine, 2002,15(7-8): 468-480.

[5] Assaf Y, Pasternak O. Diffusion tensor imaging (DTI)-based white matter mapping in brain research: a review[J]. Journal of Molecular Neuroscience, 2008,34(1): 51-61.

[6] Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging[J]. Biophysical journal, 1994,66(1): 259-267.

[7] Wedeen VJ, Wang RP, Schmahmann JD,etal. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers[J].Neuroimage, 2008,41(4): 1267-1277.

[8] Cheng J, Ghosh A, Deriche R,etal. Model-free, regularized, fast, and robust analytical orientation distribution function estimation[C]//Proceedings of the 13th international conference on Medical image computing and computer-assisted intervention: Part I. Berlin: Springer-Verlag, 2010: 648-656.

[9] 李蓉, 冯远静, 邵开来, 等. 磁共振扩散高阶张量成像的脑白质纤维微结构模型及特征提取算法[J]. 中国生物医学工程学报, 2012,31(3): 365-373.

[10] Hlawitschka M, Scheuermann G. Tracking lines in higher order tensor fields[J]. Scientific Visualization: Advanced Concepts, 2010, 1: 124-135.

[11] Kaden E, Knösche TR, Anwander A. Parametric spherical deconvo lution: Inferring anatomical connectivity using diffusion MR imaging[J]. NeuroImage, 2007,37(2): 474-488.

[12] Jeurissen B, Leemans A, Tournier JD,etal. Estimating the number of fiber orientations in diffusion MRI voxels: a constrained spherical deconvolution study[C]//International Society Magnetic Resonance in Medicine. Stockholm: Wiley Online Library, 2010: 573.

[13] Tuch DS. Q-ball imaging[J]. Magnetic Resonance in Medicine, 2004,52(6): 1358-1372.

[14] Tournier J, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution[J]. NeuroImage, 2007,35(4): 1459-1472.

[15] Parker GD, Marshall D, Rosin PL,etal. A pitfall in the reconstruct tion of fibre ODFs using spherical deconvolution of diffusion MRI data[J]. Neuroimage, 2013,65: 433-448.

[16] 张艳, 宋志坚. 脑白质纤维束跟踪算法的研究进展[J]. 复旦学报(医学版), 2014,41(1): 1-7.

[17] 吴占雄, 朱善安. 基于移动最小二乘法的白质纤维束走向跟踪[J]. 浙江大学学报(工学版), 2011,45(3): 458-461.

[18] Tournier J, Calamante F, Gadian DG,etal. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution[J]. NeuroImage, 2004,23(3): 1176-1185.

[19] Frank LR. Characterization of anisotropy in high angular resolution diffusion-weighted MRI[J]. Magnetic Resonance in Medicine, 2002,47(6): 1083-1099.

[20] Merlet S, Caruyer E, Deriche R. Parametric dictionary learning for modeling EAP and ODF in diffusion MRI[C]//Medical Image Computing and Computer Assisted Intervention (MICCAI).Beilin: Springer, 2012, 7512: 8 p.

[21] Söderman O, Jönsson B. Restricted diffusion in cylindrical geome try[J]. Journal of Magnetic Resonance, Series A, 1995,117(1): 94-97.

[22] Landman BA, Bogovic JA, Wan H,etal. Resolution of crossing fibers with constrained compressed sensing using diffusion tensor MRI[J]. NeuroImage, 2012,59(3): 2175-2186.

[23] Michailovich O, Rathi Y, Dolui S. Spatially regularized compressed sensing for high angular resolution diffusion imaging[J]. IEEE Transactions on Medical Imaging, 2011,30(5): 1100-1115.

[24] Calamante F, Tournier JD, Jackson GD,etal. Track-density imaging (TDI): super-resolution white matter imaging using whole-brain track-density mapping[J]. Neuroimage, 2010,53(4): 1233-1243.

A Novel Fiber Orientation Distribution Reconstruction Method Based on Dictionary Basis Function Framework

Wu Ye Feng Yuanjing*Li Fei Gao Chengfeng

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Brain WM fiber orientation reconstruction is the throat of fiber imaging that set the premise of fiber tractgraphy. In conventional approaches, constraint conditions are dependent on prior information of fiber orientation, limiting the improvement of computation efficiency and precision. In this work, we presented a dictionary basic function based fiber orientation distribution function (fODF) estimation method. First, the uniform distribution of dictionary basis functions on unit sphere was established; second, spherical deconvolution (SD) model based on the dictionary basis functions was established; third, the coefficients of basic functions were directly obtained using non-negative least square method. The proposed method successfully avoided the spurious peak, leases computation burden and eliminates higher order ill-posed inverse problem, which makes the sparsity and non-negativity needed for the representation straightforwardly represented by weighted sums of basic functions. Experiments on simulated and clinical brain data both verified that computational complexity of the proposed method is much less than that of Super-CSD and QBI under the same conditions, such as, computational time of the method is a third as long as that of Super-CSD; the angular resolution of the method increases to a range of 20°, while Super-CSD is 40° and QBI is 60°. Because the method is simple and efficient, angular error does not change with such parameters as angle, and with the addition of the improvement of angular resolution and angular error performance, the probability of error fiber orientation reconstruction decreases to less than 8%, which will provide accurate local fiber orientation for fiber tractgraphy.

dictionary basis function; spherical deconvolution; fiber orientation distribution; orientation distribution model

10.3969/j.issn.0258-8021. 2015. 03.006

2014-07-02， 录用日期:2015-04-07

国家自然科学基金(61379020); 浙江省自然科学基金(LY13F030007)

TP391

A

0258-8021(2015) 03-0297-011

# 中国生物医学工程学会会员(Member, Chinese Society of Biomedical Engineering)

*通信作者(Corresponding author)， E-mail: fyjing@zjut.edu.cn