XFEM在高压管道裂纹扩展计算中的应用

摘要： 介绍XFEM的基本理论，针对常规有限元计算困难的三维裂纹，运用XFEM完成三维高压管道中的裂纹扩展计算.根据管道裂纹扩展的计算结果，总结得到管道裂纹扩展的规律，得到径向裂纹比轴向裂纹更严重的结论.

关键词： 高压管道； 疲劳； 裂纹扩展； 三维裂纹； 有限元

中图分类号： U4文献标志码： B

Abstract： The basic theory of XFEM is introduced. As to the problem that it is difficult to calculate 3D crack by the normal finite element， XFEM is used to perform the crack propagation calculation on a 3D highpressure pipe. According to the crack propagation calculation results of the pipe， the law of pipe crack propagation is summarized and it is concluded that the crack in radial direction is more critical than that in axial direction.

Key words： highpressure pipe； fatigue； crack propagation； 3D crack； finite element

收稿日期： 2014[KG*9〗05[KG*9〗10修回日期： 2014[KG*9〗10[KG*9〗24

作者简介： 陈星文（1983—），男，山东青岛人，工程师，硕士，研究方向为管道力学，（Email）chxw@snerdi.com.cn0引言

在用有限元法处理工程问题时，由于常规有限元法的位移函数是连续函数，所以利用常规有限元法所建立的单元其内部位移必须是连续的.因此，常规有限元法在处理如裂纹这类不连续问题时，必须把裂纹面作为单元边界面，裂纹尖端作为为单元的节点.

在裂纹尖端附近区域，应力集中使其应力急剧变化.常规有限元法的位移函数是多项式，在裂纹尖端的网格划分中，若多项式的次数不变，要模拟裂纹尖端附近应力的急剧变化，使有限元解逼近于精确解，则必须将单元尺寸划分得非常小.另外，如果单元尺寸不变，可通过增加多项式的次数来反映裂纹尖端单元的应力变化.实践证明，在处理裂纹尖端应力集中这类问题时，高次多项式的逼近性能非常差，求解结果不能满足精度要求.[1]

在模拟裂纹扩展问题上，常规有限元显得更加无能为力，由于必须把裂纹面设置为单元界面，裂纹尖端设置成单元节点[12]，因此当裂纹扩展后，就必须对结构重新划分网格，而由于裂纹尖端存在应力集中，网格必须细化，所以会极大地增加计算量，对于一些复杂结构问题甚至无法实现.

由于常规有限元法在计算裂纹问题上存在上述缺陷，1996年德克萨斯大学教授MELENK等[3]提出单位分解概念，通过单位分解，扩大有限元形函数的形式，使得不连续函数和非多项式函数可以添加到有限元的位移函数中，使得许多在相关问题上逼近性很强的函数可以用于有限元单元位移函数，从而使有限元的计算变得简洁，结果更加精确.1999年，以BELYTSCHKO为首的美国西北大学力学研究组提出XFEM理论：在单位分解法的基础上改变常规有限元的位移函数.[45]其在常规有限元位移函数的基础上加上裂纹尖端位移函数因子，[68]从而无须将网格在裂纹尖端细化就可以准确地逼近结构的精确解.而且，XFEM不需要将结构内部存在的几何或物理界面作为网格划分的边界[9]，其所使用的网格可以与结构内部的形状特点无关.这样，在裂纹扩展的过程中就不需要对结构重新进行网格划分，为裂纹扩展计算提供可行性和便捷性.

1XFEM基本理论

1.1裂纹界面位移改进函数

在常规有限元中，单元位移函数通常表示为u=Niui

v=Nivi

w=Niwi（1）式中：ui，vi和wi为节点i的位移；Ni为结构的形函数.

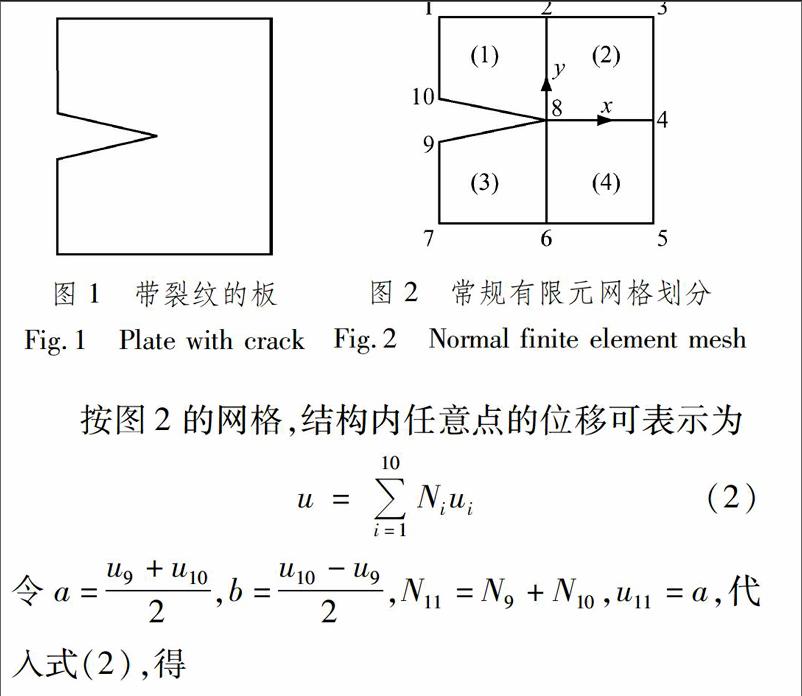
由于常规有限元的单元位移函数是连续函数，因此对结构进行网格划分时裂纹面必须作为单元的边界，以保证有限元单元内部位移的连续性.对于带裂纹的平板（图1），按常规有限元方法，在不考虑裂纹尖端应力集中的情况下，网格划分见图2.

按图2的网格，结构内任意点的位移可表示为u=10i=1Niui（2）令a=u9+u102，b=u10-u92，N11=N9+N10，u11=a，代入式（2），得u=8i=1Niui+N11u11+bN11H（x）（3）式中：H（x）称为跳跃函数，H（x）=1，y>0

-1，y<0 .

式（3）右端前2项即为常规有限元的位移函数，最后一项跳跃函数则代表单元内不连续区域的存在.式（3）说明图2所示的单元形函数可由图3所示的有限元单元形函数和一个代表裂纹的单元内不连续函数组成.这样，在求解含裂纹的结构时，只需改进包含裂纹的单元的位移函数，即在单元位移函数上添加跳跃函数bN11H（x），就无须再将裂纹面设置为单元的边界面，却依然可以得到足够精确的解.[3]

1.2裂纹尖端位移函数

处理裂纹尖端应力集中问题时，根据单位分解法[3]，可以将裂纹尖端所在单元的节点自由度加强，即在常规有限元位移函数上加上已知的裂纹尖端渐近位移函数，从而能够在不细化网格的前提下，仍然能在裂纹尖端单元内得到精确、连续、光滑的解.

裂纹尖端渐近位移函数为u=Mm=1αmψm（4）式中：αm为渐近函数权重值；ψm为裂纹尖端位移函数；M为裂纹尖端位移函数所包含的函数总个数.[5]

裂纹尖端位移函数ψm为已知的渐近位移函数场，能够精确反应裂纹尖端附近区域的位移场.文献[6]给出各向同性弹性体的裂纹尖端渐近位移函数为

式中：θ和r是以裂纹尖端为原点的极坐标的2个坐标参数，θ=0的方向平行于裂纹面.对于各向同性弹性体材料，无论其承受何种载荷，其裂纹尖端的位移场均可用式（5）的4个函数表示.对于各向异性弹塑性材料或复合材料，裂纹尖端位移改进函数还需进一步研究.

1.3最终的单元位移函数

对于存在任意裂纹的结构体，裂纹界面位移函数和裂纹尖端位移函数都必须添加到结构的单元位移函数中，才能正确模拟结构的裂纹.综合式（2）和（3）可得含任意裂纹结构的改进位移函数为

式中：I为结构整个区域上的节点；J为裂纹经过单元但不包括裂纹尖端单元上的节点；k1和k2为裂纹尖端单元上的节点.裂纹尖端单元内的节点不需要添加裂纹界面位移函数，因为裂纹尖端位移函数给出的是裂纹尖端所在单元区域精确的位移场，所以不需要再模拟裂纹界面的存在.含任意裂纹平面板上需加强的节点示意图见图4，图中圆圈标注的节点为需要增添裂纹界面位移函数的节点，四边形标注的节点为需要增添裂纹尖端位移函数的节点.

2计算实例

通过一个简单的实例证明XFEM在裂纹扩展计算上的准确性.一个1 m×1 m各向同性的薄板见图5.薄板中包含一个水平裂纹，一端垂向简支，一端施加均匀拉力；另外，为防止结构在变形中存在水平转动，在薄板的水平方向施加旋转约束.薄板均匀拉力为σ=2.0×109 Pa，弹性模量为E=2.1×1011 Pa，泊松比为0.3，板中初始裂纹长度为0.3 m.

2.1XFEM求解裂纹的扩展

利用XFEM求解裂纹的扩展，其网格划分可以不考虑其内部裂纹面，只需将裂纹附近的单元位移函数按XFEM改进即可，薄板的网格划分见图6.

薄板裂纹破坏准则采用最大主应力准则[7]，假定当板中第一主应力达到84.4 MPa（此数据可任意假定，不影响裂纹的扩展路径）时，裂纹开始扩展，计算得到薄板裂纹扩展的路径见图7.

2.2用应力强度因子K1和K2求解裂纹的扩展

用一个简单但繁琐的方法证明XFEM在裂纹扩展计算上的准确性.针对第2.1节中的薄板，采用常规有限元法模拟薄板中裂纹的存在，细化裂纹尖端网格，可以得到裂纹尖端的应力强度因子.[10]根据文献[8]，对于均匀的各项同性线弹性材料，可以用应力强度因子求出板中裂纹的扩展方向θ=cos-13K22+K41+8K21K22K21+9K22（7）式中：θ是从裂纹初始认定扩展方向q逆时针转向裂纹法线的度数.裂纹初始认定扩展方向为与裂纹尖端处裂纹面平行且远离裂纹的方向.

对此例中1 m×1 m的薄板采用线性扩展方法，使裂纹沿θ方向扩展5 cm的长度，然后再对此时的薄板重新划分网格，细化裂纹尖端，再求出此时薄板的裂纹扩展方向，以此反复可求出薄板裂纹最终的扩展路径.

经16步迭代，最终求出薄板裂纹的扩展路径.其中第2步和第8步的薄板网格划分见图8和9.比较图8与图6的网格划分，可知XFEM在处理含裂纹结构问题上的简洁性.

a）路径b）网格最终得到的薄板裂纹扩展路径见图10.比较图10与图7，可以看出裂纹扩展路径基本一致.

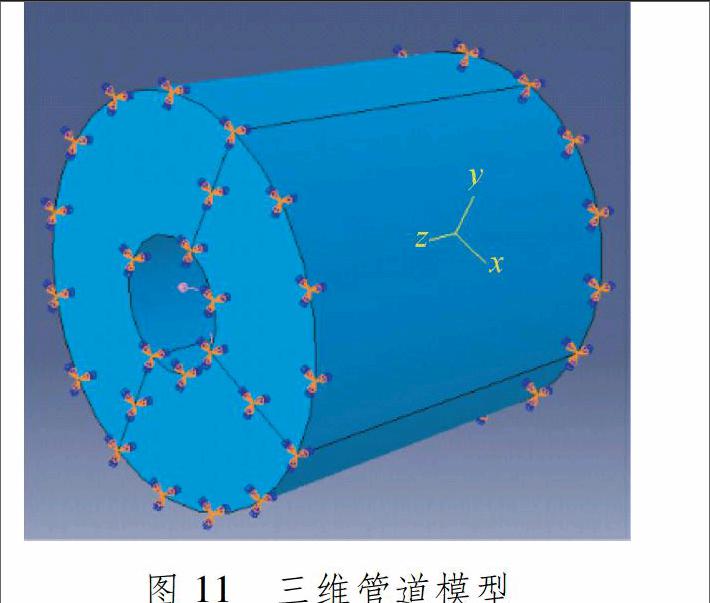
3XFEM在管道裂纹扩展计算中的应用将XFEM应用到三维高压管道模型计算中.为更好地观察裂纹扩展，采用较大壁厚的管道.设管道的外径为60 mm，内径为20 mm，长度为90 mm，其弹性模量为E=2.1×1011 Pa，泊松比为0.3.管道包含任一裂纹，管道内表面受径向均匀压力.管道两端边界条件为固支.破坏准则采用最大主应力准则，当最大主应力达到84.4 MPa时，裂纹开始扩展.其三维模型见图11.

针对上述管道模型，内表面任意初始轴向表面裂纹的管道裂纹扩展结果见图12，外表面任意初始轴向表面裂纹的裂纹扩展结果见图13，内部有1个初始环向深埋裂纹的裂纹扩展结果见图14.

对于内表面受均匀径向压力的管道，通过对包含各种不同裂纹面的管道的断裂计算，根据其裂纹扩展路径，得到以下规律.

1）裂纹初始扩展总是从裂纹面沿管道径向向管道内表面扩展，在裂纹穿透内表面后，再沿轴向和径向向外表面方向同时扩展，最终穿透外壁.

2）根据裂纹的扩展路径和管道的受力分析，同等长度的径向裂纹比轴向裂纹对管道的承载能力影响更大，这也符合内表面均匀受压管道的受力特性.因为相对于拉力平行于裂纹长度方向，拉力垂直于裂纹长度方向时裂纹面更容易发生断裂扩展破坏.

4结论

1）对于裂纹疲劳扩展问题，由于采用XFEM，结构在裂纹扩展后不需要重新划分网格.因此，XFEM在模拟裂纹的疲劳扩展问题上具有很大的优势，特别是当结构模型非常复杂时，其优势更明显.

2）给出各向同性线弹性材料的裂纹尖端位移改进函数，而对于非各向同性、非线性的材料或者复合材料，其裂纹尖端位移改进函数仍需要进一步的研究，以使XFEM可以应用到更多的领域.

3）由于XFEM可提高有限元在处理不连续问题上的准确性和便捷性，所以其在复杂流体、复杂传热、相变和流固耦合等复杂不连续和多项介质耦合中的应用可以进行更多研究.参考文献：

[1]朱伯芳. 有限单元法原理与应用[M]. 2版. 北京： 中国水利水电出版社， 1998： 11.

[2]丁隧栋. 断裂力学[M]. 8版. 北京： 机械工业出版社， 1997： 21.

[3]MELENK J M， BUBSKA I.The partition of the unity finite element method：basic theory and applications[J]. Comput Methods Appl Mech & Eng， 1996， 139（14）： 289314.

[4]MOES N， DOLBOW J， BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. Int J Numer Methods Eng， 1999， 46： 131150.

[5]BELYTSCHKO T， BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. INT J Numer Methods Eng， 1999， 45（5）： 601620.

[6]FLEMING M， CHU Y A， MORAN B， et al.Enriched elementfree Galerkin methods for crack tip fields[J]. Int J Numer Methods Eng， 1997， 40： 14831504.

[7]MAITI S K， SMITH R A. Comparison of the criteria for mixed mode brittle fracture based on the preinstability stressstrain field， part I： slit and elliptical cracks under uniaxial tensile loading[J]. Int J Fracture， 1983， 23（4）： 281295.

[8]ERDOGAN F， SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. J Basic Eng， 1963， 85（4）： 519527.

[9]李录贤， 王铁军. 扩展有限元法（XFEM）及其应用[J]. 力学进展， 2005， 35（1）： 520.

LI Luxian， WANG Tiejun. Extended finite element method and its applications[J]. Adv Mech， 2005， 35（1）： 520.

[10]中国航空研究院. 应力强度因子手册[M]. 北京： 科学出版社， 1993： 11.