斜坡降雨入渗迭代计算模型研究
檀 康,简文星
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
斜坡降雨入渗迭代计算模型研究
檀 康,简文星
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
降雨是诱发斜坡失稳的最主要因素之一,研究降雨对斜坡稳定性的影响,其难点是如何计算降雨入渗过程中斜坡土体渗流场的变化规律。但是,从入渗量角度建立的传统田间入渗模型未考虑坡角的影响,无法满足斜坡稳定性的分析要求。基于Richard二维渗流控制方程与Parlange解法,从土体基质吸力水头角度推导出斜坡降雨入渗的迭代计算模型。该模型可以计算出低强度降雨条件下斜坡土体任意时间和空间的基质吸力,而且可以较为简便地计算出高强度降雨条件下斜坡表面积水时刻。利用有限元数值模拟软件对迭代计算模型进行验证,证明了此模型的适用性和准确性。
斜坡;降雨入渗;土体基质吸力;迭代;计算模型
降雨是诱发斜坡失稳的最主要因素之一,研究降雨诱发斜坡失稳机理并建立定量的分析模型对滑坡预测预防工作具有重要的指导意义。理论与实践表明,降雨诱发土质斜坡失稳的关键原因是土体基质吸力降低,进而导致其抗剪强度降低,直至斜坡失稳[1-3]。关于土体基质吸力对其抗剪强度贡献的研究取得了丰富成果,如Bishop[4]的有效应力原理,Lu等[5]的吸应力原理。只要能准确地刻画降雨条件下斜坡土体基质吸力的时空分布规律,就能运用较为成熟的强度理论准确地对降雨诱发斜坡失稳进行评价,因此对斜坡降雨入渗模型的研究具有重要的实际意义。
入渗模型一直以来备受土壤学家的关注,传统入渗模型有Green-Ampt积水入渗模型、Horton经验入渗模型和Philip入渗公式等[6]。这些模型多被用于农田灌溉研究中,故更注重入渗量、入渗速率和土壤含水量的刻画,而且模型边界条件多为地表土体饱和,即积水入渗条件,未考虑降雨入渗这类特殊条件[7]。小强度降雨条件下,入渗边界条件为地表通量已知,这些传统入渗模型无法适用。其次,传统入渗模型也未考虑坡角对入渗过程的影响,无法适用于斜坡场地的入渗过程分析。
针对以上不足,李宁等[8]基于Green-Ampt模型对Mein-Larson降雨入渗模型进行了改进,此模型可以反映坡面倾斜和降雨强度小于土体饱和渗透系数时的入渗过程分析,但此模型假定低强度降雨条件下,传导区含水量均匀分布,这与实际情况不符;Srivastava等[9]、詹良通等[10]、李宁等[11]采用指数函数描述非饱和土体的土-水特征曲线和渗透系数函数,建立了无限长斜坡降雨入渗的解析解法,但此方法需要求解较为复杂的级数;王建新等[12]基于Richard一维渗流控制方程推导出垂直降雨入渗水势模型,此模型可以刻画降雨条件下斜坡土体基质吸力的时空变化过程,但未考虑坡角的影响,无法适用于斜坡条件下的降雨入渗计算。
为能更好地刻画降雨入渗引起斜坡土体渗流场的变化,本文基于Richard二维渗流控制方程,运用Parlange解法的基本原理,推导出斜坡降雨入渗的迭代计算模型,最后利用有限元数值模拟软件对该模型的适用性和准确性进行了验证。
1 降雨入渗条件下斜坡内水分运移模型
1.1 假设条件
(1) 假定斜坡的长度为无限长。由于降雨诱发滑坡多为浅层滑坡,滑动面通常显著小于斜坡长度,故该假设是适用的。
(2) 假定地下水位较深,土体基质吸力较大,初始基质吸力为定值h0,降雨对地下水位的影响较小。对于干旱地区,如黄土地区,地下水位较深,土体较为干燥,考虑降雨条件下斜坡短期入渗行为,不会引起地下水位的显著上升,故该假设是适用的。
(3) 假定降雨条件下,土体基质吸力变化等值线平行于坡面。目前大多研究表明,斜坡在吸湿条件下,斜坡渗流路径为垂直斜坡表面,故该假设是适用的。
(4) 模型考虑的是一场均匀降雨。
1.2 斜坡降雨入渗控制方程
Richard最早根据质量守恒原理和达西定律推导出均质土体二维渗流控制方程。笛卡尔坐标系下,均质土体的二维非饱和渗流控制方程为
(1)
式中:k为坡体水平方向和竖直方向的渗透系数;h为坡体基质吸力水头;t为时间;C(h)为比水容量。
如图1所示为二维坐标下的无限长斜坡,其中x和z为标准笛卡尔坐标系,x*和z*为旋转后的坐标系,两坐标系之间的关系为
(2)
式中:γ为斜坡坡角(°)。
将式(2)代入式(1)并根据假定条件(2),坡体基质吸力水头h只随t和z*改变,故式(1)可化简为
(3)
为后面推导方便,用z*为因变量对式(3)进行变换,根据多元函数求导理论,式(3)可变为
(4)
1.3 基于Parlange解法求解斜坡降雨入渗控制方程的迭代公式
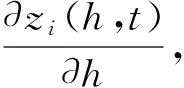
根据Parlange解法的基本原理,式(4)可变为
(5)
对式(5)进行积分,积分限由h0至h,根据假设条件(2),坡体初始基质吸力水头h0较大,对应的渗透系数k(h0)≈0,故积分整理得到
(6)
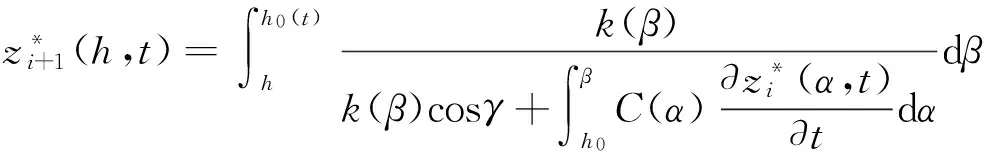
(7)
式(7)即为求解斜坡土体非饱和渗流控制方程的迭代公式。
2 斜坡降雨入渗模型
当降雨强度小于斜坡土体饱和渗透系数时,雨水全部入渗到坡体内,坡面不产生径流;当降雨强度大于斜坡土体饱和渗透系数条件初期,坡面基质吸力、水力梯度较大,土体入渗能力很强,超过降雨强度,此时雨水全部入渗到坡体内,坡面不产生径流。即在这两种情况下,斜坡入渗边界条件为通量控制条件[14]。基于以上分析可将斜坡降雨入渗过程概化为如下数学模型:
(8)
(9)
设h0(t)为随时间变化的地表基质吸力水头,对式(9)积分,积分限由h至h0(t),可得
(10)
对式(10)求t的导数 ,可得
(11)
将式(11)代入式(8),可得
(12)
对式(12)进行积分,积分限由h0至h,可得
(13)
通常h0较大,k(h0)≈0,所以式(13)可改写为
(14)
取h=h0(t)代入式(14),可得
(15)
化简式(15),可得
(16)
式(16)是一个关于h0(t)的常微分方程,对其进行求解,可得
(17)

3 迭代计算模型的验证与分析
为验证上述迭代计算模型的适用性和准确性,本文通过实例对其进行验证。
如图3所示,实例斜坡非饱和土层的垂直厚度为2 m,斜坡水平长度为20 m,斜坡倾角为30°,斜坡垂直厚度远小于水平长度,斜坡可假定为无限长。斜坡土体的初始基质吸力为200 kPa,土体较为干燥,不考虑地下水位的影响。
土体的土-水特征曲线和渗透系数函数是描述土体非饱和渗流的两个重要方程,参照文献[10],计算中土体的土-水特征曲线和渗透系数函数均采用指数函数形式来描述:
k(h)=kseαh
(18)
θ=θr+(θs-θr)eαh
(19)
斜坡土体相关参数的选取见表1,相应的斜坡土体土-水特征曲线和渗透系数函数曲线见图4和图5。

表1 斜坡土体相关参数的选取
有限元数值模型通过Geo-seep软件实现。有限元模型设定时间步长为60s,空间步长为0.01m,模型共计有8 421个节点、8 000个单元。模型上边界设定为流量边界,流量q=Rcosγ=1.15×10-5m/s,模型左右边界和下边界设定为自由透水边界。
图6给出了不同时刻迭代计算模型和有限元数值模型模拟得到的孔隙水压力沿垂直坡面的分布情况。由图6可见:两种计算模型的结果基本吻合,随着时间的推移,斜坡土体中的基质吸力不断减小,降雨对孔隙水压力的影响深度逐渐增大,当某一深度处的土体的抗剪强度不足以维持坡体稳定性时,可能会在该处发生坡体滑动。
为进一步验证迭代计算模型的正确性,对降雨强度大于斜坡土体饱和渗透系数情况下,坡面产生积水(或径流)的时刻两种模型的计算结果进行了对比分析(见表2)。积水时刻通过文献[9]中的方法进行确定,即地表基质吸力为0的时刻。有限元数值模型因为要设定一定的时间步长,因此其积水时刻不能精确得出,只能根据斜坡表面基质吸力为0出现在两个时间节点之间来确定,若要精确地确定积水时刻需要较小的时间步长,进而增加计算时间;而迭代计算模型只需通过式(17)即可计算得出,其计算较为简便、快捷。

表2 两种模型积水时刻计算结果对比
综上所述,迭代计算模型具有较好的准确性,而且可以简便地计算出高强度降雨情况下坡面积水(或径流)时刻。这是因为对于裂隙发育的斜坡,坡面产生径流之前可将斜坡当作均质斜坡处理,而坡面产生径流之后,裂隙处充水,需在裂隙处设置水头边界,而迭代计算模型为此提供了极大方便。但迭代计算模型为无限长斜坡入渗模型,只适用于坡面形态简单的浅层滑坡,而且没有考虑长时间高强度降雨工况。
4 结 论
基于Richard二维渗流控制方程与Parlange解法,推导出斜坡降雨入渗的迭代计算模型,该模型可以确定降雨条件下不同时刻不同深度处斜坡土体基质吸力的变化值。通过将其与有限元数值模型的计算结果进行对比,从而验证了该模型的适用性和准确性。迭代计算模型的计算结果可以用于评价降雨入渗对斜坡土体基质吸力与斜坡稳定性的影响,而且利用此模型还可较为简便地计算出高强度降雨条件下坡面积水时刻,为分析裂隙发育斜坡的入渗过程提供了便利。
[1] 卢宁,力科思.非饱和土力学[M].北京:高等教育出版社,2012.
[2] 杨矫,王宇,雷富宏,等.降雨入渗下残坡积土边坡的稳定性模拟研究[J].安全与环境工程,2012,19(3):5-10.
[3] 张久龙,孟繁贺,杨虎锋,等.降雨条件下某堆积体饱和-非饱和渗流及稳定性分析[J].安全与环境工程,2012,19(1):4-8.
[4] Bishop A W.ThePrinciplesofEffectiveStress[M].Sognsveien:Norges Geotekniske Institutt,1960.
[5] Lu N,Likos W J.Suction stress characteristics curve for unsaturated soils[J].JournalofGeotechinicalandGeoenvironmentalEngineering,2006,132(2):131-142.
[6] 雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社,1988.
[7] 简文星,许强,童龙云.三峡库区黄土坡滑坡降雨入渗模型研究[J].岩土力学,2013,34(12):3527-3533.
[8] 李宁,许建聪,钦亚洲.降雨诱发浅层滑坡稳定性的计算模型研究[J].岩土力学,2012,33(5):1485-1491.
[9] Srivastava R,Yeh T C J.Analytical solutions for one-dimensional,transient infiltration toward the water table in homogeneous and layered soils[J].WaterResourcesResearch,1991,27(5):753-762.
[10]詹良通,贾官伟,陈云敏,等.考虑土体非饱和特性的无限长斜坡降雨入渗解析解[J].岩土工程学报,2010,32(8):1214-1220.
[11]李宁,许建聪.无限长均质斜坡降雨入渗解析解[J].岩土工程学报,2012,34(12):2325-2330.
[12]王建新,刘晓丽,王恩志.垂直降雨入渗水势模型的推导及其试验验证[J].水文地质工程地质,2013,40(2):24-29.
[13]Parlange J Y.Theory of water movement in soils:8.One-dimensional infiltration with constant flux at the surface[J].SoilScience,1972,114(1):1-4.
[14]朱伟,程南军,陈学东,等.浅谈非饱和渗流的几个基本问题[J].岩土工程学报, 2006,28(2):235-240.
[15]黄润秋,戚国庆.滑坡基质吸力观测研究[J].岩土工程学报,2004,26(2):216-219.
[16]姚海林,郑少河,陈守义.考虑裂隙及雨水入渗影响的膨胀土边坡稳定性分析[J].岩土工程学报,2001,23(5):606-609.
[17]吴礼舟,黄润秋.考虑地表变流量的非饱和土渗流耦合的解析分析[J].岩土工程学报,2011,33(9):1370-1375.
[18]刘礼领,殷坤龙.暴雨型滑坡降水入渗机理分析[J].岩土力学,2008,29(4):1061-1066.
[19]朱伟,陈学东,钟小春.降雨入渗规律的实测与分析[J].岩土力学,2006,27(11):1873-1879.
[20]黄润秋,戚国庆.非饱和渗流基质吸力对边坡稳定性的影响[J].工程地质学报,2002,10(4):343-348.
[21]徐全,谭晓慧,沈梦芬.降雨入渗条件下土质边坡的稳定性分析[J].岩土工程学报,2012,34(S1):254-259.
[22]林志红,项伟,吴琼.库水位涨落和降雨入渗作用下岸坡中浸润线的计算[J].安全与环境工程,2008,15(4):22-26.
Research on Iterative Calculation Model of Slope Rainfall Infiltration
TAN Kang,JIAN Wenxing
(FacultyofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China)
Rainfall is one of the most important factors of slope failure.The key difficulty of studying the effect of rainfall on slope stability is how to calculate the process of rainfall infiltration.But the raditional field infiltration model which is established from the perspective of cumulative infiltration fails to consider the effect of slope angle,and can't meet the requirements of slope stability analysis.From the point of matrix suction head and based on the Richard seepage control equation and Parlange solution method,this paper establishes an iterative calculation model of slope rainfall infitration.The model can calculate the matrix suction of slope at any time and any space under the condition of low intensity rainfall,and can calculate slope surface ponding time easily under the condition of high intensity rainfall.Finally,the paper verifies the iterative calculation model with finite element numerical simulation software and proves that the model is feasible.
slope;rainfall infiltration;soil matrix suction;iteration;calculation model
1671-1556(2015)04-0168-05
2015-01-21
2015-03-03
国家自然科学基金项目(41272306);国土资源部黄土地质灾害重点实验室开放基金项目(GLA2014002)
檀 康(1990—),男,硕士研究生,主要研究方向为饱和-非饱和渗流方面的研究。E-mail:tankangmove@163.com
X93;P642
A
10.13578/j.cnki.issn.1671-1556.2015.04.030

