半充填裂隙渗流应力特性的微结构效应
张 泷,陈金刚,2,3,韩建军
(1.郑州大学力学与工程科学学院,河南 郑州 450001;2.中国矿业大学煤炭资源与安全开采国家重点实验室,江苏 徐州 221116;3.河南省瓦斯地质与瓦斯治理重点实验室,河南 焦作 454003;4.河南工业大学土木建筑学院,河南 郑州 450001)
半充填裂隙渗流应力特性的微结构效应
张 泷1,陈金刚1,2,3,韩建军4
(1.郑州大学力学与工程科学学院,河南 郑州 450001;2.中国矿业大学煤炭资源与安全开采国家重点实验室,江苏 徐州 221116;3.河南省瓦斯地质与瓦斯治理重点实验室,河南 焦作 454003;4.河南工业大学土木建筑学院,河南 郑州 450001)
针对填充物在渗流应力作用下破裂过程的非稳定性问题,应用突变理论建立了半充填裂隙破坏失稳的尖点突变模型,导出了半充填裂隙破坏失稳的充要条件表达式,证明了当应力满足突变模型的分叉点集方程时,其相对应的孔隙的微结构将发生失稳坍塌;利用试验仪器对半充填裂隙进行了渗流试验研究,通过分析整理试验数据,得出半充填裂隙的渗流应力曲线,并将试验数据与微结构突变失稳假说相结合,比较理论计算值与试验实测值,发现两者具有较高的吻合性,说明以微结构失稳的尖点突变理论为基础来研究半充填裂隙在渗流应力作用下的破坏失稳是可靠的。
微结构;尖点突变模型;半充填裂隙;渗流;应力
在天然条件下裂隙被介质充填是一种较为普遍的现象,充填物对裂隙的渗流起着重要的影响,对于这方面的研究,前人现已有诸多成果。如陈金刚等[1]研究了充填物拉张效应、剪切效应、塑化效应和液化效应对裂隙的渗透性影响;王甘林等[2]通过对充填泥砂裂隙岩石进行渗流特性试验研究,总结出泥沙颗粒对裂隙岩石渗透性的影响规律;陈义等[3]应用有限元分析软件对裂隙全充填的岩体进行了数值模拟计算,结果表明裂隙充填物的膨胀效应增大了裂隙岩体各应力的分量。
突变理论是由比利时数学家Thom创立的,近年来,一些学者利用突变理论对自然界中的诸多突变现象进行了研究。如Miao等[4]应用突变理论提出了湿陷性的微结构突变失稳假说,认为物质的湿陷变形是由微结构失稳所引起。本文对半充填裂隙进行了渗流试验,通过分析整理试验数据,得出半充填裂隙的渗流应力曲线,并将试验数据与微结构突变失稳假说相结合,比较理论计算值与试验实测值,发现两者具有较高的吻合性,从而对充填物微结构的崩塌变形给予了合理的数学描述。
1 尖点突变理论的数学模型
突变理论是以拓扑学、奇点理论为数学工具,用来研究各种突变的理论。R.Thom 的研究表明,在控制变量不大于4、状态不大于2的情况下最多可有7种基本突变模型[5],其中尖点突变模型是突变理论中最简单、最实用的模型,具有2个控制变量和一个状态变量,其势函数的标准形式为[6]
V(x)=x4+px2+qx
(1)
式中:x为系统状态变量;p、q为控制变量,(p,q)所在平面为控制平面,(x,p,q)构成三维空间。
将式(1)分别进行一阶和二阶导数求导并联立消去x,得到系统突变的分叉集方程为
8p3+27q2=0
(2)
当系统的控制参数满足式(2)时,系统将处于临界平衡状态并且最终要突跳到稳定的平衡态,完成系统的突变。
2 充填物破坏失稳的尖点突变模型
可采用简单结构元来模拟充填物微结构架空孔隙[7],将固体颗粒简化为刚性杆,杆与杆之间的粘结关系由弹簧来模拟,弹簧刚度系数为K,见图1。
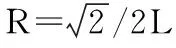
V(θ)=2Kθ2+2R2[σcosθ-τsinθ-σ]
(3)
令τ≠0,为得到突变理论模型,将式(3)在θ=0点展开,有
(4)
化简后得
(5)
对式(5)求导可得系统的平衡方程:
(6)
经计算得
(7)
(8)
则分歧点集(失稳判定条件)为
Δ=8p3+27q2=9KR4τ2-4(R2σ-2K)3=0
(9)
当应力水平满足此孔隙微结构失稳判别式时,填充物被破坏。
3 半充填裂隙渗流试验
3.1 试验装置和测试方法
半充填裂隙渗流试验在郑州大学力学实验中心进行,试验中裂隙壁采用与变形试验试件同规格的的水泥砂浆长方体模拟(长、宽、高尺寸分别为L=100 mm、b=50 mm、h1=h2=20 mm),见图2。
裂隙壁配制比为水泥∶砂∶水=1∶2∶0.5,裂隙充填物为水泥砂浆,水泥∶砂∶水配制比分别为1∶2∶0.5、1∶4∶0.5、1∶6∶0.5、1∶8∶0.5,充填物宽度分别设置为10 mm、15 mm、20 mm,厚度为20 mm。试验所采用的主要装置有微机控制万能材料试验机、流量计、水箱、水管、阀门等,见图3。
试验前,为使试件的端面平整光滑且满足几何尺寸的要求,采用磨砂纸将试件磨光,在对充填裂隙法向施压的同时通过上水箱提供裂隙渗流。试验时,对充填裂隙侧限约束,以法向加载为主控参数,加载速率为0.2 mm/min,将样品放入钢槽内,再把钢槽放到试验台上并调整好,将压头平整压入钢槽,使用微机控制万能材料试验机输入载荷,在每级荷载下,静止等待大约5 min,待水流流速稳定后分别记录样品所受荷载、法向位移、上下流量计的流量读数,反复持续操作直到上下流量计读数稳定。待测试结束后,关闭阀门,并拆除试验装置。
3.2 渗流试验结果与分析
本次共进行了多组非充分充填裂隙渗流试验,得到的试验结果见图4。
由图4可以看出:多组试验样品所得数据具有相似规律性,在一定的法向应力作用下,裂隙面会发生一定的闭合,即裂隙宽度减小,从而使裂隙的渗流量发生了变化,也即裂隙渗流量随法向应力的增大而呈现出明显的非线性减小趋势,可以划分为三个阶段:平稳阶段、失稳阶段和稳定阶段。
平稳阶段:试验开始为低应力阶段,应力作用在充填介质和裂隙壁上,由于应力是逐渐增大的,开始阶段所施加的应力还不足以使充填介质发生突变,对充填介质影响不大,因此通过裂隙的渗流量保持平衡状态。
失稳阶段:随着应力增大,充填介质在应力的某个临界点发生突变,充填介质颗粒软化棱角破碎、相互滑移、重新分布填充等,最终导致颗粒的相互错动和位移,进而充填到自身孔隙、裂隙空间的厚度明显变小,导致轴向方向上裂隙内部充填介质颗粒间的结构变得更加致密,最终导致通过该裂隙的渗流量突然变小[10-11]。
稳定阶段:在裂隙水和法向压力持续作用下,裂隙壁及充填介质进一步被压密,呈现应变硬化,裂隙间距达到最小,施加的应力与裂隙壁的弹力达到平衡,裂隙的渗流量变化极为缓慢,最终处于稳定状态。
另外,分析图4还可以看出:同一配制比的水泥砂浆充填裂隙,裂隙充填物宽度大的初始阶段高渗流量持续时间长;初始阶段随着裂隙充填物宽度的增大,同一充填介质在同一渗流量时刻所对应的应力值有增大的规律;当在同一裂隙充填物宽度下进行渗流试验时,充填物泥砂配制比从1∶2~1∶8变化的过程中,裂隙渗流量趋近于稳定时所对应的应力值减小,这是因为充填物泥砂配制比越低,颗粒之间的黏聚力越弱,内部结构稳定性越差。
3.3 充填裂隙失稳破坏应力计算值与实测值对比
本试验制备了多种规格裂隙充填物,不同规格水泥砂浆半充填裂隙渗流应力参数统计见表1。
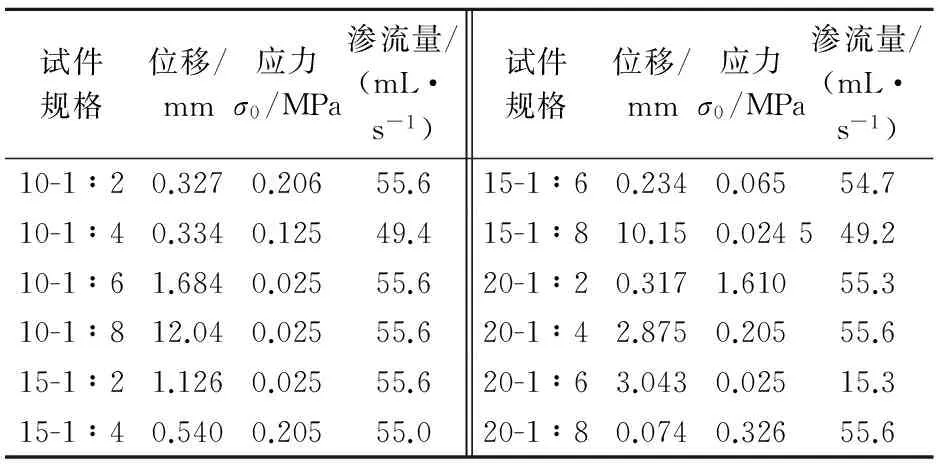
表1 不同规格水泥砂浆半充填裂隙渗流应力参数统计
为了深入全面地分析试验结果,将表1各项参数代入应力-应变关系式:ε=Δb/b,E=σ0/ε[式中:ε为应变;Δb为位移(mm);b为原长(mm);E为裂隙充填物的变形模量(MPa);σ0为试验过程所施加的应力(MPa)],可以计算得到裂隙充填物的变形模量E。
水可以降低充填物的变形模量,熊德国等[12]通过试验研究发现,饱水状态砂质泥岩的变形模量降低系数为0.58~0.62。本试验裂隙充填物水泥砂浆的含水率是从0%~100%逐步递增的,根据水泥砂浆的特性,试验过程中随着水流的持续通过,水泥砂浆由干燥状态变为饱和状态,其强度衰减明显。将计算所得裂隙充填物变形模量E乘以变形模量降低系数,即可得到半充填裂隙遇水软化崩解时的变形模量E1,见表2。

表2 半充填裂隙的变形模量E1
由K=EA[式中:K为刚度系数;A为横截面面积(mm2)],可将微结构失稳的判别公式[式(9)]化简为
9πEσ2-4(σ-2πE)3=0
(10)
将表2所求得的半充填裂隙变形模量E1代入式(10),即可计算得到不同规格水泥砂浆半充填裂隙失稳破坏的应力σ。为了验证上述所求应力的合理性,本文将应力计算值与实测值进行了对比,详见表3。
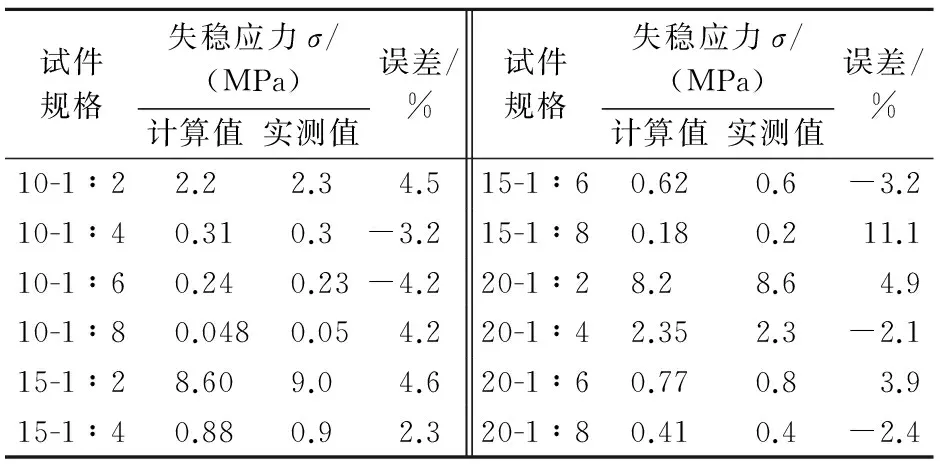
表3 半充填裂隙失稳破坏应力计算值与实测值的对比
通过分析对比发现,水泥砂浆半充填裂隙失稳破坏所受应力的计算值与实测值之间的相对误差的绝对值小于5%的约占92%,在误差允许的范围内,因此可以应用尖点突变理论来计算水泥砂浆遇水破坏所受的应力。
4 结 论
本文利用尖点突变理论方法对不同规格水泥砂浆半充填裂隙在法向应力加载条件下遇水破坏失稳的现象进行了理论分析,并对半充填裂隙进行了渗流试验,通过理论与试验分析得出以下结论:
(1) 半充填裂隙渗流应力曲线表现出平衡阶段、失稳阶段和稳定阶段三个阶段。试验开始时,通过裂隙的渗流量保持平衡状态;当应力增大到临界值,裂隙渗流量突然减小;随着应力继续增大,裂隙渗流量最终趋于稳定。
(2) 应用突变理论建立了半充填裂隙破坏失稳的尖点突变模型,推导出了半充填裂隙破坏失稳的充要条件表达式, 理论计算结果表明:水泥砂浆浸水湿化后,其变形模量降低,使得半充填裂隙逐渐向不稳定区靠近,当应力水平满足孔隙微结构失稳判别式时,充填物被破坏,半充填裂隙发生失稳。
(3) 通过渗流试验研究了半充填裂隙渗流应力特性,理论计算和试验结果对比分析表明:利用尖点突变理论计算所得的半充填裂隙失稳破坏应力值与试验实测值具有较好的吻合性,说明以微结构失稳的尖点突变理论为基础来研究半充填裂隙在渗流应力作用下的破坏失稳是可靠的。
[1] 陈金刚,张景飞.充填物的力学响应对裂隙渗流的影响[J].岩土力学,2006,27(4):577-580.
[2] 王甘林,刘卫群,陶煜.充填泥沙裂隙岩石渗流特性的实验研究[J].力学与实践,2010(5):14-17.
[3] 陈义,王传琪,陈金刚.基于ANSYS的裂隙岩体全充填介质膨胀效应的数值模拟[J].安全与环境工程,2012,19(4):115-119.
[4] Miao T D,Liu T D,Niu Z Y.Unified catastrophic model for collapsible loess[J].JournalofEngineeringMechanics,ASCE,2002,128(5):595-598.
[5] 郭文斌,邓喀中.走向条带煤柱破坏失稳的尖点突变模型[J].岩土力学与工学学报,2004,23(12):1996-2000.
[6] 邓跃进,董兆伟,张正禄.大坝变形失稳的尖点突变模型[J].武汉测绘科技大学学报,1998,24(2):107-110.
[7] 孙强,张晓科,李厚恩.湿陷性黄土变形的微结构突变模型研究[J].岩土力学,2008,29(3):663-666.
[8] 朱彦鹏,王婧.尖点突变模型在湿陷性黄土微结构失稳中的应用[J].兰州理工大学学报,2012,38(6):103-107.
[9] 苗天德.湿陷性黄土的变形机理与本构关系[J].岩土工程学报,1999,21(4):384-387.
[10]Barton D E,Quadros F.Joint aperture and roughness in the prediction of flow and groutability of rock masses[J].InternationalJournalofRockMechanicsandMiningSciences,1997,34(3):700-713.
[11]Koyama T,Li B,Jiang Y,et al.Numerical modelling of fluid flow tests in a rock fracture with a specia al gorithm for contact areas[J].ComputersandGeotechnics,2009,36(1/2):291-303.
[12]熊德国,赵忠明.饱水对煤系地层岩石力学性质影响的实验研究[J].岩石力学与工程学报,2011,30(5):998-1006.
Effect of Microstructure on Seepage-stress Characteristics of Half-filled Fracture
ZHANG Long1,CHEN Jingang1,2,3,HAN Jianjun4
(1.SchoolofMechanics&EngineeringScience,ZhengzhouUniversity,Zhengzhou450001,China; 2.StateKeyLaboratoryofCoalResourcesandMineSafety,ChinaUniversityofMining&Technology,Xuzhou221116,China;3.StateKeyLaboratoryCultivationBaseforGasGeologyandGasControl,Jiaozuo454003,China;4.SchoolofCivilEngineeringandArchitecture,HenanUniversityofTechnology,Zhengzhou450001,China)
Faced with the problem that the filling is unstable under the action of seepage and stress process,this paper establishes a cusp catastrophe model for the instability of half-filled fracture based on the catastrophe theory,derives the sufficient and necessary condition expression of the instability of half-filled fracture,and proves that instable collapse of the corresponding pore microstructure will occur if the stress meets the bifurcation set equation of the catastrophe model.The paper studies the failure of half-filled fracture which is under the action of seepage and stress process by using laboratory equipment and obtains seepage-stress relationship curves of half-filled fracture based on experimental data.It is found that the experimental data agrees well with that of the theory.The study indicates that microstructural instability of the cusp catastrophe theory may be applied to half-filled fracture research,and that the method is reliable.
microstructure;cusp catastrophe model;half-filled fracture;seepage;stress
1671-1556(2015)04-0160-04
2014-11-20
2014-12-20
中国矿业大学煤炭资源与安全开采国家重点实验室项目(13KF04);河南省瓦斯地质与瓦斯治理重点实验室项目(WS2013A04);河南省教育厅科学技术研究项目(12B410003、2011B410004)
张 泷(1988—),男,硕士研究生,主要研究方向为充填裂隙水力特性。E-mail:18239905116@163.com
X93;P
A
10.13578/j.cnki.issn.1671-1556.2015.04.028
陈金刚(1973-),男,博士,教授,主要从事充填裂隙水力特性等方面的研究。E-mail:chenjg@zzu.edu.cn

