火柴棒游戏

姜红

一、 活动背景

荷兰数学教育家弗赖登塔尔说：“数学学习是一种活动，这种活动与游泳、骑自行车一样，不经过亲身体验，仅仅靠看书本、听讲解、观察他人的演示是学不会的.”我们的新课程标准中也提出了“基本活动经验”的新目标.其中还具体指出“学生应当有足够的时间和空间经历操作、观察、模仿、实验、猜想、验证等活动过程“.所以说“动手实践”也是学习数学的一种重要方式.

二、 实验目的

通过动手操作与思考活动，提高对一些基本图形的认识能力， 并渗透对“图形运动”的理解，帮助同学们直观感受几何图形.

三、 实验准备与要求

准备火柴棒（或等长小木棒）若干. 本课实验需要同学们按要求搭出符合条件的图形. 在操作过程中要积极思考，并与同学交流. 实验活动过程中不可以将火柴棒折断，或者部分使用. 要用完整的火柴棒达到实验要求.

四、 活动过程

在我们小的时候，会用火柴棒搭一些象形的图案，从中我们享受了无穷的乐趣. 在小学里，我们又用火柴棒搭一些有趣的算式，如：移动一根火柴棒，使等式成立.

你知道该怎么移动吗？

小小的火柴棒可以帮助我们学数学、增见识、长智慧.

1. 搭正方形

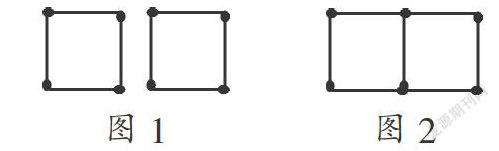
（1） 我们知道用8根火柴棒搭2个正方形；用7根火柴棒能搭2个正方形吗？ 你是如何想到的？

通过思考不难回答，要面积不变而火柴棒根数变少，必须让这两个图形共用某个边，即从图1变为图2.

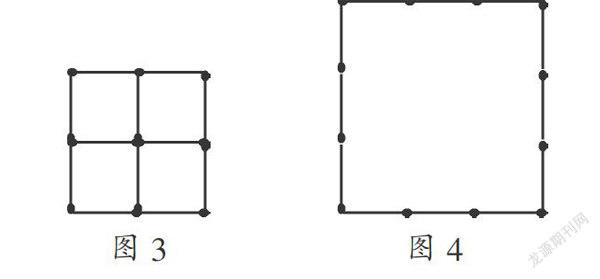
（2） 把1根火柴棒的长度记为1，用12根火柴棒能搭出面积分别为4、5、8 、9的正方形吗？

经过尝试可以搭成面积为4和9的正方形（如图3、图4），但是面积为5和8的正方形是搭不出来的.

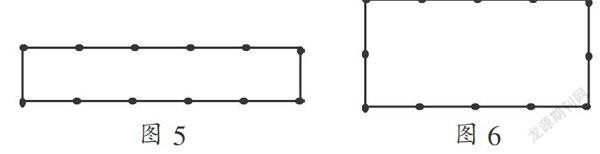
那么把问题（2）的要求稍做变化，用12根火柴棒能搭出面积分别为4、5、8 、9的图形吗？去掉了正方形的限制，稍作思考即可知道，这是可以做到的，如图5、图6.

这两个图形还可以从计算上去验证：

图5中，面积为：5×1=5，周长为：（5+1）×2=12；

图6中，面积为：4×2=8，周长为：（4+2）×2=12，故而均满足要求.

从另一个方面来想，既然已经可以搭成面积为9的正方形，而面积为8、5的图形没有形状限制，那么是否可以用减少其面积，但不减其周长来实现实验目的呢？容易得出把图4变为如下图7—图13，其面积从9依次减少到3.

思考以上移动火柴棒的实验，其本质是线段的平移，因此其长度不变，但所围成区域的形状及面积却发生了改变.

2. 搭三角形

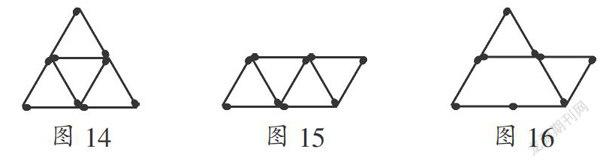
（1） 用9根火柴棒分别搭5个三角形、4个三角 形、3个三角形.其答案如图14、图15、图16.（注意其中有部分是叠合在一起的）

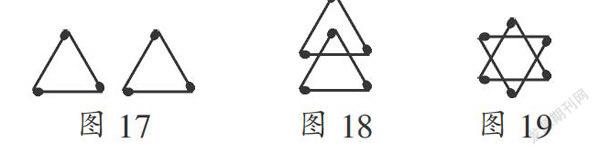
（2） 用6根火柴棒能搭2个三角形，如图17，那么能搭3个三角形吗？稍作思考可知不能，也不能搭出更多的三角形. 但是如果允许火柴棒交叉显然就可以实现，如图18中共有3个三角形、图19中有8个三角形. 允许交叉是思维上的一次突破.

3. 数学思考

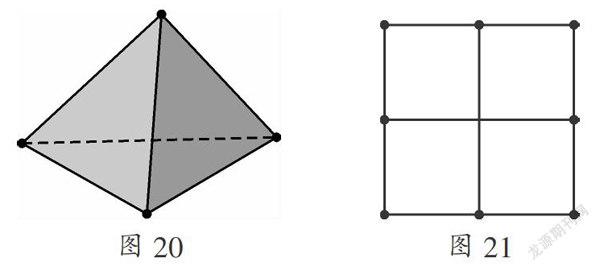
如果允许火柴棒搭成空间图形或者交叉，显然问题将更灵活、更发散，搭4个三角形最少只需要几根火柴棒呢？如图20，搭成一个空间里的正四面体，每个面都是三角形，但是只需要6根火柴棒； 搭5个正方形最少也只需要6根火柴棒，如图21，注意其中有重叠哦.

19世纪英国著名数学家德· 摩根有这样一句名言：数学发明创造的动力不是推理， 而是想象力的发挥. 本实验从用火柴棒搭符合一定条件的正方形开始，到搭满足要求的三角形以及其他图形，再到数学思考，从平面视角到空间视角，我们能感受到小小的火柴棒蕴含着大智慧.善用数学实验，变“听”数学为“做”数学，通过做数学实验体验发现的乐趣，感悟数学真谛，在发展数学思维的同时提高实践能力，相信同学们以后可以把数学学得更好.

（作者单位：江苏省南师附中江宁分校）