数学思想应适时渗透、不断深入和逐步“领悟”

邱小琴

使学生获得数学的基本思想是数学课程的重要目标。数学思想是学生数学学习的灵魂，数学思想方法数是数学的灵魂所在，掌握一定的数学思想方法不仅可以使学生更透彻地理解数学知识，对学生的数学学习产生持久的推动力，而且是培养学生创新思想和实践能力的坚实基础。数学思想是数学教学的核心和精髓，教师在讲授数学方法时应尽力反映和体现数学思想，让学生了解和体会数学思想，提高学生的数学素养。

一、数学思想的形成需要在过程中实现

只有经历问题解决的过程，才能体会到数学思想的作用，才能理解数学思想的精髓，才能进行知识的有效迁移。

案例一：五年级的估算教学

……

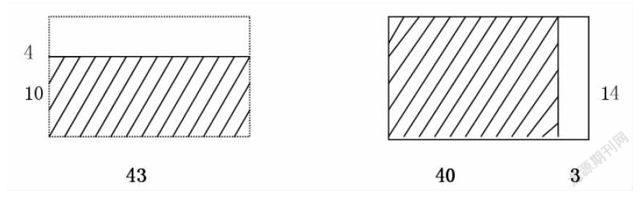
师：估算43×14 你是怎么估的？

生：我把43估为40，40×14=640。

另一位学生又说：我把14估为10，43×10=430。

师：那到底哪个值更接近准确值呢？为什么两个值会相差这么大呢？

先在小组讨论，指名汇报。

过了好一会儿，终于有个学生站起来说：因为43少估了3，也就是3个14，而14少了4，也就是4个43。可大部分学生还是不理解，这时教师出示了两幅图：

学生这时恍然大悟，哦，原来是这样。用图进行比较真是一目了然。在课的最后进行总结时，教师问：今天你最难忘的是什么？学生回答说，老师用图来比较40×14和43×10为什么相差这么大，让我最难忘。

在这节课中，数形结合思想能不失时机地为学生提供恰当的形象材料，把无形的解题思路形象化，更有效地理解算理，不仅有利于学生顺利、高效地学好数学知识，更有利于学生学习兴趣的培养、智力的开发、能力的增强，使教学收到事半功倍之效。如果教师的教学流于形式，学生的脑中就不会真正建立起“数和形”的联系。

二、数学思想重在感悟

教学中要让学生感悟数学思想和方法，关键是要让学生经历和体验一些数学知识的获取过程。

比如，“三角形的分类”的教学，先给学生类别的三角形的卡片，让学生分小组探讨如何对三角形进行分类，给出明确的分类标准，讨论同一类的判定、性质，不同三角形的关系。学生在思考和解决这样问题的过程中，不断对“如何进行分类”这个问题进行深入思考，并且在与其他同学进行探讨的过程中不断修正和调整自己的想法，逐步找到合理的分类标准。经历这样的过程，学生对“分类”思想的认识要比教师直接讲结论印象深刻得多。

再如，在一年级“认识图形”的教学中，教师提供给学生多种不同的物体，有长方体、正方体、球体、圆柱体，如各种包装盒、积木、茶叶筒等。教师把这些学具放到一起，放手让学生在学习小组中给这些物体进行分类。学生通过看一看、摸一摸、比一比、想一想、说一说、分一分等方法，从中抽象出四类物体：（1）长方体：有六个平平的面，有的长长的，有的方方的，相对的面都是相等的；（2）正方体：有六个平平的面，是方方的，六个面都是相等的；（3）圆柱体：有2个平平的面，1个弯弯的面；（4）球体：无论怎么看都是圆的，摸来到处是圆溜溜的，可以随便滚来滚去。在比较、分析中，学生把具有共同特征的物体归为一类，在分类中抽象出此类图形的共同特征。在这一探究活动中，学生经历了分类的过程，渗透了分类的思想、集合的思想、抽象概括的思想等多种数学思想，在掌握知识的同时还形成分类的基本策略，提高学生的数学素养。

三、数学思想的渗透

数学思想的渗透不是简单地告诉，而应是在教学中组织有效的数学素材，创设认知冲突，适时渗透数学思想，在亲历、交流中让学生获得终身发展所需的数学素养。

案例2：五年级的数学广角“植树问题”

1.课件出示：同学们在全长1000米的小路一边植树，每隔5米栽一棵，一共需要多少棵树苗？

师：从题目中你得到了什么信息？

师：你觉得种几棵比较合适？

生汇报：（学生可能会说200棵、201棵等）

2.师：能不能把你的思考过程用简单的线段图表示出来呢？如果用图表示究竟要选择什么样的数据来画呢？有的同学说，我们可以选择小一点的数据研究，看看棵树与间隔数存在什么关系，找到规律之后，就可以解决在1000米的路上植树的问题了。

3.同学们独立用练习纸上的线段图画一画，我们进行一次模拟植树活动怎么样？学生尝试。

学生汇报，并指明学生到黑板上把图画出来。

（1）说说你们是怎样研究的？你们选择的数据是多少？有没有更小一点的数据，也研究出了问题的？

（ 2）问什么加1？

4.回顾总结：我们刚才的问题解决经历了一个怎样的过程？

师：同学们把复杂的问题转化为简单的问题，从较小的数据开始研究，用画图的方法帮助我们发现种植棵树和间隔数的关系，再应用它们的关系说明复杂的问题，这些都是同学们学习方法上的收获。

在这节课的教学中，教师把数学思想方法以解决学生容易接受的实际问题的形式，通过实验、观察、操作、推理等数学活动进行渗透，让学生在活动中感悟，进一步提高学生的思维能力，激发解决问题的意识，获得解决问题的策略。教师把数学思想方法由暗线变明线，在学生通过解决问题感受到所蕴含的思想方法，再鼓励学生运用这一思想方法解决后面的问题。

总之，数学思想离不开具体的数学，空谈数学思想是没有意义的，数学知识与数学思想是紧密联系的。数学知识的发生、发展过程，也是数学思想的发生和凸显的过程。只有对数学内容进行深入思考，才能逐步体会其中蕴含的数学思想；只有对相关的数学内容进行联想、类比，才能感悟数学思想；只有不断思考问题，才能体会数学思想的作用。