平面向量中三点共线与线性规划的应用
2015-09-10 07:22郁得环
考试周刊 2015年42期
郁得环



摘 要: 对于平面向量中的三点共线结论:若x,y满足x+y=1,则得出A、B、P三点共线,反之也成立.解决平面向量的三点共线问题时,可以结合线性规划,将两者的内容融合起来合成一个有一定思维量的中档题型,有利于考查学生的思维能力和融会贯通能力.
关键词: 向量 现行规划 共线 最值 取值范围
一、对一道向量问题的改编
数学就是要研究一些问题,可以是别人探究过的,也可以是自己探究的,但总要有所发现.最近看《中学数学》,其中有这样一道题:
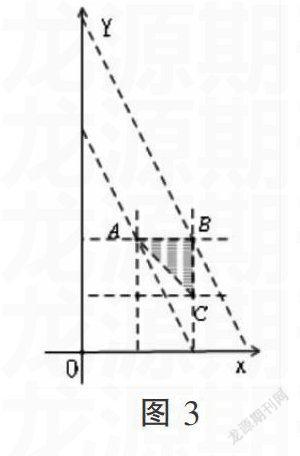
其解法如上,再加图3,利用线性规划的方法,不难得出2x+y在B点取得最大值为6,而在A点取得最小值为4.
这样一来,就可以把在高中数学中的两个不太大的问题融合成一个有一定思维量的中档题型,有利于考查学生的思维能力和融会贯通能力,是只会死做题的人很难想到的.
二、平面中三点共线与线性规划的应用
平面向量中三点共线还可以用在算两次的题型中,这里不再举例.总之,数学题目浩若烟海,类型繁多,但怎样使我们的学习与探索更有意义、更有效、发现更多的规律?这无疑是每一人都想做到的.那么,反思和总结必不可少.总结归类,从中抽取其共有规律,反思发现规律的历程,看哪些环节还可以精简,使我们的解答或证明更简洁、更完美,因为规律本身就是这样,当然它本质地反应在数学上,肯定很完美.
猜你喜欢
中学生数理化·高一版(2023年2期)2023-03-23
新高考·高一数学(2022年3期)2022-04-28
新高考·高一数学(2022年3期)2022-04-28
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中等数学(2021年4期)2021-08-14
中学生数理化(高中版.高考数学)(2021年1期)2021-03-19
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
高中生学习·高三版(2016年9期)2016-05-14

