2015年中考数学试题大预测
马建民



一、数与
1.(-2)x3的结果是().
A.一5
B.1
C.-6
D.6
2.设n为正整数’,且,则n的值为().
A.5
B.6
C. 7
D.R
3.如图1,已知正方形的边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是().
A.0.1
B.0.2
C.0.3
D.0.4
4.按如图2所示的程序计算,若开始输入的n值为则最后输出的结果是().
A.14
B.16
5.某商品先按批发价a元提高10%零售,后又按零售价降低10%出售,则它最后的单价是()元.
A.a
B. 0.99a
C.1.2la
D.0.8la
6.若是同类项,则m-3n的立方根是____.
7.观察下列各式:
8.先化简,再求值:其中a=-l.
9.若x>y,则下列式子中错误的是().
A.x-3>y-3
B.
C.x+3>y+3
D,-3x>-3y
10.在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是().
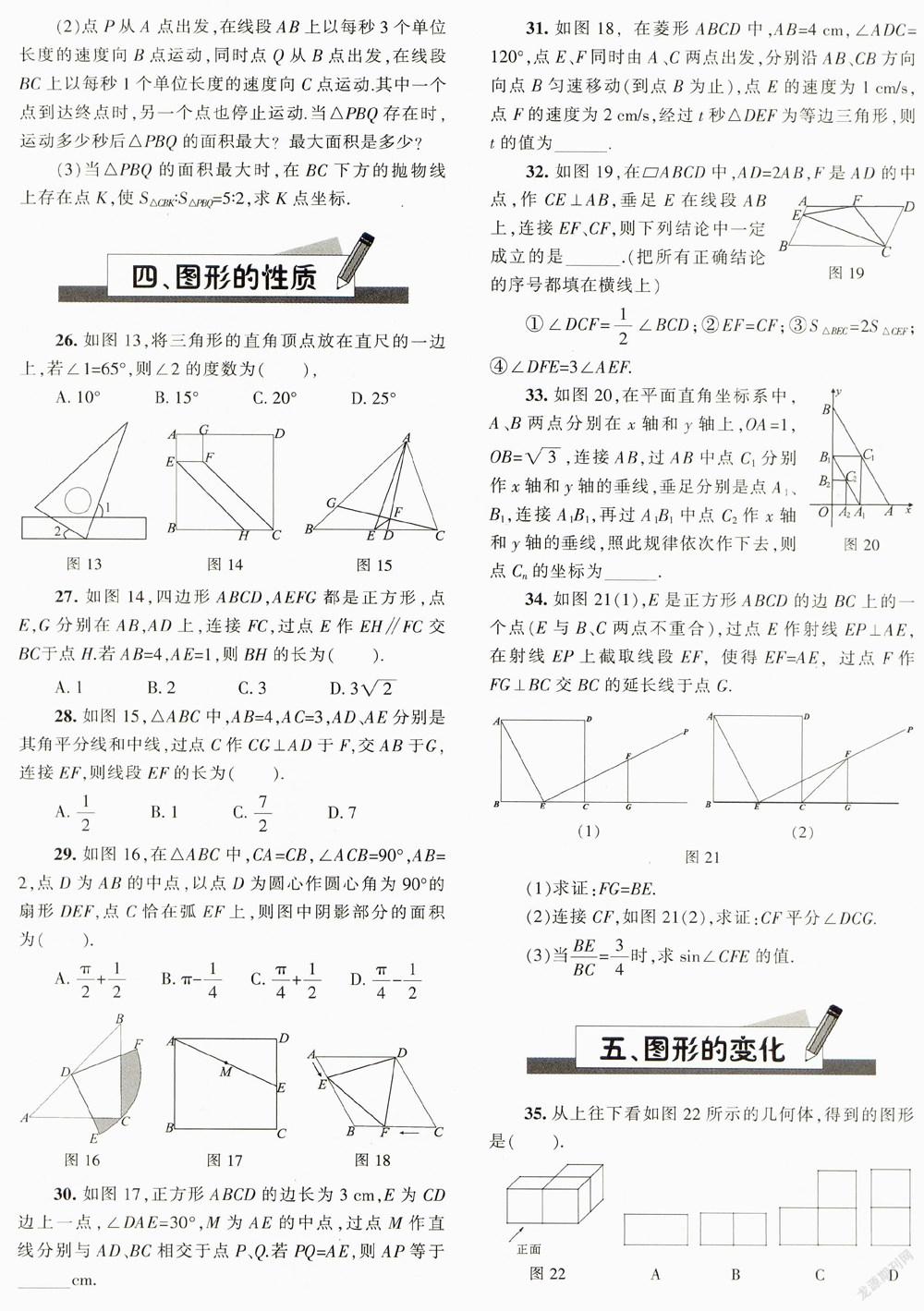
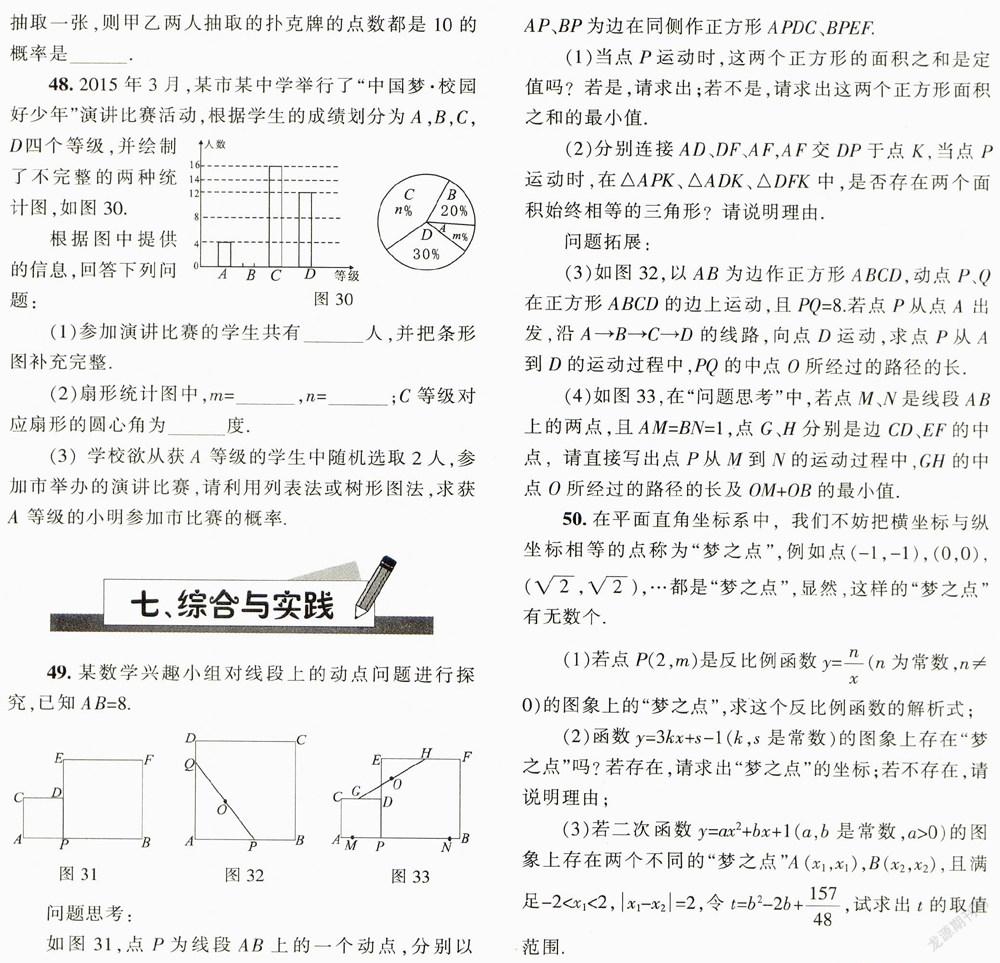
A.1cm B.5cm C.4cm D.4cm 11.某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1儿童节”举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出x支,则依题意可列得的一元一次方程为(). A. 1.2x0.8x+2x0.9(60+x)=87 B. 1.2x0.8x+2x0.9(60-x)=87 C. 2x0.9x+1.2x0.8(60+x)=87 D. 2x0.9x+1.2x0.8(60-x)=87 12.若是关于x的一元二次方程0的一个根,则a的值为(). A.1或4 B.-1或4 C.-1或-4 D.1或-4 13.方程的解为 ____. 14.不等式组的解集是____. 15.如图3,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各20克的砝码,现将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图4,则被移动的玻璃球的质量为____ 16.“保护好环境,拒绝冒黑烟”,某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元:若购买A型公交车2辆,B型公交车1辆,共需350万元. (1)购买A型和B型公交车每辆各需多少万元? (2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次,若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少? 三、函数 17. 2015年4月10日上午,小华同学接到通知,她的作文通过了《我的中国梦》征文选拔,需尽快上交该作文的电子文稿.接到通知后,小华立即在电脑上打字录入这篇文稿,录入一段时间后因事暂停,过了一小会,小华继续录入并加快了录入速度,直至录入完成.设从录入文稿开始所经过的时间为x,录入字数为y,下面能反映y与x的函数关系的大致图象是(). 18.如图5,A、B两点在双曲线上,分别经过A.B两点向坐标轴作垂线段,已知(). A.3 B.4 C.5 D.6 19.如图6,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿运动一周,则P点的纵坐标),与点P走过的路程s之间的函数关系用图象表示大致是(). 20.已知二次函数(a≠0)的图象如图7,则下列说法:①c=0;②该抛物线的对称轴是直线x=-l;③当x=l时,y=2a;④(m≠-1).其中正确的个数是(). A.1 B.2 C.3 D.4 21.如图8,已知直线与直线交于点A,它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点,则线段EF的长度为____. 22.如图9,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点c.设BE=x,BC=y,则y关于x的函数解析式是____. 23.如图10,在平面直角坐标系中,的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被截得的弦AB的长为,则a的值是 . 24.如图11,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线交于点P(-1,n),且F是PE的中点. (1)求直线l的解析式. (2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),当a为何值时,PA=PB? 25.如图12,在平面直角坐标系中,抛物线(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C. (1)求抛物线的解析式. (2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动.其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,运动多少秒后△PBQ的面积最大?最大面积是多少? (3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使,求K点坐标. 四、图形的性质 26.如图13,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为(), A.10° B.15° C.20° D.25° 27.如图14,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH//FC交BC于点H.若AB=4,AE=1,则BH的长为(). A.1 B.2 C.3 D. 28.如罔l5,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为(). 29.如图16,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF.点C恰在弧EF上,则图中阴影部分的面积为(). 30.如图17,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm. 31.如图18,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB.CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为____. 32.如图19,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是____(把所有正确结论的序号都填在横线上) 33.如图20,在平面直角坐标系中.A、B两点分别在x轴和y轴上,OA=l,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点C的坐标为 ____ . 34.如图21(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE.在射线EP上截取线段EF,使得EF=AE.过点F作FG⊥BC交BC的延长线于点G. (1)求证:FG=BE. (2)连接CF,如图21(2),求证:CF平分∠DCC. (3)当时,求sin∠CFE的值. 五、图形的变化 35.从上往下看如图22所示的几何体,得到的图形是(). 36.下面的图形中,既是轴对称图形又是中心对称图形的是(). A.正六边形 B.平行四边形 C.正五边形 D.等边三角形 37.将两个斜边长相等的直角三角形纸片如图23(1)放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图23(2),连接DiB,则∠E1D1B的度数为(). A.10° B.20° C.7.5° D.15° 38.如图24,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB'C’的位置,连接C’B,则C’B的长为(). 39.如图25.在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA’,则点A’的坐标是____ 40.如图26,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,线段AB为半圆0的直径,将Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,DF与BC交于点H.则Rt△ABC与△DEF重叠(阴影)部分的面积是____. 41.如图27,点P在以AB为直径的半圆内,连AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法正确的是:____.(填序号) ①AC垂直平分BF;②AC平分∠BAF;③PF⊥AB;④BD⊥AF. 42.如图28,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上. (1)已知:DE//AC,DF//BC. ①判断: 四边形DECF一定是什么形状? ②裁剪: 当AC=24cm,BC=20cm,∠ACB=45°时,请你探索:如何剪四边形DECF,能使它的面积最大,并证明你的结论. (2)折叠: 请你只用两次折叠,确定四边形的顶点D,E,C,F,使它恰好为菱形,并说明你的折法和理由. 六、统计与概率 43.如图29是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界 值,不含后一个边界值),则捐款人数最多的一组是(). A.5-10元 B.10-15元 C.15-20元 D.20-25元 44.以下问题,不适合用全面调查的是(). A.旅客上飞机前的安检 B.学校招聘教师,对应聘人员的面试 C.了解全校学生的课外读书时间 D.了解一批灯泡的使用寿命 45.为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,表1是这10户居民2015年4月份用电量的调查结果, 那么关于这10户居民月用电量(单位:度),下列说法错误的是(). A.中位数是55 B.众数是60 C.平均数是54 D.方差是29 46.已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为,则a等于 . 47.从一副扑克牌中选取红桃10.方块10.梅花5.黑桃8四张扑克牌,洗匀后正面朝下放在桌子上,甲先从中任意抽取一张后,乙再从剩余的三张扑克牌中任意抽取一张,则甲乙两人抽取的扑克牌的点数都是10的概率是____ 48. 2015年3月,某市某中学举行了“中国梦·校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图,如图30. 根据图中提供的信息,回答下列问题: (1)参加演讲比赛的学生共有____人,并把条形图补充完整. (2)扇形统计图中,m=____,n=____;C等级对应扇形的圆心角为 ____度. (3)学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求获A等级的小明参加市比赛的概率. 49.某数学兴趣小组对线段上的动点问题进行探究,已知AB=8. 问题思考: 如图31,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC .BPEF (1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值. (2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由. 问题拓展: (3)如图32,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点p从点A出发,沿A一B一C—D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点0所经过的路径的长. (4)如图33,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD .EF的中点,请直接写出点P从M到N的运动过程中,GH的中点0所经过的路径的长及OM+OB的最小值. 50.在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(-l,-1),(0,0),…都是“梦之点”,显然,这样的“梦之点”有无数个. (1)若点P(2,m)是反比例函数(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式: (2)函数y=3kx+s-l(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由: (3)若二次函数(a,b是常数,a>0)的图象上存在两个不同的“梦之点”,且满足,试求出t的取值。

