基于预习的“问题诱导”教学

过晓伟

培养思维能力是由“问题”开始的，又是在问题解决中发展的，这也是学好数学的前提。学生在课前预习中产生的疑问往往是其与新知对话的结果，它实际上可以为学生走进课堂提供良好的学习准备，基于预习状态下的“问题诱导”教学，抓住学生在预习中产生的问题进行设计，并通过和谐的互动诱发学生持续思考，促使他们去发现新知、探索新知，进而提高数学思维能力。下面笔者以苏教版三年级上册“两、三位数除以一位数”的教学为例，来谈一些具体的做法和思考。

一、汇聚“预习疑问”，设计“核心问题”，明确学习方向

学生通过预习，会在疑难处和新旧知识点链接矛盾的地方产生问题，如每个同学提一个问题，全班就会汇聚一串问题，这些问题有的细小、零碎，有的笼统，也有的具有思考性、启发性。这些问题来自于学生认知上的不同理解，课上一一解答显然效率低下，而且重点不突出。由此课堂上应对问题加以甄别，进行分类整合，进而形成直指本质、涵盖教学重难点、具有高水平的、以探究为主的“核心问题”，这样，这些具有思考性、探究性的问题就能让学生迅速明确学习目标，为学习思考指明方向。

例如，在教学苏教版三年级上册“两、三位数除以一位数”时，笔者对学生的问题作了如下整理：

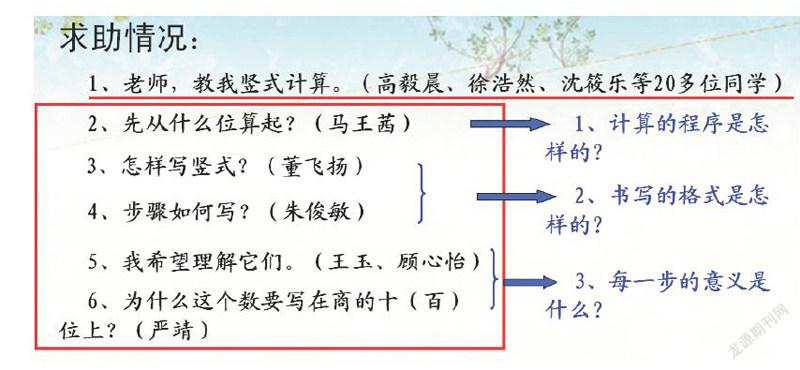
学生的问题一般具有共性，第一个问题有多位学生提出，其实是一个学习需求的集中求助，其他几个提问则目的性非常强，但在教学中不可能分裂开来解决，于是笔者把它们进行分类整合，归纳成三个学习的“重点问题”，以这三个“研究问题”贯穿全课。这三个问题其实就是新课内容的核心，抓住这三个问题，学生也就明确了新知的重点，解决了难点。因此，课堂上把学生的疑问采用化繁为简的策略进行归纳整理，变“问题串”为“大问题”，变“多环节”为“大板块”，改变原先教师一步一台阶、降低思维难度的一串串小问题的“点状思维”教学方式，让学生自主探究“核心问题”，这样充分凸显了以学生为主体的学习方式，也给学生创设更多时空去探索、去思考，有利于培养良好的思维品质。

二、基于“初步认识”，设计“启发性问题”，启迪积极思维

通过预习，学生对新知会有一定的认识，但在知识重构中会出现模糊、混淆、不全面、不规范的现象。在教学实践中，教师不能代替学生学习，不能简单地教给学生一个结论，而在于引导学生通过自己的思维活动掌握获取知识的过程和方法。因此，教师要根据新旧知识的内在联系，精心设计“启发性”的问题，启发学生通过自己的积极思维主动地寻找答案。

例如，在教学苏教版三年级上册“两、三位数除以一位数”时，笔者出示以下情境图：

学生列式后，设计了如下问题：“你想怎么算呢？能用画图、文字或算式说明吗？”

学生通过自主思考，呈现了如下多样算法：

上面通过“你想怎么算”这个综合性的问题，让学生自主思考“分”与“算”的过程。由于学生会分而不会算，所以学生就根据“问题”中的提醒“可以通过……”来解决“46÷2=”的问题，以上算法虽然只展现了分的过程，但其实已经展现了学生由“图—文字—式”思维的数学化过程。随后，笔者又提出以下几个问题：“这么多的分法其实都是先分什么，再分什么？”“都是先算什么，再算什么？”“哪种方法你觉得既简洁又包含了全部分的过程，为什么？”这些带有“启发性”的问题让学生对众多分法有了更深入的了解，对竖式计算的算理有了新的认识，为竖式计算的学习做好了准备。以上的教学展示、分享环节，不是简单的“说一说，看一看”，而是在学生展示自己原始思维的同时，通过阐述、分析、比较、筛选等智力活动，围绕多种原始思维展开的深度对话，完善和提高了个体认识。

所以，课堂中教师要在“关键处”善于设计启发学生思考的问题，准确把握学习的方向，让学生在初步认识的基础上得到充分交流经验、探讨、剖析的机会，让学习不断深入。

三、依据“学习经验”，引领“关键问题”，拓展思维深度

数学知识比较抽象，要让学生真正理解和自觉掌握数学基础知识并形成能力，关键在于对所学内容的深度理解。学生通过预习，对所学内容会有一定的了解，但在“关键问题”上还需要教师的引领，所以教师要尽可能地利用有限的时间，通过对“关键问题”进行广泛、深入的剖析，由浅入深，使学生对教学内容达到深度的理解。

例如，教学苏教版三年级上册“两、三位数除以一位数”时，笔者设计了如下一些问题：

以上的教学通过不断地追问，不仅让学生懂得如何计算，而且是对每一步、每一个数都进行了辨析，明晰了算法，理解了算理。在此基础上，笔者继续深入，又提出：“除法竖式与以往的其他竖式有什么不同点？”让学生对比不同的竖式，最后归纳总结出：

1.其他竖式都是把要计算的数上下对齐排列，除法竖式是把除数和被除数写在同一行。

2.其他竖式都是把要计算的数写在上面，结果写在下面，除法竖式是把结果写在最上面。

3.其他竖式都是从右向左计算，即按照个位数、百位数、千位数等由小算到大，除法竖式却是由最高位算起。

通过对以上“关键问题”的积极讨论和充分说理，学生对除法竖式有了更深刻的理解，不仅从模仿或单纯的计算中解脱出来，而且学生的思考得到了检查、强化、验证，零散的思考变得系统化、结构化，停留在表面的思考通过解释说明、质疑问难得到了深化，学习逐步走向深入，“数学理解”思想得到体现。

基于预习状态下的“问题诱导”教学在于要关注学生的已有认知水平和学习经验，充分尊重学生的原创思维，在汇聚众多疑问的基础上的“重要问题”“核心问题”“关键问题”是学生学习的关键，课堂上以“问题导思”为目标，为学生创设了更多的时空，让他们有时间和空间去自主探索、动手实践，这样，学生的思维会更主动、更灵活、更广阔、更深刻，学生的良好思维品质也得到了培养。

（江苏省无锡市云林实验小学 214101）