概率,了解不确定性
方弦
“概率”这两个字,除了出现在高中数学课本中外,最常出现的地方也许就是天气预报中的“降水概率”了,也就是未来几天下雨的可能性有多大。在数学领域中,概率论是专门研究“可能性”的一个分支。它涉及的问题非常广泛,涵盖的内容远远超过了课本里那些刻板的习题。

一切随机或者不确定的事件,都是概率论研究的范畴。上至气象下至金融,甚至连“磁铁的磁性是怎么来的”这种物理问题,都可以用概率的方法进行研究。
不过,虽然概率论的应用范围非常广泛,但这门学科的诞生却有些“不太光彩”。
来自赌博的问题
1654年的一天早上,法国数学家布莱兹·帕斯卡(Blaise Pascal)收到了他的朋友贡博的一封来信。这位朋友自称“来自梅雷的骑士”,也算是一位业余数学家。他向帕斯卡提出了如下问题:两位贵族A与B正在进行一场赌局,赌注是每人500法郎。游戏规则很简单,两人轮流掷硬币,得到正面则A得一分,反面则B得一分,每局两人得分的机会相等,谁先得到6分谁就拿走这1000法郎。两人激战至2比4之际,B突然有事需要提前中止赌局。那么问题来了,究竟应该如何分配赌资才最公平呢?

在数学中,这一类问题被称为点数分配问题。早在16世纪就有人研究过,不过当时数学家给出的答案并不令人满意,在某些极端情况下,甚至会给出非常不合理的分配方案。也许这位“梅雷骑士”正是见识过现实中因这类赌局和突发状况而引起的矛盾,因此才特意写信给帕斯卡,希望他能够完美地解决这个问题。
作为一代数学大家,帕斯卡对此也产生了浓厚的兴趣。随即,他便向另一位业余数学家皮埃尔·德·费马(Pierre Fermat)发去了一封信,共同讨论这个问题。“业余数学家之王”费马很快就给出了一个答案。他认为,不能单凭赌局停止时的比分或者各自获胜所需要的分数来决定赌注的分配,而是应该考虑所有比赛可能出现的状况,从而计算出双方的获胜比例。当然,列举所有可能性的计算量非常大,于是帕斯卡提出了一个简化算法,并完美地解决了点数分配问题。
实际上,他们的解答就相当于在计算两位玩家胜利概率的大小。在研究中,帕斯卡提出了“数学期望”的概念,以及著名的“帕斯卡三角形”(我国称其为“杨辉三角形”,即二项式展开式的系数规律)。某个结果为实数的随机事件的数学期望,也就是所有结果按照发生概率加权之后的平均值。
数学期望这个概念,掀开了概率论研究的序幕。无疑,帕斯卡和费马对早期概率论的发展起到了极大的影响。
什么是概率
很多概率问题都有着特别的结构。以某个非常简单的随机事件来说,比如抛掷硬币。我们知道每种结果出现的可能性的大小,而这类事件就被称为“基本事件”。我们可以多次重复这些基本事件,假定它们发生的可能性不会改变,而且这些重复没有相互影响。如果我们将这些基本事件以合适的形式组合起来,就能得到一个更为复杂而有趣的系统。
事实上,许多概率问题就是对这些随机系统的各种性质的研究。比如说,在点数分配问题中,基本事件就是硬币的抛掷,而系统则是赌局的具体规则,最后我们希望得知的则是每一方获胜的可能性大小。
在概率论的早期发展过程中,数学家研究的问题大多比较简单,不仅基本事件只有有限的几种结果,就连组合的方式也相对单一。这样构成的随机系统就被称为古典概型。
随着数学的发展,数学家开始考虑更加复杂的模型。18世纪,法国数学家布丰(Der Buffon)提出了这样一个问题:在数条间隔相等的平行线之间,随机投下长度与间距相等的一根针,那么它与这些平行线相交的概率是多少?在这个问题里,由于角度与距离都是连续的值,因此这样的基本事件就有着无数种不同的结果。这样的随机系统就被称为几何概型。
其实早在19世纪,概率论就已经成为了一门枝繁叶茂的数学分支。但有趣的是,直到20世纪,“概率”这个概念才有了严格定义。虽然古典概型的结果数量有限,其定义相对简单,并没有什么含糊之处,但几何概型的情况显然更为复杂。
我们不妨考虑这样一个问题:圆中有一条随机的弦,它的长度比圆内接正三角形的边长更长的概率是多少?其实,这个问题又叫做贝特朗悖论,它的奇特之处在于,选取“随机的弦”的方法不同,得到的概率也不尽相同。
直到1933年,俄国数学家柯尔莫哥洛夫(Andrey Nikolaevich Kolmogorov)为概率论建立公理体系之后,这个问题的解答才变得昭然若揭。柯尔莫哥洛夫将概率模型建立在某一类所谓的“σ代数上的测度”上,这样的测度可以有很多种,而不同的测度则对应着不同的“随机”。在贝特朗悖论中,选取随机弦的方法实际上对应着不同测度的选取,也就是不同的“随机”概念,自然会得到不同的结果。
如今,概率模型的种类已经变得越来越多,也越来越复杂,系统可以包含无限个基本事件,而具体的组织方式也更加繁复、更为有趣——随机图、渗流模型、自回避行走……这些概率模型早已不能用古典概型或几何概型来概括了。不过,也正是因为有了这些复杂的模型,我们才能用概率论解决在现实世界中碰到的种种难题。
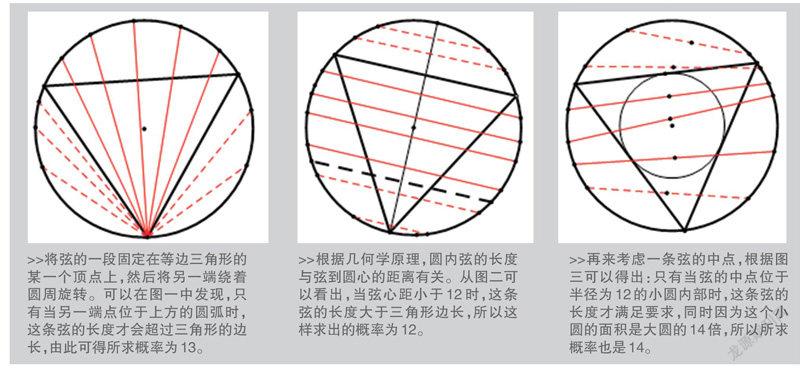
>>将弦的一段固定在等边三角形的某一个顶点上,然后将另一端绕着圆周旋转。可以在图一中发现,只有当另一端点位于上方的圆弧时,这条弦的长度才会超过三角形的边长,由此可得所求概率为13。
>>根据几何学原理,圆内弦的长度与弦到圆心的距离有关。从图二可以看出,当弦心距小于12时,这条弦的长度大于三角形边长,所以这样求出的概率为12。
>>再来考虑一条弦的中点,根据图三可以得出:只有当弦的中点位于半径为12的小圆内部时,这条弦的长度才满足要求,同时因为这个小圆的面积是大圆的14倍,所以所求概率也是14。
无处不在的分布
如果让数学家评选概率论中最重要的定理,桂冠可能非中心极限定理(Central Limit Theorem)莫属。它不仅是概率论中许多重要结果的基石,就是在其他学科,尤其是计算机科学领域,它也有相当重要的应用。而在现实生活中,它还是整整一个行业赖以生存的理论基础。
其实,中心极限定理不止一个,它的本质是一连串定理的总称,我们可以把它视为“大数定理”的细化与推广。

假设我们有一枚硬币,它掷出正反面的概率相等,那么,如果我们连续抛掷这枚硬币一万次,常识告诉我们,其中为正面的结果大概是五千次。这就是大数定理:如果对某个基本事件独立地重复多次,那么某个可能性发生的次数占总数的比例就会趋近于这个可能性发生的概率。
与大数定理不同的是,中心极限定理处理的则是那些结果是实数的随机基本事件。它告诉我们,如果将许多相同而又独立的基本事件的结果取平均值的话,那么这个平均值会趋向某个概率分布。如果根据大数定理,这个分布的数学期望就是基本事件的数学期望。而中心极限定理则告诉了我们额外的一点——这个概率分布必定是一个所谓的“正态分布”(Normal distribution),而它的方差,也就是概率分布的“分散”程度,是基本事件的方差除以事件数目的平方根。也就是说,基本事件越多,平均值的不确定性就越小。
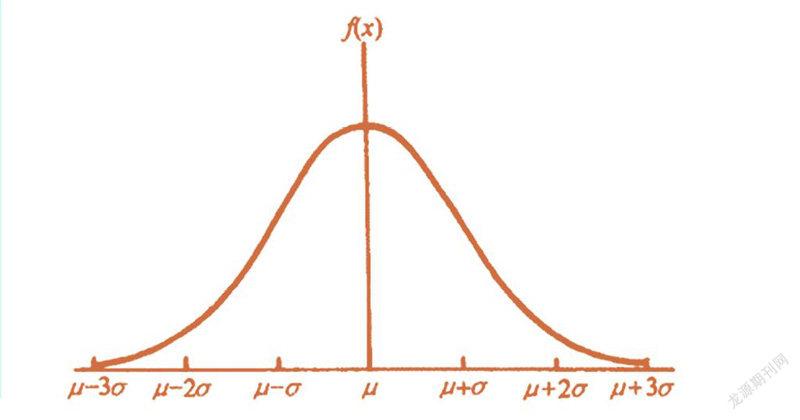
如果我们将这个正态分布画成曲线的话,那么它就像是一口大钟,中间高,两端则呈指数衰减,这也为它赢得了“钟形曲线”这么一个形象的名字。其实,中心极限定理可以推广到取值范围是高维空间中任意一点的情况,而“相同的基本事件”这个要求也可以被不那么严苛的条件代替——这些基本事件只要满足某些要求即可,不需要完全相同。
正态分布在自然界中随处可见,比如说人的身高和智力就服从正态分布。这是因为自然界中的很多现象,都是由各种因素相互交织而成的,其中并没有什么特别突出的因素。我们以人的身高为例,除了由许多不同的基因调控外,后天的营养、环境、健康,甚至是偶然的意外,都对身高有着各自的影响。在这种情况下,如果我们将每个因素都看成一个基本事件,并且假定这些因素各自的影响能力都差不多,那么将其综合考虑,根据中心极限定理,我们就会得到一个非常接近于正态分布的结果。
也许你很难想象,中心极限定理也是保险这一整个行业的基础。我们每个人都会遇到各种各样的风险,比如事故、疾病等等。虽然这些风险发生的概率都很低,可一旦发生,其后果将非常严重,并非每个人都能承受。而保险业实际上正是基于这一点,通过保费与保险赔付的方式,将上千万人连结了起来——每个人都只付出相对小的代价,但在不幸袭来时,就能获得一定的保障。根据中心极限定理,我们可以得知,由数量庞大的个案相加而成的保险业务,因偶然因素导致大额赔付的概率非常小,而且参与的人数越多,风险就越小。为了确定保费与赔付额,尽可能地获得盈利,保险公司实际上要做的就是根据大量的统计数据,精准地确定意外发生的概率,随后根据意外概率与收益,确定保费与赔付的金额。这也正是现代保险公司越来越重视概率与统计的原因。
理解复杂世界
除了与不确定性相关的问题之外,概率论与物理也有着千丝万缕的联系。法国物理学家皮埃尔·居里(Pierre Curie)在攻读博士学位时,就发现了一个关于磁铁的有趣性质:无论磁力多强的铁制磁铁,在将其加热到770℃时,都会突然失去磁性。这个温度后来就被称为铁的居里点。那么,为什么磁铁会突然失去磁性?通过概率论与统计物理分析,我们现在明白,这种现象与冰雪消融、开水沸腾类似,都属于相变的范畴。
我们可以将磁铁里的铁原子想象成一个又一个的小磁针,在磁铁还有磁性时,这些小磁针都会齐刷刷地指向同一个方向。但因为分子热运动的关系,每个小磁针都会时不时地动一下,但很快就会被附近的小磁针重新同化。物理学家将这个场景抽象成所谓的伊辛模型。通过对伊辛模型的研究,概率学家发现,当温度达到某个临界值时,整个体系就会由于热运动而不能保持统一的指向,这也意味着磁铁失去了磁性。这个临界值就是我们之前提到的居里点,而对伊辛模型的研究也部分揭示了磁铁一些微观结构的成因。

相变不仅仅局限于物理现象。流言的传播、传染病的爆发,还有微博的转发,都是一种相变过程,都存在着某种临界值。例如在“三人成虎”这个成语中,“三”就是所谓的临界值。又比如说传染病,在适当的模型下,如果每个病人传染人数的平均值低于某个临界值时,那么疾病就能被控制;如果高于临界值,就很可能导致疫病的全面爆发。虽然对于疾病传播的研究,属于流行病学研究的范畴,但在概率论被引入流行病学研究之后,我们对如何防止与控制疫病爆发有了更深入的了解,这是能够挽救成千上万人性命的知识。
当然,概率论的应用远远不止这些。大至失事飞机搜救,小至垃圾邮件过滤,我们都能在其中找到概率论的身影。这个复杂的世界充满了不确定性,有些无伤大雅,有些却能致命。若要驾驭这些不确定性,就要先从了解它们开始,这就是概率论的意义。
概率论不能为我们带来一个没有风险的世界,但它却能教会我们如何与风险和平共处,虽然它带来的仅仅是一种关于不确定性的知识。
但知识,往往就是力量。

