一类二次曲面在正交变换作用下的几何解释
孙卫卫
(青岛理工大学琴岛学院)
1 二维空间中一类正交变换的几何意义
定理1 正交变换Y=PX相当于在平面直角坐标系中将以原点为起点的向量X沿逆时针方向旋转角度θ得到以原点为起点的向量Y,且‖X‖ =‖Y‖.
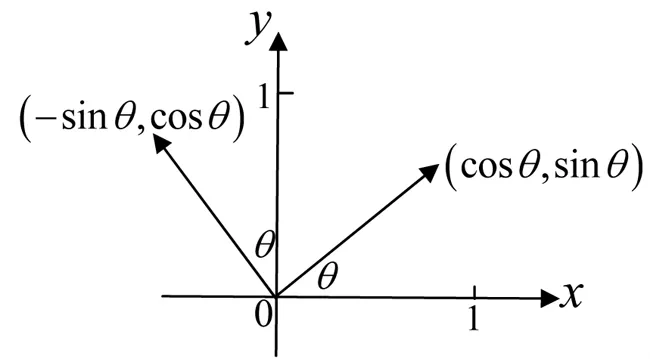
图1
例1xy=1是由什么样的二次曲线,并且从几何角度解释它是如何由标准的二次曲线旋转得到的.
2 三维空间中一类正交变换的几何意义
设正交矩阵P即向量X、Y为:

并给出正交变换Y=PX,则有如下定理.
定理2 正交变换Y=PX相当于在空间直角坐标系中保持与x轴夹角不变的情况下,从x轴正向看去,将以原点为起点的向量X沿逆时针方向旋转角度θ得到以原点为起点的向量Y,且‖X‖ =‖Y‖.
证明 由Y=PX知x1=x,故向量Y与x轴的夹角与向量X与x轴的夹角相同,对于向量X、Y其余的两个分量则有,故由定理1知Y=PX相当于在空间直角坐标系中保持与x轴夹角不变的情况下,从x轴正向看去,将以原点为起点的向量X沿逆时针方向旋转角度θ得到以原点为起点的向量Y,且‖X‖ =‖Y‖.证毕.
设正交矩阵:
在许沁这儿碰壁,并不感到意外,这事不经几个回合,是不会有结果的。雨落和玉敏在路上分析,若让许沁补款是勉为其难,可许沁为什么坚持不退货呢?是贪心所致,还是另有隐情?两人都说不清。雨落说许沁如果坚持说寄国外了,下次你让她出示邮局存根。
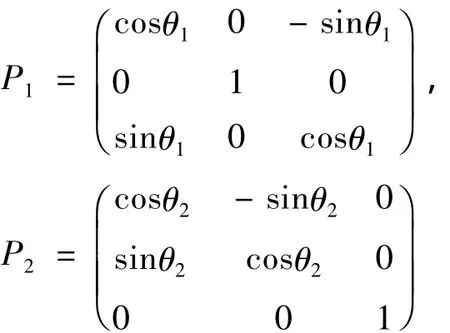
可以将此定理2的结论推广到如下的正交变换
Y=P1X与Y=P2X,可有如下结论:正交变换Y=P1X(Y=P2X)相当于在空间直角坐标系中保持与y(z)轴夹角不变的情况下,从y(z)轴正向看去,将以原点为起点的向量X沿逆时针方向旋转角度θ1(θ2)得到以原点为起点的向量Y,且‖X‖ =‖Y‖.
3 一类二次曲面在正交变换下的几何解释
给定二次曲面方程为:
设

方程(1)可等价为:

通过计算,A的特征值必有0,并设A的其他两个特征值为λ1、λ2,A为实对称矩阵,故必定存在正交矩阵P,有
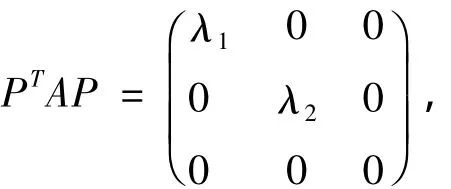
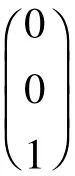
当A的特征值为0时,可得0的特征向量必定会有一个为,故此正交矩阵可写为以下形式:

令X=PY代入方程(2)中得:
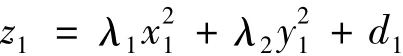

由定理2的结论可得如下定理.
定理3 方程(1)所表示的图形,可由方程(3)所表示的图形按照从z轴正向看去逆时针旋转角度α1而得到.也可将此结论推广到以下形式的二次曲面方程:

通过具体例题看定理3如何运用.
例2 分析下列方程分别表示什么样的二次曲面,并且从几何角度解释它是如何由标准的二次曲面旋转得到的:
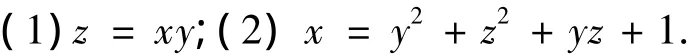
解 (1)z=xy,设:

则z=xy可写为z=XTAX,因为A为实对称矩阵,故存在正交矩阵P,有:

其中通过计算p可写为如下形式:

令X=PY,代入z=XTAX得到:
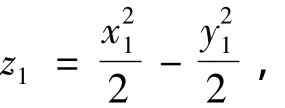
把下标去掉即有:

因此由定理3知z=xy为双曲抛物面,并且它是由双曲抛物面按照从z轴正向看去逆时针旋转角度45°而得.
(2)x=y2+z2+yz+1,设:
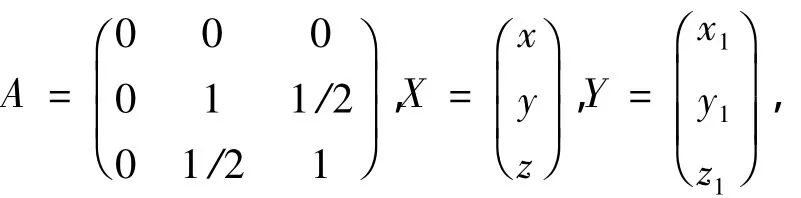
则x=y2+z2+yz+1可写为x=XTAX+1,因为A为实对称矩阵,故存在正交矩阵P,有:
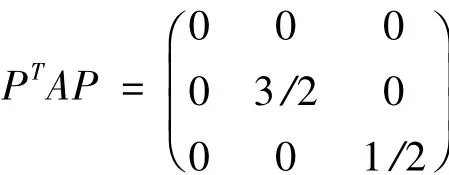
其中通过计算P可写为如下形式:
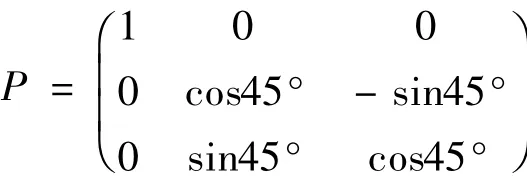
令X=PY,代入x=XTAX+1,得到:
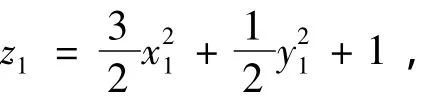
把下标去掉即有:

因此由定理3知x=y2+z2+yz+1为椭圆抛物面,并且它是由椭圆抛物面按照从x轴正向看去逆时针旋转角度45°而得.
[1]同济大学数学系.高等数学:下册[M].北京:高等教育出版社,2007.
[2]华东师范大学数学系.数学分析:下册[M].北京;高等教育出版社,2010.
[3]徐森林.数学分析:第三册[M].北京:清华大学出版社,2007.
[4]吴赣昌.线性代数:理工类[M].北京:中国人民大学出版社,2011.
[5]黄益生.高等代数[M].北京:清华大学出版社,2014.
[6]杨文茂.空间解析几何[M].武汉:武汉大学出版社,2004.

