非线性方程的周期积分边值问题分析

赵泽福

(昭通学院)

0 引言

Duffing方程的边值是解决跨共振和限制共振等问题的重要方法，随着研究的深入，从上个世纪30年代开始，Joseph Liouville和 Charles Srurm开始针对二阶常微分两点边值问题进行研究，并且将二阶线性微分方程表示为式(1)所示的形式:

其中，p(t)＞0，q(t)＞0，他们依据一系列研究成果最终形成了Srurm－Liouville理论.该文在此基础上对如下一般形式的二阶非线性微分方程进行研究.

其中，t∈［0，T］，p(t)∈C1(［0，T］，R)，并且f∈C1(［0，T］×R，R).

1 方程求解准备

1.1 假设条件

在该文的研究中，假设如下的条件成立:

(A1)存在常数a和b，对于所有的(t，x)∈［0，T］×R满足:

(A2)对于给定的常数M2＞M1＞0，满足M2≥p(t)≥M1.

(A3)存在N∈Z+，使得下式成立:

当p(t)=1时，方程(3)变换为

1.2 相关引理

在证明过程中，引入如下的标记:

γ={u(t)∈L2(0，T):u'(t)在［0，T］上绝对连续}

并且对γ空间的范数定义如下:

对γα，β线性子空间的定义如下:

γα，β={u(t)∈t:并且对于任意的［0，α］∪［β，T］满足u(t)=0}

其中:［α，β］⊂［0，T］，对于任意的u(t)和v(t)∈γα，β，令:

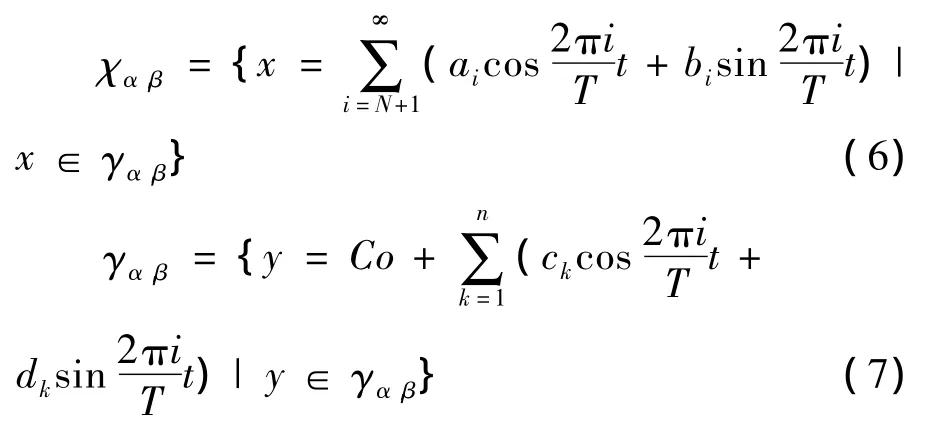
其中，a，b，c0，ck，dk为对应的傅里叶系数，因此根据如上的定义可以得到:γα，β=χα，β⊕γα，β.

并且，在空间γα，β中，定义实双线性型如下所示:

则对于u∈γα，β，如果有Hα，β(u，v)=0，则u≡0.

2 线性方程边值问题求解

其中，q(t)∈C(［0，T］，R).

证明1 假设(L1):存在常数a和b，使得对于所有的t∈［0，T］，有:a≤q(t)≤b.则当假设(A1)、(A3)和(L1)成立时，方程(10)只有零解

证明 假设方程(10)，根据假设克制，对于∀u∈γα，β，有:

因此，根据Parseval公式得到:

对于∀x∈χα，β，有

(1) 施做注浆锚杆：由于护盾上方坍塌体堆积，普通注浆锚杆施做比较困难，可采用3 m长Φ25自进式中空注浆锚杆，在护盾尾部斜向上前方布设；此外，由注浆模拟试验成果可知，浆液在以强蚀变围岩中的扩散半径为0.5 m～0.8 m，结合现场蚀变岩赋存环境，注浆锚杆的间排距取1.0 m。杆体上注浆孔孔径为6 mm～8 mm，孔间距40 cm，梅花型布设。

同理:对于∀y∈γα，β，有

假设v(t)是方程(10)的解，则vα，β(t)∈γα，β，对于∀u(t)∈γα，β，可得:

通过分部积分得到:

再根据公式(8)可知:对于t∈［0，T］，有vα，β≡0.即t∈［α，β］时，有v(t)≡0，得证.

证明2 当假设(A1)、(A3)和(L1)成立时，方程(9)只有零解

证明 利用反证法，假设当(A1)、(A3)和(L1)成立时，方程(9)有非零解x*，根据假设分成如下三种情况:

(1)如果x*(0)=x*(T)=0，则方程(9)变换为方程(10)的情形，通过如上的证明，方程(10)只有零解，与已知条件矛盾.

(2)x*(0)=x*(T)=η≻0

定义:S={t∈［0，T］:x*(t)=0}，a=，则根据

可知:在集合S中至少有两个零点，0＜a＜b＜T，且x*(a)=x*(b)=0.令:

方程(11)只有零解，从而得到t∈［a，b］，x*(t)≡0.由于0＜a＜b＜T，则对于t∈［0，a)∪(b，T］，有x*(t)＞0，从而得到:

(3)(p(t)x')'+q(t)x=η＜0，这种情况与第二种情况的证明类似.

综上，证明完毕.

证明3 假设方程满足(L1)、(A1)和(A3)的假设条件，而且h(t)，q(t)，p(t)连续，则方程(12)有唯一解.

证明 在空间γ中定义一个如下的线性子空间:

在线性子空间中，将方程(12)依据通论算法，转换为如下的等价问题:

根据μ的定义，以及假设(A1)成立，则在λ=0时，则前面的假设，方程(12)只有零解.因此，根据Leray－Schauder定理，对于所有的λ∈［0，1］，如果存在M0＞0，使得方程(12)的解满足:‖xλ(t)‖＜M0，则可以证明方程(12)有唯一解.如果不成立，那么存在‖xj‖⊂γ*，{λj}⊂［0，1］，当j→∞时，‖xj‖→∞ ，其中xj为λ=λj时，方程(12)的解.

根据Arzela－Ascoli定义，假设当j→∞时，λj→λ0，yj→y0，y'j→z0.并且，y0满足边值条件.当.从而得到:

与不存在非零解矛盾，证明方程(12)有非零解.

假设方程(12)有不止一个非零解，则令x1(t)和x2(t)是方程(12)的任意两个解，则令x(t)=x1(t)－x2(t).

根据假设(A2)可知:

然后利用前面证明2的结论，得到方程(12)解的唯一性，至此方程(12)解的存在性问题和唯一性问题得证.

3 结束语

微分方程的编制问题是微分方程理论的重要研究问题，并且在经济学、生物学、天文学、物理学等学科领域都有非常广泛的应用.一直以来，伯努利、欧拉、牛顿、拉格朗日等科学家都对微分方程的边值问题进行了大量的研究，并随着非线性分析理论的不断发展和完善，涌现了大量的新的研究成果.该文在前人研究的基础上，主要对二阶非线性方程的周期积分编制问题进行研究.

［1］Bashir Ahmad，Sivasundaram S.Existence of solutions for impulsive integral boundary value problems of fractional order［J］.Nonlinear Anal，2010，(4):4134–141.

［2］Benchohru M，Berhoun F，Nieto J，Nieto J.Existence results for impulsive boundary value problem with integral boundary conditions［J］.Dynamic Systems and Applications，2010(19):585－598.

［3］Li H，Liu Y.On sign－changing solutions for a second－order integral boundary value problems［J］.Comput Math Appl，2011，62:651–656.

［4］Li Y，Li Fuyi.Sign－changing solutions to second－order integral boundary value problems［J］.Nonlinear Analysis，2008，69:1179–1187