基于谐波平衡法的非线性低频隔振系统振动特性研究*

彭 超，程 林，王志海，吴文志，杨 静

(中国电子科技集团公司第三十八研究所， 安徽 合肥 230088)

基于谐波平衡法的非线性低频隔振系统振动特性研究*

彭 超，程 林，王志海，吴文志，杨 静

(中国电子科技集团公司第三十八研究所， 安徽 合肥 230088)

针对非线性低频隔振系统振动响应和振动传递率进行理论研究。基于非线性弹性元件的载荷-位移试验数据建立了非线性低频隔振系统的动力学模型和动力学方程。借助谐波平衡法对该非线性动力学方程进行近似求解，得到该非线性低频振动系统的一次谐波位移响应和振动传递率的近似表达式。分析了不同系统参数对振动传递率和曲线族骨架形状的影响，并对这种影响产生的原因进行了解释。理论结果与试验结果对比显示，当该非线性低频隔振系统工作在有效隔振频段内时，两者吻合良好。

非线性；低频隔振；谐波平衡法；振动传递率

引 言

传统的隔振系统能够很好地对中高频带进行隔离，但由于其在静承载力和低刚度之间的矛盾，很难适用于低频隔振。为了解决低频隔振问题，一些研究者将非线性弹性元件引入到隔振系统中，设计出一些非线性隔振系统。例如文献[1-2]将负刚度结构引入到隔振器的设计中，通过正负刚度并联的方式成功设计出了超低频的非线性低频隔振系统，表现出优良的低频隔振性能；文献[3-4]利用大变形弹性元件的几何非线性设计的非线性隔振器，在给定静载条件及变形量约束下可达到设定的动刚度值；另外摆式结构[5-7]、蝶形弹簧[8-9]、欧拉压杆[10-12]、片弹簧[13-14]等构件本身就可以实现高静刚度和低动刚度的非线性特性，都被引入到了低频隔振器的设计中。通过设计这些非线性隔振系统的参数，就可以使隔振系统能够在保持较大承载力的前提下具有较低的动态刚度，从而实现低频甚至超低频隔振。应用表明这类非线性低频被动隔振系统具有承载力高、起始隔振频率低的优点，且工作时几乎不需要消耗任何能量，是一种无源减振器件。也正是基于此，非线性隔振系统逐渐地被应用到实际的工程减振应用中。

由于非线性隔振理论还不完善以及非线性方程解的复杂性，长期以来都是将非线性系统简化为与之等价的线性系统进行分析和计算。然而采用线性理论来进行非线性系统的振动分析势必会造成较大的误差，对于强非线性系统，甚至产生错误，不能解释实际的非线性现象。非线性振动系统不像线性系统那样有统一的解析求解方法，常用的分析方法有几何方法、计算机仿真分析法和近似解析方法等。几何方法与仿真分析法均不能直接反应解与参数之间的直接关系。解析方法可以得到系统的响应幅值、频率和系统参数之间的闭合关系，以及响应对系统参数和初始条件的依赖关系。然而由于非线性解析方法的复杂性，系统的精确解通常无法获取，因此通常都是采用近似解析法来获取系统的近似解。近似解析法有正规摄动法、林滋泰德-庞加莱法、多尺度法、平均法、渐进法和谐波平衡法。其中谐波平衡法的概念和物理意义最为明确，实施操作最为简单，且适用范围不仅仅限于弱非线性系统，对强非线性系统同样适用，因而被大量地用来求解非线性系统的近似解。

文献[4]中针对低频隔振的需要设计出了一种非线性低频隔振系统，试验分析结果显示其具有明显的高静刚度和低动刚度特性，是一个典型的非线性隔振系统，是不能进行线性化的。本文将利用谐波平衡法对该非线性低频隔振系统的振动响应和振动传递率进行具体的分析。首先基于非线性弹性元件的试验数据建立隔振系统的非线性动力学模型。其次运用谐波平衡法对该非线性动力学模型求解；最后将理论结果和试验结果进行对比，以检验理论分析的正确性。

1 非线性低频隔振系统的动力学建模

图1 非线性低频隔振系统的力学模型

根据文献[4]中试验数据，将该非线性低频隔振系统弹性元件的恢复力fk在平衡点位置(工作点位置)拟合为位移的多项式。结合位移-载荷曲线的形状和弹性元件的实际物理意义，取位移的三次项和一次项，即该非线性系统弹性元件的恢复力-位移曲线(图2)可以表示为如下三次多项式：

fk=k1x+k3x3=11 378.6x+37 877 573.9x3

(1)

式中：k1为线性项系数；k3为非线性项系数。

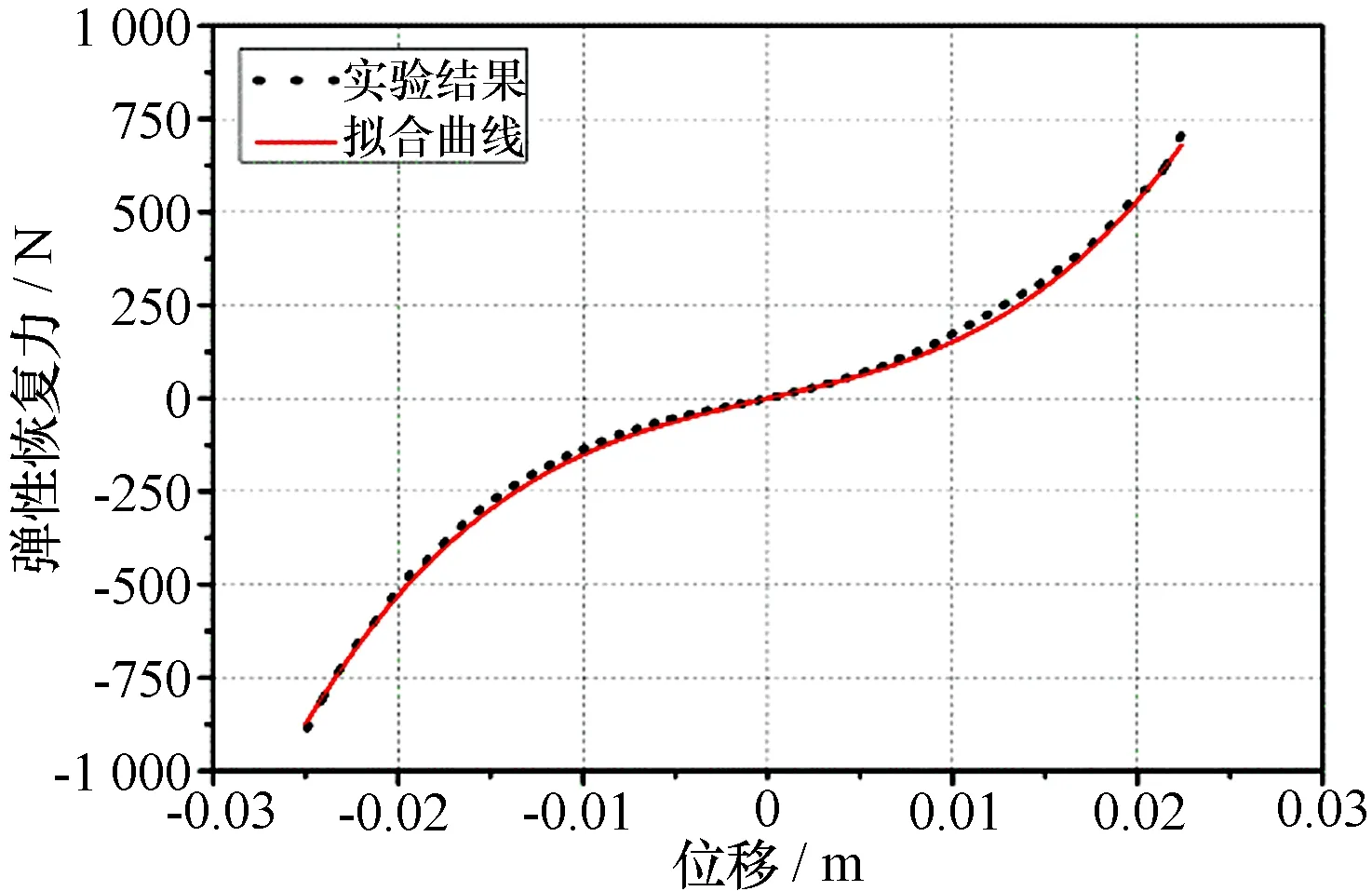
图2 恢复力-位移曲线

由图2可见，拟合后的曲线和实测数据非常接近，其精度完全满足工程应用需要。

在非线性低频隔振系统的实际应用中，引起阻尼的原因有很多。根据文献[4]中试验平台的实际情况，这里除了考虑系统的粘性阻尼外，还引入摩擦阻尼，其他类型的阻尼，例如结构阻尼等，都可以通过一定的形式转化为结构的粘性阻尼。粘性阻尼和摩擦阻尼都具有成熟的数学模型，可以表达为如下形式：

(2)

式中：fc为粘性阻尼力，与速度成正比；c为比例系数；fμ为摩擦阻尼力，为常数μFN，方向与相对运动方向相反；μ为摩擦系数；FN为摩擦接触面的正压力。

根据以上的分析和数学描述，该非线性低频隔振系统的动力学方程可以表示为如下形式：

(3)

(4)

式(3)为积极隔振模型的动力学方程；式(4)为消极隔振模型的动力学方程，可见这2个方程都是典型的二阶非线性非奇次微分方程。

对于上述二阶非线性非奇次微分方程，其解的表达式包含大量的非初等函数，很难获得精确的解析式。鉴于谐波平衡法适用范围广、物理意义明确和操作简单等优越性，采用谐波平衡法来对上述二阶非线性非奇次微分方程求解。谐波平衡法的基本思想为：将振动系统激励项和最终响应都展开为傅立叶级数，然后代入到振动系统的运动微分方程中，再令同阶谐波项的系数相等就能得到一系列的代数方程，通过代数方程就能确定傅立叶级数的系数，从而获得振动系统的解。其中令同阶谐波项系数相等的物理意义是保证系统的激励力和惯性力的各阶谐波分量能够自相平衡。

2 动力学方程求解

考虑到实际工程应用中针对基础振动进行的消极隔振的应用较为多见，且相对于式(3)，对式(4)求解要稍许复杂，因此这里以消极隔振模型的动力学方程式(4)为求解对象，采用谐波平衡法来获取其近似解析解。由式(4)可以将消极隔振模型的运动方程改写为由相对位移响应表示的形式：

(5)

式中，z=x-u即为非线性低频隔振系统的相对位移响应，即隔振对象相对基础的位移响应。

在实际工程应用中，很难直接采集基础的位移，或者采集的位移数据都不太准确，而测量基础的加速度相比而言要简单许多，例如大部分地震仪记录的都是地面的加速度响应，因此在消极隔振模型中，基础激励的输入条件一般都是以加速度的形式给出。为了与实际工程应用一致，直接假设基础简谐运动的加速度响应为：

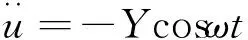
(6)

式中：Y为基础加速度幅值；ω为加速度。

将式(6)代入式(5)，就可以将式(5)改写为如下的形式：

(7)

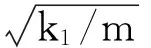
假设非线性低频隔振系统的一次谐波相对位移响应为：

z=Zcos(ωt-φ)

(8)

式中：Z为一次谐波相对位移响应的幅值；φ为一次谐波相对位移响应与基础激励之间的相位差。

为了得到Z和φ的表达式，将式(8)代入式(7)可得：

εZ3cos3(ωt-φ)]-2ξωω0Zsin(ωt-φ)-

(9)

式(9)中左端最后一项(摩擦阻尼项)展开成傅立叶级数有：

(10)

式中，an为傅立叶级数的各项系数。

将式(10)代入式(9)，化简过程中利用变换公式 4cos3α=(3cosα+cos3α)，最后得到

(11)

式中：Ω=ω/ω0为无量纲激励频率。

令式(11)中两端一次谐波项sinωt和cosωt的系数对应相等，得到：

(12)

将式(12)中两式平方相加消去φ得到：

(13)

式(13)即为非线性低频隔振系统的一次谐波位移响应的幅频特性表达式。进一步根据式(12)可以得到相频特性的表达式：

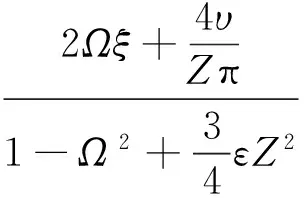
(14)

式(14)表示的是消极隔振模型中隔振对象相对于基础的相对位移响应，其与积极隔振模型的绝对位移响应具有相同的表达式。

将式(14)代入z=x-u可以得到消极隔振模型下非线性低频隔振系统的绝对位移响应为：

(15)

式中：

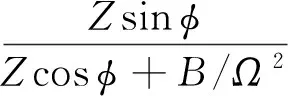
(16)

消极隔振模型下，系统的振动传递率定义为系统绝对位移响应和基础位移响应的幅值比，则由式(15)可以得到系统的位移传递率为：

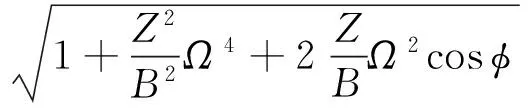
(17)

又由式(14)可得：

(18)

将式(18)代入式(17)并化简可得：

(19)

式(19)为根据动力学方程(4)求解获得的振动传递率，即为该非线性低频隔振系统在消极隔振模型下的位移传递率。同理求解动力学方程(3)将得到该非线性低频隔振系统在积极隔振模型下的力传递率，可得与式(19)完全相同的表达式。

3 系统参数对振动传递率的影响

根据上式可以得到非线性低频隔振系统在不同系统参数下的传递率曲线，如图3所示。

图3 系统参数对振动传递率的影响

图3(a)和(b)分别为不同粘性阻尼比ξ和摩擦阻尼比υ下的隔振系统传递率曲线。由图可见，随着激励频率的增大，传递率先增大后减小，当激励频率大于某一频率值时传递率小于1，该值即为隔振系统的起始隔振频率。在起始隔振频率的左右区间内，非线性低频隔振系统的ξ和υ对传递率曲线的影响与线性系统相似：在固有频率附近的共振区间内，阻尼比越小，振动传递率越大；在有效隔振区间内(传递率小于1的区间)，阻尼比越小，振动传递率越小，并且在此区间内υ比ξ对传递率的影响更为明显。但与线性系统不同的是，非线性低频隔振系统的无量纲起始隔振频率并不是固定不变的，而是随着阻尼比的变化而变化。这是因为阻尼比的变化会影响到系统的振动幅值，而非线性低频隔振系统的固有频率与系统振动幅值相关，进而就会影响到起始隔振频率。

图3(c)和(d)分别为基础激励系数B和非线性刚度系数ε对隔振系统传递率曲线的影响。由图可见，随着B和ε的增大，传递率峰值逐渐增大。随着激励频率的增大，传递率先增大后减小，最后趋于小于1的值。在有效隔振区间内，B对传递率的影响较为明显，并且B值越大，隔振效果越好。这说明在有效隔振区间内，当外界振动的频率成分相同时，振动量级越大减振效果越好，但是起始隔振频率也越大。在有效隔振区间内，ε对隔振频率的影响较小，随着激励频率的增大，不同ε的传递率逐渐趋于相等的值。由于ε和B的大小直接影响着系统固有频率的大小，因此起始隔振频率也随着参数的变化而变化。

由图可见，除图3(d)中ε=0外，所有传递率曲线都向着频率增大的方向倾斜，并且逐渐表现出多值特性，即在某一频率区间内同一频率对应的振动幅值有3个不同的值。当隔振系统工作在此频率区间内时，其幅值就会发生突变，这就是非线性系统特有的跳跃现象。对于隔振系统来说，这种跳跃现象会导致隔振对象产生较大的加速度，甚至造成系统的破坏，因此在非线性低频隔振系统的设计和实际使用中一定要避免这种跳跃现象的发生，例如设置合理的刚度系数、增加系统阻尼等。另外对比图中几组曲线族，图3(a)和(b)中，不管ξ和υ如何变化，曲线族的骨架不变。然而图3(c)和(d)中曲线骨架随着ε和B的增加逐渐倾斜，不稳定性逐渐增加。这是因为该曲线族骨架的形状与非线性低频隔振系统的无阻尼自由振动相关。令式(12)和式(19)中的阻尼系数和外激励力为0，就可以得到曲线骨架的表达式：

(20)

由式(20)可见，曲线族骨架的形状只与系统的ε和B的大小相关。其中ε=0时对应着线性系统，幅频特性曲线的骨架是一条垂直直线，且与横轴垂直相交于系统的固有频率处。

4 理论结果与试验结果对比

为了进一步检验理论分析结果的正确性，基于文献[4]中设计的非线性低频隔振系统和隔振试验平台，进行传递率的理论值和试验值的对比分析。隔振试验平台如图4所示。

图4 隔振性能试验评估系统[4]

该平台为一个两自由度系统，主要由基础质量块、载荷质量块、导杆、弹簧等构成。在基础质量块下面安装了激励器，通过激励器激励基础质量块来产生振动；激励器和基础质量块之间安装了阻抗头；在基础质量块和载荷质量块之间安装了非线性低频隔振系统的原理样机；基础质量块和载荷质量块在导杆的限制下只能在垂直方向上运动，并且分别在基础质量块和导杆、载荷质量块和导杆之间安装了直线轴承，以保证垂向运动的流畅性。

由于在简谐激励下，隔振对象的位移响应和基础位移响应的幅值比与两者的加速度幅值比相等。因此为了方便试验操作，在振动传递率的试验中直接采集载荷质量块和基础质量块的加速度响应，通过加速度响应的幅值比间接求出隔振系统的振动传递率。试验中频率为2 Hz～8 Hz，基础质量为120 kg，载荷质量为95kg。根据试验平台参数，设置计算参数ε=3300、ξ=0.08、υ=0.05，理论值与试验值的比较结果如图5所示。

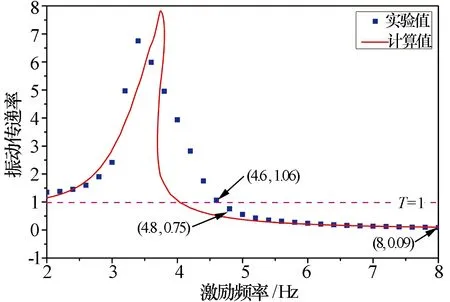
图5 理论计算结果与试验结果对比

由图5可见，试验结果和计算结果虽然在共振频率区间内有一定的偏差，但在有效隔振频段内，试验结果和理论计算结果吻合良好。鉴于隔振系统正常工作时都应该处于有效隔振区间内，因此计算结果和试验结果之间的这种偏差在工程上是可以被接受的。造成共振区间内偏差的原因主要有：

1)计算采用的方法为谐波平衡法，仅仅考虑了一次谐波的影响，本身就是一个近似计算过程；

2)计算中表现出的非线性的多值特性，是由于非线性低频隔振系统在共振区内的不稳定性引起的，这种不稳定性在试验中不能体现出来；

3)计算参数的选取、试验样机加工精度、测试系统的精度等等也会带入一定的误差。

5 结束语

在载荷-位移试验曲线的基础上，将非线性低频隔振系统弹性元件的刚度在平衡位置处拟合为位移的线性项和三次项之和，并且结合粘性阻尼和摩擦阻尼建立了非线性低频隔振系统的动力学模型和非线性动力学方程。

利用谐波平衡法对非线性动力学方程进行了近似的理论分析，得到该非线性低频隔振系统的一次谐波位移响应和振动传递率的近似表达式。考察了系统参数对振动传递率和曲线族骨架形状的影响，并且对此影响进行了解释。结果表明，阻尼系数对非线性低频隔振系统的传递率的影响与线性系统相似，但是与线性系统不同的是非线性低频隔振系统的振动传递率曲线随着系统参数的变化逐渐向频率增大的一方偏移，表现出多值特性，且系统的无量纲起始隔振频率随着系统参数的变化而变化；粘性阻尼比与摩擦阻尼比对曲线骨架没有影响，随着非线性刚度系数和基础激励系数变大，曲线骨架逐渐向频率较大的方向倾斜，系统不稳定性逐渐增加。

将理论结果与试验结果进行了对比，并分析了两者间略有偏差的原因。对比结果表明，虽然在共振频率区间内两者有一定的偏差，但是当该非线性低频隔振系统工作在有效隔振频段内时，理论结果和试验吻合良好。

[1] KOVACIC I, BRENNAN M J, WATERS T P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic[J]. Journal of Sound and Vibration, 2008, 315(3): 700-711.

[2] 张建卓, 董申, 李旦. 基于正负刚度并联的新型隔振系统研究[J]. 纳米技术与精密工程, 2004, 2(4): 314-318.

[3] VIRGIN L N, DAVIS R B. Vibration isolation using buckled struts[J]. Journal of Sound Vibration, 2003, 260(5): 965-973.

[4] 彭超, 龚兴龙, 宗路航, 等. 新型非线性低频被动隔振系统设计及实验研究[J]. 振动与冲击, 2013, 32(2): 6-11.

[5] FAN S, CAI Y, WU S, et al. Response of a folded pendulum to tilt tides[J]. Physics Letters A, 1999, 256(2): 132-140.

[6] LIU J, JU L, BLAIR D G. Vibration isolation performance of an ultra-low frequency folded pendulum resonator[J]. Physics Letters A, 1997, 228(4): 243-249.

[7] WINTERFLOOD J, LOSURDO G, BLAIR D G. Initial results from a long-period conical pendulum vibration isolator with application for gravitational wave detection[J]. Physics Letters A, 1999, 263(1): 9-14.

[8] HUNT J B, NISSEN J C. The broadband dynamic vibration absorber[J]. Journal of Sound and Vibration, 1982, 83(4): 573-578.

[9] LA ROSA G, MESSINA M, RISITANO A. Stiffness of variable thickness belleville springs[J]. Journal of Mechanical Design, 2001, 123(2): 294-299.

[10] WINTERFLOOD J, BLAIR D G, SLAGMOLEN B. High performance vibration isolation using springs in Euler column buckling mode[J]. Physics Letters A, 2002, 300(2): 122-130.

[11] DUMAS J C, LEE K T, WINTERFLOOD J, et al. Testing of a multi-stage low-frequency isolator using Euler spring and self-damped pendulums[J]. Classical and Quantum Gravity, 2004, 21(5): S965-S971.

[12] LEE C M, GOVERDOVSKIY V N, TEMNIKOV A I. Design of springs with “negative” stiffness to improve vehicle driver vibration isolation[J]. Journal of Sound and Vibration, 2007, 302(4): 865-874.

[13] BERTOLINI A, CELLA G, DESALVO R, et al. Seismic noise filters, vertical resonance frequency reduction with geometric anti-springs: a feasibility study[J]. Nuclear Instruments and Methods in Physics Research Section A, 1999, 435(3): 475-483.

[14] CELLA G, SANNIBALE V, DESALVO R, et al. Monolithic geometric anti-spring blades[J]. Nuclear Instruments and Methods in Physics Research Section A, 2005, 540(2): 502-519.

彭 超(1984-), 男, 博士, 工程师, 主要从事雷达结构设计、振动控制及力学仿真相关工作。

Vibration Characteristics Analysis of Nonlinear Low-frequency Vibration Isolation System Based on Harmonic Balance Method

PENG Chao，CHENG Lin，WANG Zhi-hai，WU Wen-zhi，YANG Jing

(The38thResearchInstituteofCETC,Hefei230088,China)

The theoretical research on the vibration response and vibration transmissibility of low-frequency nonlinear vibration isolation system is carried out in this paper. Based on the load-displacement experimental data of nonlinear elastic components, a dynamic model of low-frequency nonlinear vibration isolation system is developed and the nonlinear dynamic governing equations are proposed. The harmonic balance method is used to solve the nonlinear equations and approximate expressions of linear harmonic displacement response and vibration transmissibility of the vibration isolation system are derived. In addition, the effect of system parameters on the vibration transmissibility and the shape of curve family is studied, and the reason is interpreted. Comparison of theoretical results and experimental data shows that when the vibration isolation system works in low frequency range, they are well consistent.

nonlinear; low-frequency vibration isolation; harmonic balance method; vibration transmissibility

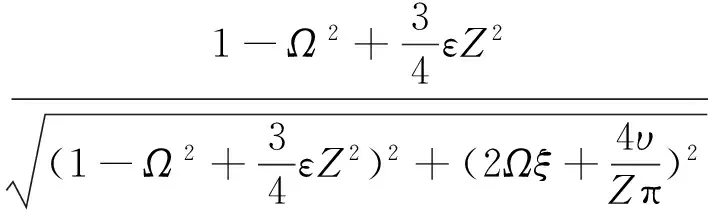
2015-01-05

O328

A

1008-5300(2015)03-0001-06