基于整车变形补偿的混凝土泵车臂架轨迹控制技术研究

赵 鑫，万 梁，王佳茜，化世阳（.湖南中联重科智能技术有限公司，湖南长沙4005；.国家混凝土机械工程技术研究中心，湖南长沙4005）

基于整车变形补偿的混凝土泵车臂架轨迹控制技术研究

赵 鑫1，万 梁2，王佳茜2，化世阳2
（1.湖南中联重科智能技术有限公司，湖南长沙410205；2.国家混凝土机械工程技术研究中心，湖南长沙410205）

为了使混凝土泵车工作装置实现良好的控制精度和操作平稳性，通过全姿态全工况下工作装置的变形分析，得出臂架和车身变形补偿模型，建立了变形补偿后的泵车工作装置运动学模型，并运用小脑模型神经网络（CMAC）+PID的控制方法解析动作控制量，很好地解决了臂架位姿动态检测和轨迹控制的问题.试验结果表明，该控制算法能满足轨迹控制的要求，使臂架末端位置动态检测误差控制在±8c m之内；借助变形补偿和臂架轨迹控制技术，臂架末端的运动轨迹误差可控制在±15c m之内.

工程机械；混凝土泵车；轨迹控制；变形补偿；小脑模型关节控制器（CMAC）算法

在现代化施工中，混凝土的大方量连续浇筑大部分采用泵送设备进行.混凝土泵车是一种用于输送和浇筑混凝土的专用机械设备，它可以将混凝土沿着输送管道连续泵送到浇筑现场，逐渐成为了建筑施工中不可或缺的关键设备［1］.

本研究以中联重科股份有限公司的某型号泵车为试验样机，阐明了泵车整车和臂架变形的特点，进行变形测量和补偿技术研究；对于泵车臂架末端工作轨迹动作进行算法研究，最后通过试验来验证变形补偿和臂架轨迹控制的正确性.通过泵车臂架轨迹控制技术研究，降低了操作手劳动强度，提高了泵车轨迹控制动作精度和操控性.

小脑模型关节控制器CMAC（cerebella modelarticulation controller）是由Albus在小脑时空模型Eccles的基础上于1975年提出的，仿照小脑如何控制肢体运动的原理而建立，是表达复杂非线性函数的查询自适应网络［2］.该算法神经网络比一般神经网络具有更好的非线性逼近能力，所以它在非线性函数逼近、动态系统建模等领域得到了广泛应用.Zhao等［3］在CMAC的基础上设计了一对机器人关节控制器，其中一个将CMAC与PID控制相结合，研究表明，基于CMAC+PID的控制器具有更好的稳定性.

1　泵车臂架运动学和变形补偿研究

1.1工作装置运动学分析

泵车臂架的工作机构是一个多自由度系统，由回转和多节臂组成.本文考虑6节臂泵车，即回转+6节臂组成的7个自由度系统.按选取变量不同，泵车工作机构可以分为3种空间表示法［4］：驱动结构空间［L0，L1，L2，L3，L4，L5，L6］、关节空间［θ0，θ1，θ2，θ3，θ4，θ5，θ6］和位姿空间［X，Y，Z］.工作装置末端的动作变化主要是通过臂架液压缸的伸缩变化来体现的，即正确控制液压缸的运动达到改变转角进而改变臂架末端的位置.本文以液压缸长度［L0，L1，L2，L3，L4，L5，L6］为控制变量，液压缸位移传感器实时反映液压缸长度变化并反馈给控制器，实时修正，从而使控制效果更加明显.

末端直线位移运动需分解为臂架平面的回转运动和各臂节在臂架平面内的运动.回转+6节臂逆求解规划为：

（1）建立以臂架根部铰点为原点、臂架运动之前的平面X-Y（为绝对平面，不随回转旋转）以及用右手法则确定的Z方向的坐标系.在X-Y-Z坐标系中，臂架末端从A点运动到B点，则已知坐标增量为（ΔX，ΔY，ΔZ）.

（2）已知坐标增量为（ΔX，ΔZ），则可通过三角形S AH反正切计算当前回转角度，减去上一次回转角度得到回转运动角度ΔA0.

（3）建立以臂架根部铰点为原点、臂架平面为R-H 平面的二维坐标系（注意此坐标平面将随着回转运动而旋转，因此与回转无关），通过已知坐标增量（ΔX，ΔY，ΔZ）求得规划后的R-H平面的末端坐标（R6（k），H6（k）），根据6节臂形成的矩阵方程反解求规划后的6节臂夹角角度.

（4）回转增量计算与6节臂角度增量是分开的，简化了计算难度.如图1所示.

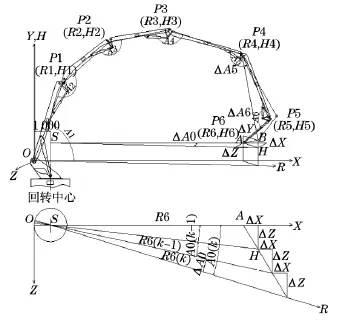
图1　回转和臂架装置分析简图Fig.1 Slew and booms equipment analysis

1.1.1回转规划角度计算

通过三角形S AH反正切计算当前回转角度A0（k）（即为臂架平面旋转的角度，顺时针旋转为正）.其中，每次启动时设定当前回转角度为相对0°.

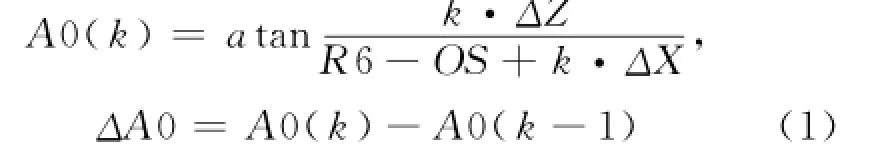
θ0=Δ A0为规划的回转角度，其中：OS为臂架铰点O与回转中心S的水平距离（试验样机的距离为1m）.

1.1.2臂架规划角度计算

泵车末端坐标系中的向量在其相对的基座标系中可表示为：

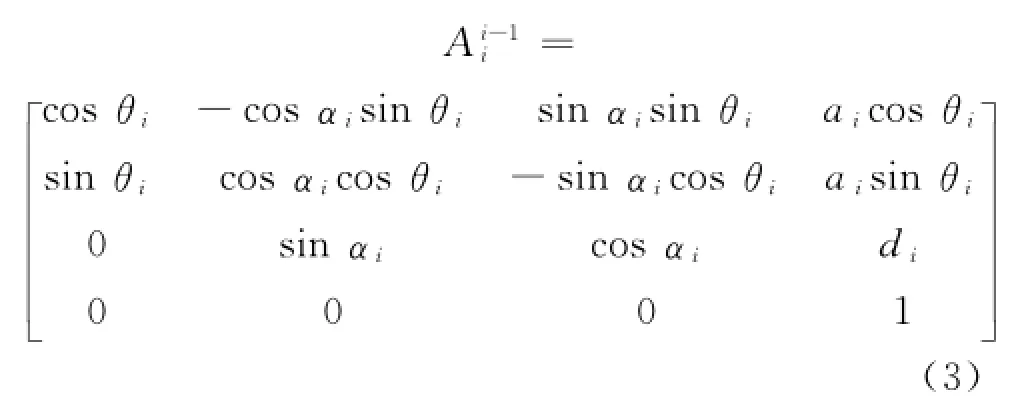
上式中：ai为臂架的长度；di为不同臂架在z方向上的偏移量，由于臂架结构在同一X OY平面内，所以di=0.不考虑泵车回转的情况下，即θ0=0，泵车臂架工作装置始终在同一平面内运动，则上式可简化为：

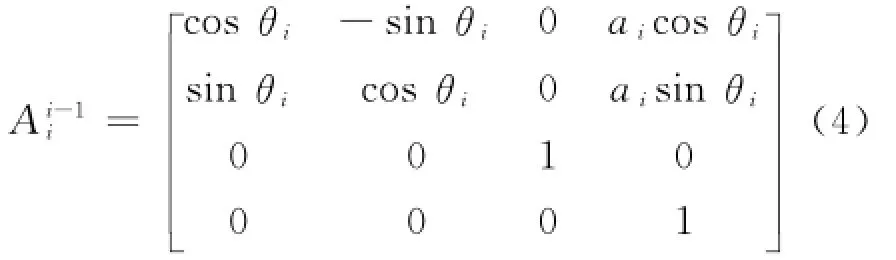
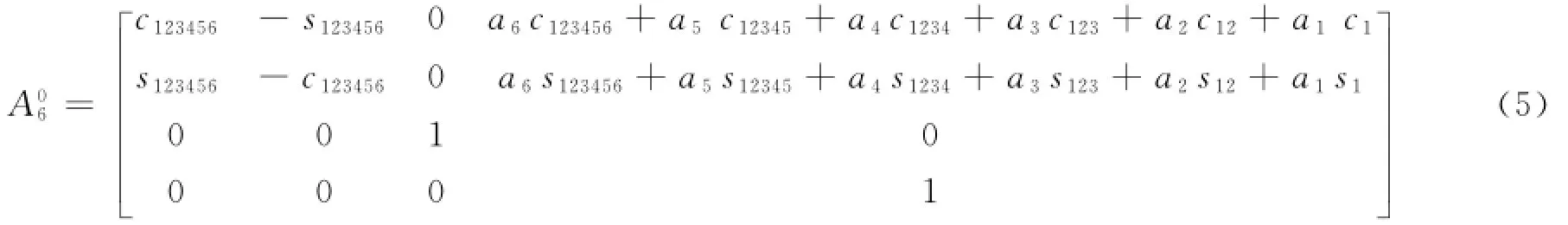
其中：si=sinθi，sij=sin（θi+θj），sijk=sin（θi+θj+θk），…；ci=cosθi，cij=cos（θi+θj），cijk=cos（θi+θj+θk），….

将臂架末端的位姿表示成向量［X，Y，Z］T的形式，则由式（5）可得下式：

通过式（6）可知，已知末端坐标（X，Y），可推导出各个臂架角度［θ1，θ2，θ3，θ4，θ5，θ6］.所以根据工作装置运动学模型得出规划的臂架角度为［θ0，θ1，θ2，θ3，θ4，θ5，θ6］.

1.2工作装置变形补偿分析

泵车臂架长度最长可达100m以上，由于长柔性臂架特有的结构，在其自身重力、负载剪切力、弯矩等因素的影响下受力复杂，会产生较大的弹性变形，且不同姿态下受力不同，变形的程度各异.在臂架运动过程中，回转和前几节臂架液压缸伸缩均会使整车重心和臂架重心发生较大范围的偏移，如图2所示.

姿态变形补偿控制方法.

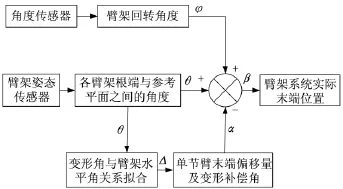
图3　臂架姿态变形补偿控制方法Fig.3 Deformation compensation control methodv

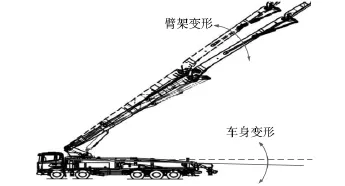
图2　泵车变形原理示意图Fig.2 TMCP deformation principle analysis

通过测试得出单节臂因为自身臂架变形而对末端测量高度误差的影响及其影响比重，其统计如图4所示.由图4可见，其中4臂的影响最大，其臂架变形会造成末端1500mm的测量高度误差，所占的影响比重为33%.采用臂架姿态传感器实时检测车身水平角度和臂架姿态变化，通过全工况仿真分析与加载试验，掌握臂架变形规律，建立车身、臂架姿态等参数与臂架变形的数学模型，在实际臂架运动控制中实时监测臂架姿态，并与臂架变形数学模型进行比对，通过线性小变形迭代运算，对臂架变形进行反向补偿，可以提高臂架运动动态精度.图3为臂架

2　轨迹控制的CMAC+PID算法

泵车臂架轨迹控制技术的原理为：将遥控器万向手柄给定的末端控制速度需求，通过一键操纵轨迹规划算法分解为多节臂的液压缸速度控制需求；通过阀控缸的速度闭环控制，实现精确的末端控制需求，如图5所示.为了很好地实现轨迹规划与控制，本文提出了小脑模型关节控制器（CMAC）+ PID控制算法.

2.1小脑模型关节控制器（CMAC）

CMAC网络是一种典型的局部逼近网络，具有A06=A01×A12×A23×A34×A45×A56，如果qn=［0，0，0，1］T，则q0为臂架末端在基座标系中的坐标，ai为各个臂架的长度，即ai=［L0，L1，L2，L3，L4，L5，L6］.

通过矩阵预算可以得出：

图4　单节臂变形对末端测量高度误差的影响Fig.4 Impact of different boom deformation to end trajectory error

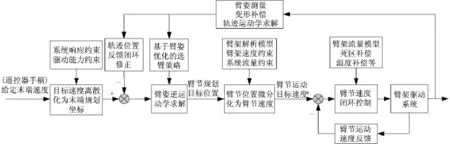
图5　轨迹控制框图Fig.5 Trajectory control diagram

线性结构，算法简单［5-6］，是一种模仿人类小脑的学习机构，图6为CMAC算法原理图.CMAC的工作原理可以描述为：CMAC接受一组输入变量，首先将其量化为一个离散的状态，并进而激活相对应的联想单元，所有被激活的联想单元根据其各自存储的联想强度进行加权求和来得到CMAC的输出，CMAC可以通过在线调整联想强度来逼近所要描述的函数关系［7］.试验样车的输入和输出量均和回转+6节臂动作相关，通过CMAC算法的控制，准确控制该动作的执行.

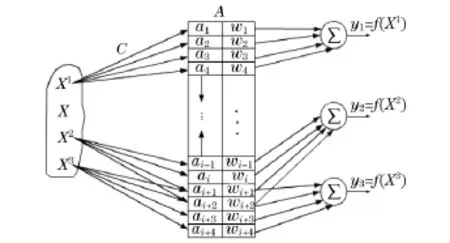
图6　CMAC网络示意图Fig.6 CMAC network diagram

2.2控制器设计

由式（6）可知，方程逆求解会有冗余解.为了得出最优变量条件，增加了臂架各个关节角度变化最小的约束条件.根据关节角度变化最小条件，得出最优的关节变化角度，规划出臂架运动的回转+6节臂动作.

图7为试验样本的系统控制器系统原理图，输入为液压缸的规划速度，输出为液压缸控制阀的输出电流值.

图7　基于CMAC的PID控制原理图Fig.7 PID control diagram based on CMAC该系统的控制算法为：

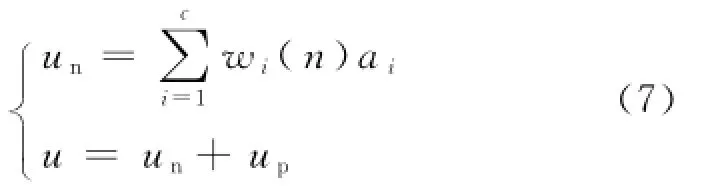
xi n（k）为输入信号，每一个控制周期结束后，总的控制输出u与C MA C输出un（n）作出比较，其差值为e，然后修正权值，进入学习阶段，主要目的是让e值最小，使系统总的控制输出由C MA C控制.

权值修正的方程为：

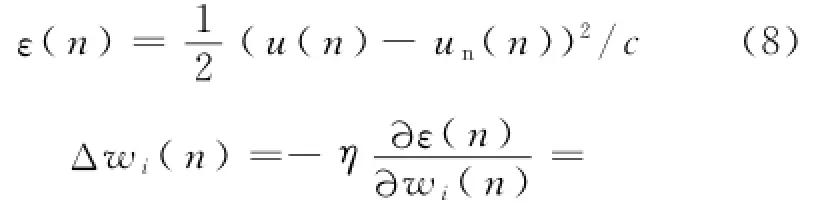
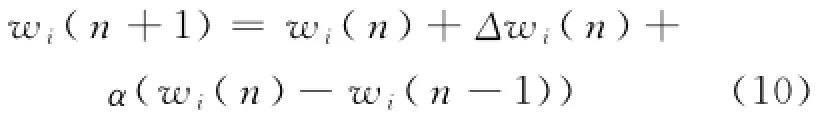
式中：η为学习率，η∈（0，1）；α为动量因子，α∈（0，1）.

通过CMAC算法的逐步学习，使CMAC产生的控制量un（n）逐渐逼近控制器的总输出u（n），PID控制产生的输出量up（n）逐渐为零.

3　试验研究

为验证泵车变形补偿及轨迹控制策略的正确性，以中联重科股份有限公司的某型号泵车进行试验验证.通过泵送混凝土工况下的工地试验，检测臂架变形补偿及轨迹控制精度.相关检测设备有位移传感器及末端激光测距仪等.

在泵送混凝土前，借助臂架变形规律模型，实时补偿因臂架和车身变形引起的臂架末端位置误差，使其动态误差控制在±8c m之内，如图8所示，使臂架的精确高效布料成为可能.

实际泵送混凝土工况下，借助变形补偿模型和臂架轨迹控制技术，臂架末端的运动轨迹误差可控制在±15c m之内，末端运动速度大于0.3m/s，如图9所示.显然，所得结果符合臂架运动精确控制精度要求，说明变形补偿及轨迹控制策略极大地提升了泵车臂架轨迹控制精度，提高了泵车控制的智能化水平和安全性，降低了操作手的操作难度.

图8　臂架末端检测误差Fig.8 Boom end detecting error

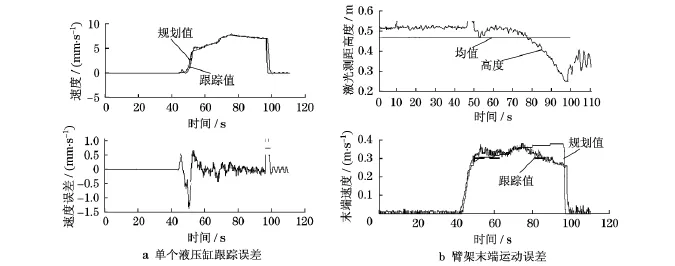
图9　跟踪误差Fig.9 Track error

4　结语

本文提出了对泵车车身和臂架变形的一种补偿方法，提高了臂架末端位置的检测精度；采用回转和臂架分离计算的新型运动学分析方法，简化了计算难度；针对臂架控制的CMAC+PID控制策略方法来实现对泵车臂架实时准确的控制.通过中联重科某款泵车试验验证，证明了变形补偿和CMAC +PID算法的正确性，臂架末端位置检测误差可控制在±8c m之内，臂架末端的运动轨迹误差可控制在±15c m之内.

［1］ 黄毅，吴斌兴，王佳茜，等.混凝土泵车臂架振动响应的主动控制实验研究［J］.振动与冲击.2012，31（2）：91-94.

HUANG Yi，WU Binxing，WANG Jiaqian，et al.Test for active control of boom vibration of a concrete pump truck［J］. Journal of Vibration and Shock，2012，31（2）：91-94..

［2］ 侯世英，时文飞，万江.基于CMAC-PID控制的柴油发电机组的建模与仿真［J］.系统仿真学报，2007，19（13）：3052-3063.

HOU Shiying，SHI Wenfei，WAN Jiang.Modeling and evaluating of diesel generators based on CMAC-PID［J］. Journal of System Simulation，2007，19（13）：3052-3063.

［3］ ZHAO H L，SUGISAKA M.Simulation study of CMAC control for the robot joint actuated by McKibben muscles［J］. Applied Mathematics and Computation，2008，203（1）：457

［4］ 周波，周辉.挖掘机器人工作轨迹跟踪智能控制［J］.武汉科技大学学报：自然科学版，2002，25（4）：402-405.

ZHOU Bo，ZHOU Hui.Intelligent control of trajectory tracking of a robotic excavator［J］.Journal of Wuhan University of Science and Technology：Natural Science，2002，25（4）：402-405.

［5］ALBUS J S.A new approch to manipulator control：The cerebella model articulation controller（CMAC）［J］.Journal of Dynamic Systems，Measurement，and Control，1975（9）：220-227.

［6］ 何剑春，王慧燕.CMAC网络建模在非线性预测控制中的应用［J］.控制与决策，2002，17（1）：92-95.

HE Jianchun，WANG Huiyan.Application of CMAC neural network to nonlinear predictive control［J］.Control and Decision，2002，17（1）：92-95.

［7］ 孙炜，王耀南.模糊CMAC及其在机器人轨迹跟踪控制中的应用［J］.控制理论与应用，2006，23（1）：38-43.

SUN Wei， WANG Yaonan.Fuzzy cerebellar model articulation controller and its application on robotic tracking control［J］.Control Theory & Applications，2006，23（1）：38-43.

Boom track control on concrete pump trucksbased on deformation compensation

ZHAO Xin1，WAN Liang2，WANG Jia-qian2，HUA Shi-yang2
（1.Hunan Zoomlion Intelligent Technology Co.，Ltd.，Changsha 410205，China；2.Chinese National Engineering Research Center of Concrete Machinery，Changsha 410205，China）

To guarantee high control precision and operational smoothness of concrete pump trucks，theworking device deformation is first analyzed under entire postures and conditions.Then，a boom and bodydeformation compensation model is obtained.By establishing the kinematical model of working device，themotional control quantity is analyzed via CMAC and PID techniques for dynamic boom posture detectionand track control.Finally，it is found from testing results that the proposed control algorithm can satisfytrack control，while the dynamic detection errors are controlled within ±8 cm regarding booom endpositions.Based on the deformation compensation and boom track control，the corresponding motion trackerrors can be controlled within±15 cm.

construction machinery；concrete pump truck；track control；deformation compensation；cerebella model articulation controller（CMAC）algorithm

T B 53

A

1672-5581（2015）06-0492-06

湖南省战略性新兴产业科技攻关项目资助（2013GK 4050）

赵 鑫（1985-），男，硕士.研究方向：工程机械机电液一体化.E-mail：yunruifeihua@163.cOm